python深度学习入门笔记全面总结！！（持续更新）

前言

之前有过断断续续地学习深度学习的经历
对深度学习有一定的了解
包括激活函数，损失函数，卷积，池化这种基本概念
对CNN，RNN，ResNet都有一定的了解
去年参加的项目里还和队友一起做了个基于CNN的智能搜索引擎
（没记错的话还花里胡哨地用了点jieba分词）
不过当时才刚刚大二，知识体系漏洞很大，项目全靠带
现在再翻翻当时的源码都得费好大劲才能回想起来在写什么。。。

而想想自己到底学了点什么深度学习，又很难系统地总结出来，东一榔头西一棒，确实很多片面的知识点都会些，但又不深入
所以以此契机我决定从头好好梳理一遍深度学习，从最基础的概念开始补全知识漏洞，同时呢就当是对相关的知识也做一个复习（比如线性代数，概率论，python之类的）

话不多说，希望能在新一遍的学习中有所收获吧——

神经网络基础

Logistic回归

Logistic回归主要是适用于分类问题的算法
毕竟是入门笔记，这里就只对二元分类做简述并给出概念定义

其基本的线性回归形式为：
$$y=w^{T}x+b$$
注：该子标题中的Logistic回归与上述表达式略有差异，具体可以参考子标题向量化
当然，用最基础的数学知识来看，这里的 y 取得的是一系列的实值
甚至在理论上值域为 R
而我们期望得到的值域为
$$[0,1]$$
即我们输入一个 x 后，我们需要知道一个概率区间
这就需要需要在外层嵌套函数，转变函数的值域
最理想的自然是单位阶跃函数，但单位阶跃函数一个缺点就是其不连续，不能保证可微的严格性，所以不能直接使用
所以这里需要对单位跃迁函数进行替换，
也就是sigmoid函数：
$$y=\frac{1}{1+e^{-x}}$$
也就是说最后可以表示为：
$$y=\sigma (w^{T}x+b)$$
其中
$$\sigma (x)=\frac{1}{1+e^{-x}}$$
此处我们定义：
$$y=P(y=1|x)$$
而当我们在进行神经网络训练时，此时产生的 y’ 只能说是理论值，为了使这个理论值 y’ 和实际值 y 接近，我们需要定义一个损失函数loss去衡量 y’ 和 y 之间的误差：
注：推导过程可以参考周志华教授的《机器学习》，这里只写结论
$$L(y,y)=-(ylogy+(1-y)log(1-y))$$
函数的前一个参数为理论值， 后一个参数为实际期望值
（实际上这就是一个经典的交叉熵损失函数）
也许有人会觉得为什么不用误差平方进行求值
但实际上，至少我所接触的神经网络都是利用梯度下降法进行训练的
而在梯度下降的过程中会面临很多凸函数问题
到那时你就会发现误差平方并不精确，不能有效地找到局部最小值
所以综上，我们选择上述功能相近的loss函数作为替换
再回看loss函数：
$$L(y,y)=-(ylogy+(1-y)log(1-y))$$
这里并没有标明log的底数（并不是默认为10），而实际上 log 的底数并不影响函数的实际含义：
我们使用loss函数的目的是为了衡量理论值和实际值的误差
所以对上述函数进行分析
你会发现当理论值 y = 1 时， y’ 也需要趋于1，反之理论值 y = 0 时 y’ 趋于0亦成立，从而确保了理论值和实际期望值最大程度上的吻合

明确了loss之后，我们还需明确另一个概念cost
loss是神经网络在单个训练集上的表现
cost则是神经网络在整个训练集上的表现
若训练集为：
$$\left\{(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),...,(x^{(m)},y^{(m)})\right\}$$
则cost为：
$$J(w,b)=\frac{1}{m}\sum _{i=1}^{m}L(y^{(i)},y^{(i)})$$
w 和 b 就是Logistic回归中的参数，在实际训练中应该是作为超参处理的

梯度下降法

在上个子标题中我简单梳理了Logistic回归以及 loss 和 cost
那么在已知cost表达式的情况下，我们对初次训练的神经网络进行参数 w 和 b 的设定，显然，除非你运气够好，不然初次设定的参数一定是具有较大偏差的——
我们对 w ， b ， J(w, b) 建立空间坐标系，得到如下的空间曲线：
注：下图截取自吴恩达老师的深度学习课程

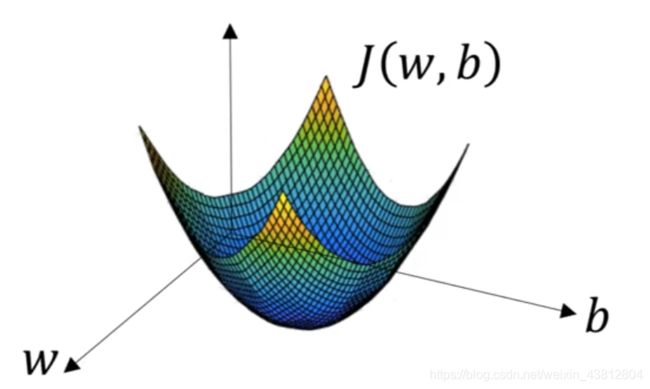
为了达到理论值和实际期望值最贴近的状态
我们需要 J(w, b) 取到局部最小值
而实际上对 w 和 b 的初次调参往往会有很大的误差
这时候我们就需要神经网络遵循一套规则渐进找到这个最低点
这里使用的就是梯度下降法

现在具体的解释梯度下降法的原理：
为了方便研究，我们先将上图的空间坐标系降维至平面坐标系
假定 b 是已知确定的
此时我们只需研究 w 和 J(w) 的图像：
注：下图截取自吴恩达老师的深度学习课程

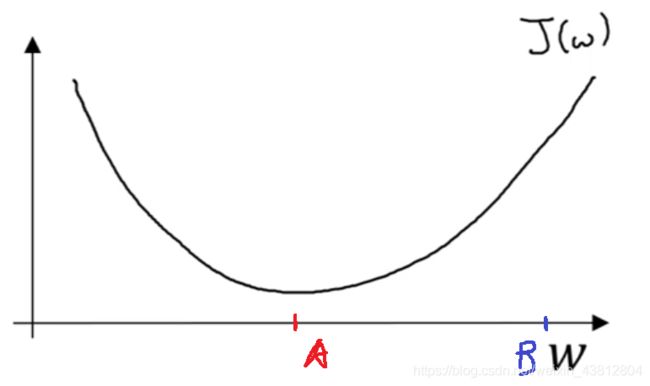
在原图的基础上我添加了红点和蓝点
分别对应局部最小值和初次调参值
为了使神经网络能渐进地从 B 过渡至 A ，我们对 w 进行以下修正：
$$w=w-\alpha \frac{dJ(w)}{dw}$$
这便是梯度下降法的核心思路
其中：
$$\frac{dJ(w)}{dw}$$
是函数在当前点的斜率，对应了梯度下降的方向
而参数 α 是学习率，对应了沿当前点的斜率方向下降的深度
参数 α 非常重要，其取值决定了梯度下降的效率：
太大则容易错失最低点
太小则下降速率过慢，降低了程序执行的速度

当你将 B 点选定在 A 点左侧时，再从公式上理解时：
你会发现横坐标在增加
但从函数趋势上是在下降的，仍然对应了梯度下降
清楚理解平面坐标系的情形后，我们重新回归空间坐标系
实际上空间坐标系和平面坐标系建立在完全一致的数学规则上
只是需要对 w 和 b 同时进行修正：
$$w=w-\alpha \frac{\partial J(w,b)}{\partial w}$$
$$b=b-\alpha \frac{\partial J(w,b)}{\partial b}$$

梯度下降法的具体运用

在分别介绍了 Logistic回归 和 梯度下降法 后
我们将两者结合起来审视，看看具体的运作机制
首先我们假设我们的训练集为：
$$T=\left\{(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),...,(x^{(m)},y^{(m)})\right\}$$
其中：
$$\left|T\right|=m$$
并假设在Logistic回归中，w 可表示为集合：
$$W=\left\{w_1,w_2,w_3,...,w_n\right\}$$
使得：
$$y=w_1{x}_1+w_2{x}_2+...+w_n{x}_n+b$$
我们将此结果赋值给变量 z 以方便后续的变量区分
$$z=y=w_1{x}_1+w_2{x}_2+...+w_n{x}_n+b$$
并在外层嵌套sigmoid函数，使得：
$$a=\sigma (z)$$
依照上文，这里的 a 就是理论值
我们再假设实际期望值为 y
进而求得：
$$L(a,y)=-(yloga+(1-y)log(1-a))$$
运算至此，我们已经求得了Loss函数，接下来，我们只需要反推：
$$\frac{\partial L(a,y)}{\partial w_j}$$
以获取梯度下降中的关键参数
其实对于有一定微积分基础的人而言，这个反推过程并不复杂
（其实就是反向传播）
只需要对链式规则加以利用即可：
$$\frac{\partial L(a,y)}{\partial w_j}=\frac{\partial L(a,y)}{\partial a}\times \frac{\partial a}{\partial z}\times \frac{\partial z}{\partial w_j}$$
省略具体的偏导过程，我们最终求出结果：
$$\frac{\partial L(a,y)}{\partial w_j}=x_j\times (a-y)$$
而实际上，在上一个标题中，梯度下降公式中对应的参数为：
$$\frac{\partial J(w,b)}{\partial w}$$
也就意味着我们需要对整个训练集进行处理，从而求出该参数，
定义额外变量如下：
$$J=0;w_1=0;w_2=0;...;w_n=0;b=0;$$
遍历整个训练集，有：
$$J+=L(a^{(i)},y^{(i)})$$
$$w_j+=x_j^{(i)}\times (a^{(i)}-y^{(i)})$$
$$b+=(a^{(i)}-y^{(i)})$$
并对整个训练集取平均：
$$J=\frac{J}{m}$$
对其余设定的额外变量做同样的取平均处理
由此我们可以求得：
$$w_j=\frac{\partial J}{\partial w_j}$$
同理：
$$b=\frac{\partial J}{\partial b}$$
并带入最终的梯度下降公式中
就可以对输入的各个参数作出一次修正了

向量化

神经网络的相关基础概念已经基本整理完毕
但是如果只按上述流程去编写机器学习算法
咳咳
那么你会发现整个程序的执行效率令人窒息

仔细分析上述流程
我们将发现设计的算法中将不可避免的有 for 循环
但在实际的机器学习过程中
显式的 for 循环会降低整个程序的执行效率
而实际上，真正在训练神经网络时训练集的容量是大到恐怖的
就拿我之前的做的搜索引擎举例
当时的训练集将近30G，涵盖了140w张图片
事实上神经网络会被投入比之更大的训练集，往往达到千万级甚至更大
（自己的笔记本默默无闻地跑了6个多小时才把训练集用掉。。。）

所以面对如此之大的训练集
即使是毫秒层面的时间效率都应该被予以重视

这里将使用向量化对上述正向传播的过程进行优化
这里我们假设对于每个训练集 x，都是一个 k 维的列向量（即 k 个特征）
那么对于整个训练集合 X ，我们可以设 X 为：
$$X=[x^{(1)},x^{(2)},x^{(3)},...,x^{(m)}]$$
不难发现这是一个 k * m 的矩阵
而对于 k 维向量中每个特征所对应的 w，我们设 W 的转置为：
（从实际意义出发 W 应该是一个列向量）
$$W^T=[w_1,w_2,w_3,...,w_k]$$
此时我们会发现，在之前的正向传播过程中，
循环中所有的 Z 亦可被构造为向量：
$$Z=W^{T}X+b$$
显然 Z 也是一个 m 维向量
在矩阵加减的逻辑上， b 也必须是一个 m 维向量
但得益于python的广播机制
实际编写过程中只需将 b 赋值为常规整型即可
对于反向传播也是同理，对于：
$$\frac{\partial L(a,y)}{\partial z}$$
我们亦可以构建 m 维向量，使得：
$$Z=[\frac{\partial L(a^{(1)},y^{(1)})}{\partial z^{(1)}},\frac{\partial L(a^{(2)},y^{(2)})}{\partial z^{(2)}},...,\frac{\partial L(a^{(m)},y^{(m)})}{\partial z^{(m)}}]=A-Y$$
其中：
$$Y=[y^{(1)},y^{(2)},y^{(3)},...,y^{(m)}]$$
$$A=\sigma (Z)$$
而对于最终所要求的：
$$w_j=\frac{\partial J}{\partial w_j}$$
$$b=\frac{\partial J}{\partial b}$$
我们只需依照原反向传播过程稍加变化即可：
$$B=\frac{1}{m}\sum Z$$
$$W=\frac{1}{m}X{Z}^T$$

至于为什么采用显示的 for 循环会导致效率变低
我所使用的课程资源中并没有给出详细解释
通过查阅资料，我给出一些个人理解：
首先：
事实如此，当向量维度为100w时，写个程序就会发现存在400ms+的时间差距
其次：
我们在编写上述流程的算法时，其实需要嵌套三层循环
而在数学本质上
我们也正是模拟了一个矩阵乘法的过程
无非没有定义相应的矩阵
而常规的矩阵乘法都是三层循环，时间复杂度为O(n^3)
但python中的numpy库给出的应该是优化过的矩阵乘法
目前最优的矩阵乘法是2014年由François Le Gall简化的斯坦福方法，时间复杂度为O(n^2.3728639)
个人认为使用显式 for 循环所产生的细微时间差正源于此

初识神经网络

神经网络中的Logistic回归

整理完最基础的知识点之后
我们将上述的知识点放入一个实实在在的神经网络里进行深入理解：
如下是一个简单的神经网络：

从左至右依次是输入层，隐藏层和输出层
但输入层往往也会被视为一层常规神经网络
所以我们通常将这类神经网络命名为双层神经网络

此时我们将从左至右的每一层依次标记为（如上图）：
$$a^{[1]},a^{[2]},a^{[3]}$$
依照上图的逻辑结构，我们在第 1 层神经网络（隐藏层）中
将会计算四次Logistic回归，从上至下依次为：
$$a_1^{[1]},a_2^{[1]},a_3^{[1]},a_4^{[1]}$$
而这些结果又将进一步被输出至输出层中
则在隐藏层中我们进行的计算可被表示为：
$$z_i^{[1]}=w_i^{[1]T}x+b_i^{[1]},a_i^{[1]}=\sigma (z_i^{[1]})$$
但仅仅这样依旧会产生显式for循环
接下来我们尝试对该流程向量化：
上述流程中我们会得到 4 个Logistic回归单元
每个单元都是一个3维列向量
我们将其堆叠起来，从而组成一个 4 * 3 的矩阵：
$$W^{[1]}=\left[\begin{array}{c}{w}_1^{[1]T}\\ w_2^{[1]T}\\ w_3^{[1]T}\\ w_4^{[1]T}\end{array}\right]$$
为验证其正确性，我们将该矩阵与：
$$x=\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]$$
相乘并与：
$$b^{[1]}=\left[\begin{array}{c}{b}_1^{[1]}\\ b_2^{[1]}\\ b_3^{[1]}\\ b_4^{[1]}\end{array}\right]$$
相加，显然我们会发现最终产生了一个4维列向量
而其中的每一个元素正是一次Logistic回归对应的结果
从而在输入层至隐藏层的正向传播中，上述向量化方法是合理的
对于隐藏层至输出层，我们亦进行同理的向量化
而对于：
$$x=\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]$$
我们仔细观察上图的神经网络结构
可以发现：
$$x=a^{[0]}$$
由此，向量化的神经网络正向传播过程可以表示为：
$$z^{[i]}=w^{[i]T}{a}^{[i-1]}+b^{[i]}$$
$$a^{[i]}=\sigma (z^{[i]})$$