入侵性杂草优化算法的改进与应用（Matlab代码实现）

           目录

1 概述

2 运行结果

3 参考文献

‍4 Matlab代码

---

1 概述

入侵杂草算法（IWO算法）是模拟杂草繁衍过程的一种随机搜索方法,具有鲁棒性、自适应性强和编程简单等优点,但也有搜索效率低,容易陷入局部最优的不足.在种群初始化阶段,研究者采用多子群法、反向学习法和混沌序列等方法使种群在全局空间分布更均匀;在空间扩散阶段,研究者将防早熟的杂草算法、Alopex算法、Lévy飞行法和蝙蝠算法等应用于IWO算法,使得部分种子在空间扩散阶段获得更强的全局搜索能力;在竞争排斥阶段,采用差分进化算法,可改善种群的多样性,并且更容易选择出优秀个体,提高收敛速度. 

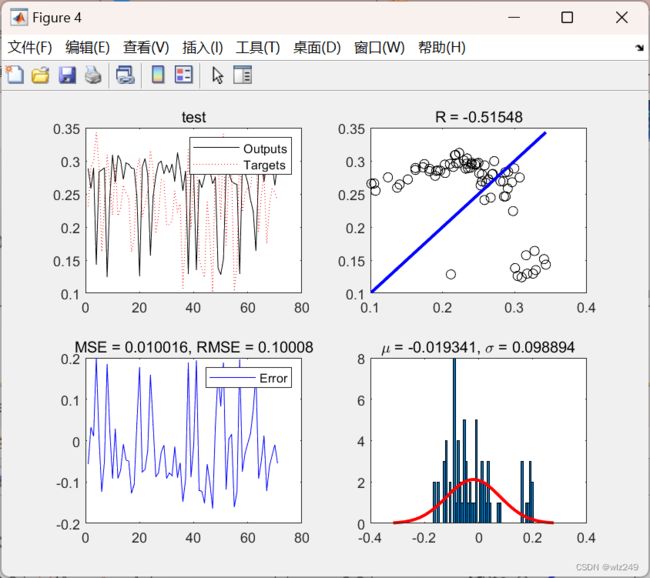
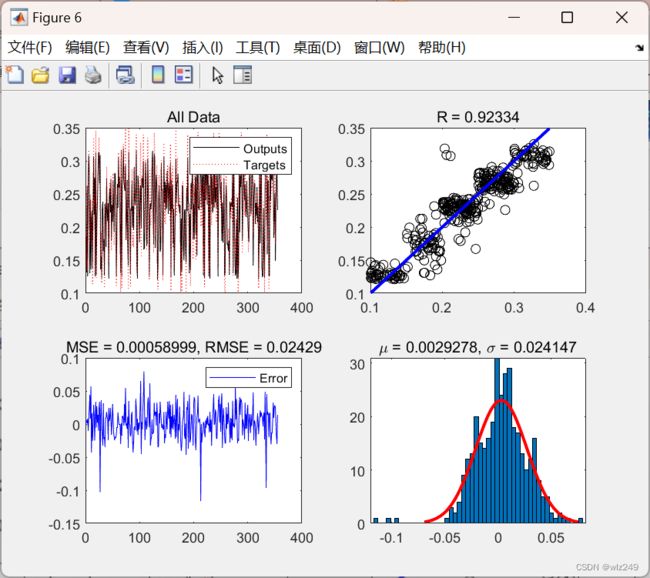
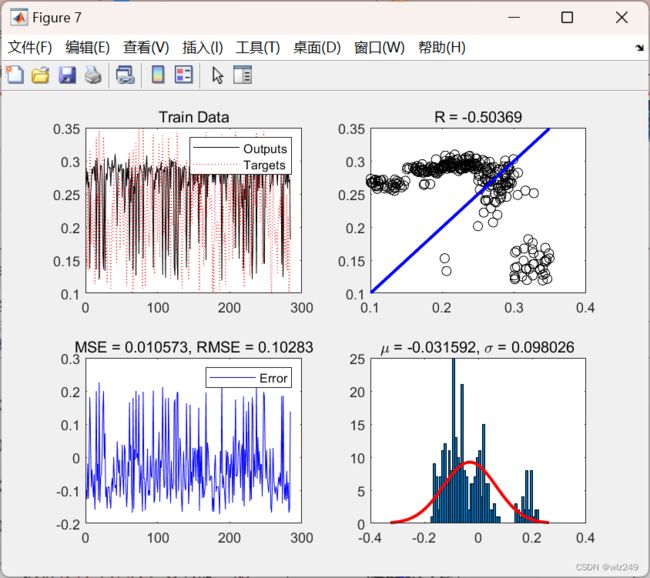
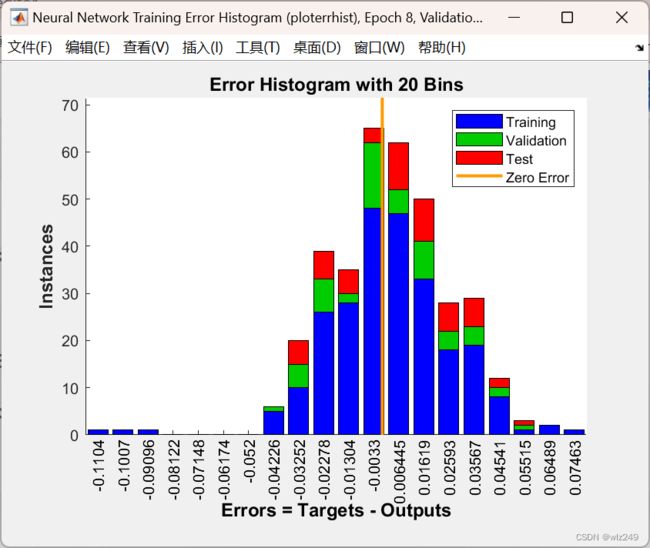
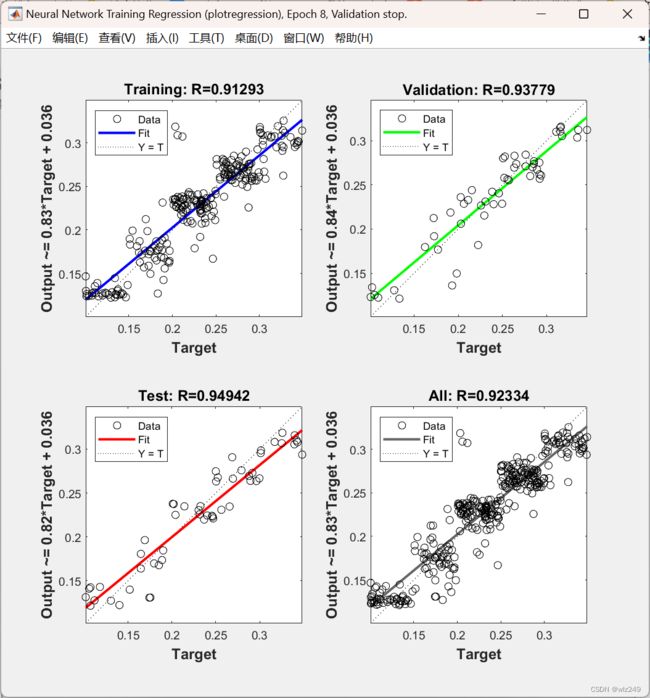
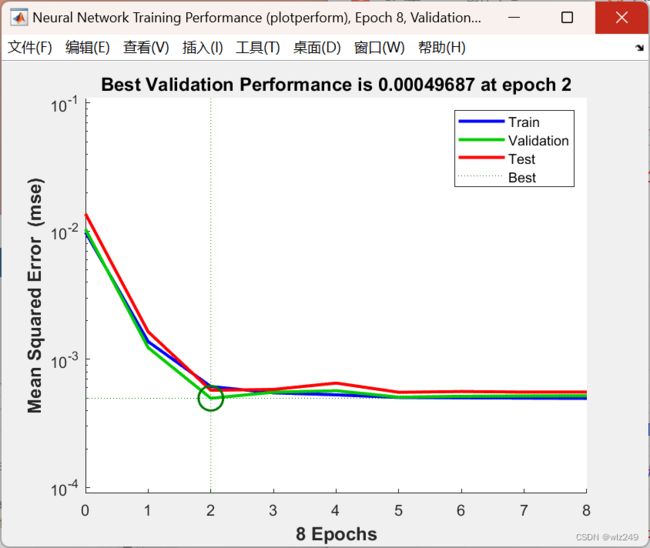
2 运行结果

 

 

 

 

 

 

 

 

3 参考文献

[1]周立军.入侵杂草算法及其改进方法综述[J].白城师范学院学报,2021,35(05):35-42.

‍4 Matlab代码

主函数部分代码：

clc;
clear;
close all;
format shortG
%% Insert Data

data=InsertData();

nvar = data.nvar;           % Number of Decision Variables
SizeX = [1 nvar];     % Decision Variables Matrix Size

lb = -1*ones(1,nvar);       % Lower Bound of Decision Variables
ub = 1*ones(1,nvar);        % Upper Bound of Decision Variables

%% IWO Parameters

Maxiter =200;    % Maximum Number of iterations

npop0 = 40;     % Initerial Population Size
npop = npop0*4;     % Maximum Population Size

Smin = 0;       % Minimum Number of Seeds
Smax = 5;       % Maximum Number of Seeds

Exponent = 2;           % Variance Reduction Exponent
sigma_initerial = 1;      % Initerial Value of Standard Deviation
sigma_final = 0.001;    % Final Value of Standard Deviation

%% Initerialization
tic
% Empty Plant Structure
emp.x = [];
emp.fit = [];
emp.info = [];

pop = repmat(emp, npop0, 1);    % Initerial Population Array

for i = 1:numel(pop)
    
    % Initerialize x
    pop(i).x = unifrnd(lb, ub);
    
    % Evaluation
    pop(i)= fitness(pop(i),data);
    
end

% Initerialize Best fit History
BEST = zeros(Maxiter, 1);

%% IWO Main Loop

for iter = 1:Maxiter
    
    % Update Standard Deviation
    sigma = ((Maxiter - iter)/(Maxiter - 1))^Exponent * (sigma_initerial - sigma_final) + sigma_final;
    
    % Get Best and Worst fit Values
    fits = [pop.fit];
    Bestfit = min(fits);
    Worstfit = max(fits);
    
    % Initerialize Offsprings Population
    newpop = [];
    
    % Reproduction
    for i = 1:numel(pop)
        
        ratio = (pop(i).fit - Worstfit)/(Bestfit - Worstfit);
        S = floor(Smin + (Smax - Smin)*ratio);
        
        for j = 1:S
            
            % Initerialize Offspring
            newsol = emp;
            
            % Generate Random Location
            newsol.x = pop(i).x + sigma * randn(SizeX);
            
            % Apply Lower/Upper Bounds
            newsol.x = CB(newsol.x, lb,ub);
       
            
            % Evaluate Offsring
            newsol = fitness(newsol,data);
            
            % Add Offpsring to the Population
            newpop = [newpop
                      newsol];  %#ok
            
        end
        
    end
    
    % Merge Populations
    [pop] = [pop
           newpop];
    
    % Sort Population
    [~, ind]=sort([pop.fit]);
    pop = pop(ind);

    % Competiterive Exclusion (Delete Extra Members)
    if numel(pop)>npop
        pop = pop(1:npop);
    end
    
    % Store Best Solution Ever Found
    gpop = pop(1); % gpop: global Solution
    
    % Store Best fit History
    BEST(iter) = gpop.fit;
    
    % Display iteration Information
    disp(['iter ' num2str(iter) ' Best = ' num2str(BEST(iter))]);
    
end