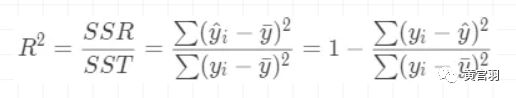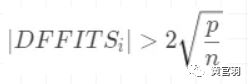线性回归建模思路与模型诊断(附代码)

• 分享笔者做线性回归的整体思路：确定因变量是否服从高斯分布；利用显著性检验寻找影响因变量的自变量；对自变量做必要的数据处理；模型建立与迭代

• 评估线性回归模型效果一般用可决系数R2

• 回归模型需要进行显著性检验(参数是否为0)和回归诊断(残差独立同分布)

• 多重共线性检测(自变量相关性)和强影响点分析（离群点）也是必要的
  

• 线性回归建模思路

在实战中，我们会面临很多特征，如何在众多特征中挑选哪些特征建立回归模型呢。特征选择与特征提取在不同场景中有不同的做法，笔者这里以自己的经验对线性回归建模做一个大体流程的分享。

step1：确定被研究的对象，也就是因变量y

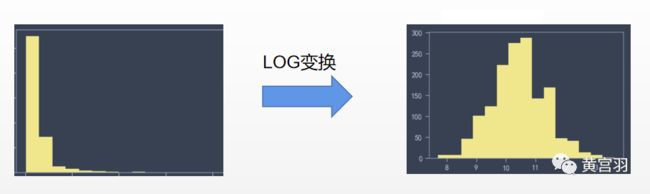
由于线性回归模型的假设是高斯分布。因此，对训练样本因变量做直方图与描述性统计，可以有个很好的判断。大多数情况，因变量Y可能不服从高斯分布，我们需要做一个线性变换，比如log。

注：上面数据随机捏造。python语法(plt.hist(y,bins=15,stacked=True,color='#F0E68C'))

为了进一步验证，我们需要用正态图进行检测目标y是否通过显著性检验，下面代码可以实现这个操作：

from scipy.stats import norm, skew


(mu, sigma) = norm.fit(y)
print(mu, sigma)
print('Kurtosis: %f' % y.kurt())
print('Skewness: %f' % y.skew())


fig = plt.figure(figsize=(4,3))
res = stats.probplot(y, plot=plt)
plt.show()

step2：对影响目标变量Y因素的整体探索

线性回归模型建立的自变量最好是能显著影响目标变量的，因此，挖掘哪些自变量会影响Y以及影响程度是一个必不可少的特征工程。笔者在这里分享自己的思路。

如果变量不多，就可以先从整体上观看每个自变量与Y的散点图，大概有个判断。除此外，结合实际业务场景也是一个必不可少的环节。下面代码实现了这个过程：

feature_list = []  #传入所有自变量
for i in feature_list:
    sns.pairplot(data,x_vars=i,y_vars=Y, plot_kws={'alpha': 0.5})
    plt.show()

step3:自变量与目标变量关系的显著性检验

散点图是一个比较粗略挖掘变量之间关系的图表，为了精确挖掘哪些变量对目标Y有影响。我们需要引进显著性检验的思想。这里分为离散型变量和连续型变量。

离散型变量主要是分为双样本假设检验和多样本假设检验（后者通常说的是方差分析）。其主要目的是验证每个变量的取值种类在目标Y上的均值是否有显著性差异。这里列出不同情况的检验方法。

注：关于假设检验以后也会专门出一期介绍。

双样本假设检验（特征取值只有两种，比如性别，只有男生女生）。

先进行方差齐性检验，利用下面代码可以实现这个过程：

a = data[data['性别'] == 0][Y]
b = data[data['性别'] == 1][Y]
leveneTestRes = stats.levene(a, b, center='median')
print('w-value=%6.4f, p-value=%6.4f' %leveneTestRes)

若p小于0.05，拒绝原假设，即两组数据方差不相同，有显著差异。

如果方差不相同，对于均值是否有显著差异不能使用t检验，要使用“大样本u检验”方法进行均值的假设检验。

利用大样本u检验的代码如下：

from scipy.stats import norm


des = data[Y].groupby(data['性别']).describe()
des['S'] = des['std']**2      #总体方差的无偏估计,describe内置的std分母是n-1


u = (des['mean'][0]-des['mean'][1])/np.sqrt(np.sum(des['S']/des['count'])) #构造检验统计量
p = norm.cdf(u,0,1) #概率密度函数在 负无穷 到 u上的积分，也就是概率


print('u-value=%6.4f, p-value=%6.4f' % (u,2*p))  #双侧检验，乘以2

如果方差齐性检验通过的前提下，可以采用t检验，下面利用三种方式进行验证，结果是一致的：

des = data[Y].groupby(data['性别']).describe()
des['S'] = des['std']**2      #总体方差的无偏估计,describe内置的std分母是n-1
a = data[data[f] == 0][Y]
b =data[data[f] == 1][Y]




#scipy内嵌模块估计
tTest = stats.ttest_ind(a,b)   #传入数组
print('t-value=%6.4f, p-value=%6.9f' % tTest)


#传入两组数据的均值、标准差和自由度
tTest = stats.ttest_ind_from_stats(des['mean'][0],des['std'][0],des['count'][0],des['mean'][1],des['std'][1],des['count'][1])
print('t-value=%6.4f, p-value=%6.9f' % tTest)




#手动实现
from scipy.stats import t
Sw = np.sqrt(np.sum(des['S']*(des['count']-1))/(np.sum(des['count'])-2))
t_v = (des['mean'][0]-des['mean'][1])/(Sw*np.sqrt(1/des['count'][0]+1/des['count'][1]))




if t_v >= 0 :
    p = 1-t.cdf(t_v,np.sum(des['count'])-2)
else:
    p = t.cdf(t_v,np.sum(des['count'])-2)


print('t-value=%6.4f, p-value=%6.9f' % (t_v,2*p))  #双侧检验，乘以2

多样本假设检验（方差分析）

如果离散变量取值多于两个，就要进行方差分析，找出显著影响因变量的特征。下面函数可以实现方差检验：

def box_figrue(f,degree=0):
'''
    :param f:离散变量名
    '''
    arg = []
    li = []
for i in df[f].unique():
        li.append(i)
        arg.append(df[df[f] == i][Y])
    sns.set_style('whitegrid')                                    #箱线图，观察异常值


    jtplot.style(ticks=True, grid=False, figsize=(6, 4.5))
    plt.rcParams['font.sans-serif']=['SimHei']
    plt.rcParams['axes.unicode_minus']=False


    sns.boxplot(data=arg,palette='deep')     #箱线图,设置6种颜色；调色板
    scale_ls = df[f].unique()
    index_ls = D[f]
    plt.xticks(scale_ls,index_ls,rotation=degree,fontsize=13)
    plt.xlabel(f,fontsize=15)
    plt.ylabel('Y')
    plt.show()


    f_test = stats.f_oneway(*arg)   #返回F统计值极其检验水平P


return f_test

经过检验统计后找出影响因变量的离散变量，但自变量之间若相关性很高，则只选取其中一个入模即可，也要进行对离散变量相关性的检验，我们知道，连续变量可以用相关系数刻画其相关性。而离散变量主要用到关联独立性检验。

它的目的是考察两个分类变量之间是否相关（独立）。如果它们之间不相关，那么由两个分类变量组成的列联表，列联表内每个单元格中的频数分布是随机而没有规律的，反之，则是服从一定比率的存在。

分为2*2列联表和R*C列联表，2*2列联表情况分为3中，而R*C直接使用皮尔逊卡方检验即可。下面代码可以实现这个检验过程：

from scipy import stats


#2*2列联表
def two_two_table(arr):
'''
    :param arr: 实际频数表,数组类型
    :return: 依次返回Fisher精确检验、连续性修正检验、皮尔逊卡方检验的p-value，以及适用的检验方式及检验结果
    '''


    fisher_p = stats.fisher_exact(arr,alternative='two-sided')          #Fisher精确检验（双侧检验）
    correct_chi_p = stats.chi2_contingency(arr)                         #连续性修正卡方检验
    chi_p = stats.chi2_contingency(arr,correction=False)                #皮尔逊卡方检验


    E = correct_chi_p[3].round(decimals=0)   #期望频数表
    n = E.sum()             #样本总频数


    a = np.any(E < 1)  #是否有小于1的期望频数单元格
    b = np.any((E < 5)&(E >=1)) #是否有大于等于1且小于5的期望频数单元格
    c = np.all(E >= 5)    #是否期望频数全部大于等于5


if n < 40 or a == True: #n小于40，或E小于1时，选择费舍尔精确检验结果
        test_result = fisher_p
        static = '费舍尔精确检验'
elif n >= 40 and b == True: #n大于等于40，且E大于1且小于5，选择连续性修正值
        test_result = correct_chi_p
        static = '连续性修正检验'
else: #n大于等于40，且E大于等于5，选择皮尔逊卡方值
        test_result = chi_p
        static = '皮尔逊卡方检验'


if test_result[1] < 0.05:
        re = '显著'
else:
        re = '不显著'


return arr,E,fisher_p[1],correct_chi_p[1],chi_p[1],static,test_result[0],test_result[1],re

分析连续变量与因变量的关系，通常要根据业务场景进行挖掘。但一般情况下，首先通过相关关系入手，然后从画出分析图进一步分析。必要情况需要做一些转换，使得其转换后的数据与因变量更加线性。

step4:数据处理

经过前面四步的挖掘，可以挑选出对因变量有影响的变量，当然，方法不止前面提到的。我们就能从基于筛选好的特征做归一化处理、降维等处理。这里没有提到数据的预处理，比如缺失值处理，异常点检测，因为这些是所有建模都要做的步骤，以后会出专题讲解，这里就当作数据已经提前做过预处理了。

step5:建模调参，循环迭代

最后一步就是建模调参的问题了，这一步需要反复实验，并把结果与业务场景联系起来，达到最优效果。

• 模型诊断
  

模型建成之后，我们需要评估模型的效果以及诊断回归模型的显著性，我们用可决系数评估模型的拟合效果，对模型进行显著性检验（参数显著性）和回归诊断（检验残差独立同分布），另外，还要考虑多重共线性和强影响点分析

1.拟合优度（可决系数R2）

回归直线与各观测点的接近程度成为回归直线对数据的拟合优度。而评判直线拟合优度需要一些指标，其中一个就是判定系数。

因变量y值有来自两个方面的影响：

（1）来自x值的影响，也就是我们预测的主要依据

（2）来自无法预测的干扰项ϵ的影响

如果一个回归直线预测非常准确，那么它就需要让来自x的影响尽可能的大，而让来自无法预测干扰项的影响尽可能的小，也就是说x影响占比越高，预测效果就越好。为此，定义以下指标：

• SST（总平方和）：总偏差平方和

• SSR（回归平方和）：由x与y之间的线性关系引起的y变化

• SSE（残差平方和）：除x影响之外的其它因素引起的y变化

• SST=SSR+SSE

SR越高，则代表回归预测越准确，观测点越是靠近直线，也即SSR/SST越大，直线拟合越好。因此，判定系数的定义就自然的引出来了，我们一般称为R2,也称可决系数。

举个例子说明可决系数的意义。

如小明想挖掘制作木偶的个数与成本的关系，建立回归方差后，求得模型的决定系数等于0.828。这表示大约83%的成本变化可以由模型解释，即83%的成本是由玩偶制作过程产生的。这部分成本是可控的，与生产个数是严格的线性关系。而剩下的17%是暂时未知的随机成本。

拓展：

上面定义的可决系数是最常用的，除此之外，还有其他定义的可决系数

2.线性回归显著性检验

根据样本拟合的模型是否可以有效地预测或估计，我们需要对拟合的模型进行显著性检验。回归分析中的显著性检验主要包括两方面内容：线性关系检验；回归系数检验。

线性关系检验是指多个自变量x和因变量y之间的线性关系是否显著，它们之间是否可以用一个线性模型表示。检验统计量使用F分布，其定义如下：

SSR的自由度为：自变量的个数k

SSE的自由度为：n-k-1

在多元线性回归中，只要有一个自变量系数不为零（即至少一个自变量系数与因变量有线性关系），我们就说这个线性关系是显著的。如果不显著，说明所有自变量系数均为零。

回归系数的显著性检验与线性检验不同，它要求对每一个自变量系数进行检验，然后通过检验结果可判断出自变量是否显著。因此，我们可以通过这种检验来判断一个特征（自变量）的重要性，并对特征进行筛选。检验统计量使用t分布

3.线性回归诊断

线性回归模型是基于一些假设条件的：除了自变量和因变量有线性相关关系外，其它假设基本都是关于残差的，主要就是残差ϵ独立同分布。

总结一下关于残差有三点假设：（1）正态性检验；（2）独立性检验；（3）方差齐性检验。

• 正态性检验

干扰项（即残差），服从正态分布的本质是要求因变量服从变量分布。

（1）直方图法

import statsmodels.formula.api as smf
import statsmodels.api as sm
# 创建线性回归最小二乘法模型
model = sm.OLS(yArr,xArr)
results = model.fit()
results.summary()


residual = results.resid
sns.distplot(residual,
bins = 10,
kde = False,
color = 'blue',
fit = stats.norm)
plt.show()

（2）PP图和QQ图

PP图是对比正态分布的累积概率值和实际分布的累积概率值。

QQ图是通过把测试样本数据的分位数与已知分布相比较，从而来检验数据的分布情况： 就是由标准正态分布的分位数为横坐标，样本值为纵坐标的散点图。

如果观察点都比较均匀的分布在直线附近，就可以说明变量近似的服从正态分布，否则不服从正态分布。

pq = sm.ProbPlot(residual)
pq.ppplot(line='45')
pq.qqplot(line='q')

（3）Shapiro检验

这种检验方法均属于非参数方法，先假设变量是服从正态分布的，然后对假设进行检验。一般地数据量低于5000则可以使用Shapiro检验，大于5000的数据量可以使用K-S检验

# shapiro检验
import scipy.stats as stats
stats.shapiro(residual)
out:
(0.9539670944213867, 4.640808128e-06)

上面结果两个参数：第一个是Shaprio检验统计量值，第二个是相对应的p值。可以看到，p值非常小，远远小于0.05，因此拒绝原假设，说明残差不服从正态分布。

• 独立性检验

残差的独立性可以通过Durbin-Watson统计量（DW）来检验。

原假设：p=0（即前后扰动项不存在相关性）

备择假设：p!=0（即近邻的前后扰动项存在相关性）

判断标准是：

p=0，DW=2：扰动项完全不相关

p=1，DW=0：扰动项完全正相关

p=-1，DW=4：扰动项完全负相关

• 方差齐性检验

如果残差随着自变量增发生随机变化，上下界基本对称，无明显自相关，方差为齐性，我们就说这是正常的残差。判断方差齐性检验的方法一般有两个：图形法，BP检验。

这里介绍BP法。

这种方法也是一种假设检验的方法，其原假设为：残差的方差为一个常数，然后通过计算LM统计量，判断假设是否成立。

# BP检验
sm.stats.diagnostic.het_breuschpagan(residual,results.model.exog)
out:
(0.16586685109032384,
0.6838114989412791,
0.1643444790856123,
0.6856254489662914)

上述参数：

第一个为：LM统计量值

第二个为：响应的p值，0.68远大于显著性水平0.05，因此接受原假设，即残差方差是一个常数

第三个为：F统计量值，用来检验残差平方项与自变量之间是否独立，如果独立则表明残差方差齐性

第四个为：F统计量对应的p值，也是远大于0.05的，因此进一步验证了残差方差的齐性。

4.多重共线性检验

当回归模型中两个或两个以上的自变量彼此相关时，则称回归模型中存在多重共线性，也就是说共线性的自变量提供了重复的信息。

影响：会造成回归系数，截距系数的估计非常不稳定，即整个模型是不稳定。这种不稳定的具体表现是：很可能回归系数原来正，但因为共线性而变为负。这对于一些自变量的可解释性来讲可能是致命的，因为得到错误系数无法解释正常发生的现象。

多重共线性有很多检测方法，最简单直接的就是计算各自变量之间的相关系数，并进行显著性检验。具体的，如果出现以下情况，可能存在多重共线性：

（1）模型中各对自变量之间显著性相关。

（2）当模型线性关系（F检验）显著时，几乎所有回归系数的t检验不显著。

（3）回归系数的正负号与预期的相反。

（4）方差膨胀因子（VIF）检测，一般认为VIF大于10，则存在严重的多重共线性。

from statsmodels.stats.outliers_influence import variance_inflation_factor
# from statsmodels.tools.tools import add_constant
def checkVIF_new(df):   #方差膨胀因子
    df.insert(0,'constant',1)  #添加常数项
    name = df.columns
    x = np.matrix(df)
    VIF_list = [variance_inflation_factor(x,i) for i in range(x.shape[1])]
    VIF = pd.DataFrame({'feature':name,"VIF":VIF_list})
    return VIF

多重共线性对于线性回归是种灾难，并且我们不可能完全消除，而只能利用一些方法来减轻它的影响。对于多重共线性的处理方式，有以下几种思路：

（1）提前筛选变量：可以利用相关检验来或变量聚类的方法。

（2）子集选择：包括逐步回归和最优子集法。

（3）收缩方法：正则化方法，包括岭回归和LASSO回归.

（4）维数缩减：包括主成分回归（PCR）和偏最小二乘回归（PLS）方法。

5.强影响点分析

强影响点指的就是离散点。这个很容易联想到，如果有一些离散点远离大部分数据，那么拟合出来的模型可能就会偏离正常轨迹，受到影响。因此，在做线性回归诊断分析的时候也必须把这些强影响点考虑进去，进行分析。

（1）学生化残差

学生化残差（SR）指残差标准化后的数值。一般的当样本量为几百时，学生化残差大于2的点被视为强影响点，而当样本量为上千时，学生化残差中大于3的点为相对大的影响点。

（2）Cook's D统计量

Cook‘s D统计量用于测量当第i个观测值从分析中去除时，参数估计的改变程度。一般的Cook's D值越大说明越可能是离散点，没有很明确的临界值。建议的影响临界点是：Cook's D > 4/n，即高于此值可被视为强影响点。

（3）DFFITS统计量

用于测量第i个观测值对预测值的影响。建议的临界值为

（4）DFBETAS统计量

用于测量当去除第i个观测量时，第j个参数估计的变化程度。建议的影响临界值为

# 强离散点各个指标
from statsmodels.stats.outliers_influence import OLSInfluence
import statsmodels.api as sm
model = sm.OLS(yArr,xArr).fit()
OLSInfluence(model).summary_frame().head()
# 单独获取各个指标
ol = model.get_influence()
leverage = ol.hat_diag_factor
dffits = ol.dffits
resid_stu = ol.resid_studentized_external
cook = ol.cooks_distance

参考资料：

《概率论与数理统计教程第二版》

https://mp.weixin.qq.com/s/XfuuoF8r9qxUdIXKWpoPow