【模型代码】astgcn
astgcn的结构
这是好久以前写的,还是第一次学那么深的代码。因为啥都不会,所以什么都想分析一波。导致笔记的框架没有搭好。需要仔细审才能看明白。不适合小白!
文章目录
- astgcn的结构
-
- 一、`class Spatial_Attention_layer(nn.Block)`
-
- 1.1简介内容
- 1.2原理
-
- Spatial attention
- 二、`class cheb_conv_with_SAT(nn.Block)`
-
- 2.1 简介内容
- 2.2 原理
- 2.3 参数进入讲解
- 三、`class Temporal_Attention_layer(nn.Block)`
- 四、`class ASTGCN_block(nn.Block)`:
- 五、`class ASTGCN_submodule(nn.Block)`
-
- 5.1 参数介绍
- 5.2 模型搭建
-
- 5.2.1 两个`ST block`
- 5.2.2 全连接层
- 5.3 forward函数
- 六、`class ASTGCN(nn.Block)`
一、class Spatial_Attention_layer(nn.Block)
1.1简介内容
有两个函数_init和forward
- 定义初始化并创建权重w、偏差by以及(不知道的)V 共5个参数
- 定义forward函数,参数初始化、进行前向计算、标准化
class Spatial_Attention_layer(nn.Block):
'''
# 空间注意力层
compute spatial attention scores 计算空间注意力得分
'''
def __init__(self, **kwargs):
super(Spatial_Attention_layer, self).__init__(**kwargs) # 采用 nn.Block 的初始化
with self.name_scope():
# 通过get函数从“共享”字典中检索,找不到则创建Parameter,声明需要名字和尺寸
# 创建这些参数,并允许延迟初始化
self.W_1 = self.params.get('W_1', allow_deferred_init=True) # allow_deferred_init 允许延迟初始化
self.W_2 = self.params.get('W_2', allow_deferred_init=True)
self.W_3 = self.params.get('W_3', allow_deferred_init=True)
self.b_s = self.params.get('b_s', allow_deferred_init=True)
self.V_s = self.params.get('V_s', allow_deferred_init=True)
def forward(self, x):
'''
Parameters
----------
x: mx.ndarray, x^{(r - 1)}_h,
shape is (batch_size, N, C_{r-1}, T_{r-1}) # 样本个数,顶点个数,特征个数,时间长度
Returns
----------
S_normalized: mx.ndarray, S', spatial attention scores
shape is (batch_size, N, N)
'''
# get shape of input matrix x 获得输入矩阵的维数
_, num_of_vertices, num_of_features, num_of_timesteps = x.shape
# defer the shape of params 延迟参数的形状
self.W_1.shape = (num_of_timesteps, ) # W_1 \in R^{T_{r-1}}
self.W_2.shape = (num_of_features, num_of_timesteps) #,W_2\ in R^{C_{r-1}\times T_{r-1}}
self.W_3.shape = (num_of_features, ) # W_3 \in R^{C_{r-1}}
self.b_s.shape = (1, num_of_vertices, num_of_vertices) # b_s \in R^{1\times N \times N}
self.V_s.shape = (num_of_vertices, num_of_vertices) # V_s \in R^{ N \times N}
for param in [self.W_1, self.W_2, self.W_3, self.b_s, self.V_s]:
param._finish_deferred_init() # 去完成原来要求延迟初始化的数据。
1.2原理
Spatial attention
目的:使用注意机制【2017】自适应的捕捉空间中的节点之间的动态相关性。
案例:以 recent component 中的spatial attention 为例介绍
S = V s ⋅ σ ( ( X h ( r − 1 ) W 1 ) W 2 ( W 3 X h ( r − 1 ) ) T + b s ) (1) S=V_s \cdot \sigma ( (\mathcal{X}^{(r-1)}_{h}W_1) \ W_2\ (W_3\mathcal{X}^{(r-1)}_h)^T \ +b_s) \tag{1} S=Vs⋅σ((Xh(r−1)W1) W2 (W3Xh(r−1))T +bs)(1)
- ( X h ( r − 1 ) W 1 ) W 2 (\mathcal{X}^{(r-1)}_{h}W_1)W_2 (Xh(r−1)W1)W2: 左乘
lhs = nd.dot(nd.dot(x, self.W_1.data()), self.W_2.data())
- 多维数组矩阵乘法,前面保持相同不变,只动后两位
- x:(batch_size,顶点个数,特征个数,时间长度) W_1:(时间长度) w_2:(特征个数,时间长度)
- x乘以W_1:(batch_size,顶点个数,特征个数)
- x乘以W_1再乘以W_2:(batch_size,顶点个数,时间长度)
- ( W 3 X h ( r − 1 ) ) T (W_3\mathcal{X}^{(r-1)}_h)^T (W3Xh(r−1))T:右乘
rhs = nd.dot(self.W_3.data(), x.transpose((2, 0, 3, 1)))
- 多维数组矩阵乘法,前面保持相同不变,只动后两位
- w_3:(特征个数) X.tran:(特征个数,batch_size,时间长度,顶点个数)
- 这里的x转置只是为了让w_3和x能够相乘
- w_3乘以x转置:(batch_size,时间长度,顶点个数)
- 左乘 × \times ×右乘
product = nd.batch_dot(lhs, rhs)
左乘和右乘后的结果(batch_size,顶点个数,顶点个数)
- ReLU激活后再乘以 V s V_s Vs
S = nd.dot(self.V_s.data(), # shape:(顶点个数,顶点个数) ,估计类似于一个缩放吧
nd.sigmoid(product + self.b_s.data())
# 乘积+偏置->送入激活函数中,激活后的结果进行一个转置变为(顶点个数,顶点个数,batch_size)
.transpose((1, 2, 0)))\
# v_s 和 转职后的结果 的点乘积的shape为 (顶点个数,顶点个数,batch_size)
.transpose((2, 0, 1)) # 最终的结果再转置为(batch_size,顶点个数,顶点个数)
S i , j ′ = e x p ( S i , j ) ∑ j = 1 N e x p ( S i , j ) (2) S'_{i,j}=\frac{exp(S_{i,j})}{\sum^N_{j=1}exp(S_{i,j})} \tag{2} Si,j′=∑j=1Nexp(Si,j)exp(Si,j)(2)
- 使用softmax函数标准化
# normalization # 使用softmax函数标准化
S = S - nd.max(S, axis=1, keepdims=True)
exp = nd.exp(S)
S_normalized = exp / nd.sum(exp, axis=1, keepdims=True)
return S_normalized
其中:
X h ( r − 1 ) = ( X 1 , X 2 , . . . , X T r − 1 ) ∈ R N × C r − 1 × T r − 1 \mathcal{X}^{(r-1)}_h=(X_1,X_2,...,X_{T_{r-1}}) \in R^{N\times C_{r-1} \times T_{r-1}} Xh(r−1)=(X1,X2,...,XTr−1)∈RN×Cr−1×Tr−1 是spatial-temporal block 的第r次输入
C r − 1 C_{r-1} Cr−1是第r层的数据输入的通道大小。
σ \sigma σ是激活函数
S(注意力矩阵)是根据该层的当前输入动态计算的。
S i , j ∈ S S_{i,j}\in S Si,j∈S 表示节点i&节点j 之间的相关强度。然后使用softmax函数确保节点的attention weights的和为1.
特别的:
当 r = 1 , C 0 = F r=1,C_0=F r=1,C0=F时, T r − 1 T_{r-1} Tr−1 时第r层的时间维度的长度
当 r = 1 , T 0 = T h r=1,T_0=T_h r=1,T0=Th时(或 T 0 = T d T_0=T_d T0=Td,或 T 0 = T w T_0=T_w T0=Tw), V s , b s ∈ R N × > N , W 1 ∈ R T r − 1 , W 2 ∈ R C r − 1 × T r − 1 , W 3 ∈ R C r − 1 V_s,b_s \in R^{N\times >N},W_1 \in R^{T_{r-1}},W_2\in R^{C_{r-1}\times T_{r-1}},W_3 \in R^{C_{r-1}} Vs,bs∈RN×>N,W1∈RTr−1,W2∈RCr−1×Tr−1,W3∈RCr−1都是可学习的参数。
用途:当执行GCN时,我们将邻接矩阵A和空间注意力矩阵S结合起来动态调整节点之间的权重。
二、class cheb_conv_with_SAT(nn.Block)
2.1 简介内容
功能:具有空间注意分数的K阶chebyshev图卷积
有两个函数_init_&forward
- 定义初始化,定义变量 切比雪夫多项式的项数k,输入特征,过滤器数量 并创建参数 Θ \Theta Θ
- 定义forward函数,
class cheb_conv_with_SAt(nn.Block):
'''
K-order chebyshev graph convolution with Spatial Attention scores
具有空间注意分数的K阶chebyshev图卷积
'''
def __init__(self, num_of_filters, K, cheb_polynomials, **kwargs):
'''
Parameters
----------
num_of_filters: int
num_of_features: int, num of input features
K: int, up K - 1 order chebyshev polynomials
will be used in this convolution
'''
super(cheb_conv_with_SAt, self).__init__(**kwargs)
self.K = K
self.num_of_filters = num_of_filters # 图卷积层用的过滤器的个数(类似于神经元的个数)
self.cheb_polynomials = cheb_polynomials # 应该是切比雪夫多项式的每一项(基)的列表
with self.name_scope():
self.Theta = self.params.get('Theta', allow_deferred_init=True) # 创建参数\Theta并延迟初始化
def forward(self, x, spatial_attention):
'''
Chebyshev graph convolution operation 切比雪夫图卷积操作
Parameters
----------
x: mx.ndarray, graph signal matrix
shape is (batch_size, N, F, T_{r-1}), F is the num of features
spatial_attention: mx.ndarray, shape is (batch_size, N, N)
spatial attention scores 空间注意力的得分有batch_size个
Returns
----------
mx.ndarray, shape is (batch_size, N, self.num_of_filters, T_{r-1})
'''
(batch_size, num_of_vertices,
num_of_features, num_of_timesteps) = x.shape
self.Theta.shape = (self.K, num_of_features, self.num_of_filters) # 设置参数\Theta的形状,具体参考文献
self.Theta._finish_deferred_init() # 参数具备形状,完成初始化
2.2 原理
在《一》中我们采用空间注意机制方法得到了注意力矩阵S。通过注意力矩阵S和临近矩阵调整后,输入到空间卷积中,然后进行空间上的卷积,空间上的卷积是GCN,采用的是切比雪夫多项式的方式。 k − 1 k-1 k−1阶多项式,抓取的是以每个节点为中心的周围0~k-1阶邻居的信息。最后再用ReLU作为最终激活函数。
1. 图G上的信号x经过 核 g θ g_{\theta} gθ 的过滤为:
g θ ∗ G x = g θ ( L ) x = g θ ( U Λ U T ) x = U g θ ( Λ ) U T x (5) g_{\theta} \ast G \ x =g_{\theta}(L)x=g_{\theta}(U\Lambda U^T)x=Ug_{\theta}(\Lambda)U^Tx \tag{5} gθ∗G x=gθ(L)x=gθ(UΛUT)x=Ugθ(Λ)UTx(5)
理解:由于图信号的卷积运算等于这些信号通过图傅里叶变换变换到谱域的乘积。可以理解为将 g θ 和 x g_{\theta}和x gθ和x分别不安换到谱域,然后将他们的变换结果相乘,并进行傅里叶逆变换,得到卷积运算的结果。
然而,当图的规模较大时,直接对拉普拉斯矩阵进行特征值分解是费力的。因此,采用切比雪夫多项式有效的近似解决这个问题。
2. 切比雪夫多项式近似:
g θ ∗ G x = g θ ( L ) x = ∑ k = 0 K − 1 θ k T k ( L ~ ) x (6) g_{\theta}\ast G\ x =g_{\theta}(L)x =\sum^{K-1}_{k=0}\theta_k T_k(\tilde{L})x \tag{6} gθ∗G x=gθ(L)x=k=0∑K−1θkTk(L~)x(6)
注意到:
θ ∈ R K \theta \in R^K θ∈RK 是多项式的系数向量
L ~ = 2 λ m a x L − I N \tilde{L}=\frac{2}{\lambda_{max}}L-I_N L~=λmax2L−IN将L变换到(0~1)之间为 L ~ \tilde{L} L~, λ m a x \lambda_{max} λmax是拉普拉斯矩阵的最大特征值
3. 切比雪夫多项式的递归项:
| 切比雪夫多项式 | 对矩阵的切比雪多项式 |
|---|---|
| T 0 ( x ) = 1 T_0(x)=1 T0(x)=1 | T 0 ( L ) = I T_0(L)=I T0(L)=I |
| T 1 ( x ) = x T_1(x)=x T1(x)=x | T 1 ( L ) = L T_1(L)=L T1(L)=L |
| T k ( x ) = 2 x T k − 1 ( x ) − T k − 2 ( x ) T_k(x)=2xT_{k-1}(x)-T_{k-2}(x) Tk(x)=2xTk−1(x)−Tk−2(x) | T k ( L ) = 2 L T k − 1 ( L ) − T k − 2 ( L ) T_k(L)=2LT_{k-1}(L)-T_{k-2}(L) Tk(L)=2LTk−1(L)−Tk−2(L) |
4. 动态调整节点之间的相关性
g θ ∗ G x = g θ ( L ) x = ∑ k = 0 K − 1 θ k ( T k ( L ~ ⊙ S ′ ) x ) g_{\theta} \ast G \ x=g_{\theta}(L)x=\sum^{K-1}_{k=0}\theta_k(T_k(\tilde{L}\odot S')x) gθ∗G x=gθ(L)x=k=0∑K−1θk(Tk(L~⊙S′)x)
其中
S ′ ∈ R N × N S' \in R^{N \times N} S′∈RN×N
X ~ h ( r − 1 ) = ( X 1 ~ , X 2 ~ , . . . , X ~ T r − 1 ) ∈ R N × C r − 1 × T r − 1 \tilde{\mathcal{X}}^{(r-1)}_h=(\tilde{X_1},\tilde{X_2},...,\tilde{X}_{T_{r-1}}) \in R^{N\times C_{r-1} \times T_{r-1}} X~h(r−1)=(X1~,X2~,...,X~Tr−1)∈RN×Cr−1×Tr−1,得知 X ~ t ∈ R N × C r , t = 1 , 2 , . . , T r − 1 \tilde{X}_t \in R^{N\times C_r},t =1,2,..,T_{r-1} X~t∈RN×Cr,t=1,2,..,Tr−1注意到这里 X ~ h ( r − 1 ) \tilde{\mathcal{X}}^{(r-1)}_h X~h(r−1)而不是 X h r − 1 X_h^{r-1} Xhr−1,这里的 X ~ h ( r − 1 ) \tilde{\mathcal{X}}^{(r-1)}_h X~h(r−1)是对 X h r − 1 X_h^{r-1} Xhr−1经过时间注意力调整后的结果,具体看<三>
我们看到最后一维是时间长度,而具体到每个时间片t,对应有 X t ~ \tilde{X_t} Xt~,执行 C r C_r Cr(第r层时空块)个filter(类似于神经元),得到 g θ ∗ G X t ~ g_{\theta} \ast G \ \tilde{X_t} gθ∗G Xt~
Θ = ( Θ 1 , Θ 2 , . . , Θ C r ) R K × C r − 1 × C r \Theta=(\Theta_1,\Theta_2,..,\Theta_{C_r})\R^{K\times C_{r-1}\times C_r} Θ=(Θ1,Θ2,..,ΘCr)RK×Cr−1×Cr,得知 Θ i ∈ R K × C r − 1 , i = 1 , 2 , . . , C r \Theta_i \in R^{K\times C_{r-1}},i=1,2,..,C_r Θi∈RK×Cr−1,i=1,2,..,Cr,也就是说 Θ i \Theta_i Θi是过滤器filter $ C_i$的切比雪夫多项式的系数向量。
因此, Θ i 中 的 维 度 k \Theta_i中的维度k Θi中的维度k表示k-1阶多项式的系数个数,而 C r − 1 C_{r-1} Cr−1表示的是特征个数。
outputs = []
for time_step in range(num_of_timesteps): # 对于每个时间片t,t=1,2,..T_{r-1}
# shape is (batch_size, V, F)
graph_signal = x[:, :, :, time_step] # 具体到每个时间片time_step的数据
output = nd.zeros(shape=(batch_size, num_of_vertices,
self.num_of_filters), ctx=x.context) # 用于存放一层卷积后的结果(一层有num_of_filter个‘神经元’)
for k in range(self.K): # 多项式的每一项
# shape of T_k is (V, V)
T_k = self.cheb_polynomials[k] # 多项式基中的第k项,shape为(顶点个数,顶点个数)
# shape of T_k_with_at is (batch_size, V, V)
T_k_with_at = T_k * spatial_attention # 基经过空间注意力矫正后
# shape of theta_k is (F, num_of_filters)
theta_k = self.Theta.data()[k] # 矫正后的多项式基[k]的对应项的系数\theta[k],shape为(特征个数,‘神经元’个数)
# shape is (batch_size, V, F)
# T_k_with_at.transpose((0,2,1))==>batch_size的个数不变,对矫正后的基进行一个转置
rhs = nd.batch_dot(T_k_with_at.transpose((0, 2, 1)),
graph_signal) # 矫正基乘以图信号 因为相乘的两个元素中都有batch_size,可以理解为批量矩阵乘法
output = output + nd.dot(rhs, theta_k) # 矫正基乘以图信号的结果再乘以对应项的系数,最后求和
outputs.append(output.expand_dims(-1)) # expand_dims 扩展维数(-1)是在最后一维得未知增添一维。
# output.expand_dims(-1) 是由(batch_size,顶点,过滤器个数)变为(batch_size, 顶点,过滤器个数,1)
# outputs是output得列表,根据最后一维拼接得话,经过nd.concat(*outputs,dim=-1)得到得是(batch_size,顶点,过滤器个数,时间)
return nd.relu(nd.concat(*outputs, dim=-1)) # 最后使用relu函数激活
2.3 参数进入讲解
‘K’:K
num_of_chev_filter:64
这两个参数,应用到che_conv_with_SAT这一层网络中,输入为 X ~ 得 s h a p e : ( b a t c h s i z e , N , F , T ) \tilde{X}得shape:(batchsize,N,F, T) X~得shape:(batchsize,N,F,T)
GCN层关键是参数 Θ \Theta Θ,且一个参数对应一个卷积(‘神经元’)同时对应一个通道,这里用到得参数为num_of_chev_filter:64
对于每一个时间步骤num_of_timesteps来说 :
- 每一个拉普拉斯算子对图信号 X ~ \tilde{X} X~得作用过程为:
rhs = nd.batch_dot(T_k_with_at.transpose((0, 2, 1)),
graph_signal) # 矫正基乘以图信号 因为相乘的两个元素中都有batch_size,可以理解为批量矩阵乘法
其中rhs得shape为(batch_size, 顶点,特征)
- 作用结果为:
注意到,这是在每一个K里面完成得
output = output + nd.dot(rhs, theta_k) # 矫正基乘以图信号的结果再乘以对应项的系数,最后求和
theta_k得shape为(K,特征个数,过滤器个数)
output得shape为(batch_size,顶点,过滤器个数)=【(batch_size,顶点,特征)乘以(特征,过滤器个数)】这k步得结果相加
- output最后一维升维
outputs.append(output.expand_dims(-1)) # expand_dims 扩展维数(-1)是在最后一维得未知增添一维。
# output.expand_dims(-1) 是由(batch_size,顶点,过滤器个数)变为(batch_size, 顶点,过滤器个数,1)
# outputs是output得列表,根据最后一维拼接得话,经过nd.concat(*outputs,dim=-1)得到得是(batch_size,顶点,过滤器个数,时间)
return nd.relu(nd.concat(*outputs, dim=-1)) # 最后使用relu函数激活
- 采用激活函数relu
返回得结果得shape是(batch_size,顶点,过滤器个数,时间)
总结 :
数据是(batch_size,顶点,特征,时间)
参数为K和过滤器个数
结果为(batch_size,顶点,过滤器个数,时
三、class Temporal_Attention_layer(nn.Block)
与<一>同理
E = V e ⋅ σ ( ( ( X h ( r − 1 ) ) T U 1 ) U 2 ( U 3 X h ( r − 1 ) ) + b e ) (3) E=V_e \cdot \sigma (( (\mathcal{X}^{(r-1)}_{h})^T U_1) \ U_2\ (U_3\mathcal{X}^{(r-1)}_h) \ +b_e) \tag{3} E=Ve⋅σ(((Xh(r−1))TU1) U2 (U3Xh(r−1)) +be)(3)
E i , j ′ = e x p ( E i , j ) ∑ j = 1 T r − 1 e x p ( E i , j ) (4) E'_{i,j}=\frac{exp(E_{i,j})}{\sum^{T_{r-1}}_{j=1}exp(E_{i,j})} \tag{4} Ei,j′=∑j=1Tr−1exp(Ei,j)exp(Ei,j)(4)
其中
V e , b e ∈ R T r − 1 × T r − 1 V_e,b_e \in R^{T_{r-1}\times T_{r-1}} Ve,be∈RTr−1×Tr−1 U 1 ∈ R N U_1 \in R^N U1∈RN, U 2 ∈ R C r − 1 × N U_2 \in R^{C_{r-1}\times N} U2∈RCr−1×N U 3 ∈ R C r − 1 U_3 \in R^{C_{r-1}} U3∈RCr−1
E i , j ∈ E E_{i,j} \in E Ei,j∈E在语义上表示节点i&j之间的的依赖关系强度。最后,E被softmax函数规范化。
输入: X h ( r − 1 ) = ( X 1 , X 2 , . . . , X T r − 1 ) ∈ R N × C r − 1 × T r − 1 \mathcal{X}^{(r-1)}_h=(X_1,X_2,...,X_{T_{r-1}}) \in R^{N\times C_{r-1} \times T_{r-1}} Xh(r−1)=(X1,X2,...,XTr−1)∈RN×Cr−1×Tr−1
输出: X ~ h ( r − 1 ) = ( X 1 ~ , X 2 ~ , . . . , X ~ T r − 1 ) = ( X 1 , X 2 , . . . , X T r − 1 ) E ′ ∈ R N × C r − 1 × T r − 1 \tilde{\mathcal{X}}^{(r-1)}_h=(\tilde{X_1},\tilde{X_2},...,\tilde{X}_{T_{r-1}}) =(X_1,X_2,...,X_{T_{r-1}})E' \in R^{N\times C_{r-1} \times T_{r-1}} X~h(r−1)=(X1~,X2~,...,X~Tr−1)=(X1,X2,...,XTr−1)E′∈RN×Cr−1×Tr−1
四、class ASTGCN_block(nn.Block):
整体来说,是对图5得一个时空搭建。用到了前面得《一、二、三》
这一个章节解读一个class,因为方便解读代码,所以,划分为好几个部分。
- 传入的参数并在这个类中赋值
class ASTGCN_block(nn.Block):
# 对fig5的一个整体时空块的搭建
def __init__(self, backbone, **kwargs):
'''
Parameters
----------
backbone: dict, should have 6 keys, 有6个关键字的字典
"K", 切比雪夫多项式的阶数为K-1
"num_of_chev_filters", 空间图卷积层的'神经元’个数
"num_of_time_filters", 时间卷积层的‘神经元’个数
"time_conv_kernel_size", 时间卷积层的过滤器的尺寸大小
"time_conv_strides", 时间卷积层的滑动步子
"cheb_polynomials" 切比雪夫多项式基的列表
'''
super(ASTGCN_block, self).__init__(**kwargs) # 按照nn.Block的方式初始化
K = backbone['K']
num_of_chev_filters = backbone['num_of_chev_filters']
num_of_time_filters = backbone['num_of_time_filters']
time_conv_strides = backbone['time_conv_strides']
cheb_polynomials = backbone["cheb_polynomials"]
- 构建模型每一层的网络对象
with self.name_scope(): # 同一个scope空间下
self.SAt = Spatial_Attention_layer() # 对 空间注意力层 的实例化
# 对 基于空间注意力矩阵的切比雪夫多项式图卷积层 的实例化
self.cheb_conv_SAt = cheb_conv_with_SAt(
num_of_filters=num_of_chev_filters, # 参数,切比雪夫图卷积层的‘神经元’个数
K=K, # 参数,切比雪夫多项式的基的个数
cheb_polynomials=cheb_polynomials) # 参数,切比雪夫多项式的基的列表
self.TAt = Temporal_Attention_layer() # 对 时间注意力层 的实例化
# 对 时间卷积层的2维CNN卷积层 的实例化
self.time_conv = nn.Conv2D(
channels=num_of_time_filters, # 参数,时间卷积层的‘神经元’个数
kernel_size=(1, 3), # 参数,时间卷积层过滤器的核的大小
padding=(0, 1), # 参数,时间卷积层的填充情况
strides=(1, time_conv_strides)) # 参数,时间卷积层的过滤器移动步骤
self.residual_conv = nn.Conv2D( # 对 残差卷积层->2维CNN卷积层 的实例化
channels=num_of_time_filters, # 参数, 时间卷积层的‘神经元’个数
kernel_size=(1, 1), # 参数, 核的大小
strides=(1, time_conv_strides)) # 参数, 过滤器的移动步骤
self.ln = nn.LayerNorm(axis=2) # 归一化层,对于一个样本案例(而不是batch_size个样例)的所有通道的结果做一个集合,根据这个集合进行归一化
画流程图示意:
- 根据以上流程图,做前向计算,定义
forward函数
def forward(self, x):
'''
Parameters
----------
x: mx.ndarray, shape is (batch_size, N, C_{r-1}, T_{r-1}) (batch_size, 顶点个数,特征个数,时间长度)
Returns
----------
mx.ndarray, shape is (batch_size, N, num_of_time_filters, T_{r-1})
'''
(batch_size, num_of_vertices,
num_of_features, num_of_timesteps) = x.shape
# 得到E', shape is (batch_size, T, T)
temporal_At = self.TAt(x) # TAt 是时间注意力层,根据数据x得到(时间长度,时间长度)的注意力矩阵E',含批量batch_size
# X^=X点乘E'
x_TAt = nd.batch_dot(x.reshape(batch_size, -1, num_of_timesteps), # x转换维度 (batch_size, 顶点个数*特征个数,时间长度)
temporal_At)\ # 时间注意力矩阵E'转换维度(batch_size, 时间长度, 时间长度)
.reshape(batch_size, num_of_vertices, # 批量乘法的结果为 (batch_size, 顶点个数*特征个数,时间长度)
num_of_features, num_of_timesteps) # 批量后的结果reshape为 (batch_size, 顶点个数,特征个数,时间长度)
# cheb gcn with spatial attention
# 通过X^得到S‘
spatial_At = self.SAt(x_TAt)
# 对x和S'进行cheb gcn 操作 结果为(batch_size, 顶点个数,’神经元‘个数,时间长度)
spatial_gcn = self.cheb_conv_SAt(x, spatial_At)
# convolution along time axis 进行时间轴上的卷积
time_conv_output = (self.time_conv(spatial_gcn.transpose((0, 2, 1, 3)))
.transpose((0, 2, 1, 3)))
解释 :
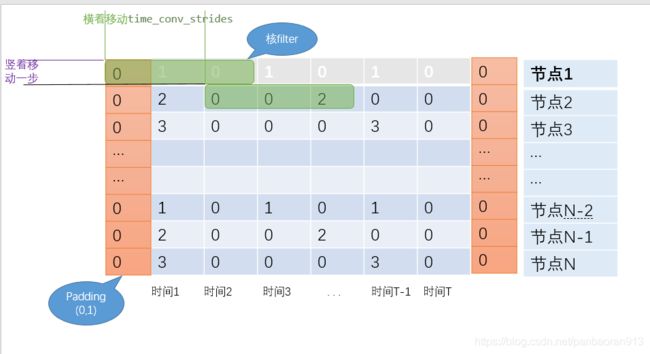
在时间上的2维CNN卷积
spatial_gcn.tran ->(batch_size, ’神经元‘个数,顶点个数,时间长度T
time_conv:
通道 核大小 padding strides '神经元’个数 (1,3) (0,1) (1,time_conv_strides)
# residual shortcut
x_residual = (self.residual_conv(x.transpose((0, 2, 1, 3)))
.transpose((0, 2, 1, 3)))
'''
x: (batch_size, 顶点个数,特征个数,时间长度) x.tran->(batch_size,特征个数,顶点个数,时间长度)
resi_conv: 通道->'神经元’个数, 核大小->(1,1) padding->无 strides->(1,time_conv_strides)
根据公式,顶点个数那列:N 时间长度: [(T-1)除以time_conv_strides]+1
'''
return self.ln(nd.relu(x_residual + time_conv_output))
# self.ln 是对样本做层归一化
五、class ASTGCN_submodule(nn.Block)
5.1 参数介绍
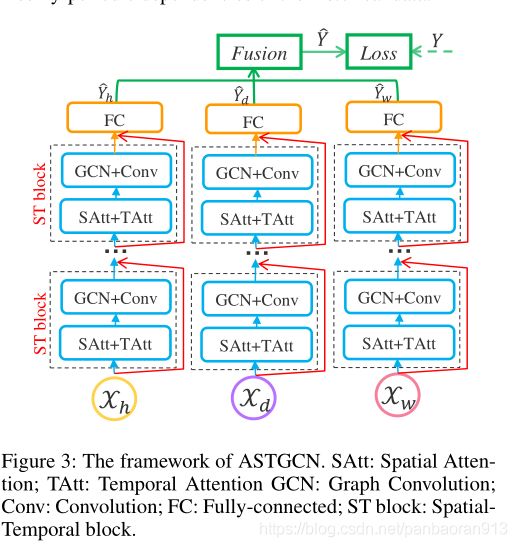
从图中可以看到,模型结构的框架。
all_backbones=[backbones1,backbones2,backbones3]
结合上图所示,模型总框架包含左中右三个框架。
backbones1=[{字典1},{字典2}] backbones2=[{字典3},{字典4}] backbones3=[{字典5},{字典6}]
结合图所示,在每个bachbones中有两个ST block,每一个ST block的模型框架参数由字典所确定。
ST block是在《三》中解释,可以看流程图示意。
每个字典的参数如下。
“K”, 切比雪夫多项式的阶数为K-1
“num_of_chev_filters”, 空间图卷积层的’神经元’个数
“num_of_time_filters”, 时间卷积层的‘神经元’个数
“time_conv_kernel_size”, 时间卷积层的过滤器的尺寸大小 # 在模型中自己定义的,不需要传参“time_conv_strides”, 时间卷积层的滑动步子
“cheb_polynomials” 切比雪夫多项式基的列表
class ASTGCN_submodule(nn.Block):
'''
a module in ASTGCN
'''
def __init__(self, num_for_prediction, backbones, **kwargs):
'''
Parameters
----------
num_for_prediction: int, how many time steps will be forecasting
backbones: list(dict), list of backbones
'''
super(ASTGCN_submodule, self).__init__(**kwargs) # 按照nn.Block的初始化方式定义
5.2 模型搭建
可以看到左中右任何一个模型都是具有两个ST block+FC,重要的是按照顺序的方式排列的。
5.2.1 两个ST block
self.blocks = nn.Sequential() # 创建一个 顺序的容器Sequential ,实例化
for backbone in backbones: # backbones 是一个列表,里面的元素backbone是一个(含6个key的)字典
self.blocks.add(ASTGCN_block(backbone)) # ASTGCN_block(backbone) 是一个实例化(backbone会传入到_init_函数中)
解释:
nn.Sequential(),是创建一个顺序容器,里面依次添加网络中的各种层结构(nn.Block的子类)
案例示意:以右侧侧第一个为案例:对应的week_sample的数据 X w e e k X_{week} Xweek
backbones1=[
{“K”: K,
“num_of_chev_filters”: 64,
“num_of_time_filters”: 64,
“time_conv_strides”: num_of_weeks, # 7*24 # 时间卷积层的滑动步子
“cheb_polynomials”: cheb_polynomials # 固定已知},
{“K”: K,
“num_of_chev_filters”: 64,
“num_of_time_filters”: 64,
“time_conv_strides”: 1 # 时间卷积层的滑动步子
“cheb_polynomials”: cheb_polynomials # 固定已知}]
以上是整个时空块的模型结构,我们将时空块的参数带进去,看效果如何。
对于第一个时空块
- 对于che_conv_with_SAT层
参数’K’:K
参数num_of_chev_filter:64
参数cheb_polynomials
数据是(batch_size,顶点,特征3,时间)
结果为(batch_size,顶点,过滤器个数64,时间)
- 对于time_conv_out层
参数channels=num_oftime_filters:64
strides(1,time_conv_strides):num_of_week
输入是(batch_size,顶点,过滤器个数64,时间)转置后为(batch_size, 过滤器个数64,顶点N,时间T)
时间卷积后得结果为(batch_size,过滤器个数64,顶点不变N,时间为 [ ( T − 1 ) / ( t i m e − c o n v − s t r i d e s ) + 1 ] [(T-1)/(time-conv-strides)+1] [(T−1)/(time−conv−strides)+1])
- 对于residual_conv层
参数channels=num_oftime_filters:64
strides(1,time_conv_strides):num_of_week
输入是(batch_size, 顶点,特征3,时间)转置后为(batch_size,特征个数64,顶点个数,时间)
残差卷积层后得结果为(batch_size,过滤器个数64,顶点不变N,时间为 [ ( T − 1 ) / ( t i m e − c o n v − s t r i d e s ) + 1 ] [(T-1)/(time-conv-strides)+1] [(T−1)/(time−conv−strides)+1])
卷积转置后得结果为(batch_size,顶点N,过滤器个数64,时间为 [ ( T − 1 ) / ( t i m e − c o n v − s t r i d e s ) + 1 ] [(T-1)/(time-conv-strides)+1] [(T−1)/(time−conv−strides)+1])
- 对于relu层和layer Normalization层
结果不变(batch_size,顶点N,过滤器个数64,时间为 [ ( T − 1 ) / ( t i m e − c o n v − s t r i d e s ) + 1 ] [(T-1)/(time-conv-strides)+1] [(T−1)/(time−conv−strides)+1])
对于第二个时空块
对于che_conv_with_SAT层
参数’K’:K
参数num_of_chev_filter:64
参数cheb_polynomials
数据是(batch_size,顶点N,过滤器个数64,时间为 [ ( T − 1 ) / ( t i m e − c o n v − s t r i d e s ) + 1 ] [(T-1)/(time-conv-strides)+1] [(T−1)/(time−conv−strides)+1])
结果为(batch_size,过滤器个数64,顶点不变N,时间为 [ ( T − 1 ) / ( t i m e − c o n v − s t r i d e s ) + 1 ] [(T-1)/(time-conv-strides)+1] [(T−1)/(time−conv−strides)+1])
- 对于time_conv_out层
参数channels=num_oftime_filters:64
strides(1,time_conv_strides):num_of_week
输入是(batch_size,过滤器个数64,顶点不变N,时间为 [ ( T − 1 ) / ( t i m e − c o n v − s t r i d e s ) + 1 ] [(T-1)/(time-conv-strides)+1] [(T−1)/(time−conv−strides)+1])
转置后为(batch_size,顶点不变N,过滤器个数64,时间为 [ ( T − 1 ) / ( t i m e − c o n v − s t r i d e s ) + 1 ] [(T-1)/(time-conv-strides)+1] [(T−1)/(time−conv−strides)+1])
时间卷积后得结果为(batch_size,过滤器个数64,顶点不变N,时间为 [ ( T − 1 ) / ( t i m e − c o n v − s t r i d e s ) + 1 ] [(T-1)/(time-conv-strides)+1] [(T−1)/(time−conv−strides)+1])
- 对于residual_conv层
参数channels=num_oftime_filters:64
strides(1,time_conv_strides):num_of_week
输入是结果不变(batch_size,顶点N,过滤器个数64,时间为 [ ( T − 1 ) / ( t i m e − c o n v − s t r i d e s ) + 1 ] [(T-1)/(time-conv-strides)+1] [(T−1)/(time−conv−strides)+1])
转置后为(batch_size,过滤器个数64,顶点不变N,时间为 [ ( T − 1 ) / ( t i m e − c o n v − s t r i d e s ) + 1 ] [(T-1)/(time-conv-strides)+1] [(T−1)/(time−conv−strides)+1])
残差卷积层后得结果为(batch_size,过滤器个数64,顶点不变N,时间为 [ ( T − 1 ) / ( t i m e − c o n v − s t r i d e s ) + 1 ] [(T-1)/(time-conv-strides)+1] [(T−1)/(time−conv−strides)+1])
卷积转置后得结果为(batch_size,顶点N,过滤器个数64,时间为 [ ( T − 1 ) / ( t i m e − c o n v − s t r i d e s ) + 1 ] [(T-1)/(time-conv-strides)+1] [(T−1)/(time−conv−strides)+1])
- 对于relu层和layer Normalization层
结果不变(batch_size,顶点N,过滤器个数64,时间为 [ ( T − 1 ) / ( t i m e − c o n v − s t r i d e s ) + 1 ] [(T-1)/(time-conv-strides)+1] [(T−1)/(time−conv−strides)+1])
5.2.2 全连接层
经过两个时空块后喂入全连接层,进行预测。
with self.name_scope():
# use convolution to generate the prediction 使用卷积生成预测
# instead of using the fully connected layer 而不是使用全连接层
self.final_conv = nn.Conv2D( # 2维CNN卷积
channels=num_for_prediction, # 预测的个数
kernel_size=(1, backbones[-1]['num_of_time_filters'])) # 核的大小
self.W = self.params.get("W", allow_deferred_init=True) # 获取权重参数 W ,并允许延迟初始化
final_conv层是一个2维CNN层
channels=num_for_prediction(预测个数,12,6,3)
kernel_size=(1,最后一个时空块中得过滤器数量)
5.3 forward函数
def forward(self, x):
'''
Parameters
----------
x: mx.ndarray,
shape is (batch_size, num_of_vertices,
num_of_features, num_of_timesteps)(batch_size, 顶点个数,特征个数,时间长度)
Returns
----------
mx.ndarray, shape is (batch_size, num_of_vertices, num_for_prediction)(batch_size,顶点个数,预测个数)
'''
x = self.blocks(x) # 将数据x 喂入层block
module_output = (self.final_conv(x.transpose((0, 3, 1, 2)))
[:, :, :, -1].transpose((0, 2, 1)))
'''
经过block后得x是 (batch_size,顶点N,过滤器64,时间[(T-1)除以time_conv_strides]+1)
经过转置后是 (batch_size,时间[(T-1)除以time_conv_strides]+1,顶点N,过滤器64)
2维卷积单通道结果 (batch_size,1, 顶点N,1 )
2维卷积结果维 (batch_size,预测数目, 顶点N,1 )
降维后得结果 (batch_size,预测数目, 顶点N)
转置后得结果 (batch_size,顶点N, 预测数目)
'''
_, num_of_vertices, num_for_prediction = module_output.shape
self.W.shape = (num_of_vertices, num_for_prediction)
self.W._finish_deferred_init()
return module_output * self.W.data()
# (batch_size,顶点个数,预测数目) 点乘 (顶点个数,预测数目)=(batch_size, 顶点个数, 预测数目)
六、class ASTGCN(nn.Block)
如图3所以得全部框架。
class ASTGCN(nn.Block):
'''
ASTGCN, 3 sub-modules, for hour, day, week respectively
'''
def __init__(self, num_for_prediction, all_backbones, **kwargs):
'''
Parameters
----------
num_for_prediction: int, how many time steps will be forecasting
all_backbones: list[list],
3 backbones for "hour", "day", "week" submodules
'''
super(ASTGCN, self).__init__(**kwargs)
# 保证骨干里面有元素
if len(all_backbones) <= 0:
raise ValueError("The length of all_backbones "
"must be greater than 0")
self.submodules = [] # 存放左中右三个模型得结果
with self.name_scope():
for backbones in all_backbones:
self.submodules.append(
ASTGCN_submodule(num_for_prediction, backbones))
self.register_child(self.submodules[-1])
def forward(self, x_list):
'''
Parameters
----------
x_list: list[mx.ndarray],
shape is (batch_size, num_of_vertices,
num_of_features, num_of_timesteps)
Returns
----------
Y_hat: mx.ndarray,
shape is (batch_size, num_of_vertices, num_for_prediction)
'''
# 保证数据类个数和三个模型得个数相等
if len(x_list) != len(self.submodules):
raise ValueError("num of submodule not equals to "
"length of the input list")
num_of_vertices_set = {i.shape[1] for i in x_list} # 数据列表中顶点集个数集合
if len(num_of_vertices_set) != 1: # 如果顶点得个数不唯一,则报错
raise ValueError("Different num_of_vertices detected! "
"Check if your input data have same size"
"at axis 1.")
batch_size_set = {i.shape[0] for i in x_list} # 数据列表中batch_size得集合
if len(batch_size_set) != 1: # 如果集合中元素不唯一,则报错
raise ValueError("Input values must have same batch size!")
submodule_outputs = [self.submodules[idx](x_list[idx]) # 搞不明白两个数据集之间到底在干嘛
for idx in range(len(x_list))]
return nd.add_n(*submodule_outputs) # 将三个模型得预测结果加起来