【论文阅读】Quantum Approximate Optimization Algorithm for Bayesian network structure learning
综述
如题,开创性将量子近似优化算法(QAOA)应用于学习贝叶斯网络结构。实验结果表明算法有效且对量子噪声具有定量的弹性,并在现实数据集上得到验证。
Introduction
贝叶斯网络(Bayesian networks)
一种概率图模型,表达一组随机变量的联合概率分布。
下面是wikipedia上的例子,RAIN是下雨,SPRINKLER是洒水车作业,GRASS WET是草地湿了,R和S会导致G,而R也会影响S,雨天时洒水车通常不工作,对应有概率分布表。
https://en.wikipedia.org/wiki/Bayesian_network

BNs研究的两个主要问题:①观察到一些变量,如何计算特定变量的后验概率,这个还是比较复杂的;②网络的结构学习,这也是论文的研究方向,一开始看到Bayesian以为是要研究概率问题,没想到是研究网络,图。

BNs是有向无环图(DAG),对于 n n n个节点的DAG的可能结构数如下式,随着 n n n增加,结构数指数增长,因此贝叶斯的结构学习是NP-hard问题。

Structure learning of Bayesian networks
通过 ( G , Θ ) (G,\Theta) (G,Θ)描述一个BN,G是图结构,每个随机变量对应图中一个节点,弧代表变量之间具有概率相关性, Θ \Theta Θ是父子节点之间条件概率,对应上面例子的概率分布表。
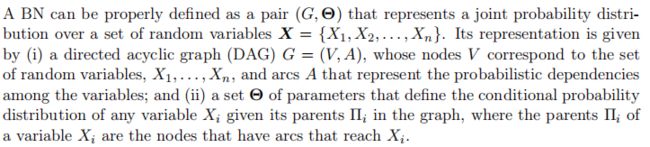
贝叶斯网络结构学习的三种主要方法:(1)基于分数,优化评估结构质量的函数;(2)基于约束,执行一些统计测试考察变量之间的条件独立性;(3)hybrid method,前面两种方法的结合。论文采用第一种方法,评价函数如下

其中 D D D是dataset, G G G是DAG, Π i \Pi_i Πi是图中的父节点,相当于将原图分解为以 Π i \Pi_i Πi为根的子图(树)进行考察。
QUBO formulation of BNSL
QUBO: quadratic unconstrained optimization problem,即无约束二次规划问题(QP问题)
BNSL:Bayesian network structure learning
QUBO公式如下
![]()
H s c o r e H_{score} Hscore优化基于输入数据结构的可能性,贝叶斯的优化目标,让已经发生的尽可能发生;
H m a x H_{max} Hmax限制节点入度以限制哈密顿量的复杂性;
H t r a n s H_{trans} Htrans和 H c o n s i s t H_{consist} Hconsist保证邻接矩阵对应的BN是DAG.
其中 A , R , Y A,R,Y A,R,Y依次是量子比特关联的邻接矩阵,拓扑序以及最大入度。
需要的量子比特数
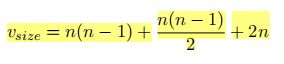
邻接矩阵需要 n ( n − 1 ) n(n-1) n(n−1)个量子比特,排除矩阵对角线元素对应的 n n n个自环,拓扑序需要 n ( n − 1 ) / 2 n(n-1)/2 n(n−1)/2个,最大入度需要 2 n 2n 2n个。
1. H s c o r e ( A ) H_{score}(A) Hscore(A)
邻接矩阵 A A A:
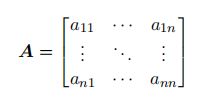
拆解,通过 a i j a_{ij} aij定义:

其中 a i a_i ai表示矩阵的第 i i i列, H s c o r e i ( a i ) H_{score}^i(a_i) Hscorei(ai)为每一列的得分, ∏ j ∈ J a j i \prod_{j\in J}a_{ji} ∏j∈Jaji这一项保证 j j j是存在的边, w i ( J ) w_i(J) wi(J)定义:
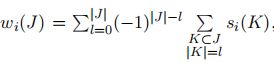
其中 s i ( K ) s_i(K) si(K)为节点 i i i父亲集合的得分,这个表达有点类似容斥定理。
节点 i i i没有父亲节点,则 w i ( ∅ ) = s i ( ∅ ) w_i(\emptyset)=s_i(\emptyset) wi(∅)=si(∅);若有一个父亲节点 j j j,可以按定义展开,发现就是父亲的得分 s i ( { X j } ) s_i(\{X_j\}) si({Xj}):
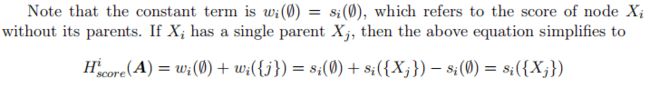
有两个父亲 j j j和 k k k:
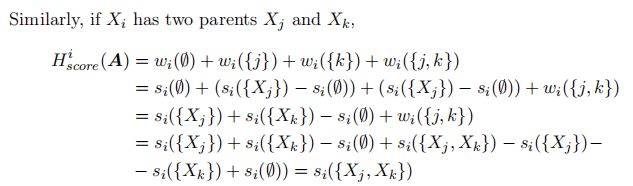
感觉这个“巧妙”的定义,最后对于节点 i i i而言,其父亲集合为 P i = { . . . } P_i=\{...\} Pi={...},最后 H s c o r e i ( a i ) = s i ( P i ) H_{score}^i(a_i)=s_i(P_i) Hscorei(ai)=si(Pi),可能还是要去读引用论文才能更好地理解。
2. H m a x ( A , Y ) H_{max}(A,Y) Hmax(A,Y)
![]()

最大入度限制为2, y i j y_{ij} yij是松弛变量,将节点入度的不等式约束转为等式约束,具体作用为,当 d i ≤ m d_i\leq m di≤m时 y i y_i yi取 m − ∑ j = 1 n a i j m-\sum^n_{j=1}a_{ij} m−∑j=1naij使得 H = 0 H=0 H=0;否则取0。 δ m a x \delta_{max} δmax为惩罚系数项。
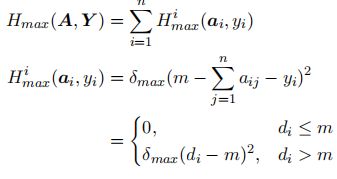
3. H t r a n s ( R ) H_{trans}(R) Htrans(R)和 H c o n s i s t ( A , R ) H_{consist}(A,R) Hconsist(A,R)

通过一个矩阵 R t o p R_{top} Rtop表征拓扑序,以满足无环的约束。

因为 r i j = 1 r_{ij}=1 rij=1时, r j i r_{ji} rji一定为0,实际上我们只需 n ( n − 1 ) 2 \frac{n(n-1)}{2} 2n(n−1)个元素就可以表达所有偏序关系,因此使用去除对角线及一下元素的矩阵 R R R即可,最终哈密顿量公式表达:

| r i j r_{ij} rij | r i k r_{ik} rik | r j k r_{jk} rjk | H t r a n s i j k H_{trans}^{ijk} Htransijk |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1( δ m a x \delta_{max} δmax) |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1( δ m a x \delta_{max} δmax) |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
实际上就是表达了两种成环的情况,注意 r i j = 0 r_{ij}=0 rij=0的话 r j i = 1 r_{ji}=1 rji=1, i ≤ j ≤ k ≤ i i\leq j\leq k \leq i i≤j≤k≤i中的不等号表达的是偏序关系,并不是大小。至于为什么只考察三个点形成的环,因为图一定包含 n ( n − 1 ) 2 \frac{n(n-1)}{2} 2n(n−1)条弧,两点之间一定存在弧,只是方向不确定。对于更大的环一定对应存在三个点的环,反之,不存在三个点的环,也就不存在环,这时 R R R矩阵是可传递的。

H c o n s i s t ( A , R ) H_{consist}(A,R) Hconsist(A,R)用于保证邻接矩阵 A A A和偏序矩阵 R R R的一致性,至于为什么通过三个矩阵去表达一个DAG,个人猜想是将不等约束转换为等式约束,方便后面用量子比特进行表达。
两种不一致的情况: a j i = a i j = 1 a_{ji}=a_{ij}=1 aji=aij=1和 a i j = 1 ∧ r i j = 0 a_{ij}=1\wedge r_{ij}=0 aij=1∧rij=0.
Quantum Approximate Optimization Algorithm

一个组合优化问题可以通过 n n n个比特和 m m m个子句描述,每个子句由比特集合的子集描述,满足时赋予特定的值。优化目标是最大化以下表达:

其中 z z z是位串,由 n n n个比特位拼接而来, C α ( z ) = 0 C_{\alpha}(z)=0 Cα(z)=0当且仅当子句 α \alpha α不满足。
QAOA算法通过一个量子参数电路(variational ansatz)表达特定的组合优化问题以及量子参数状态。在每轮迭代中,搜索可以找到位串 z ′ z' z′使得 C ( z ′ ) C(z') C(z′)最大化的参数。量子电路包含 p p p层,每层包含两个算子,编码目标函数的 U ( H c , γ ) U(H_c,\gamma) U(Hc,γ):
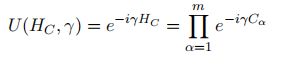
以及混合单调算子 U ( H B , β ) U(H_B,\beta) U(HB,β):