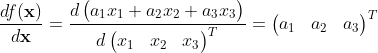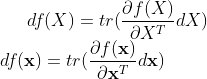矩阵求导(本质、原理与推导)详解
矩阵求导是机器学习与深度学习的基础,它是高等数学、线性代数知识的综合,并推动了概率论与数理统计向多元统计的发展。在一般的线性代数的课程中,很少会提到矩阵导数的概念;而且在网上寻找矩阵求导的知识点,也是五花八门,各有各的说法,各有各自的定义,好多东西也是很容易弄得混淆。那么兔兔今天就从头到尾详细讲解矩阵求导的本质,原理与一般解法的推导。
一:认识函数,认识自变量(变元)
认识函数,认识自变量是非常重要的,这是我们的立足点。回顾高数中的知识,我们大部分情况下遇到的都是自变量是一个数,值是一个数,函数的作用是把一个数映射成另一个数。但是也有自变量是多个数,值是一个数(即多元函数)。
那么在从传统的高等数学向矩阵延伸时,自变量就不一定是一个数了。自变量可以是一个数,可以是多个数(多个数是一个向量或是一个矩阵);经函数映射处理后得到的值以是一个数,一个向量或矩阵。至于值是数还是向量、矩阵,与函数function有关。
这样我们就把自变量分成数,向量,矩阵三种,我们也可以把自变量叫做函数function的变元。把函数function分成三种:function是标量、向量、矩阵,我们就把function分别叫做——实值标量函数(映射成数)、实向量函数(映射成向量)、实矩阵函数(映射成矩阵)。
(1)function是实标量函数(用f表示),其变元是标量(用x表示)
这个其实就是我们最最常见的一元函数。比如![]() ,
,![]() 等。它就是把一个数映射成另一个数。
等。它就是把一个数映射成另一个数。
(2)function是实标量函数(用f表示),其变元是向量(用x或![]() 表示)
表示)
如果我们纸上书写,最好用![]() 表示,便于区分,而在电脑上一般用加粗表示向量。
表示,便于区分,而在电脑上一般用加粗表示向量。
对于这种情况,就是高数中的多元函数。只不过自变量的多元我们用向量表示,并且我们通常都认为是列向量(这个是约定俗成的东西,而且大家用同样的标准,交流起来也很方便)。例如![]() ,变元x就是
,变元x就是![]() ;
; ![]() ,变元x就是
,变元x就是![]() 。
。
(3)function是实标量函数(用f表示),其变元是矩阵(用X表示)
(4)function是实向量函数(用f或![]() 表示),其变元是标量(用x表示)。
表示),其变元是标量(用x表示)。
这时function就是把一个数x映射成向量。例如![]() ,里面的f1,f2,f3其实就是前面讲的实标量函数。组合成向量形成的就是一个实向量函数。
,里面的f1,f2,f3其实就是前面讲的实标量函数。组合成向量形成的就是一个实向量函数。
(5)function是实向量函数(用f或![]() 表示),其变元是向量(用x或
表示),其变元是向量(用x或![]() 表示)。
表示)。
这时function把向量映射成向量。例如,x=
![]() 。和刚才一样,里面f1,f2,f3是实标量函数,每个都把向量映射成数,又把数排列一起成向量。
。和刚才一样,里面f1,f2,f3是实标量函数,每个都把向量映射成数,又把数排列一起成向量。
注意:我们在高数等其它教材或是网上看到的“向量函数(vector function)”对应的就是该(5)条的情形。那里的向量函数定义是:从![]() 的映射。对应这里就是function是m维的,把n维向量x在function作用下映射成m维向量。
的映射。对应这里就是function是m维的,把n维向量x在function作用下映射成m维向量。
(6)function是实向量函数(用f或![]() 表示),其变元是矩阵(用X表示)
表示),其变元是矩阵(用X表示)
例子就是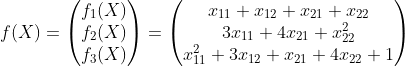 。变元就是
。变元就是![]() 。它其实就是把矩阵映射成了向量。里面f1,f2,f3分别把矩阵X映射成数,也就是(3)那一部分。
。它其实就是把矩阵映射成了向量。里面f1,f2,f3分别把矩阵X映射成数,也就是(3)那一部分。
(7)function是实矩阵函数(用F表示),其变元是标量(用x表示)。
(8)function是实矩阵函数(用F表示),其变元是向量(用x或![]() 表示)。
表示)。
把向量映射成矩阵。向量维数是变元维数,矩阵维数是实矩阵函数维数。,其中变元
![]() 。
。
(9)function是实矩阵函数(用F表示),其变元是矩阵(用X表示)。
到这里应该就很好理解了,,
总结:我们可以发现,最终的值是数、向量还是矩阵与函数有关——函数是几维的向量或矩阵,相应值就是几维的数或矩阵。并且我们在写的过程中都是把向量f或矩阵F拆解成最小单元f,用一元函数f分别计算数x、向量x或矩阵X,得到的数按原来对应的f位置堆叠。无论变元是向量还是矩阵,我们最终都是把它拆成单个数x,集体代入f中计算。
| 标量变元 | 向量变元 | 矩阵变元 | |
|---|---|---|---|
| 实值标量函数 | |||
| 实向量函数 | |||
| 实矩阵函数 |
一会儿兔兔会告诉你们,我们之后很少遇到给定的这样的复杂的函数。更多的是AX、bxa等这样的函数,把它们展开其实就是对应上面的样子啦。
二:理解这些函数的导数。
导数,无外乎就是函数对自变量求导。由于函数与自变量在这里已经延申到向量、矩阵,肯定与以往既有区别,又有联系。
对于(1)的情况,兔兔不必再讲了,它就是普通的一元函数求导。
对于(2)和(3)的情况,其实就是求偏导了。比如![]() ,分别对x1,x2,x3求偏导(也就是对变元
,分别对x1,x2,x3求偏导(也就是对变元![]() 求导),再排列成向量,结果就是
求导),再排列成向量,结果就是![]() ,其实写成列向量和行向量关系倒不是很大(一会儿讲布局时细说)。
,其实写成列向量和行向量关系倒不是很大(一会儿讲布局时细说)。
如果是f(X)对X求导,那就分别对里面xij求导,结果分别写在矩阵i行j列处(这个就是梯度矩阵)梯度矩阵: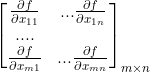 。把梯度矩阵转置,就是Jacobian矩阵。第三种就是把矩阵按列堆栈向量化,比如
。把梯度矩阵转置,就是Jacobian矩阵。第三种就是把矩阵按列堆栈向量化,比如 ,vec(X) (堆栈化)后就是
,vec(X) (堆栈化)后就是![]() 。之后操作就是向量求导了。如果是这样的列向量,求导后的列向量就叫做梯度向量,把它转置就叫做行向量偏导。除了堆栈向量化,这四个矩阵稍微了解就好,不同特意去记它们。
。之后操作就是向量求导了。如果是这样的列向量,求导后的列向量就叫做梯度向量,把它转置就叫做行向量偏导。除了堆栈向量化,这四个矩阵稍微了解就好,不同特意去记它们。
当实向量函数f(x)对数x求导,就是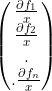 ,其中
,其中![]() 。实矩阵函数对单个数的求导,把实矩阵函数堆栈化,像刚才一样分别抽走第1列,2列...首尾连接成一个向量,然后求导。
。实矩阵函数对单个数的求导,把实矩阵函数堆栈化,像刚才一样分别抽走第1列,2列...首尾连接成一个向量,然后求导。
那么对于(1)(2)(3)(4)(7)的情况,不是函数是单个的,就是变元是单个数,求导也很容易理解。其中(3)需要对变元堆栈化,(7)对函数堆栈化。
那么问题就来了,其它的该怎样求导呢?求导又该怎样排布呢?
这里又一个很大的坑——分子布局、分母布局与混合布局。
由于在布局方面没有统一的标准,导致我们在看其它文章时各有各的结果,很容易把我们搞糊涂。所以我们十分有必要了解这三种布局的情况。
我们先看(5),实向量函数对向量变元求导。‘
比如f(x),向量函数为2维,即![]() ,变元
,变元![]() 为3维的向量。那么
为3维的向量。那么![]() 对x求导,就是f1分别对x1,x2,x3求偏导,再f2对x1,x2,x3求偏导。分子布局,就是分子是列向量形式,分母是行向量形式。对这个例子来说,就是求导后的矩阵第1行全是f1分别对x1,x2,x3求导,第2行是f2对x求导,那么矩阵就是2x3维(行数是函数维数,列数是变元维数)。
对x求导,就是f1分别对x1,x2,x3求偏导,再f2对x1,x2,x3求偏导。分子布局,就是分子是列向量形式,分母是行向量形式。对这个例子来说,就是求导后的矩阵第1行全是f1分别对x1,x2,x3求导,第2行是f2对x求导,那么矩阵就是2x3维(行数是函数维数,列数是变元维数)。。分母布局,就是分母是列向量,分子是行向量。求导后是刚才分子分布的转置。
。那么,对于刚才(2)的情况,咱们当时说无论排成行还是列向量,关系不是很大,准确来说就是——如果是分子布局,结果就是列向量;分母布局,结果就是行向量(因为分母布局定义:分母是行向量形式,分子是列向量,此时只不过分母是一个数)。
简单来说,分子就代表函数,分母就是变元,是什么分布,什么就是列向量,另一个就是行向量。而且如果是分子布局,实向量函数是列向量形式,导数结果当中f1,f2,f3也相应是竖着的,第一行是f1对x求导,第二行是f2对x求导......。分母布局对应也是如此。至于选哪种布局计算,其实都可以的。一旦求导时分子和分母的形式确定了,布局也就确定了,结果也就是唯一的。
其实,只要知道实向量函数对向量求导的方法。其余的就容易很多了。只要碰到矩阵,堆栈化成向量就可以了,之后再考虑用哪个布局。比如实矩阵函数对矩阵求导,分别把函数、矩阵变元堆栈化就可以了。
三:由定义尝试求一些导数,尝试发现规律:
兔兔在这里以几个例子说明。
例1:求f(x)=ax 的导数。a是常数。
很显然,导数就是a。
例2:求![]() 的导数,其中a是常数,
的导数,其中a是常数,![]() 。
。
很显然,它是由向量映射向量,对应(5)。求导是向量对向量求导。按分子分布,就是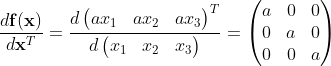 。
。
例3:求![]() 的导数,其中
的导数,其中![]() ,a1,a2,a3是常数。
,a1,a2,a3是常数。![]() 。
。
可以看出,它是把向量映射成数,对应(2)。按分母布局(分母x是列向量形式)计算,就是
可以看出,它是把向量映射成向量。对应(5)。可以按分子布局求导(Ax是列向量,对![]() 求导),就是
求导),就是。
这个是把矩阵映射矩阵,对应(9)。把F(X)堆栈化得![]() ,X堆栈化得
,X堆栈化得![]() 。按分子布局,求导后就是
。按分子布局,求导后就是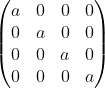 。可以尝试,分母布局计算也是这个结果的。
。可以尝试,分母布局计算也是这个结果的。
这个是把矩阵映射成行向量。按照分母分布计算导数,结果就是 。若按照分子分布,结果就是分母分布的转置:
。若按照分子分布,结果就是分母分布的转置:![]() 。
。
到这里同学们应该已经知道如何计算了,把函数和变元都堆栈化,然后求导。按分子布局,我们发现是![]() ,分母布局是
,分母布局是![]() 。和6的结论是一致的。
。和6的结论是一致的。
此时同学们应该发现其中的规律了,无论是矩阵还是向量还是数,他们求导后都显示出与我们曾经的一元函数求导有着很相似的地方——曾经一元的![]() ,当把a和x分别变成向量、矩阵,也是有着类似的形式。那么对于复杂的函数呢?比如
,当把a和x分别变成向量、矩阵,也是有着类似的形式。那么对于复杂的函数呢?比如![]() 的导数,
的导数,![]() 对x或
对x或![]() 的导数呢。我们用这种方法显然就麻烦许多。那么有没有像我们曾经学过的求导法则一样,针对这一类函数的求导方法呢?答案是肯定的。
的导数呢。我们用这种方法显然就麻烦许多。那么有没有像我们曾经学过的求导法则一样,针对这一类函数的求导方法呢?答案是肯定的。
四:矩阵求导的通用方法。
兔兔在讲公式之前先补充一些知识点。
(1)矩阵的的迹(trace)
![]() 的方阵A的主对角线之和就是矩阵A的迹,记作tr(A)。
的方阵A的主对角线之和就是矩阵A的迹,记作tr(A)。
![]()
性质:(重点,之后会用到的)
![]() ,即线性性质.
,即线性性质.
![]()
![]()
![]() :就是把其中相邻两个看作整体,与第三个做交换,本质就是上一条结论
:就是把其中相邻两个看作整体,与第三个做交换,本质就是上一条结论
对于![]() 和
和![]() ,
,![]() :就是两个矩阵对应位置相乘求和。对于里面
:就是两个矩阵对应位置相乘求和。对于里面![]() 我们也是可以用转置、交换律的,结果不变。
我们也是可以用转置、交换律的,结果不变。
(2)微分
微分只要掌握高数里面那些知识就足够了。这里用到了微分的一些性质。
微分性质:(重点)
![]() , c可以是常数、常向量、常矩阵。
, c可以是常数、常向量、常矩阵。
![]() :即线性性质,与迹相同,u,v可以是一元函数f,也可以是f,F。
:即线性性质,与迹相同,u,v可以是一元函数f,也可以是f,F。
![]() :注意:对于向量或矩阵不可以随便交换乘积先后顺序,他们是不满足交换律的。
:注意:对于向量或矩阵不可以随便交换乘积先后顺序,他们是不满足交换律的。
d(uvw)=d(u)vw+ud(v)w+uvd(w):上面的推广,多个函数乘积也是如此。u、v、w可以是f,F。
![]() :转置性质,与迹的性质相同。
:转置性质,与迹的性质相同。
![]()
![]() ,F为
,F为![]() 维。
维。
矩阵微分:
大概了解一下微分过程与微分形式,后面几条需要记一下。
![]() :A,B是常数阵,微分是零矩阵。
:A,B是常数阵,微分是零矩阵。
![]() :按第一行展开,即元素乘代数余子式,求偏导即可。
:按第一行展开,即元素乘代数余子式,求偏导即可。
![]() 。
。
![]() :X是
:X是![]() 方阵。用
方阵。用![]() ,两边微分移项即可。
,两边微分移项即可。
![]()
我们看到上面的几个情况,不难发现,函数微分等于函数对变元导数乘变元的微分(变元的微分就是按原来的形式把里面xi或xij都变成dxi或dxij)。有时外面加上tr也是成立的。
矩阵微分与导数关系:
这里就是本次矩阵导数的重点结论:
用类似这样形式的式子就可以通过微分来求矩阵导数啦。但对于F,我们可以求tr(F(X))的对X或![]() 导数。
导数。
举例(这里式子很长,兔兔就用纸质书写推导了):
![]()
同学们要注意一下数学矩阵论中的矩阵函数:它和我们这里其实还是很不一样的。那里的矩阵函数是把函数展开成幂级数进行计算的。而我们在深度学习或机器学习过程中,往往是函数作用与向量或矩阵中的每一个元素。而这两种操作结果是完全不一样的。比如对于![]() 当A=
当A=![]() 。用幂级数去计算。
。用幂级数去计算。
import numpy as np
from math import factorial
A=np.mat([[1,2],[3,4]])
s=np.zeros((2,2))
for i in range(10):
s+=A**i/factorial(i) #求级数,先求前十项
print(s) #按数学中矩阵函数的方法求解
print(np.exp(A)) #按机器学习中常用的方法,即对每个元素操作求解运行结果
s=[[ 49.52944224 71.18115079]
[106.77172619 156.30116843]]
exp(A)=[[ 2.71828183 7.3890561 ]
[20.08553692 54.59815003]]可见的确是不一样的,它们也似乎没有什么太大的关联。而在矩阵论中关于矩阵函数乘积的求导,也有着它的定义,它的导数公式是![]() 。它理论应该可以用于咱们这里两个实矩阵函数乘积对变元矩阵的求导,但是它这里由于导数定义和咱们这里有一些区别,所以这个式子应该也是需要调整的,感兴趣的同学可以试一下。
。它理论应该可以用于咱们这里两个实矩阵函数乘积对变元矩阵的求导,但是它这里由于导数定义和咱们这里有一些区别,所以这个式子应该也是需要调整的,感兴趣的同学可以试一下。
五:总结
我们通过了解函数与变元的形式以及导数的定义,知道了这些导数的形式,并且掌握用微分方法求一般的矩阵导数。以上内容虽多,但真正运用的时候应该还是仅仅其中几个。而且在一般模型的推导中,例如BP神经网络的反向传递公式的推导,里面还涉及了很多东西,与今天所讲的矩阵导数可能还是有一定区别,到时候兔兔会详细讲解的。总之,同学们还是需要抓住本质,从根本上去理解。