从DQN到Double DQN和Dueling DQN——pytorch实操
文章目录
- DQN
-
- 直接代码附上
- 为什么会有改进
-
- Double DQN
-
- 代码附上
- Dueling DQN
-
- 话不多说直接给代码
- 改进究竟管用与否?
写这个文章的动机是一直没有人讲明白三种DQN之间的关系,要不过于学术,要不过于工业界。本文试图两方面结合,说说改了什么,有什么好处,效果如何。当然,也是干货满满,直接上代码。
听说点进蝈仔帖子的都喜欢点赞加关注~~
鸣谢:
李宏毅教授 http://speech.ee.ntu.edu.tw/~tlkagk/index.html
深度强化学习中文版一书
知乎专栏:
https://zhuanlan.zhihu.com/p/131662954
DQN
首先附上难得的中文算法表

原理这边简单带过:
先是Q-learning

之后使用网络价值函数逼近:

说白了就是个网络拟合
直接代码附上
这是最经典的小摆锤
# -*- coding: utf-8 -*-
# import the necessary packages
import torch
import torch.nn as nn
from torch.autograd import Variable
import torch.nn.functional as F
import numpy as np
import gym
# 1. Define some Hyper Parameters
BATCH_SIZE = 32 # batch size of sampling process from buffer
LR = 0.01 # learning rate
EPSILON = 0.9 # epsilon used for epsilon greedy approach
GAMMA = 0.9 # discount factor
TARGET_NETWORK_REPLACE_FREQ = 100 # How frequently target netowrk updates
MEMORY_CAPACITY = 2000 # The capacity of experience replay buffer
env = gym.make("CartPole-v0") # Use cartpole game as environment
env = env.unwrapped
N_ACTIONS = env.action_space.n # 2 actions
N_STATES = env.observation_space.shape[0] # 4 states
ENV_A_SHAPE = 0 if isinstance(env.action_space.sample(), int) else env.action_space.sample().shape # to confirm the shape
# 2. Define the network used in both target net and the net for training
class Net(nn.Module):
def __init__(self):
# Define the network structure, a very simple fully connected network
super(Net, self).__init__()
# Define the structure of fully connected network
self.fc1 = nn.Linear(N_STATES, 10) # layer 1
self.fc1.weight.data.normal_(0, 0.1) # in-place initilization of weights of fc1
self.out = nn.Linear(10, N_ACTIONS) # layer 2
self.out.weight.data.normal_(0, 0.1) # in-place initilization of weights of fc2
def forward(self, x):
# Define how the input data pass inside the network
x = self.fc1(x)
x = F.relu(x)
actions_value = self.out(x)
return actions_value
# 3. Define the DQN network and its corresponding methods
class DQN(object):
def __init__(self):
# -----------Define 2 networks (target and training)------#
self.eval_net, self.target_net = Net(), Net()
# Define counter, memory size and loss function
self.learn_step_counter = 0 # count the steps of learning process
self.memory_counter = 0 # counter used for experience replay buffer
# ----Define the memory (or the buffer), allocate some space to it. The number
# of columns depends on 4 elements, s, a, r, s_, the total is N_STATES*2 + 2---#
self.memory = np.zeros((MEMORY_CAPACITY, N_STATES * 2 + 2))
#------- Define the optimizer------#
self.optimizer = torch.optim.Adam(self.eval_net.parameters(), lr=LR)
# ------Define the loss function-----#
self.loss_func = nn.MSELoss()
def choose_action(self, x):
# This function is used to make decision based upon epsilon greedy
x = torch.unsqueeze(torch.FloatTensor(x), 0) # add 1 dimension to input state x
# input only one sample
if np.random.uniform() < EPSILON: # greedy
# use epsilon-greedy approach to take action
actions_value = self.eval_net.forward(x)
#print(torch.max(actions_value, 1))
# torch.max() returns a tensor composed of max value along the axis=dim and corresponding index
# what we need is the index in this function, representing the action of cart.
action = torch.max(actions_value, 1)[1].data.numpy()
action = action[0] if ENV_A_SHAPE == 0 else action.reshape(ENV_A_SHAPE) # return the argmax index
else: # random
action = np.random.randint(0, N_ACTIONS)
action = action if ENV_A_SHAPE == 0 else action.reshape(ENV_A_SHAPE)
return action
def store_transition(self, s, a, r, s_):
# This function acts as experience replay buffer
transition = np.hstack((s, [a, r], s_)) # horizontally stack these vectors
# if the capacity is full, then use index to replace the old memory with new one
index = self.memory_counter % MEMORY_CAPACITY
self.memory[index, :] = transition
self.memory_counter += 1
def learn(self):
# Define how the whole DQN works including sampling batch of experiences,
# when and how to update parameters of target network, and how to implement
# backward propagation.
# update the target network every fixed steps
if self.learn_step_counter % TARGET_NETWORK_REPLACE_FREQ == 0:
# Assign the parameters of eval_net to target_net
self.target_net.load_state_dict(self.eval_net.state_dict())
self.learn_step_counter += 1
# Determine the index of Sampled batch from buffer
sample_index = np.random.choice(MEMORY_CAPACITY, BATCH_SIZE) # randomly select some data from buffer
# extract experiences of batch size from buffer.
b_memory = self.memory[sample_index, :]
# extract vectors or matrices s,a,r,s_ from batch memory and convert these to torch Variables
# that are convenient to back propagation
b_s = Variable(torch.FloatTensor(b_memory[:, :N_STATES]))
# convert long int type to tensor
b_a = Variable(torch.LongTensor(b_memory[:, N_STATES:N_STATES+1].astype(int)))
b_r = Variable(torch.FloatTensor(b_memory[:, N_STATES+1:N_STATES+2]))
b_s_ = Variable(torch.FloatTensor(b_memory[:, -N_STATES:]))
# calculate the Q value of state-action pair
q_eval = self.eval_net(b_s).gather(1, b_a) # (batch_size, 1)
#print(q_eval)
# calculate the q value of next state
q_next = self.target_net(b_s_).detach() # detach from computational graph, don't back propagate
# select the maximum q value
#print(q_next)
# q_next.max(1) returns the max value along the axis=1 and its corresponding index
q_target = b_r + GAMMA * q_next.max(1)[0].view(BATCH_SIZE, 1) # (batch_size, 1)
loss = self.loss_func(q_eval, q_target)
self.optimizer.zero_grad() # reset the gradient to zero
loss.backward()
self.optimizer.step() # execute back propagation for one step
'''
--------------Procedures of DQN Algorithm------------------
'''
# create the object of DQN class
dqn = DQN()
# Start training
print("\nCollecting experience...")
for i_episode in range(400):
# play 400 episodes of cartpole game
s = env.reset()
ep_r = 0
while True:
env.render()
# take action based on the current state
a = dqn.choose_action(s)
# obtain the reward and next state and some other information
s_, r, done, info = env.step(a)
# modify the reward based on the environment state
x, x_dot, theta, theta_dot = s_
r1 = (env.x_threshold - abs(x)) / env.x_threshold - 0.8
r2 = (env.theta_threshold_radians - abs(theta)) / env.theta_threshold_radians - 0.5
r = r1 + r2
# store the transitions of states
dqn.store_transition(s, a, r, s_)
ep_r += r
# if the experience repaly buffer is filled, DQN begins to learn or update
# its parameters.
if dqn.memory_counter > MEMORY_CAPACITY:
dqn.learn()
if done:
print('Ep: ', i_episode, ' |', 'Ep_r: ', round(ep_r, 2))
if done:
# if game is over, then skip the while loop.
break
# use next state to update the current state.
s = s_
为什么会有改进
DQN的实践过程中会出现一些问题,比如高估了动作值(overestimation)。
Double DQN
Double DQN其实就是Double Q learning在DQN上的拓展,上面Q和Q2两套Q值,分别对应DQN的policy network(更新的快)和target network(每隔一段时间与policy network同步)。
换言之:
Double DQN(DDQN)是DQN的一种改进。在DDQN之前,基本所有的目标Q值都是通过贪婪法得到的,而这往往会造成过度估计(overestimations)的问题。DDQN将目标Q值的最大动作分解成动作选择和动作评估两步,有效解决了这个问题。
Double Q learning error如下:

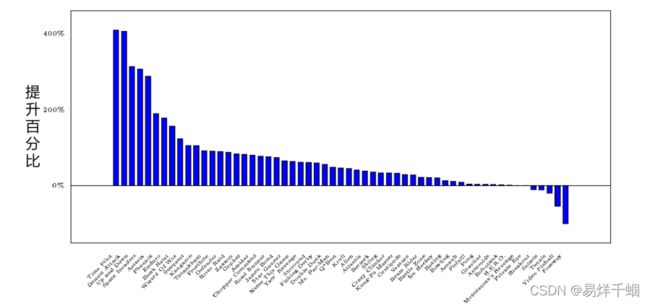
Double DQN 相比于 DQN 的效果提升情况如图

代码附上
实现起来也很简单,只需要在DQN计算TD error的时候稍作改动:
def compute_td_loss(self, states, actions, rewards, next_states, is_done, gamma=0.99):
""" Compute td loss using torch operations only. Use the formula above. """
actions = torch.tensor(actions).long() # shape: [batch_size]
rewards = torch.tensor(rewards, dtype =torch.float) # shape: [batch_size]
is_done = torch.tensor(done).bool() # shape: [batch_size]
if self.USE_CUDA:
actions = actions.cuda()
rewards = rewards.cuda()
is_done = is_done.cuda()
# get q-values for all actions in current states
predicted_qvalues = self.DQN(states)
# select q-values for chosen actions
predicted_qvalues_for_actions = predicted_qvalues[
range(states.shape[0]), actions
]
# compute q-values for all actions in next states
## Where DDQN is different from DQN
predicted_next_qvalues_current = self.DQN(next_states)
predicted_next_qvalues_target = self.DQN_target(next_states)
# compute V*(next_states) using predicted next q-values
next_state_values = predicted_next_qvalues_target.gather(1, torch.max(predicted_next_qvalues_current, 1)[1].unsqueeze(1)).squeeze(1)
# compute "target q-values" for loss - it's what's inside square parentheses in the above formula.
target_qvalues_for_actions = rewards + gamma *next_state_values # YOUR CODE
# at the last state we shall use simplified formula: Q(s,a) = r(s,a) since s' doesn't exist
target_qvalues_for_actions = torch.where(
is_done, rewards, target_qvalues_for_actions)
# mean squared error loss to minimize
#loss = torch.mean((predicted_qvalues_for_actions -
# target_qvalues_for_actions.detach()) ** 2)
loss = F.smooth_l1_loss(predicted_qvalues_for_actions, target_qvalues_for_actions.detach())
return loss
Dueling DQN
话不多说直接给代码
Dueling DQN在DQN上的修改也很小,只是多出一支fully connected layer来估计V(s)。代码如下:
class Dueling_DQN(nn.Module):
def __init__(self, input_shape, num_outputs):
super(Dueling_DQN, self).__init__()
self.input_shape = input_shape
self.num_actions = num_outputs
self.features = nn.Sequential(
nn.Conv2d(input_shape[0], 32, kernel_size=8, stride=4),
nn.ReLU(),
nn.Conv2d(32, 64, kernel_size=4, stride=2),
nn.ReLU(),
nn.Conv2d(64, 64, kernel_size=3, stride=1),
nn.ReLU()
)
self.advantage = nn.Sequential(
nn.Linear(self.feature_size(), 512),
nn.ReLU(),
nn.Linear(512, num_outputs)
)
self.value = nn.Sequential(
nn.Linear(self.feature_size(), 512),
nn.ReLU(),
nn.Linear(512, 1)
)
def forward(self, x):
x = self.features(x)
x = x.view(x.size(0), -1)
advantage = self.advantage(x)
value = self.value(x)
return value + advantage - advantage.mean()
def feature_size(self):
return self.features(autograd.Variable(torch.zeros(1, *self.input_shape))).view(1, -1).size(1)
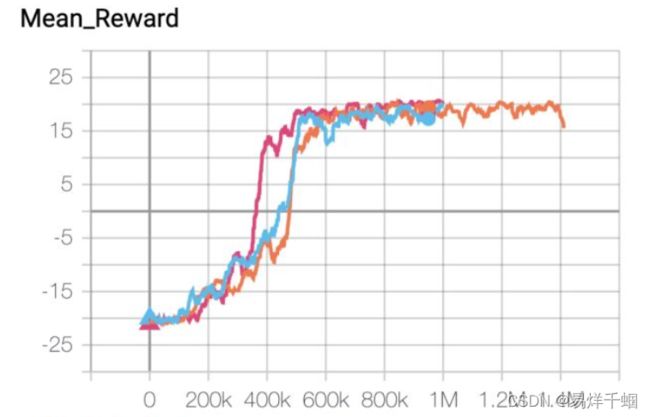
改进究竟管用与否?
下面是DDQN(蓝色),Dueling DQN(粉红)和DQN(橘黄)在Pong上面得表现。可以看到DDQN > Dueling DQN > DQN,其中DDQN大约比DQN得收敛快10%。