主成分分析——PCA
主成分分析是一种降维算法，它能将多个指标转换为少数几个主成分，这些主成分是原始变量的线性组合，且彼此之间互不相关，其能反映出原始数据的大部分信息。一般来说，当研究的问题涉及到多变量且变量之间存在很强的相关性时，我们可考虑使用主成分分析的方法来对数据进行简化。
目录
前言
一、PCA
1，PCA的思想
2，算法流程：
1，我们首先对其进行标准化处理:
2，计算标准化样本得协方差矩阵
3，计算R的特征值和特征向量
4，计算主成分贡献率以及累计贡献率
5，写出主成分
6，根据系数分析主成分代表的意义
3，演示一波
二、题目知识点复习
1，eg1
2，eg2
3，eg3
4，eg4
三，sklearn的PCA使用
前言
一、PCA
1，PCA的思想
假设有
个样本，
个指标，则可构成大小为
的样本矩阵
:
假设我们想找到新的一组变量
,且他们满足：
系数
的确定原则：
1）
与
相互无关；
2）
与
的一切线性组合中方差最大者；
3）
是与不相关的的所有线性组合中方差最大者；
4）依次推断，
是与
不相关的的所有线性组合中方差最大者
5）新变量指标
,分别称为原变量指标的第一，第二，
,第m主成分
2，算法流程：
假设有个样本，个指标，则可构成大小为的样本矩阵:
1，我们首先对其进行标准化处理:
按列计算均值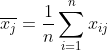
和标准差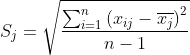
，计算得标准化数据
，原始样本矩阵经过标准化变为：
2，计算标准化样本得协方差矩阵
其中
（上面两步等同于算皮尔曼相关系数矩阵）
3，计算R的特征值和特征向量
特征值：
(R是半正定矩阵，且
）
特征向量：
4，计算主成分贡献率以及累计贡献率
贡献率：
累计贡献率：
5，写出主成分
一般取累计贡献率超过80%的特征值所对应的第一、第二、 ,第
个主成分。第 i 个主成分：
6，根据系数分析主成分代表的意义
对于某个主成分而言，指标前面的系数越大，代表该指标对于该主成分的影响越大。
3，演示一波
利用 鸢尾花数据
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data
y = iris.target
n = X.shape[0]
print(n)1，标准化——去除量纲影响
from sklearn.preprocessing import StandardScaler
std = StandardScaler()
X = std.fit_transform(X)
2，计算协方差
X_bar = X.mean(axis=0)#均值
Xp = X - X_bar
Cov = Xp.T.dot(Xp)/n 
（这个矩阵就是皮尔逊相关矩阵其实）
3，计算特征值与特征向量
a, b = np.linalg.eig(Cov) #特征值赋值给a，对应特征向量赋值给b 
4，贡献率与累计贡献率
#贡献率
contributes = a/a.sum()
#累计贡献率
contributes_rate = contributes.copy()
for i in range(1, len(contributes)):
contributes_rate[i] += contributes_rate[i-1]
5，取出最大的k个特征向量
selected = b[:, :k]
new_X = X.dot(selected)二、题目知识点复习
1，eg1
记住为什么求协方差，求协方差就是为了求指标与指标之间的相关性，如热力图
都是两两指标的比较。所以协方差矩阵大小一定是（指标*指标） 的
这里每个样本都是k维，那么就是样本指标大小为k，那就是k*k
选D
2，eg2
求协方差要先求样本均值，然后再根据公式进行矩阵乘法
选B
3，eg3
不管是matlab还python都是eig
选D
4，eg4
只要
就可达到累计贡献率90%
选ACD
三，sklearn的PCA使用
按建模理论来说，PCA一定要先标准化再调用PCA，这里我用了通道法进行封装两个模型
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris
from sklearn.pipeline import Pipeline
iris = load_iris()
n_components = 2 # 将减少后的维度设置为2
model = Pipeline([
('ss', StandardScaler()),
('md', PCA(n_components=n_components)),
])
model = model.fit(iris.data)
new_data = model.transform(iris.data) # 变换后的数据