手推支持向量机SVM——Ⅰ
支持向量机的原理
首先,我们要知道,SVM是一个二分类模型,当然我们能够用它实现多分类,但一个SVM本质上就只是一个二分类模型,它的原理就是找到一个超平面(在二维中就是一条直线)既能有效区分两个类别又能使得两个类别到该超平面的几何距离最大。
什么意思呢,看下面的图:
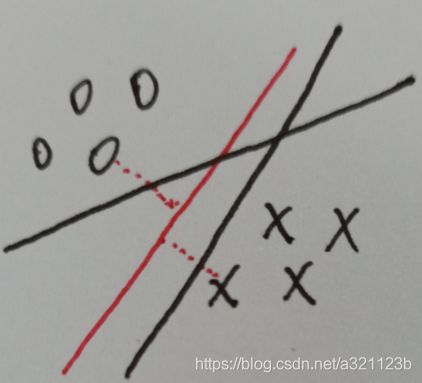
该图中有很明显的两个类别,能够区分开这两个类别的直线有很多条(图中的三条直线都可以),SVM要做的就是找到离两个类别的距离最远的那一条,即图中的红色直线。
目前共有三种SVM算法:
- Hard-margin SVM 硬间隔SVM
- Soft-margin SVM 软间隔SVM
- Kernel SVM 带核函数的SVM
下面就一一进行讲解。
Hard-margin SVM
我们通常说的SVM都指的是Hard-margin SVM,其中的hard表示的是不允许误差,这是有别于sotf-margin的一点,后面再详细讲解。
首先,我们将SVM分类器定义为:
{ w T x i + b > 0 , y i = 1 w T x i + b < 0 , y i = − 1 \begin{cases}w^{T}x_{i}+b >0,y_{i}=1\\ w^{T}x_{i}+b <0,y_{i}=-1\end{cases} {wTxi+b>0,yi=1wTxi+b<0,yi=−1
其中, w T x i + b w^{T}x_{i}+b wTxi+b为我们找到的直线,则直线上方为正类即 y i = 1 y_{i}=1 yi=1,直线下方为负类即 y i = − 1 y_{i}=-1 yi=−1。
不难看出上式等价于:
y i ( w T x i + b ) > 0 y_{i}(w^{T}x_{i}+b) >0 yi(wTxi+b)>0
样本中的点到直线的最小距离为:
m a r g i n = m i n d i s t a n c e ( w , b , x i ) margin=min\ distance(w,b,x_{i}) margin=min distance(w,b,xi)
代入点到直线的距离公式,得:
m a r g i n = m i n 1 ∣ ∣ w ∣ ∣ 2 ∙ ∣ w T x i + b ∣ margin=min\ \frac{1}{||w||_{2}}\bullet |w^{T}x_{i}+b| margin=min ∣∣w∣∣21∙∣wTxi+b∣
其中 ∣ ∣ w ∣ ∣ 2 ||w||_{2} ∣∣w∣∣2为L2范数。
∣ ∣ w ∣ ∣ 2 = w 1 2 + w 2 2 + . . . + w n 2 ||w||_{2}=\sqrt{w_{1}^{2}+w_{2}^{2}+...+w_{n}^{2}} ∣∣w∣∣2=w12+w22+...+wn2
然后hard-margin SVM的目标就是使该最小距离最大化,即:
{ m a x m i n 1 ∣ ∣ w ∣ ∣ 2 ∙ ∣ w T x i + b ∣ y i ( w T x i + b ) > 0 \begin{cases}max \ min\ \frac{1}{||w||_{2}}\bullet |w^{T}x_{i}+b|\\ y_{i}(w^{T}x_{i}+b) >0\end{cases} {max min ∣∣w∣∣21∙∣wTxi+b∣yi(wTxi+b)>0
由 y i ∈ { − 1 , 1 } y_{i}\in \begin{Bmatrix}-1,1 \end{Bmatrix} yi∈{−1,1}且与 w T x i + b w^{T}x_{i}+b wTxi+b同号,因此我们可以去掉绝对值符号。得:
{ m a x m i n 1 ∣ ∣ w ∣ ∣ 2 ∙ y i ( w T x i + b ) y i ( w T x i + b ) > 0 \begin{cases}max \ min\ \frac{1}{||w||_{2}}\bullet y_{i}(w^{T}x_{i}+b)\\ y_{i}(w^{T}x_{i}+b) >0\end{cases} {max min ∣∣w∣∣21∙yi(wTxi+b)yi(wTxi+b)>0
将常数项提出来,得:
{ m a x 1 ∣ ∣ w ∣ ∣ 2 m i n y i ( w T x i + b ) y i ( w T x i + b ) > 0 \begin{cases}max \frac{1}{||w||_{2}}\ min\ y_{i}(w^{T}x_{i}+b)\\ y_{i}(w^{T}x_{i}+b) >0\end{cases} {max∣∣w∣∣21 min yi(wTxi+b)yi(wTxi+b)>0
由 y i ( w T x i + b ) > 0 y_{i}(w^{T}x_{i}+b) >0 yi(wTxi+b)>0可知,一定存在 r > 1 r>1 r>1,使得 m i n y i ( w T x i + b ) = r min\ y_{i}(w^{T}x_{i}+b)=r min yi(wTxi+b)=r,令 r = 1 r=1 r=1,则上式变为:
{ m a x 1 ∣ ∣ w ∣ ∣ 2 m i n y i ( w T x i + b ) = 1 \begin{cases}max \frac{1}{||w||_{2}}\ \\ min\ y_{i}(w^{T}x_{i}+b)=1\end{cases} {max∣∣w∣∣21 min yi(wTxi+b)=1
=> { m a x 1 ∣ ∣ w ∣ ∣ 2 m i n y i ( w T x i + b ) = 1 \begin{cases}max \frac{1}{||w||_{2}}\ \\ min\ y_{i}(w^{T}x_{i}+b)=1\end{cases} {max∣∣w∣∣21 min yi(wTxi+b)=1
将max问题转换为min问题:
{ m i n 1 2 w T w y i ( w T x i + b ) ⩾ 1 , i = 1 , 2 , . . . N \begin{cases}min \frac{1}{2}w^{T}w\ \\ \ y_{i}(w^{T}x_{i}+b)\geqslant 1 \ \ ,i=1,2,...N\end{cases} {min21wTw yi(wTxi+b)⩾1 ,i=1,2,...N
解释一下最后一步,这里的 m i n ∣ ∣ w ∣ ∣ 2 = m i n w T w min||w||_{2}=min \ w^{T}w min∣∣w∣∣2=min wTw应该不难理解,主要是这个 1 2 \frac{1}{2} 21怎么来的,其一是因为乘一个常数项并不影响求最优值,其二是为了方便后面的求导运算。
于是我们就得到了带N个约束条件的求二次函数的最值问题或者说是凸函数的优化问题了,上面标红的公式就是大名鼎鼎的SVM的原问题了。
容易看出,原问题的求解与特征的维数有关,当特征维数较高时我们很难进行求解,因此我们将其转换为对偶问题。
首先,通过构造拉格朗日函数将约束条件消除。原问题中的约束条件可以写成:
1 − y i ( w T x i + b ) ⩽ 0 1-y_{i}(w^{T}x_{i}+b) \leqslant 0 1−yi(wTxi+b)⩽0
然后,构造拉格朗日函数:
L ( w , b , λ ) = 1 2 w T w + ∑ i = 1 N λ i [ 1 − y i ( w T x i + b ) ] L(w,b,\lambda)= \frac{1}{2}w^{T}w + \sum_{i=1}^{N}\lambda _{i}[1-y_{i}(w^{T}x_{i}+b)] L(w,b,λ)=21wTw+i=1∑Nλi[1−yi(wTxi+b)]
其中, λ \lambda λ为拉格朗日系数,且 λ i ⩾ 0 \lambda _{i}\geqslant 0 λi⩾0, 1 − y i ( w T x i + b ) ⩽ 0 1-y_{i}(w^{T}x_{i}+b) \leqslant 0 1−yi(wTxi+b)⩽0
则,原问题 m i n 1 2 w T w min \frac{1}{2}w^{T}w min21wTw可以转换为 m i n [ m a x L ( w , b , λ ) ] min[max \ L(w,b,\lambda)] min[max L(w,b,λ)],why?
从两个方面来看:
①在可行解区域内,满足 1 − y i ( w T x i + b ) ⩽ 0 1-y_{i}(w^{T}x_{i}+b) \leqslant 0 1−yi(wTxi+b)⩽0,即 m a x L ( w , b , λ ) = 1 2 w T w max \ L(w,b,\lambda)=\frac{1}{2}w^{T}w max L(w,b,λ)=21wTw,因为 L ( w , b , λ ) L(w,b,\lambda) L(w,b,λ)第二部分的最大值为0;
②在可行解区域外,即 1 − y i ( w T x i + b ) > 0 1-y_{i}(w^{T}x_{i}+b) > 0 1−yi(wTxi+b)>0 且 λ i ⩾ 0 \lambda _{i}\geqslant 0 λi⩾0,则 m a x L ( w , b , λ ) = + ∞ max \ L(w,b,\lambda)= + \infty max L(w,b,λ)=+∞,无解,而原问题同样在可行解区域外。
结合①②可知, m i n 1 2 w T w min \frac{1}{2}w^{T}w min21wTw等价于 m i n [ m a x L ( w , b , λ ) ] min[max \ L(w,b,\lambda)] min[max L(w,b,λ)],从而,带约束的原问题转换成了无约束的:
{ m i n m a x L ( w , b , λ ) λ i ⩾ 0 \left\{\begin{matrix}min \ max \ L(w,b,\lambda ) & \\ \lambda _{i}\geqslant 0& \end{matrix}\right. {min max L(w,b,λ)λi⩾0
然后,我们来说一下什么是对偶性。
- 弱对偶性: m i n m a x f ( x ) ⩾ m a x m i n f ( x ) min \ max \ f(x) \geqslant max\ min\ f(x) min max f(x)⩾max min f(x)
- 强对偶性: m i n m a x f ( x ) = m a x m i n f ( x ) min \ max \ f(x) = max\ min\ f(x) min max f(x)=max min f(x)
在SVM中,满足强对偶性的充要条件是满足KKT条件,如下:
{ ∂ L ∂ b = 0 , ∂ L ∂ w = 0 , ∂ L ∂ λ = 0 λ i ( 1 − y i ( w T x i + b ) ) = 0 1 − y i ( w T x i + b ) ⩽ 0 λ i ⩾ 0 \left\{\begin{matrix}\frac{\partial L}{\partial b}=0,\frac{\partial L}{\partial w}=0,\frac{\partial L}{\partial \lambda}=0 \\ \lambda_{i}(1-y_{i}(w^{T}x_{i}+b))=0 \\ 1-y_{i}(w^{T}x_{i}+b)\leqslant 0 \\ \lambda _{i}\geqslant 0 \end{matrix}\right. ⎩⎪⎪⎨⎪⎪⎧∂b∂L=0,∂w∂L=0,∂λ∂L=0λi(1−yi(wTxi+b))=01−yi(wTxi+b)⩽0λi⩾0
其中, λ i ( 1 − y i ( w T x i + b ) ) = 0 \lambda_{i}(1-y_{i}(w^{T}x_{i}+b))=0 λi(1−yi(wTxi+b))=0称为松弛互补条件。
当满足KKT条件后,我们就可以把原问题转换为对偶问题了,即:
{ m i n m a x L ( w , b , λ ) λ i ⩾ 0 = { m a x m i n L ( w , b , λ ) λ i ⩾ 0 \left\{\begin{matrix}min \ max \ L(w,b,\lambda ) & \\ \lambda _{i}\geqslant 0& \end{matrix}\right.=\left\{\begin{matrix}max\ min\ L(w,b,\lambda ) & \\ \lambda _{i}\geqslant 0& \end{matrix}\right. {min max L(w,b,λ)λi⩾0={max min L(w,b,λ)λi⩾0
下面我们来求 m i n L ( w , b , λ ) min \ L(w,b,\lambda) min L(w,b,λ)。
由
∂ L ∂ b = 0 ⇒ − ∑ i = 1 N λ i y i = 0 ⇒ ∑ i = 1 N λ i y i = 0 \frac{\partial L}{\partial b}=0 \ \Rightarrow -\sum_{i=1}^{N}\lambda _{i}y_{i}=0 \ \Rightarrow \sum_{i=1}^{N}\lambda _{i}y_{i}=0 ∂b∂L=0 ⇒−∑i=1Nλiyi=0 ⇒∑i=1Nλiyi=0
展开 L ( w , b , λ ) L(w,b,\lambda) L(w,b,λ):
L ( w , b , λ ) = 1 2 w T w + ∑ i = 1 N λ i − ∑ i = 1 N λ i y i w T x i − b ∑ i = 1 N λ i y i L(w,b,\lambda)= \frac{1}{2}w^{T}w + \sum_{i=1}^{N}\lambda _{i}-\sum_{i=1}^{N}\lambda _{i}y_{i}w^{T}x_{i}-b \sum_{i=1}^{N}\lambda _{i}y_{i}\textup{} L(w,b,λ)=21wTw+i=1∑Nλi−i=1∑NλiyiwTxi−bi=1∑Nλiyi
=>
L ( w , b , λ ) = 1 2 w T w + ∑ i = 1 N λ i − ∑ i = 1 N λ i y i w T x i L(w,b,\lambda)= \frac{1}{2}w^{T}w + \sum_{i=1}^{N}\lambda _{i}-\sum_{i=1}^{N}\lambda _{i}y_{i}w^{T}x_{i} L(w,b,λ)=21wTw+i=1∑Nλi−i=1∑NλiyiwTxi
由 ∂ L ∂ w = 0 ⇒ 1 2 ∗ 2 ∗ w − ∑ i = 1 N λ i y i x i = 0 \frac{\partial L}{\partial w}=0 \ \Rightarrow \frac{1}{2}*2*w-\sum_{i=1}^{N}\lambda _{i}y_{i}x_{i}=0 ∂w∂L=0 ⇒21∗2∗w−∑i=1Nλiyixi=0,可得:
w = ∑ i = 1 N λ i y i x i w=\sum_{i=1}^{N}\lambda _{i}y_{i}x_{i} w=i=1∑Nλiyixi
代入 L ( w , b , λ ) L(w,b,\lambda) L(w,b,λ),得:
L ( w , b , λ ) = 1 2 ( ∑ i = 1 N λ i y i x i ) T ( ∑ i = 1 N λ i y i x i ) + ∑ i = 1 N λ i − ( ∑ i = 1 N λ i y i x i ) T ( ∑ i = 1 N λ i y i x i ) L(w,b,\lambda)=\frac{1}{2}(\sum_{i=1}^{N}\lambda _{i}y_{i}x_{i})^{T}(\sum_{i=1}^{N}\lambda _{i}y_{i}x_{i})+\sum_{i=1}^{N}\lambda _{i}-(\sum_{i=1}^{N}\lambda _{i}y_{i}x_{i})^{T}(\sum_{i=1}^{N}\lambda _{i}y_{i}x_{i}) L(w,b,λ)=21(i=1∑Nλiyixi)T(i=1∑Nλiyixi)+i=1∑Nλi−(i=1∑Nλiyixi)T(i=1∑Nλiyixi)
=>
L ( w , b , λ ) = ∑ i = 1 N λ i − 1 2 ( ∑ i = 1 N λ i y i x i ) T ( ∑ i = 1 N λ i y i x i ) L(w,b,\lambda)=\sum_{i=1}^{N}\lambda _{i}-\frac{1}{2}(\sum_{i=1}^{N}\lambda _{i}y_{i}x_{i})^{T}(\sum_{i=1}^{N}\lambda _{i}y_{i}x_{i}) L(w,b,λ)=i=1∑Nλi−21(i=1∑Nλiyixi)T(i=1∑Nλiyixi)
=>
L ( w , b , λ ) = ∑ i = 1 N λ i − 1 2 ∑ i = 1 N ∑ j = 1 N λ i λ j y i y j x i T x j L(w,b,\lambda)=\sum_{i=1}^{N}\lambda _{i}-\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\lambda _{i}\lambda _{j}y_{i}y_{j}x_{i}^{T}x_{j} L(w,b,λ)=i=1∑Nλi−21i=1∑Nj=1∑NλiλjyiyjxiTxj
则 { m a x m i n L ( w , b , λ ) λ i ⩾ 0 \left\{\begin{matrix}max\ min\ L(w,b,\lambda ) & \\ \lambda _{i}\geqslant 0& \end{matrix}\right. {max min L(w,b,λ)λi⩾0
转为了:
{ m a x ∑ i = 1 N λ i − 1 2 ∑ i = 1 N ∑ j = 1 N λ i λ j y i y j x i T x j λ i ⩾ 0 \left\{\begin{matrix}max\ \sum_{i=1}^{N}\lambda _{i}-\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\lambda _{i}\lambda _{j}y_{i}y_{j}x_{i}^{T}x_{j} & \\ \lambda _{i}\geqslant 0& \end{matrix}\right. {max ∑i=1Nλi−21∑i=1N∑j=1NλiλjyiyjxiTxjλi⩾0
将max问题转为min问题:
{ m i n 1 2 ∑ i = 1 N ∑ j = 1 N λ i λ j y i y j x i T x j − ∑ i = 1 N λ i λ i ⩾ 0 \left\{\begin{matrix}min\ \frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\lambda _{i}\lambda _{j}y_{i}y_{j}x_{i}^{T}x_{j}-\sum_{i=1}^{N}\lambda _{i} & \\ \lambda _{i}\geqslant 0& \end{matrix}\right. {min 21∑i=1N∑j=1NλiλjyiyjxiTxj−∑i=1Nλiλi⩾0
容易看出,该优化问题只与数据量有关,这就是大名鼎鼎的SVM的对偶问题。
最后,就是如何求解最优的 w ∗ w^{*} w∗和 b ∗ b^{*} b∗:
①由 ∂ L ∂ w = 0 \frac{\partial L}{\partial w}=0 ∂w∂L=0,可得: w ∗ = ∑ i = 1 N λ i y i x i w^{*}=\sum_{i=1}^{N}\lambda _{i}y_{i}x_{i} w∗=∑i=1Nλiyixi;
②由松弛互补条件,当 λ i = 0 \lambda _{i}=0 λi=0时无法求出 b ∗ b^{*} b∗,因此令 1 − y i ( w T x i ) = 0 1-y_{i}(w^{T}x_{i})=0 1−yi(wTxi)=0,即
y i ( w T x i ) = 1 y_{i}(w^{T}x_{i})=1 yi(wTxi)=1
由于 y i = { − 1 , 1 } y_{i}=\begin{Bmatrix}-1,1 \end{Bmatrix} yi={−1,1},两边同乘 y i y_{i} yi,得:
w T x i + b = y i ⇒ b ∗ = y i − w T x i w^{T}x_{i}+b=y_{i}\Rightarrow b^*=y_{i}-w^{T}x_{i} wTxi+b=yi⇒b∗=yi−wTxi
将 w ∗ w^{*} w∗代入,得:
b ∗ = y i − ( ∑ i = 1 N λ i x i y i ) T x i = y i − ∑ i = 1 N ∑ k = 1 N λ k y k x k T x i b^{*}=y_{i}-(\sum_{i=1}^{N}\lambda_{i}x_{i}y_{i})^{T}x_{i}=y_{i}-\sum_{i=1}^{N}\sum_{k=1}^{N}\lambda_{k}y_{k}x_{k}^{T}x_{i} b∗=yi−(i=1∑Nλixiyi)Txi=yi−i=1∑Nk=1∑NλkykxkTxi
最终找到的SVM表达式为: f ( x ) = s i g n ( w ∗ T x + b ∗ ) f(x)=sign(w^{*^{T}}x+b^{*}) f(x)=sign(w∗Tx+b∗)。
最终找到的最优超平面为: w ∗ T x + b ∗ w^{*^{T}}x+b^{*} w∗Tx+b∗。
最后,为坚持看到这里的你鼓个掌。