机器学习算法 之 支持向量机 SVM
一、 第一次学习
1 基本知识
参考网址:麻省理工学院公开课:人工智能16 学习:支持向量机






2 面试问题
参考书籍:百面机器学习
2.1 问题1
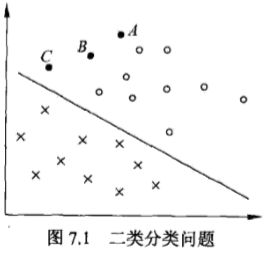
在空间上线性可分的两类点,分别向SVM分类的超平面上做投影,这些点在 超平面上的投影仍然是线性可分的吗?
这里需要用到凸集、凸组合、凸包的概念,可以参考另一篇文章:凸函数与凸规划

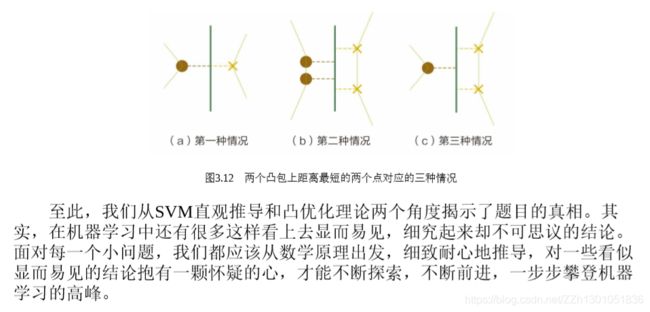
如下,是笔者自己对问题1 的图形化解答,方便理解记忆(可能有点抽象,2333)。

二、第二次学习
参考书籍:《统计学习方法-李航》的支持向量机一章。
本次学习内容为《统计学习方法》中的支持向量机介绍,学习时,先浏览最后的本章概要,再看本章概述,再由简至繁地看三种支持向量机模型。下面也按该顺序进行介绍。
1 本章概要
本章概要中依次总结了硬间隔支持向量机、软间隔支持向量机、非线性支持向量机、SMO算法。
学习时,先浏览概要即可,大体了解本章要学习的内容。
1.1 硬间隔支持向量机
笔者概述:
支持向量机最简单的模型:硬间隔支持向量机。
使用条件:数据线性可分。
学习策略:最大化硬间隔。
原始最优化问题: m i n 1 2 ∣ ∣ w ∣ ∣ 2 min\frac{1}{2}||w||^2 min21∣∣w∣∣2
最优化问题的解: w ∗ w^* w∗, b ∗ b^* b∗
求最优值 w ∗ w^* w∗, b ∗ b^* b∗的方法:先求对偶问题的最优值 α ∗ α^* α∗,再求最优值 w ∗ w^* w∗, b ∗ b^* b∗,得到分离超平面和分类决策函数。
分离超平面: w ∗ x + b ∗ = 0 w^*x+b^*=0 w∗x+b∗=0
分类决策函数: s i g n ( w ∗ x + b ∗ ) sign(w^*x+b^*) sign(w∗x+b∗)
2 支持向量机 概述
2.1 支持向量机 是什么
书籍原文:
补课:凸二次规划
这里只补课凸二次规划,其他不明白的地方,后面会介绍。
参考网址:支持向量机从入门到放弃再到掌握
- 什么是凸?什么是凸优化?
凸优化说的是这么一回事情: X ⊂ R n X\subset R^n X⊂Rn为一凸集, f : X → R f:X \rightarrow R f:X→R为一凸函数,凸优化就是要找出一点 x ∗ ∈ X x^* \in X x∗∈X,使得任意 x ∈ X x \in X x∈X都满足 f ( x ∗ ) ≤ f ( x ) f(x^*) \leq f(x) f(x∗)≤f(x)。
.
可以想象成给我一个凸函数,我要去找到最低点。

- 为啥叫二次规划问题呢?
据了解(其实就是知道),
目标函数和约束条件都为变量的线性函数,叫做-----线性规划问题。
目标函数为变量的二次函数和约束条件为变量的线性函数,叫做-----二次规划问题。
目标函数和约束条件都为非线性函数,叫做-----非线性规划问题。
2.2 支持向量机的三种模型
笔者概述:
支持向量机包含由简至繁的三个模型:
| 数据特点 | 学习方法 | 学习策略 |
|---|---|---|
| 线性可分 | 硬间隔支持向量机 | 最大化硬间隔 |
| 近似线性可分 | 软间隔支持向量机 | 最大化软间隔 |
| 非线性可分 | 非线性支持向量机 | 最大化软间隔+核技巧 |
其中硬间隔支持向量机又叫线性可分支持向量机。
软间隔支持向量机又叫线性支持向量机。
非线性支持向量机就没有别名了。
2.3 核方法
笔者概述:
核函数:向量之间的內积。这里的向量是从输入空间映射到特征空间得到的特征向量。
-
线性空间
线性空间中,向量之间的基本运算为线性运算(加法和数量乘法),其具体模型为几何空间 R 2 R^2 R2、 R 3 R^3 R3… R n R^n Rn,例如:
实数领域的线性运算: 3 + 5 3+5 3+5、 3 x 3x 3x
矩阵的线性运算: A + B A+B A+B、 3 A 3A 3A
向量的线性运算: α ⃗ 1 + α ⃗ 2 \vec α_1 + \vec α_2 α1+α2、 3 α ⃗ 1 3\vec α_1 3α1
.
线性空间=加法+数乘
参考网址:线性运算_百度百科 -
欧式空间
线性空间的不足:集合空间 R n R^n Rn的度量性质(如长度、夹角)等没有涉及。
因此引入欧式空间,在欧式空间中定义內积,用內积反映向量的长度、夹角等度量性质:
长度: ∣ α ∣ = α ⋅ α |α|=\sqrt{α\cdotα} ∣α∣=α⋅α
夹角 < α , β > <α,β> <α,β>: c o s < α , β > = α ⋅ β ∣ α ∣ ∣ β ∣ cos<α,β>=\frac{α\cdotβ}{|α||β|} cos<α,β>=∣α∣∣β∣α⋅β
.
总的来说,欧式空间 V V V是特殊的线性空间
(1) V V V是实数域 R R R上的线性空间;
(2) V V V除向量的线性运算外,还有“內积”运算;
(3) ( α , β ) ∈ R (α,β)\in R (α,β)∈R。
.
欧式空间=线性空间+內积运算
参考文献:
[1] 欧式空间的定义与基本性质_课件
[2] 用距离解释向量空间、內积空间、欧式空间以及希尔伯特空间的关系 -
希尔伯特空间
在内积空间上扩展,使得内积空间满足完备性,形成希尔伯特空间如下:
欧式空间+完备性=希尔伯特空间
完备性的意思就是空间中的极限运算不能跑出该空间。
如有理数空间中的2–√2的小数表示,其极限随着小数位数的增加收敛到2–√2,但2–√2属于无理数,并不在有理数空间,故不满足完备性。
一个通俗的理解是把学校理解为一个空间,你从学校内的宿舍中开始一直往外走,当走不动停下来时(极限收敛),发现已经走出学校了(超出空间),不在学校范围内了(不完备了)。希尔伯特就相当于地球,无论你怎么走,都还在地球内(飞出太空除外)。
参考网址:用距离解释向量空间、內积空间、欧式空间以及希尔伯特空间的关系
3 硬间隔支持向量机与硬间隔最大化
3.1 硬间隔支持向量机
笔者概述:
三个支持向量机模型都是将输入空间中的输入映射为特征空间中的特征向量,所以输入都由输入空间映射到特征空间,支持向量机的学习是在特征空间进行的。
书籍原文:


笔者概述:
注意给定的训练数据集是特征空间上的,即映射后的。
分离超平面: w x + b = 0 w^x+b=0 wx+b=0。由法向量 w w w和截距 b b b决定,法向量指向的一侧为正类。
硬件支持向量机训练完成后,包括两部分:
1)分离超平面: w ∗ x + b = 0 w^*x+b=0 w∗x+b=0。
2)分类决策函数: s i g n ( w ∗ x + b ) sign(w^*x+b) sign(w∗x+b)。这是一个符号函数,可参考sign函数_百度百科。
3.2 函数间隔和几何间隔
3.2.1 函数间隔
笔者概述:
函数间隔:这个概念不是数学中挪用过来的,而是本就在支持向量机中提出的。
因为如下两点,所以可用量 y ( w ⋅ x + b ) y(w\cdot x+b) y(w⋅x+b)表示分类的正确性及确信度。
- 确信度:一个点距离超平面的远近可以表示分类预测的确信程度, ∣ w ⋅ x + b ∣ |w\cdot x+b| ∣w⋅x+b∣可以表示点 x x x距离超平面的远近。
- 正确性: w ⋅ x + b w\cdot x+b w⋅x+b的符号与类标记的符号 y y y是否一致能够表示分类是否正确。
函数间隔定义:
超平面 ( w , b ) (w,b) (w,b)关于样本点 ( x i , y i ) (x_i,y_i) (xi,yi)的函数间隔为 γ i ‾ = y i ( w ⋅ x i + b ) \overline{\gamma_i} = y_i(w \cdot x_i + b) γi=yi(w⋅xi+b)。
超平面 ( w , b ) (w,b) (w,b)关于训练数据集T的函数间隔为超平面 ( w , b ) (w,b) (w,b)关于 T T T中所有样本点 ( x i , y i ) (x_i,y_i) (xi,yi)的函数间隔之最小值,即 min γ i ‾ \min\overline{\gamma_i} minγi。
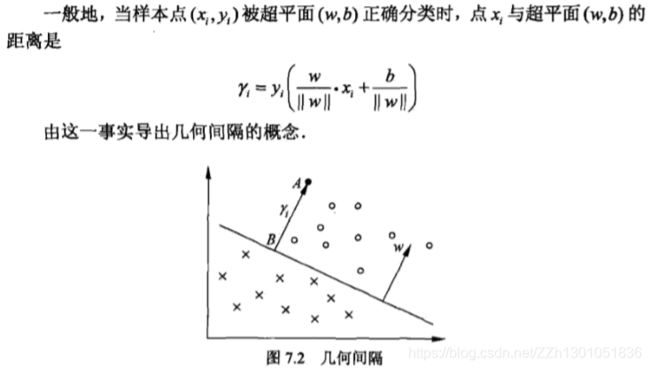
3.2.2 几何间隔
几何间隔的提出
笔者概述:
- 函数间隔的缺点:只要成比例地改变 w w w和 b b b,,例如将其改为 2 w 2w 2w和 2 b 2b 2b,超平面不会变,但是函数间隔却会成为原来的两倍。
- 解决方法:给分离超平面的法向量 w w w加约束, 使得间隔是确定的。可加约束例如,要求法向量是单位法向量,即模为1( ∣ ∣ w ∣ ∣ = 1 ||w||=1 ∣∣w∣∣=1)。那么分离超平面的公式就变为 w ∣ ∣ w ∣ ∣ x + b ∣ ∣ w ∣ ∣ = 0 \frac{w}{||w||}x+\frac{b}{||w||}=0 ∣∣w∣∣wx+∣∣w∣∣b=0,将分离超平面公式两端同除以法向量的模||w||。
这时函数间隔成为几何间隔,公式为 y i ( w ∣ ∣ w ∣ ∣ x + b ∣ ∣ w ∣ ∣ ) y_i(\frac{w}{||w||}x+\frac{b}{||w||}) yi(∣∣w∣∣wx+∣∣w∣∣b)