利用手机进行声源运动追踪的相关论文
关键词:acoustic motion tracking
曲线的凸性
曲线的凹或凸统称为曲线的凸性。
- 从切线角度讲,下凸弧上过任一点的切线都在曲线弧之下,而上凸弧上过任一点的切线都在曲线弧之上。
- 从割线角度讲,如果连续曲线y=f(x)在区间(a,b)对应的曲线弧上任意两点的割线线段都在该两点间的曲线弧之上,则称该段曲线弧是下凸的,并称函数y=f(x)在区间(a,b)上是下凸的(或上凹的,即曲线开口向上)。如果连续曲线y=f(x)在区间(a,b)对应的曲线弧上任意两点的割线线段都在该两点间的曲线弧之下,则称该段曲线弧是上凸的,并称函数y=f(x)在区间(a,b)上是上凸的(或下凹的,即曲线开口向下)。
- 从导数角度讲,设y=f(x)在(a,b)内具有二阶导数,如果在(a,b)内 f ′ ′ ( x ) > 0 f''(x)>0 f′′(x)>0,则y=f(x)在(a,b)内为下凸;如果在(a,b)内 f ′ ′ ( x ) < 0 f''(x)<0 f′′(x)<0,则y=f(x)在(a,b)内为上凸。
意义
在研究函数图形的变化时,仅仅研究单调性并不能完全反映它的变化规律。如下图,函数虽然在区间[a,b]内单调递增,但却有不同的弯曲状况,从左到右,曲线先是向下凹,通过P点后改变了弯曲方向,曲线向上凸。因此,在研究函数的图形时,除了研究其单调性,对于它的弯曲方向及弯曲方向的改变点的研究也是很有必要的。从图1明显可知,曲线向下凹时,弯曲的弧段位于这弧段上任意一点的切线的上方,曲线向上凸时,弯曲的弧段位于这弧段上任意一点的切线的下方。

1、CAT
参考论文:CAT: High-Precision Acoustic Motion Tracking
传统的FMCW方法

每个周期内,一个chirp信号线性地从 f m i n f_{min} fmin增加到 f m a x f_{max} fmax,因此频率表示为: f = f m i n + B T t f=f_{min}+\frac BTt f=fmin+TBt,其中B是带宽,T为chirp的周期。
对频率进行积分得到想要相位: u ( t ) = 2 π ( f m i n t + B t 2 2 T ) u(t)=2\pi(f_{min}t+B\frac{t^2}{2T}) u(t)=2π(fmint+B2Tt2)
因此,在第n个周期的传输信号为: v t ( t ′ ) = c o s ( 2 π f m i n t ′ + π B t ′ 2 T ) v_t(t')=cos(2\pi f_{min}t'+\frac{\pi Bt'^2}T) vt(t′)=cos(2πfmint′+TπBt′2),其中 t ′ = t − n T t'=t-nT t′=t−nT
线性调频信号在延迟 t d t_d td之后传输到达接收方,接收到的信号被衰减并延迟时间,变为:
v r = α c o s ( 2 π f m i n ( t ′ − t d ) + π B ( t ′ − t d ) 2 T ) v_r=\alpha cos(2\pi f_{min}(t'-t_d)+\frac{\pi B(t'-t_d)^2}T) vr=αcos(2πfmin(t′−td)+TπB(t′−td)2)
其中, α \alpha α为信号衰减
接收方将收到的信号和发送的信号混合, v m ( t ) = v r ( t ) v t ( t ) v_m(t)=v_r(t)v_t(t) vm(t)=vr(t)vt(t)
因为 c o s A c o s B = ( c o s ( A − B ) + c o s ( A + B ) ) / 2 cosAcosB=(cos(A-B)+cos(A+B))/2 cosAcosB=(cos(A−B)+cos(A+B))/2,并过滤掉高频部分cos(A + B),得:
v m ( t ) = α c o s ( 2 π f m i n t d + π B ( 2 t ′ t d − t d 2 ) T ) v_m(t)=\alpha cos(2\pi f_{min}t_d+\frac{\pi B(2t't_d-t_d^2)}T) vm(t)=αcos(2πfmintd+TπB(2t′td−td2))
假设发送方与接收方相距R,发送方以v的速度移动, t d = R + v t ′ c t_d=\frac{R+vt'}c td=cR+vt′,带入上式得:
α c o s ( 2 π f m i n R + v t ′ c + 2 π B t ′ ( R + v t ′ ) c T − π B ( R + v t ′ ) 2 c 2 T ) \alpha cos(2\pi f_{min}\frac{R+vt'}c+\frac{2\pi Bt'(R+vt')}{cT}-\frac{\pi B(R+vt')^2}{c^2T}) αcos(2πfmincR+vt′+cT2πBt′(R+vt′)−c2TπB(R+vt′)2)
通过取相位的导数来分析上式得频率部分,其中,常数项可以忽略,关于 1 c 2 {\frac1c}^{2} c12的二次项太小也可以忽略,并且t’的平均值为T/2,得到:
f p = 1 2 π δ P h a s e δ t ′ = B R c T + f m i n v c + B v c f_p=\frac1{2\pi}\frac{\delta Phase}{\delta t'}=\frac{BR}{cT}+\frac{f_{min}v}c+\frac{Bv}c fp=2π1δt′δPhase=cTBR+cfminv+cBv
当v接近于0时,频谱的第一个峰值为 B R c T \frac{BR}{cT} cTBR
如果发送方和接收方之间存在多路径传播,在混合信号的频谱中观察到多个峰值,在这种情况下 f p f_p fp由第一个峰值决定,该峰值对应于直接路径。通过测量第一个峰值 f p f_p fp,距离 R = f p c T B R =\frac {f_pcT}{B} R=BfpcT
论文中使用的分布式FMCW方法
Step1:在接收信号上进行一次近似同步

如上图所示,近似同步保证每个处理周期都与单个chirp对齐,每次处理一个完整的chirp。
具体方法是将接收到的信号与原始chirp信号互相关(correlation),选择检测到最高相关峰的时间作为第一个处理周期的开始时间,同步只需要在开始时执行一次。

如上图,由于互相关通常会显示多个幅度相似的峰,因此同步是近似的。
Step2:引入pseudo-transmission time
由于在每个处理周期中,要将接收信号与发送信号混合,但是我们不知道发送信号开始的具体时间,因此,引入了pseudo-transmission time(接收方假设传输信号开始的时间,下图绿色虚线所示)

t0为第一个chirp中pseudo transmission time和实际发送时间之差,并且对于接收方来说是一个未知的常数,因此,在每个处理周期,估计距离相对于实际距离偏移一个常数:
R n = c T f n p B + c t 0 R_n=\frac{cTf_n^p}B+ct_0 Rn=BcTfnp+ct0
其中, R n R_n Rn为在第n个处理周期中发送方和接收方的距离, f n p f^p_n fnp是第n个处理周期中混合信号的峰值,c是声信号的传播速度,T是chirp的周期,B是信号带宽( B = f m a x − f m i n B=f_{max}-f_{min} B=fmax−fmin)。
根据上述等式,接着考虑两个处理周期:
R n − R 1 = ( f n p − f 1 p ) c T B R_n-R_1=(f_n^p-f_1^p)\frac{cT}B Rn−R1=(fnp−f1p)BcT
由于这个常数偏移,我们仅可以测量距离的变化量。要随时获取绝对距离,我们需要知道某个点(称为参考点)的绝对距离,并使用距离变化来获取新位置的绝对距离,即:
R n = ( f n p − f 1 p ) c T B + R 1 R_n=(f_n^p-f_1^p)\frac{cT}B+R_1 Rn=(fnp−f1p)BcT+R1
其中, R 1 R_1 R1就是参考点相对于扬声器的绝对距离
Step3:估计参考点
为了获得距离 R n R_n Rn,我们需要知道手机在某个点(称之为参考点)上与扬声器之间的绝对距离。
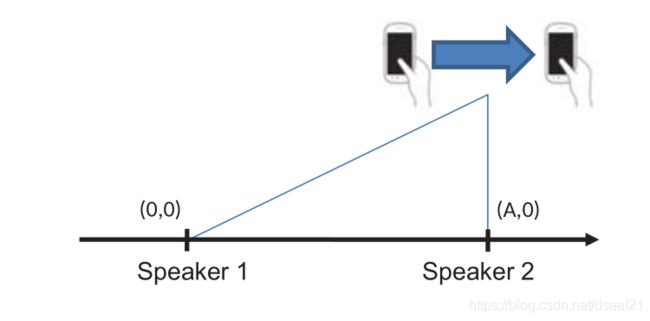
假设两个speaker分别位于(0,0)和(A,0)的位置,让移动设备沿x轴(两个扬声器之间的连线)来回移动。
当移动设备移动向speaker2时,它在接近speaker2并且在x=A之前,经历正多普勒频移;当经过x=A后,并且远离speaker2时,经历负多普勒频移。因此,我们可以检测到多普勒频移改变其符号的时间,并且那时移动设备移动到x = A上的一个点,就是我们的参考点。
假设参考点距离两个speaker的距离分别为D1和D2,我们可以通过让两个speaker相同时间开始发送信号并且使用相同的pseudo-transmission time(此时t0是相同的),然后使用FMCW测距D1与D2之差 Δ D \Delta D ΔD:
Δ D = D 1 − D 2 = c T ( f p , 1 − f p , 2 ) B \Delta D=D1-D2=\frac{cT(f_{p,1}-f_{p,2})}B ΔD=D1−D2=BcT(fp,1−fp,2)
又因为勾股定理: D 1 2 − D 2 2 = A 2 D1^2-D2^2=A^2 D12−D22=A2,我们可以得到D1和D2的值
Step4:考虑接收方运动的影响
为了简便,上述公式忽略了接收方运动的影响,但是不可忽略的速度会导致混合信号的峰值频率的额外频移。
因为 f p = B R c T + f m i n v c + B v c f_p = \frac{BR}{cT} + \frac{f_{min}v}{c}+ \frac{Bv}{c} fp=cTBR+cfminv+cBv,并且由于pseudo-transmission时间 t 0 t_0 t0,这个周期中的测量值与实际值 R n R_n Rn相差 c t 0 ct_0 ct0,因此得到下式:
- f n p = B ( R n − c t 0 ) c T + f m i n v n c + B v n c f_n^p=\frac{B(R_n-ct_0)}{cT}+\frac{f_{min}v_n}c+\frac{Bv_n}c fnp=cTB(Rn−ct0)+cfminvn+cBvn
其中, v n v_n vn是接收方相对于发送方在第n个处理周期的速度,为了简单,假设在第一个处理周期中是静止的(可以作为参考点)
- R n = ( f n p − f m i n v n c − B v n c − f 1 p ) c T B + R 1 R_n=(f_n^p-\frac{f_{min}v_n}c-\frac{Bv_n}c-f_1^p)\frac{cT}B+R_1 Rn=(fnp−cfminvn−cBvn−f1p)BcT+R1
根据上式,绝对距离 R n R_n Rn由第1个和第n个处理周期的峰值频率 f n p 、 f 1 p f_n^p、f_1^p fnp、f1p,基于多普勒频移的第n个处理周期接收方的速度 v n v_n vn,和参考点的距离 R 1 R_1 R1决定
这里对速度的测量是利用多普勒频移
当接收方运动而发送方静止时, v = F s F c v=\frac{F^s}Fc v=FFsc,其中F是信号的原始频率, F s F^s Fs为多普勒频移,c为声音的传播速度
利用如下步骤测量移动速度v:
①每个扬声器发送听不见的频率上的正弦波,不同的扬声器使用不同的频率
②接收方以44.1 KHz(标准采样率)对接收到的音频信号进行采样,应用Hanning窗以避免频率泄漏,然后使用短时傅立叶变换(STFT)提取频率。 我们使用1764个样本来计算STFT,这相当于40毫秒内的音频样本。然后,我们得到峰值频率,并将其减去原始正弦波的频率得到 F s F_s Fs
③为了提高准确度,我们让每个扬声器在不同的频率上发射多个正弦波,让接收方估计每个频率上的频移,并通过去除异常值和平均剩余的值得到最后的 F s F_s Fs。
Step5:考虑频率偏移
由于不完美的时钟,发送方和接收方的采样率不完全相同,也就是说发送方和接收方采样相同的点数花费不同的时间,因此也就引入的误差。
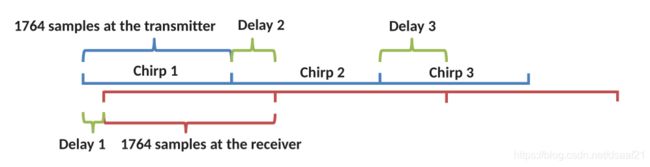
如上图,发送方传输一个由1764个采样点构成的chirp,在经历了Delay1的时间后,该chirp被接收方收到。由于接收器的时钟速率略有不同,因此接收器累积这1764个采样所需的时间稍长一些,所以Delay2不仅包括传输延迟还包括不同时钟速率造成的采样时间差。Delay3同理。
如果发送方和接收方是静态的,并且它们的采样率偏移是恒定的,则估计的延迟将随时间线性增加。为了补偿这种影响,我们在开始时引入了一个简短的校准阶段,我们会在校准过程中固定接收器的位置。
如果没有采样频率偏移,则FMCW检测到的峰值频率应固定,采样频率偏移将导致峰值频率随时间稳定变化,我们可以通过绘制随时间变化的峰值频率来估计偏移(对测量数据应用最小二乘拟合):
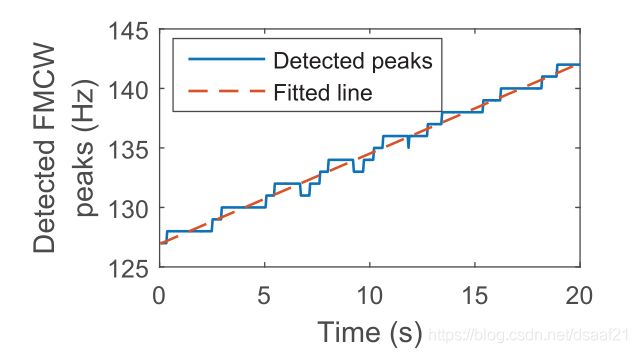
图中红虚线的斜率为k,我们按以下方式处理原始测量:
f p a d j u s t e d = f p r a w − k t f_p^{adjusted}=f_p^{raw}-kt fpadjusted=fpraw−kt
其中 f p a d j u s t e d f^{adjusted}_p fpadjusted和 f p r a w f_p^{raw} fpraw分别表示调整后的和原始的峰值频率,t是校准阶段经过的时间,k是拟合线的斜率
采样频率偏移可能会随时间缓慢变化,当接收器静止时,重新校准频率偏移。
Step6:优化框架,得到最合适的移动方坐标
结合了多普勒频移和FMCW测量,可进行精确的运动跟踪的优化框架:
∑ i ∈ [ k − n + 1.. k ] ∑ j α ( ∣ z i − c j ∣ − ∣ z 0 − c j ∣ − d F M C W i , j ) 2 + ∑ i ∈ [ k − n + 2.. k ] ∑ j β ( ∣ z i − c j ∣ − ∣ z i − 1 − c j ∣ − v i − 1 , j d o p p l e r T ) 2 \sum_{i\in [k-n+1..k]}\sum_j\alpha(|z_i-c_j|-|z_0-c_j|-d_{FMCW}^{i,j})^2+\\ \sum_{i\in [k-n+2..k]}\sum_j\beta(|z_i-c_j|-|z_{i-1}-c_j|-v_{i-1,j}^{doppler}T)^2 i∈[k−n+1..k]∑j∑α(∣zi−cj∣−∣z0−cj∣−dFMCWi,j)2+i∈[k−n+2..k]∑j∑β(∣zi−cj∣−∣zi−1−cj∣−vi−1,jdopplerT)2
其中,k是当前的处理周期,n是用于该优化的周期数, z i z_i zi表示在i个周期开始的时候移动方的位置, z 0 z_0 z0表示参考点的位置, c j c_j cj表示第j个周期扬声器的位置, d F M C W i , j d_{FMCW}^{i,j} dFMCWi,j表示在第i个周期中相对于第j个扬声器的参考点距离变化, v i , j d o p p l e r v_{i,j}^{doppler} vi,jdoppler表示在第i个周期中相对于第j个扬声器的速度。
优化框架反映了找到最适合FMCW和Doppler方法的移动方坐标,利用了多个周期来提高准确率。
第一项捕获基于坐标计算的距离应与从FMCW估计的距离相匹配,第二项捕获在从坐标计算的间隔内的行进距离应与从多普勒频移得出的距离相匹配。
上述的优化问题是非凸的,意味着不保证收敛并且计算开销大。上述公式中未知项为移动方的坐标,为了简化该问题,将移动方相对于扬声器的距离作为未知项,即将上述公式中的 ∣ z i − c j ∣ |z_i-c_j| ∣zi−cj∣替换成 D i , j D_{i,j} Di,j。
实现
搭建了两个平台:第一个平台由带扬声器的电脑和一台安卓手机组成,第二个平台由外置麦克风(发送声音信号)和移动手机(分析接收到的声音信号来实时追踪它的位置)。
多普勒频移测速:使用正弦波;频率带宽为1 KHz,其中包括五个以200 Hz分开的五个不同频率的正弦波,以避免相互干扰 。
FMCW测距:使用锯齿波,每个chirp信号带宽为2.5kHz。
正弦信号和chirp信号叠加一起发送,收到后使用滤波来区分?一个周期为40ms?
这些信号由Matlab生成并保存在标准的wav音频文件中,可以直接从通用扬声器播放
两个扬声器的2D tracking: 使用两个扬声器,为多普勒频移测量分配1kHz的带宽,为FMCW测量分配2.5kHz的带宽,并且让两个扬声器交替发送线性调频序列以共享该频带(时分复用)。一个扬声器发送从17 KHz到19.5KHz的chirp,而另一个扬声器发送从19.5 KHz到17 KHz的chirp, 这有助于区分来自不同扬声器的信号。在用于多普勒频移测量和FMCW估计的频率之间有一个500 Hz的保护带宽。因此音频信号占据了14.5kHz到19.5kHz。
三个扬声器的2D tracking: 每个扬声器占据4KHz的频带,其中1KHz分配给多普勒测量,2.5KHz分配给FMCW测量,0.5KHz是保护带宽。因此音频信号占据了6.5KHz到19.5KHz。
四个扬声器的3D tracking: 前两个扬声器通过交替发送线性调频信号,共享用于FMCW测量的2.5 KHz频带,即时分复用;同理,后两个扬声器也如此。并且每个扬声器分配1KHz频带给多普勒频移测量。因此音频信号占据了9.5KHz到19.5KHz。
当使用三个及以上的扬声器时,有一部分音频信号就是可以听见的了,为了让它们不可听见,一种选择是让它们交替发送线性调频序列和正弦波,即同时利用时分复用和频分复用。
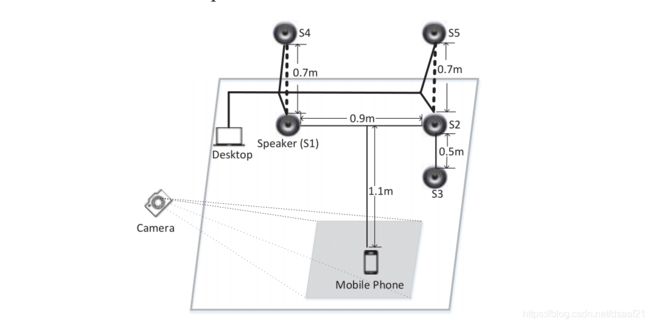
两个扬声器的系统中,扬声器的默认间隔为90cm;三个扬声器的系统中,第3个扬声器S3如上图摆放,距S2的距离为0.5m;四个扬声器的系统中,如S1、S2、S4、S5那样摆放。
2、AAmouse
参考论文:Turning a Mobile Device into a Mouse in the Air
步骤
测量多普勒频移
使用44.1KHz的采样率进行采样,这意味着使用44100个采样点(花费1s)进行FFT来分析信号的频域,但是一次长的FFT并不能允许我们实时追踪设备。
为了解决这个问题,我们采用短时傅里叶变换(STFT)来分析频率随时间的变化,它比FFT需要更少的采样点,输入的缺失值用0补充。并且,为了减小失真,在时域中采用了加窗技术,每个窗口包含当前STFT处理间隔中的所有音频样本,为此我们使用汉明窗。
在该设计中,输入的长度设置为44100,使用1764个音频样本(即40毫秒内的音频样本总数)并在其后补0将输入长度补充道44100作为输入,这使FFT的输出每40毫秒具有1 Hz的分辨率。 从中,我们通过找到峰值频率(即具有最高值的频率)并减去原始信号频率来测量多普勒频移。
短时傅里叶变换(STFT): 它用以确定时变信号其局部区域正弦波的频率与相位。其思想是:选择一个时频局部化的窗函数,假定分析窗函数g(t)在一个短时间间隔内是平稳(伪平稳)的,移动窗函数,使f(t)g(t)在不同的有限时间宽度内是平稳信号,从而计算出各个不同时刻的频谱。 简单来说,短时傅里叶变换就是先把一个函数和窗函数进行相乘,然后再进行一维的傅里叶变换。并通过窗函数的滑动得到一系列的频谱函数,将这些结果依次展开便得到一个二维的时频图。 即,短时傅里叶变换能得到频率随时间的变化图。
第二种解释:采用滑动窗口机制,设定窗口(窗函数,例如汉宁窗)大小和步长,让窗口在时域信号上滑动,分别计算每个窗口的傅立叶变换,形成了不同时间窗口对应的频域信号,拼接起来就成为了频率随时间变化的数据(时频信号)。

基于多普勒频移估计速度
测量得到多普勒频移后,当发送端静止而接收端相对运动时,利用下列公式测得接收端的速度:
v = F s F C v=\frac{F^s}FC v=FFsC
其中F是信号的原始频率; F s F^s Fs是接收信号频率与发送信号频率之差,即多普勒频移;c是声波的传播速度;v是接收源相对发送源的移动速度。
追踪移动设备(接收方)的位置
首先,假设扬声器之间的距离和移动设备的初始位置已知。
D表示扬声器之间的距离,X轴与两个扬声器之间的连线平行,左扬声器为坐标原点,由此构造一个虚拟的二维坐标平面。那么,左扬声器坐标为(0,0),右扬声器坐标为(D,0)。
令,移动设备的初始位置为 ( x 0 , y 0 ) (x_0,y_0) (x0,y0),移动设备到扬声器1和扬声器2的距离分别为 D 0 , 1 和 D 0 , 2 D_{0,1}和D_{0,2} D0,1和D0,2, t S t_S tS为测量多普勒频移时的采样间隔(该设计中使用的是40ms,意味着移动设备的位置每40ms更新一次)。
在经过时间 t s t_s ts后,通过多普勒频移得到移动设备距离两个扬声器的新距离 D 1 , 1 , D 1 , 2 D_{1,1},D_{1,2} D1,1,D1,2:
D 1 , 1 = D 0 , 1 + ( F 1 , 1 s F 1 c ) t s D_{1,1}=D_{0,1}+(\frac{F_{1,1}^s}{F_1}c)t_s D1,1=D0,1+(F1F1,1sc)ts
D 1 , 2 = D 0 , 2 + ( F 1 , 2 s F 2 c ) t s D_{1,2}=D_{0,2}+(\frac{F_{1,2}^s}{F_2}c)t_s D1,2=D0,2+(F2F1,2sc)ts
其中, F k 和 F i , k s F_k和F_{i,k}^s Fk和Fi,ks分别是声音的频率和在第i个采样间隔内从扬声器k发生的多普勒频移。

得到与扬声器之间的更新距离后,接下来就是得到新的位置,新位置是圆心分别为(0,0)、(D,0),半径分别为 D 1 , 1 , D 1 , 2 D_{1,1},D_{1,2} D1,1,D1,2的两个圆的交点。我们可以利用如下公式高效地得到两个圆的交点:
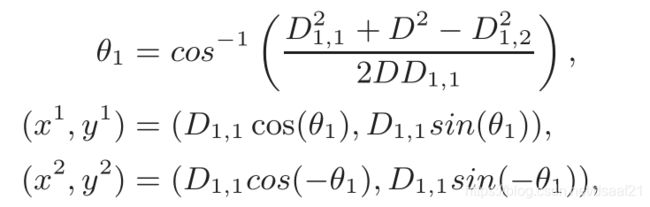
其中, ( x 1 , y 1 ) , ( x 2 , y 2 ) (x^1,y^1),(x^2,y^2) (x1,y1),(x2,y2)分别是圆的两个交点。
如果 D 1 , 1 + D 1 , 2 < D D_{1,1}+D_{1,2}
提高准确度
让每个扬声器在不同的频率上发射多个正弦波,使用它们来测量多普勒频移(5个不同的频率能将准确率提高26%)。在运动中,如果不同的频率相隔太近,它们会相互干扰,因此为了保守起见,相邻的频率间隔200Hz。
这里使用最大比合并Maximal Ratio Combining (MRC) 技术提高准确度,该技术是通过噪声方差的倒数加权平均接收信号。在使用MRC之前,需要首先移除异常值。在两个相邻的采样间隔中,如果频移( ∣ F i + 1 , k s − F i , k s ∣ |F_{i+1,k}^s-F_{i,k}^s| ∣Fi+1,ks−Fi,ks∣)大于10Hz,那么我们就认为这是一个异常值,并把他移除。在MRC之后,应用卡尔曼滤波来平滑估计的多普勒频移,我们将卡尔曼滤波器中的过程噪声协方差Q和测量噪声协方差R均设置为0.00001。
测量两个扬声器之间的距离
该实验我复现过,误差特别大,麻烦各位大神指定
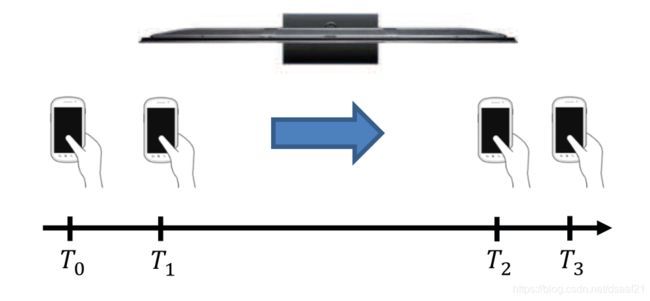
如上图所示,扬声器发出听不见的声波并且移动设备使用麦克风进行记录。手握移动设备从左扬声器向右扬声器直线移动,移动到右端停止然后返回左端,可以重复此过程几次提高准确度(实验表明,3次重复是足够的)。
根据多普勒效应,当接收方靠近发送方时,多普勒频移为正;当接收方远离发送方时,多普勒频移为负。因此,我们可以轻松地检测到设备经过左右扬声器的时间,并通过基于多普勒频移计算运动速度来测量距离。
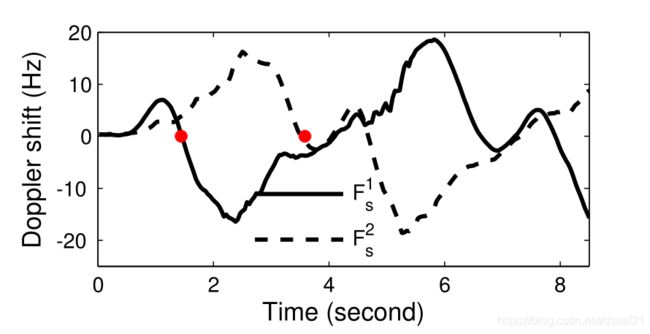
如上图,当设备在两个扬声器的左边时, F s 1 和 F s 2 F_s^1和F_s^2 Fs1和Fs2均为正,当1.48s通过左扬声器后, F s 1 F_s^1 Fs1变为负而 F s 2 F_s^2 Fs2保持为正。同理,当通过右扬声器后, F s 1 F_s^1 Fs1保持为负而 F s 2 F_s^2 Fs2变为负。通过找到这些点,我们可以找到用户在两个扬声器之间移动所花费的时间,并使用多普勒频移测量距离。
为了提高精度,我们在每个方向(来和去两个方向)上获得一个距离估计值,并在两个方向上平均估计的距离。
寻找移动设备的初始位置
使用粒子滤波particle filter。首先,我们生成均匀分布地许多粒子,每个粒子表示移动设备可能的初始位置。然后,在下一个多普勒采样间隔中,它将确定当前粒子的运动, 如果移动不可行,则将粒子过滤掉(当 D 1 , 1 + D 1 , 2 < D D_{1,1}+D_{1,2}
让P表示粒子的集合, P = { ( x 0 1 , y 0 1 ) , . . . , ( x 0 N , y 0 N ) } P=\{(x_0^1,y_0^1),...,(x_0^N,y_0^N)\} P={(x01,y01),...,(x0N,y0N)},其中 ( x 0 k , y 0 k ) (x_0^k,y_0^k) (x0k,y0k)表示第k个粒子的初始位置,N表示粒子的个数。在新的多普勒采样间隔期间,不可行的粒子运动将从P中滤除 ,在第i次运动后,第(i+1)次采样的位置由平均利用第i次粒子位置和第(i+1)次粒子位置的差别追踪,那就是:

其中, ∣ P ∣ |P| ∣P∣是P中剩余粒子的个数。
我们使用625个粒子在准确性和复杂度之间进行平衡。
实验评估了初始位置误差对跟踪精度的影响,它表明跟踪精度对初始位置误差不敏感 。请注意,实验中确定初始位置不是因为想知道设备的确切初始位置,而是因为我们需要它来跟踪下一个位置。 无论设备的物理位置如何,光标始终从屏幕中心开始,因此,初始位置误差不会直接转化为跟踪误差。
实现
因为追踪的计算量不可忽略,所有的处理都交给处理单元,移动设备只负责传输记录的音频数据给处理器(通过Android debug bridge)。在实时处理中,主要的处理开销是FFT。
在一次多普勒采样周期(40ms)中:
1)进行一次44100个点的FFT(40ms只有1764个采样点,缺失的值补0)
2)每个频带进行了FFT后寻找峰值频率
3)去除了异常值后将它们合并
4)计算每个粒子的位置
使用两个扬声器,扬声器之间的距离为0.9m,移动设备距离扬声器大约2m,左右两个扬声器分别使用17kHz-19kHz和19kHz-21kHz的音频,每个扬声器发出10中不同频率的声音,每种频率相隔200Hz。
3、MilliSonic
参考论文:MilliSonic: Pushing the Limits of Acoustic Motion Tracking
使用FMCW信号的相位来计算距离,包括如下两步:
1)在时域应用动态窄带带通滤波器来滤除大部分与直接路径相距较远的多径,这使得我们只剩下了直接路径周围剩余的一小部分间接路径。
2)从瞬时FMCW相位提取距离信息。
论文中提到的传统FMCW方法
FMCW信号的数学表达:
x ( t ) = e x p ( − j 2 π ( f 0 + B 2 T t ) t ) = e x p ( − j 2 π ( f 0 t + B 2 T t 2 ) ) x(t)=exp(-j2\pi(f_0+\frac B{2T}t)t)=exp(-j2\pi(f_0t+\frac B{2T}t^2)) x(t)=exp(−j2π(f0+2TBt)t)=exp(−j2π(f0t+2TBt2))
其中, f 0 , B , T f_0,B,T f0,B,T分别表示初始频率,带宽,FMCW chirp的周期。
因为多径,收到的信号表达为:
y ( t ) = ∑ i = 1 M A i e x p ( − j 2 π ( f 0 ( t − t i ) + B 2 T ( t 2 + t i 2 − 2 t t i ) ) ) y(t)=\sum_{i=1}^MA_iexp(-j2\pi(f_0(t-t_i)+\frac B{2T}(t^2+t_i^2-2tt_i))) y(t)=i=1∑MAiexp(−j2π(f0(t−ti)+2TB(t2+ti2−2tti)))
其中, A i A_i Ai表示为振幅, t i = d i ( t ) c t_i=\frac{d_i(t)}c ti=cdi(t)是第i条路径的达到时间
y(t)除以x(t)得等式(1):
y ^ ( t ) = ∑ i = 1 M A i e x p ( − j 2 π ( B T t i t + f 0 t i − B 2 T t i 2 ) ) , ( 1 ) \hat y(t)=\sum_{i=1}^MA_iexp(-j2\pi(\frac BTt_it+f_0t_i-\frac B{2T}t_i^2)),(1) y^(t)=i=1∑MAiexp(−j2π(TBtit+f0ti−2TBti2)),(1)
上式表明了不同到达时间的多径落入不同的频率,那么通过使用DFT得到第一个峰值频率 f p e a k f_{peak} fpeak,对应于相对于发送方的直接路径。因此可以计算得到该直接路径 d ( t ) = c f p e a k B d(t)=\frac{cf_{peak}}B d(t)=Bcfpeak
使用相位测距的算法步骤
①利用自适应的带通滤波器消除离直接路径较远的多径
对于第一个FMCW chirp,使用DFT在频域中提取解调信号(混合信号)的第一个峰值,类似于等式(1) 的设计。然后使用FIR滤波器,仅在峰值附近留下窄范围的频带。根据声音信号的SNR自适应地设置FIR滤波器的时延:当SNR>10dB,使用15ms的时延;否则,使用30md的时延。
对于随后的FMCW chirps,不再使用DFT提取峰值频率。相反,对于第 i + 1 i+1 i+1个FMCW线性调频脉冲,我们从第 i i i个线性调频脉冲末尾估计的距离和速度推断出新的峰值,然后再在新峰值的附近使用FIR滤波器。
根据第 i i i个线性调频脉冲末尾估计的距离和速度,我们能够推出当前线性调频脉冲开始的距离:
d ^ s t a r t ( i + 1 ) = d e n d ( i ) + v e n d ( i ) δ T , 其 中 δ T 是 两 个 c h i r p 之 间 的 间 隔 ( 解 释 如 下 ) \hat d_{start}^{(i+1)}=d_{end}^{(i)}+v_{end}^{(i)}\delta T,其中\delta T是两个chirp之间的间隔(解释如下) d^start(i+1)=dend(i)+vend(i)δT,其中δT是两个chirp之间的间隔(解释如下)
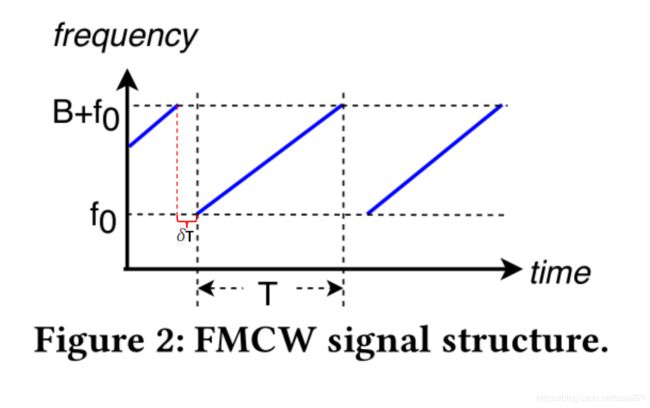
如上图,因为两个chirp之间不是连续发送的,因此 δ T \delta T δT如上图标示,当两个chirp之间连续发送时, δ T = 0 , d ^ s t a r t ( i + 1 ) = d e n d ( i ) \delta T=0,\hat d_{start}^{(i+1)}=d_{end}^{(i)} δT=0,d^start(i+1)=dend(i)
上述这么做基于两个理由:①该距离估计方法比DFT峰值估计的结果更准确②与在整个FMCWchirp上执行的DFT不同,我们不需要在处理之前接收完整的FMCW chirp
得到 d ^ s t a r t ( i + 1 ) \hat d_{start}^{(i+1)} d^start(i+1)后,利用 d ( t ) = c f p e a k B d(t)=\frac{cf_{peak}}B d(t)=Bcfpeak求得新峰值,然后再在新峰值的附近使用FIR滤波器,供第②步从相位中提取出距离。
最后,因为多普勒效应会模糊频域中的峰值,前一个chirp结束时的速度超过给定阈值时,自适应地增加通带宽度。在我们的算法中,当速度不超过1m/s时,我们将通带宽度设置为1Hz;否则,我们将通带宽度设置为2Hz。
②从FMCW相位中提取出距离(相当于求第 i i i个线性调频脉冲末尾估计的距离 d e n d ( i ) d_{end}^{(i)} dend(i))
上述处理过程消除了所有到达时间比直接路径长得多的多径的影响,只剩下了直接路径周围剩余的一小部分间接路径。因此,当没有阻碍时,剩余间接路径的总幅值要比直接路径的小,可以忽略。
根据等式(1),估计的相位为( t t t位于 0 ∽ T 0\backsim T 0∽T之间):
ϕ ( t ) ≈ − 2 π ( B T t t d + f 0 t d − B 2 T t d 2 ) , 其 中 t d 是 直 接 路 径 的 到 达 时 间 \phi(t)\approx-2\pi(\frac BTtt_d+f_0t_d-\frac B{2T}t_d^2),其中t_d是直接路径的到达时间 ϕ(t)≈−2π(TBttd+f0td−2TBtd2),其中td是直接路径的到达时间
该估计假设我们已经应用了动态过滤器来滤除大多数到达路径距离比直接路径距离大得多的多径
上述关于 t d ( t , ϕ ( t ) ) t_d(t,\phi(t)) td(t,ϕ(t))的二次方程可以唯一求解,但是该方程式的两个解中只有一个在FMCW chirp的范围[0,T]内**(FMCW的周期T要设置成发送的信号能在T之内到达接收方)**。距离 d ( t , ϕ ( t ) ) d(t,\phi(t)) d(t,ϕ(t))可以利用 c t d ( t , ϕ ( t ) ) ct_d(t,\phi(t)) ctd(t,ϕ(t))求得。
该方法估计的距离误差上限为: s i n − 1 ( A 2 / A 1 ) c 2 π ( f 0 − B / 2 ) \frac{sin^{-1}(A_2/A_1)c}{2\pi(f_0-B/2)} 2π(f0−B/2)sin−1(A2/A1)c,其中 s i n − 1 A 2 A 1 sin^{-1}\frac {A_2}{A_1} sin−1A1A2在下一部分给出
为什么FMCW相位比传统的FMCW方法具有更高的精度
传统FMCW方法
令 t 1 t_1 t1表示直接路径的达到时间,对应的解调FMCW信号的频率为 f t 1 f_{t_1} ft1;一条达到时间为 t 2 t_2 t2的非直接路径对应的解调FMCW信号的频率为 f t 2 f_{t_2} ft2。当 ∣ f t 1 − f t 2 ∣ < 1 |f_{t_1}-f_{t_2}|<1 ∣ft1−ft2∣<1时,两个峰值在频域内合并成为一个峰值,近似于 ( A 2 f t 2 + A 1 f t 1 ) / ( A 2 + A 1 ) (A_2f_{t_2}+A_1f_{t_1})/(A_2+A_1) (A2ft2+A1ft1)/(A2+A1),其中 A 1 A_1 A1和 A 2 A_2 A2分别是直接路径的振幅和剩余非直接路径的总振幅。因此,频率的错误为:
( A 2 f t 2 + A 1 f t 1 ) / ( A 2 + A 1 ) − f t 1 = ( f t 2 − f t 1 ) / ( 1 + A 1 A 2 ) (A_2f_{t_2}+A_1f_{t_1})/(A_2+A_1)-f_{t_1}=(f_{t_2}-f_{t_1})/(1+\frac{A_1}{A_2}) (A2ft2+A1ft1)/(A2+A1)−ft1=(ft2−ft1)/(1+A2A1)
因此频率误差随 f t 2 − f t 1 f_{t_2}-f_{t_1} ft2−ft1线性增长,并且随 A 1 A 2 \frac{A_1}{A_2} A2A1成比例增加。
使用FMCW相位
假设滤波器后剩余的间接路径的振幅总和比直接路径的振幅低。

如上图所示,蓝色向量表示直接路径,红色向量表示间接路径的总和,绿色向量表示这两个向量之和同时也是接收器上的合成信号。
当红色向量垂直于绿色向量时出现最大相位错误,这对应于相位误差 s i n − 1 ( A 2 A 1 ) sin^{-1}(\frac{A_2}{A_1}) sin−1(A1A2),该误差不依赖于 f t 2 − f t 1 f_{t_2}-f_{t_1} ft2−ft1,并且该误差增长要慢很多。

上图对比了传统峰值检测方法和取FMCW相位方法中误差随 A 2 A 1 \frac{A_2}{A_1} A1A2和 ∣ f t 2 − f t 1 ∣ |f_{t_2}-f_{t_1}| ∣ft2−ft1∣的变化。
通过1D位置进行3D追踪
为了实现3D追踪,使用多个麦克风进行三角测量。使用多个麦克风而不是多个扬声器能够减少能量的消耗同时降低复用多个扬声器的复杂度。
具体来说,我们在矩形的四个角处放置四个麦克风实现3D追踪,其中,两个麦克风处于垂直位置,另外两个麦克风处于水平位置。因此,通过计算所有产生的1D位置的交点,我们可以计算3D位置。
三角测量的准确度依赖于距离麦克风阵列的距离和麦克风之间的间隔。当距离麦克风阵列的距离增加时,3D准确度降低;当麦克风之间的间隔增加时,3D准确度提高。
实际中需要解决的问题
1、相位模糊
我们只能从**解调信号中得到相位模2 π \pi π后的值,即 ϕ ^ ( t ) = ϕ ( t ) % 2 π \hat \phi(t)=\phi(t)\%2\pi ϕ^(t)=ϕ(t)%2π,**这样带来了两个问题:
①在单个chirp中如何检测出任何模2π的偏移,即 ϕ ( t ) \phi(t) ϕ(t)②在每个chirp的开始,如何估计初始的 2 N π 2N\pi 2Nπ相位偏移,即 ϕ ( 0 ) = 2 N π + ϕ ^ ( 0 ) \phi(0)=2N\pi+\hat \phi(0) ϕ(0)=2Nπ+ϕ^(0)
对于第一个问题:
由于带通滤波器,相邻采样之间不会出现超过π的相位差,同时剩余间接路径引起的相位误差以(-π/ 2,π/ 2)为界。因此,当相位模2π后的值在t和 t − δ t t−δt t−δt处的相邻样本之间发生超过π/−π的突然跳变时,此时存在模2π跳变,我们可以通过在计算的相位上加上或减去2π来校正(-π时减去2π,π时加上2π)
对于第二个问题:
使用前一个chirp结束时的距离和速度,这里,通过在10 ms的窗口中对距离值执行最小二乘线性回归来计算瞬时速度,以减少噪声和残留多径的影响。
当前chirp开始时的距离 d ^ s t a r t ( i + 1 ) = d e n d ( i ) + v e n d ( i ) δ T \hat d_{start}^{(i+1)}=d_{end}^{(i)}+v_{end}^{(i)}\delta T d^start(i+1)=dend(i)+vend(i)δT,通过使 ∣ d ( i + 1 ) ( 0 , ϕ ^ ( 0 ) + 2 N π ) − d ^ s t a r t ( i + 1 ) ∣ |d^{(i+1)}(0,\hat \phi(0)+2N\pi)-\hat d^{(i+1)}_{start}| ∣d(i+1)(0,ϕ^(0)+2Nπ)−d^start(i+1)∣最小,我们得到除了 ϕ ^ ( 0 ) \hat\phi(0) ϕ^(0)外的2Nπ偏移。其中:
d ( t , ϕ ( t ) ) = c t d ( t , ϕ ( t ) ) t d ( t , ϕ ( t ) ) 满 足 ϕ ( t ) ≈ − 2 π ( B T t t d + f 0 t d − B 2 T t d 2 ) , 其 中 t d 是 直 接 路 径 的 到 达 时 间 d(t,\phi(t))=ct_d(t,\phi(t))\\t_d(t,\phi(t))满足\phi(t)\approx-2\pi(\frac BTtt_d+f_0t_d-\frac B{2T}t_d^2),其中t_d是直接路径的到达时间 d(t,ϕ(t))=ctd(t,ϕ(t))td(t,ϕ(t))满足ϕ(t)≈−2π(TBttd+f0td−2TBtd2),其中td是直接路径的到达时间
2、时钟同步
我们需要校准的初始相位以及任何由于时钟差异导致的偏移。
开始时,用户使用接收端的麦克风触摸手机扬声器,接收器同时开始记录chirp五秒钟并运行上述跟踪算法。
因为在0距离处,信号有高的SNR,没有运动,间接路径也很少,因此根据FFT结果的峰值估计的距离D是准确的。所以,我们可以根据D,得到使 ∣ D − d ( 0 , ϕ ^ ( 0 ) + 2 N π ) ∣ |D-d(0,\hat\phi(0)+2N\pi)| ∣D−d(0,ϕ^(0)+2Nπ)∣最小的2Nπ,这样就解决了初始相位问题。
最后为了解决由于时钟差异导致的偏移,接收方在5秒内检测到距离测量中的恒定偏移,该偏移与时钟差呈线性关系,通过在接收端消除该测量偏移来补偿时钟差。
3、错误检测和恢复
虽然声音信号可以穿透织物等遮挡物,但对于木材和人体肢体等遮挡物,不同传输介质之间的折射会在直接路径周围产生密集的多径,同时造成直接路径的振幅大大衰减。因此,上述算法因不满足直接路径支配滤波后的解调信号的前提而失败。因此,会产生多个2π相位跟踪误差,导致chirp末端的距离误差大于2cm。当两个chirp之间发声错误时,将导致错误的2Nπ估计,造成后续的chirp误差大于2cm。
为了检测该错误,我们使用麦克风之间的冗余。由于位置不同,所有四个麦克风不太可能同时遇到相同的额外相位误差。因此,如果四个麦克风中的一些麦克风的测量值离群,并且与其他麦克风的测量误差至少为2cm,则表明存在错误。当检测到这种故障时,如果异常仅在一个麦克风中,则接收端补偿2π偏移,直到它在其他三个麦克风的相似范围内为止。如果发生持续错误(这种情况很少发生),我们的算法将退回到FMCW信号的传统峰值估计方法,并会提醒用户。
追踪多台设备
1)一个扬声器追踪多个麦克风阵列
因为信号只能从扬声器发送给麦克风,所以MilliSonic可以支持使用一个智能手机扬声器跟踪附近无限数量的麦克风阵列。因此,单个扬声器可用作信标,以支持对集成了麦克风阵列的多个VR耳机的跟踪。
2)一个麦克风阵列追踪多个基于扬声器的VR设备
使用单个麦克风阵列跟踪多个基于扬声器的VR设备具有挑战性,因为它涉及来自多个智能手机的传输。
传统上,无线系统使用时分多路复用或频分多路复用支持多路并发传输:
①在时分多路复用中,由于每个智能手机扬声器仅允许使用一部分时间,因此它转换为较低的刷新率(实时性实现的不好?),该刷新率与智能手机的数量成反比。
②在频分多路复用中,智能手机上听不见的频率带宽有限并且精度取决于带宽大小,因此是有挑战的。
因为任何两条拥有不同达到时间的FMCW路径具有不同的FFT峰值,因此利用该特性实现多个扬声器的并发传输。我们在每个设备上引入了虚拟的到达时间偏移。开始时,N个扬声器利用时分多路复用传输FMCW chirp,接收方(麦克风阵列)利用MilliSonic算法计算出到达时间,其中第i个扬声器传输信号的到达时间表示为 t d ( i ) t^{(i)}_d td(i),然后通过Wi-Fi连接发送虚拟到达时间偏移给发送方,其中第i个发送方的虚拟达到时间偏移为 i T 2 N − t d ( i ) \frac{iT}{2N}-t^{(i)}_d 2NiT−td(i)。然后, 发 射 方 i 发射方i 发射方i故意将其传输延迟其虚拟偏移量。
这样在接收器处,存在在频域中均匀分布的N个单独的峰值,这对应于N个均匀分布的到达时间,其中第i个到达时间来自第i个发射器。接收方(麦克风阵列)在追踪某个发射方使可以将其他发射方(扬声器)的传输视为多径,由于正交性,它们可以被带通滤波器滤除。 在计算了每个扬声器的信号到达时间之后,它会从中减去虚拟偏移量并获得最终的距离计算。
由于运动,随着时间的流逝,多个扬声器的到达时间可能重合在一起。,这将阻止接收器同时跟踪所有设备。 为了防止这种情况,每当两个设备之间的峰值在FFT域中彼此接近时,接收器就会使用Wi-Fi发送一组新的虚拟延迟。
实现
手机APP: FMCW音频chirp的周期为45ms,频率范围为17.5KHz-23.5KHz,使用安卓手机上开发的APP通过扬声器发送。
麦克风阵列: 使用Arduino Due连接上4个MAX9814麦克风,将这些元件放到20cm×20cm×3cm的纸板上,并将四个麦克风放在纸板一侧的15cm×15cm正方形的四个角上 。同时,也创建了一个6cm×5.35cm×3cm的更小的麦克风阵列。如下图所示:

将Arduino连接上一个Raspberry Pi 3 Model B+处理采样音频数据。
软件使用Scala语言编写,因此既可以运行在Raspberry Pi又可以运行在笔记本电脑上,利用多线程技术来提高性能。该设计中,在Raspberry Pi和笔记本电脑上分别需要40ms和9ms来处理45ms一周期的chirp,因此满足实时性追踪。
4、ApneaApp
参考论文:Contactless Sleep Apnea Detection on Smartphones
ApneaApp是一种非接触式系统,可使用智能手机检测睡眠呼吸暂停事件 。
将手机转变为主动声呐追踪由于呼吸造成的胸部和腹部的运动
FMCW chirp的频率由18kHz线性地增加到20kHz。由于发射频率随时间线性增加,因此与发射信号相比,反射信号中的时间延迟转换为频移。
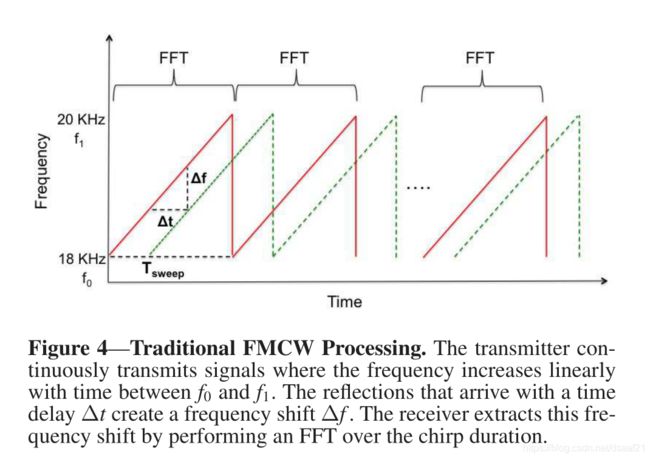
Δ t = 2 d v s o u n d , 其 中 , d 是 手 机 距 离 身 体 的 距 离 , v s o u n d 是 声 音 的 传 播 速 度 Δ f = f 1 − f 0 T s w e e p Δ t \Delta t=\frac{2d}{v_{sound}},其中,d是手机距离身体的距离,v_{sound}是声音的传播速度 \\ \Delta f=\frac{f_1-f_0}{T_{sweep}}\Delta t Δt=vsound2d,其中,d是手机距离身体的距离,vsound是声音的传播速度Δf=Tsweepf1−f0Δt
当存在多个反射物与接收方的距离不同时,它们的反射会转化为信号中不同的频移,通过对一个chirp周期中的信号进行傅立叶变换来提取所有这些频率偏移。 选取的周期 T s w e e p T_{sweep} Tsweep满足在chirp结束之前,期望工作距离内所有点的反射到达。该设计中 T s w e e p = 10.75 m s T_{sweep}=10.75ms Tsweep=10.75ms
挑战: 呼吸动作微小,产生很小的频移,2cm的呼吸位移仅产生11.7 Hz的频移;根据该设计的采样率和chirp周期,FFT峰值为93.75Hz,远比呼吸造成的频移大。
为了解决上述问题,ApneaApp接收器对N个FMCW线性调频脉冲执行傅立叶变换。
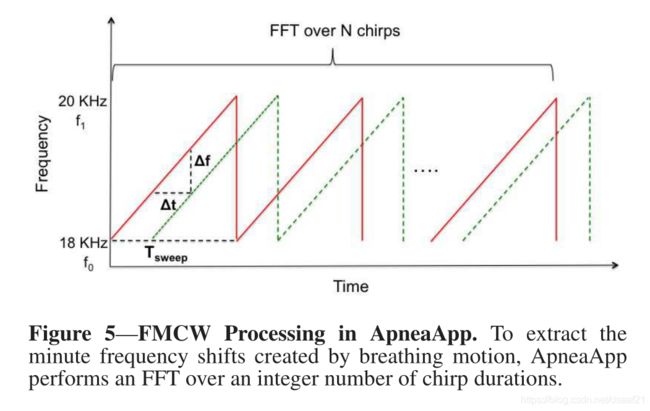
在该设计中,N=10,因此,FFT的峰值为9.37Hz,这使我们能够捕获呼吸运动引起的微小频移。
剩余部分不太明白了,欢迎指点
5、LLAP
参考论文:Device-Free Gesture Tracking Using Acoustic Signals
测量1D相对距离变化
首先,我们使用相干检测器将接收到的声音信号下变频为复数基带信号。其次,我们根据基带信号的相位变化来测量路径长度的变化。第三,我们结合不同频率的相位变化来减轻多径效应。
LLAP概述
LLAP使用连续波 A c o s ( 2 π f t ) Acos(2\pi ft) Acos(2πft),f在17$\backsim$23kHz的范围内,利用商用移动设备发送,同时利用相同设备上的麦克风录制,采样率为48kHz。由于接收到的声波是由同一个设备传输的,因此发送方和接收方之间没有载波频率偏移(CFO)。因此,我们可以使用传统的相干检波器结构,如下图所示,将接收到的声音信号下变频为基带信号。

接收信号首先被分成两个相同的副本,并与发射信号 c o s 2 π f t cos 2πft cos2πft及其 − s i n 2 π f t −sin 2πft −sin2πft相乘;然后,利用级联积分梳状(CIC)滤波器去除高频分量,抽取信号,得到相应的同相和正交信号。
声音信号降频变换
CIC滤波器是一个三段滤波器,抽取比为16,差分延迟为17。下图展示了该CIC滤波器的频率响应
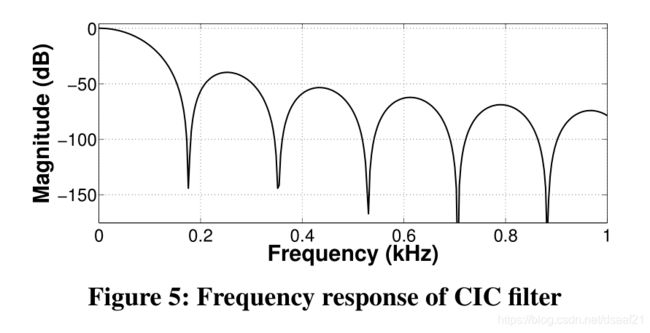
我们选择参数,以使滤波器的第一个零和第二个零出现在175 Hz和350 Hz处。该CIC滤波器的通带为0~100Hz。滤波器的第二个零出现在350Hz,因此( f ± 350 f\pm350 f±350)Hz的信号将被衰减超过120dB。因此,为了使来自相邻频率的干扰最小,当扬声器同时传输多个频率时,我们使用350 Hz的频率间隔。为了获得更好的计算效率,我们在CIC之后不使用频率补偿FOR滤波器。
CIC过滤器仅涉及加法和减法,计算开销较低。 因此,降频变换过程中,每个采样点只需要两个乘法(将接受信号与 c o s 2 π f t cos 2πft cos2πft和 − s i n 2 π f t −sin 2πft −sin2πft相乘)。在降频变换之后,采样率下降到了3kHz,以提高后续信号处理效率。
为了理解数字降频变换的过程,我们考虑声音信号经过路径p,该路径长度为 d p ( t ) d_p(t) dp(t)。经过路径p的接收信号表示为: R p ( t ) = 2 A p ′ c o s ( 2 π f t − 2 π f d p ( t ) / c − θ p ) R_p(t)=2A'_pcos(2\pi ft-2\pi fd_p(t)/c-\theta_p) Rp(t)=2Ap′cos(2πft−2πfdp(t)/c−θp),其中, 2 A p ′ 2A'_p 2Ap′为接收信号的振幅,项 2 π f d p ( t ) / c 2\pi f d_p(t)/c 2πfdp(t)/c是由传播延迟 τ p = d p ( t ) / c \tau_p=d_p(t)/c τp=dp(t)/c造成的相位滞后,c为声音的传播速度, θ p \theta_p θp为由于硬件延迟和反射引起的相位反转造成的初始相位。
将接受信号和 c o s ( 2 π f t ) cos(2\pi ft) cos(2πft)相乘得:
2 A p ′ c o s ( 2 π f t − 2 π f d p ( t ) / c − θ p ) × c o s ( 2 π f t ) = A p ′ ( c o s ( − 2 π f d p ( t ) / c − θ p ) + c o s ( 4 π f t − 2 π d p ( t ) / c − θ p ) ) 2A'_pcos(2\pi ft-2\pi fd_p(t)/c-\theta_p)\times cos(2\pi ft)=A'_p(cos(-2\pi fd_p(t)/c-\theta_p)+cos(4\pi ft-2\pi d_p(t)/c-\theta_p)) 2Ap′cos(2πft−2πfdp(t)/c−θp)×cos(2πft)=Ap′(cos(−2πfdp(t)/c−θp)+cos(4πft−2πdp(t)/c−θp))
第二项拥有高频2f,能被低通CIC滤波器滤除。因而,得到基带信号的I分量 I p ( t ) = A p ′ ( c o s ( − 2 π f d p ( t ) / c − θ p ) I_p(t)=A'_p(cos(-2\pi fd_p(t)/c-\theta_p) Ip(t)=Ap′(cos(−2πfdp(t)/c−θp)。相似地,得到基带信号的Q分量 Q p ( t ) = A p ′ s i n ( − 2 π f d p ( t ) / c − θ p ) Q_p(t)=A'_psin(-2\pi fd_p(t)/c-\theta_p) Qp(t)=Ap′sin(−2πfdp(t)/c−θp)
将这两部分分别作为实部和虚部得到复信号 B p ( t ) = A p ′ e − j ( 2 π f d p ( t ) / c + θ p ) , 其 中 j 2 = − 1 B_p(t)=A'_pe^{-j(2\pi fd_p(t)/c+\theta_p)},其中j^2=-1 Bp(t)=Ap′e−j(2πfdp(t)/c+θp),其中j2=−1
因此,路径p对应的相位 ϕ p ( t ) = − ( 2 π f d p ( t ) / c + θ p ) \phi_p(t)=-(2\pi fd_p(t)/c+\theta_p) ϕp(t)=−(2πfdp(t)/c+θp),当 d p ( t ) d_p(t) dp(t)改变波长 λ = c / f \lambda=c/f λ=c/f时,相位改变2 π \pi π。
基于相位的路径长度测量
我们需要将基带信号分解为静态和动态向量。其中,静态向量对应于直线传播或被静态物体反射的声波,它比由手反射来的声波强度更大;动态向量对应于由移动的手反射来的声波。将静态向量与动态向量分离是有挑战的。
论文中使用了一种启发式算法称作局部极值检测Local Extreme Value Detection(LEVD)来估计静态向量。该算法分别对I / Q分量进行操作,以估计静态矢量的实部和虚部。该算法由经验模态分解算法Empirical Mode Decomposition(EMD)启发得到。
我们首先找到替代的局部最大值和最小值点,它们的差值大于经验阈值 T h r Thr Thr,该阈值被设置为静态环境中基带信号标准偏差的三倍。然后,使用相近的两个局部最大值和最小值的平均值作为静态向量的估计值。
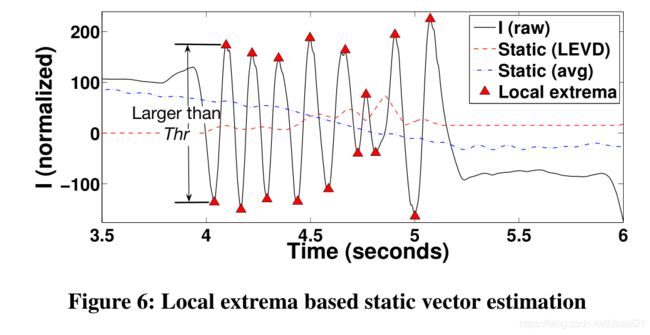
在使用LEVD找到静态向量之后,我们从基带信号中减去它以获得动态向量。然后,使用动态向量的相位 ϕ d ( t ) \phi_d(t) ϕd(t)来得到路径长度的改变。在0~t时间内,路径长度的变化为:
d ( t ) − d ( 0 ) = − ϕ d ( t ) − ϕ d ( 0 ) 2 π × λ d(t)-d(0)=-\frac{\phi_d(t)-\phi_d(0)}{2\pi}\times \lambda d(t)−d(0)=−2πϕd(t)−ϕd(0)×λ
其中,d(t)是扬声器通过手反射到麦克风的路径长度, λ = c / f \lambda=c/f λ=c/f是声音的波长,
当手、麦克风、扬声器在同一条直线上时,手的移动距离为 ( d ( t ) − d ( 0 ) ) / 2 (d(t)-d(0))/2 (d(t)−d(0))/2
减轻多径效应
如果声波传播的路径长度不随手的移动而变化,则称为静态路径;如果声波传播的路径长度随手的移动而变化,则称为动态路径。一个动态路径示例是从扬声器到手,然后到附近的桌子,最后到麦克风。 因此,有时会存在多个动态矢量,并且这些动态矢量可能具有不同的相位,这将导致复杂的信号轨迹。 由于存在动态多径,因此很难根据叠加的动态向量确定实际的相位变化。
我们利用多个频率来减轻多径效应。 不同声音频率的波长是不同的。因此,同一多径分量在不同频率下的相位不同,不同频率下的相位变化也不同。不同频率的动态矢量是同一组动态路径在不同相位偏移下的组合。由于多径分量在不同频率下的组合不同,因此我们可以将从不同频率获得的测量值进行组合以减轻多径效应。
为了得到不同频率的基带信号,我们同时传输多个频率的声音。相干检测结构可应用于每个频率以获得每个频率的一个复基带信号。通过仔细选择CIC滤波器的参数和频率间隔,消除了相邻频率间的干扰。因此,可以独立地测量每个频率。在得到不同频率下动态矢量的相位后,利用每个频率对应的波长得到距离随时间的变化曲线。我们使用线性回归将不同频率的结果结合起来。首先,当没有多径效应时,所有频率的测量距离变化应该相同。其次,距离应在短时间内线性变化,例如10 ms,因为在短时间内移动速度几乎恒定。因此,我们使用线性回归来寻找适合所有从不同频率得到的距离变化曲线的最佳直线。 对于多径效应导致距离估计结果异常的频率,回归误差较大。因此,我们去除回归误差较大的频率,使用剩余的频率以获得更好的线性回归结果。
测量2D绝对距离
我们首先使用基于延迟分布的方法来确定绝对路径长度,以便获得粗粒度的手初始位置。然后,我们结合粗粒度的手初始位置和细粒度的路径长度变化,以实现二维跟踪。
基于延迟分布的绝对路径测量
这一部分不太明白,欢迎指点!
上一节中的方法仅用于测量路径长度改变,对于2D追踪来说是不充分的,由于如下两个原因:
首先,由于缺乏初始位置,我们不能仅利用路径长度的变化来确定运动方向。路径长度的变化由运动距离和相对于麦克风与扬声器的运动方向决定。即使对象移动相同的距离,垂直于扬声器与麦克风连线的运动与平行于该连线的运动造成的路径长度的改变是不同的。其次,路径长度变化中的测量误差会随着时间累积。 因此,即使我们知道初始的手的位置,经过长时间的跟踪,路径长度估计也会偏移。
本文提出了一种基于时延分布的粗粒度绝对路径长度估计方法。该方法利用未经调制的连续波声信号来避免传统测距信号引入的突发脉冲等可闻噪声。虽然粗粒度测量的精度较低,约为4cm,但它很好地用于提供初始位置,因为一旦给定初始位置,就可以通过精确到mm级的细粒度路径长度变化测量进行实时跟踪。
为了测量绝对路径长度,发送N个不同频率的声音信号, f k = f 0 + k Δ f , k = 0 , 1 , . . . , N − 1 f_k=f_0+k\Delta f,k=0,1,...,N-1 fk=f0+kΔf,k=0,1,...,N−1。因此,当频率为 f k f_k fk时,任意路径p的基带信号为:
B p ( k , t ) = A p . k ′ e − j ( 2 π ( f 0 + k Δ f ) d p ( t ) / c + θ p , k ) B_p(k,t)=A'_{p.k}e^{-j(2\pi(f_0+k\Delta f)d_p(t)/c+\theta_{p,k})} Bp(k,t)=Ap.k′e−j(2π(f0+kΔf)dp(t)/c+θp,k)
对于给定的 d p ( t ) d_p(t) dp(t)的路径长度,不同频率的基带信号的相位作为Δf的线性函数减小。因此, B p ( k , t ) B_p(k,t) Bp(k,t)在给定时间t将沿频率轴(改变k的值)具有恒定的相位变化。如果我们对 B p ( k , t ) B_p(k,t) Bp(k,t)进行离散傅里叶逆变换:
b p ( n , t ) = 1 N ∑ k = 0 N − 1 B p ( k , t ) e j 2 π k n / N , n = 0 , . . . , N − 1 b_p(n,t)=\frac1N\sum_{k=0}^{N-1}B_p(k,t)e^{j2\pi kn/N},n=0,...,N-1 bp(n,t)=N1k=0∑N−1Bp(k,t)ej2πkn/N,n=0,...,N−1
假设通过设置 A p , k ′ 和 θ p , k A'_{p,k}和\theta_{p,k} Ap,k′和θp,k 忽略 A p , k ′ 和 θ p , k A'_{p,k}和\theta_{p,k} Ap,k′和θp,k的变化,那么,对于 n ^ ∈ [ 0 , N − 1 ] , d p ( t ) = n ^ c / ( N Δ f ) \hat n\in[0,N-1],d_p(t)=\hat nc/(N\Delta f) n^∈[0,N−1],dp(t)=n^c/(NΔf)的情况下, b p ( n , t ) = A p ′ e − j 2 π f 0 d p ( t ) / c × δ ( n − n ^ , t ) , 其 中 δ ( n , t ) 是 单 位 冲 击 函 数 , δ ( n , t ) = { 1 n = 0 0 其 他 b_p(n,t)=A'_pe^{-j2\pi f_0d_p(t)/c}\times\delta(n-\hat n,t),其中\delta(n,t)是单位冲击函数,\delta(n,t)=\begin{cases}1&n=0\\0&其他\end{cases} bp(n,t)=Ap′e−j2πf0dp(t)/c×δ(n−n^,t),其中δ(n,t)是单位冲击函数,δ(n,t)={10n=0其他
B p ( k , t ) 的 I D F T 结 果 b p ( n , t ) 是 路 径 p 的 时 延 分 布 B_p(k,t)的IDFT结果b_p(n,t)是路径p的时延分布 Bp(k,t)的IDFT结果bp(n,t)是路径p的时延分布,在 n ^ = N d p ( t ) Δ f / c \hat n=Nd_p(t)\Delta f/c n^=Ndp(t)Δf/c时拥有单一峰值。因此,使 b p ( n , t ) 最 大 的 n ^ b_p(n,t)最大的\hat n bp(n,t)最大的n^表示了路径p的时延。
因为通过LEVD算法将静态向量移除了,所以动态向量的IDFT仅包含移动目标的时延分布。我们可以通过得到 b p ( n , t ) b_p(n,t) bp(n,t)的峰值,每个峰值对应一条由移动目标造成的路径,由此计算出相应目标的路径长度。
参数设置
基于时延分布地测量方法存在两个参数需要被谨慎地选择:频率间隔 Δ f \Delta f Δf和频率的数量N。
Δ f \Delta f Δf:一方面, Δ f \Delta f Δf需要设置得足够大才能区分开在载波频率内的高速运动;另一方面, Δ f \Delta f Δf又需要设置得足够小才能避免时域混叠。估计的峰值位置 n ^ \hat n n^是整数模N得到的结果,范围为0 ∽ \backsim ∽N-1;因此,反射路径长度为d的时延分布情况与反射路径长度为 d + m c / Δ f ( m 为 整 数 ) d+mc/\Delta f(m为整数) d+mc/Δf(m为整数)的时延分布情况相同。因为该实验中目标是小于50 cm的工作范围,所以设置 Δ f = 350 H z \Delta f=350Hz Δf=350Hz.
N:一方面,更大的N给出了更好的距离分辨率;另一方面,更大的N需要更高的带宽并且减少了我们可以在单频中传输的能量。因为对于N的总带宽为 ( N − 1 ) Δ f (N-1)\Delta f (N−1)Δf,并且我们只有有限可用频率范围(17~23kHz),在该论文中,N=16。
系统校准
初始相位偏移 θ p , k \theta_{p,k} θp,k又两种原因造成:
第一种是反射引起的相位反转,对于所有频率都是相同的;
第二种是由于移动设备的硬件限制而导致音频播放和录制过程的延迟 ,这因设备型号不同而异。由于存在该延迟,我们将CW传输到扬声器的时间与相干检测器中用于乘法的参考cos(2πft)信号不一致。 因此,发射信号和接收信号之间存在一个随机的Δt偏移。这造成了在对 b p ( n , t ) b_p(n,t) bp(n,t)进行IDFT后存在时间偏移 Δ t \Delta t Δt,该时间偏移取决于音频初始化过程,在系统开始发射和接收连续信号后,它将保持恒定。
对于第二种情况,我们在系统开始发出声音信号后执行时间偏移校准。由于硬件/操作系统对所有路径引入的时间偏移Δt均相同,因此在校准过程中,我们将直线路径(LOS) 用作参考路径。因为我们知道扬声器和麦克风之间的确切路径,因此我们计算直线路径(LOS) 的 n ^ L O S \hat n_{LOS} n^LOS。在没有大的反射物时,静态向量由LOS控制,如果我们对不同频率的静态向量进行IDFT时,在 Δ t = 0 \Delta t=0 Δt=0时,预计最高峰出现在 n ^ L O S \hat n_{LOS} n^LOS处。如果我们观察到峰值不在 n ^ L O S \hat n_{LOS} n^LOS处,那么就对参考cos(2πft)信号引入 Δ t ′ \Delta t' Δt′的延迟,然后反复调整∆t的值,直到峰值出现在预期位置。
将细粒度的相位测量和粗粒度的时延测量结合
基于相位的测量方法提供准确和实时的距离变化信息,因此系统可以根据用户的运动提供高准确率和低时延。
基于时延分布地测量方法提供绝对路径长度估计,因此相位测量中的误差就不会随时间累积。
将这两种方法结合可以实现低时延和稳定的测量。仅当 b p ( n , t ) b_p(n,t) bp(n,t)中存在一个归一化能量高于给定阈值的主峰时,我们才使用基于延迟分布的路径长度估计。在该情况下,使用指数滑动平均Exponential Moving Average(EMA)算法通过相位测量追踪路径长度,从而加强通过延迟分布获得的路径长度估计。如果手部反射弱并且在 b p ( n , t ) b_p(n,t) bp(n,t)中不存在主峰,仅使用基于相位改变的方法来更新路径长度。
2D手势追踪
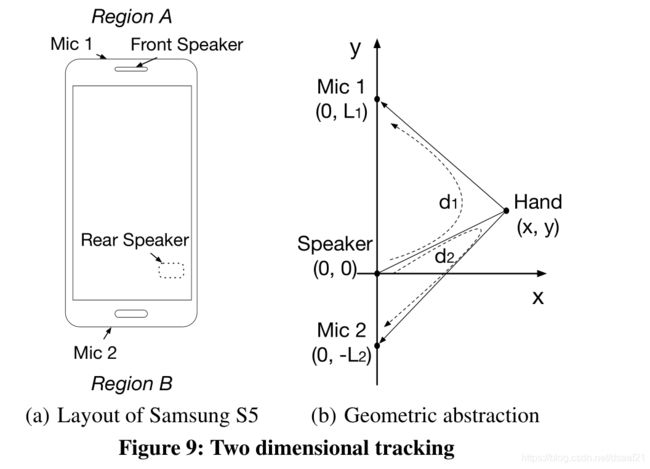
为了测量多个扬声器/麦克风的路径长度,我们使用了许多移动设备上可用的立体声播放和录音功能。例如,我们可以在位于不同位置的两个麦克风处记录声音,以同时获得两个路径测量值。当有多个扬声器时,我们可以通过为每个扬声器分配不同的频率来将信号与其他扬声器分开。
为了简化讨论,考虑一个有一个扬声器和两个麦克风的手机,如上图。扬声器放置在原点,两个麦克风分别位于 ( 0 , L 1 ) 和 ( 0 , − L 2 ) (0,L_1)和(0,-L_2) (0,L1)和(0,−L2)。假设扬声器通过手到两个麦克风的路径长度为d1和d2。手的坐标 ( x , y ) (x,y) (x,y)由椭圆函数表示为:
4 x 2 d 1 2 − L 1 2 + 4 ( y − L 1 / 2 ) 2 d 1 2 = 1 4 x 2 d 2 2 − L 2 2 + 4 ( y + L 2 / 2 ) 2 d 2 2 = 1 \frac{4x^2}{d_1^2-L_1^2}+\frac{4(y-L_1/2)^2}{d_1^2}=1\\ \frac{4x^2}{d_2^2-L_2^2}+\frac{4(y+L_2/2)^2}{d_2^2}=1 d12−L124x2+d124(y−L1/2)2=1d22−L224x2+d224(y+L2/2)2=1
解得:
x = ( d 1 2 − L 1 2 ) ( d 2 2 − L 2 2 ) ( ( L 1 + L 2 ) 2 − ( d 1 − d 2 ) 2 ) 2 ( d 1 L 2 + d 2 L 1 ) y = d 2 L 1 2 − d 1 L 2 2 − d 1 2 d 2 + d 2 2 d 1 2 ( d 1 L 2 + d 2 L 1 ) x=\frac{\sqrt{(d_1^2-L_1^2)(d_2^2-L_2^2)((L_1+L_2)^2-(d_1-d_2)^2)}}{2(d_1L_2+d_2L_1)}\\ y=\frac{d_2L_1^2-d_1L_2^2-d_1^2d_2+d_2^2d_1}{2(d_1L_2+d_2L_1)} x=2(d1L2+d2L1)(d12−L12)(d22−L22)((L1+L2)2−(d1−d2)2)y=2(d1L2+d2L1)d2L12−d1L22−d12d2+d22d1
2D追踪算法的伪代码如下:

实现
android平台:我们使用Android NDK将大多数信号处理算法实现为C函数,以实现更高的效率。我们的实现是一个可以实时绘制二维手部轨迹的APP。
IOS平台:我们使用vDSP加速框架,该框架可实现比Android平台更好的计算效率。 但是,iOS平台仅支持单通道录制,因此,仅仅实现了1D手部追踪在IOS平台上。

先用手机的硬件和操作系统存在一些限制:
首先,麦克风和扬声器的位置并未针对手势跟踪进行优化。如Figure 9(a)所示,当手位于Region A时,由Mic1获得的反射信号非常好而Mic2仅接收到很弱的反射信号。因此,为了获得两个麦克风的强信号,我们的二维跟踪实验是在使用前后扬声器时在手机的前面或后面进行的,而不是在区域A或B。
其次,我们系统的延迟受操作系统限制。我们在android实现中选择512个样本的数据段大小,当采样率为48 kHz时,持续时间为10.7 ms。在IOS上仅需要32个样本数据,但是,iOS系统仅支持通过单个麦克风进行录音,因此我们未在iOS平台上实现2-D跟踪。
6、C-FMCW
参考论文:C-FMCW Based Contactless Respiration Detection Using Acoustic Signal
传统FMCW方法的理论范围分辨率上限
发射信号 v t x v_{tx} vtx具有频率1/T的所有倍数的基频。如果忽略振幅衰减并假设目标是静止的或者移动缓慢,那么接收信号 v r x v_{rx} vrx是发射信号的时移版本,因此发射信号 v t x v_{tx} vtx和接收信号 v r x v_{rx} vrx拥有相同的基频。因此, v m = v t x ⋅ v r x v_m=v_{tx}\cdot v_{rx} vm=vtx⋅vrx具有频率1/T的所有倍数的基频,这意味着在频率内, v m v_m vm仅在1/T Hz具有频谱点。即,混合信号的频率分辨率 δ f ≥ 1 / T \delta f≥1/T δf≥1/T。
根据公式,传统FMCW方法的理论范围分辨率为: δ R = C T 2 B δ f b \delta R=\frac{CT}{2B}\delta f_b δR=2BCTδfb
上式表明, δ R \delta R δR依赖于混合信号的频率分辨率 δ f b \delta f_b δfb。 δ f b \delta f_b δfb受chirp频率1/T限制。因此,传统FMCW方法的理论范围分辨率上限为:
δ R ≥ C T 2 B ⋅ 1 T = C 2 B \delta R≥\frac{CT}{2B}\cdot\frac 1T=\frac C{2B} δR≥2BCT⋅T1=2BC
上式表明,线性调频FMCW的距离分辨率取决于扫描带宽B。较窄的带宽导致较低的距离分辨率。
Cross-correlation function based FMCW(C-FMCW)
距离估计的目的是测量时延 τ \tau τ,对于周期为T的发送信号,利用发射信号和接收信号互相关的主峰,可以测量T/2内的时延,因此提出了基于互相关函数的FMCW(Cross-correlation function based FMCW)。
互相关函数定义为:
R ( n ) = { 1 N − n ∑ m = 0 N − n − 1 v t x ( m ) ⋅ v r x ( m + n ) , n ≥ 0 1 N − ∣ n ∣ ∑ m = 0 N − ∣ n ∣ − 1 v r x ( m ) ⋅ v t x ( m + n ) , n < 0 R(n)=\begin{cases} \frac 1{N-n}\sum_{m=0}^{N-n-1}v_{tx}(m)\cdot v_{rx}(m+n),&n\geq 0\\ \frac 1{N-|n|}\sum_{m=0}^{N-|n|-1}v_{rx}(m)\cdot v_{tx}(m+n),&n<0 \end{cases} R(n)={N−n1∑m=0N−n−1vtx(m)⋅vrx(m+n),N−∣n∣1∑m=0N−∣n∣−1vrx(m)⋅vtx(m+n),n≥0n<0
其中,N是发射信号一个周期T内的样本数, n = − N + 1 , − N + 2 , . . . , N − 1 n=-N+1,-N+2,...,N-1 n=−N+1,−N+2,...,N−1
R ( n ) R(n) R(n)测量发送信号 v t x v_{tx} vtx与接收信号 v r x v_{rx} vrx的n样本移位版本的相似度。
假设R(n)在Lag移位后达到他的峰值R(Lag)。因为 v r x v_{rx} vrx是 v t x v_{tx} vtx带振幅衰减的移位版本,意味着 v r x v_{rx} vrx与 v t x v_{tx} vtx经过Lag个采样点移位后重叠,因此我们可以通过计算样本的数量来测量到达时间。
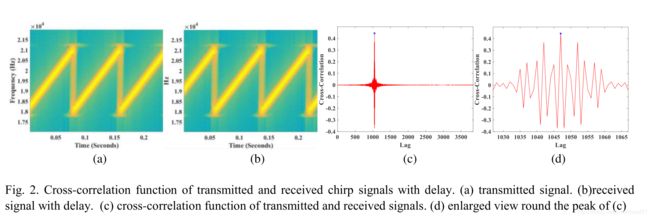
Fig 2(a)和Fig 2(b)分别是3个周期的发送和接收信号,接收信号是发送信号移位1047个采样点的版本。Fig 2©表示了发送信号和接收信号的互相关R(n),根据R(n)的定义,峰值R(Lag)=R(1047)。Fig 2(d),可以得到峰值出现在n=1047上。
时延 τ = L a g F s , F s 是 采 样 率 \tau=\frac{Lag}{F_s},F_s是采样率 τ=FsLag,Fs是采样率
发送方和目标之间的距离R如下计算:
{ τ = L a g / F s τ = 2 ( R + v t ) / C = > R = C ⋅ L a g 2 F s − v t \begin{cases} \tau=Lag/F_s\\ \tau=2(R+vt)/C \end{cases}=> R=\frac{C\cdot Lag}{2F_s}-vt {τ=Lag/Fsτ=2(R+vt)/C=>R=2FsC⋅Lag−vt
当目标静止或者移动速度很慢(very slowly)时,v接近于0, 因此 R = C ⋅ L a g 2 F s R=\frac{C\cdot Lag}{2F_s} R=2FsC⋅Lag
该论文要求目标静止或者移动速度,因此不用进行一般的acoustic motion tracking,观看论文自带的视频链接发现,运动过程中,测距误差很大
