《PyTorch深度学习实践》学习笔记：处理多维特征的输入

---

一、多维特征计算

pytorch提供的sigmoid函数是一种向量函数。也就是说torch.exp([x1 x2 x3]) = [e^x1 e^x2 e^x3]

采用Mini-Batch的形式可以将方程运算转换矩阵的运算。转化的原因是向量化的运算可以利用计算机GPU/CPU的并行运算的能力来提高整个运算的速度。如果使用for循环来写这种运算，计算是相当慢的。

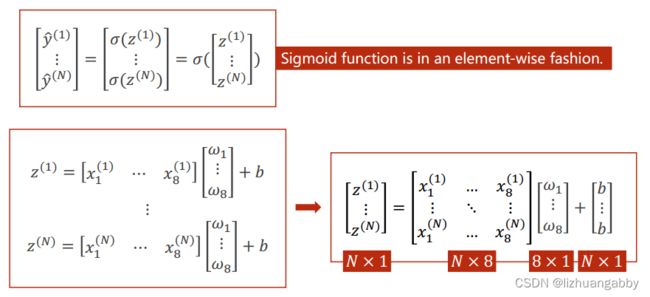
此时我们可以编写这个向量运算的模型代码：

class Model(nn.Module):
    def __init__(self):
        super(Logisticmodel, self).__init__()
        self.linear = nn.Linear(8,1)      # 只需要修改这里的维度就变成了多维计算
 
    def forward(self,x):
        y_pred = self.linear(x)
        y_pred = torch.sigmoid(y_pred)
        return y_pred	
model = Model()

上述我们是通过一层的网络，实现了8-D到1-D的转变，我们还可以通过多层网络实现从8D-1D，比如我们可以8D-6D-2D-1D这样多层网络实现。对于多层网络的计算，本质上还是通过矩阵的运算实现。对于实际问题中具体每一层网络的参数怎么设置，这是一个超参数搜索的问题，通过不断地尝试去发现哪个参数在测试集上表现的好。

神经网络的本质：就是寻找一种最优的非线性的空间变换函数。而这种非线性的空间变换函数是通过多个线性变换层，通过找到最优的权重，组合起来的模拟的一种非线性的变化。

其中在网络的中间会使用Sigmoid函数，因为激活函数（Sigmoid函数）可以将线性变换增加一些非线性的因子，这样我们就可以拟合一些非线性的变换。（如果每一层的神经网络只是不断的叠加线性函数的话，最终的函数还会只是一个线性函数。）

(神经网络并不是学习能力越强越好，学习能力太强，会学习数据集中的一些噪声，并不利于优化模型，学习的太强会导致过拟合，从而可以看到泛化能力弱。）

---

二、处理糖尿病数据集分类

数据集：

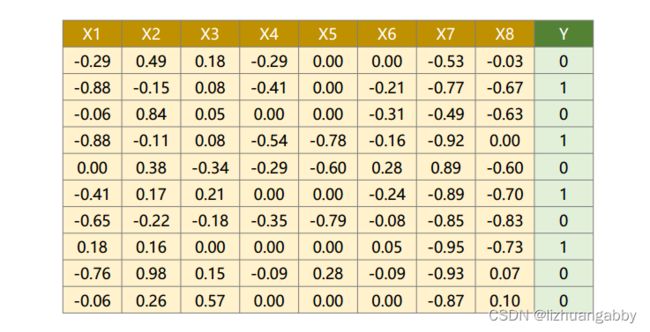
其中X1-X8代表糖尿病的一系列指标，Y代表一年后糖尿病是否会加重。

糖尿病数据集：提取链接 提取码: dpfj

1. 接下来首先应该读取数据集中的数据:

xy =  np.loadtxt('diabetes.csv.gz',delimiter=',',dtype=np.float32)
x_data = torch.from_numpy(xy[:,:-1])   # 所有行除最后一列
y_data = torch.from_numpy(xy[:,[-1]])  # 所有行最后一列
print(x_data.type())

此时准备好了数据集，torch.FloatTensor类型。

2.接下来准备模型：

class Model(nn.Module):
    def __init__(self):
        super(Model, self).__init__()
        self.linear1 = nn.Linear(8,6)
        self.linear2 = nn.Linear(6,4)
        self.linear3 = nn.Linear(4,1)
        self.sigmoid = nn.Sigmoid()
    def forward(self,x):
        x = self.sigmoid(self.linear1(x))
        x = self.sigmoid(self.linear2(x))
        x = self.sigmoid(self.linear3(x))
        return x
model = Model()        # 实例化一个模型

3. 准备损失函数和优化器：

损失函数还是一个二分类的问题，所以还是使用BCEloss即可；对于优化器，我们还是可以采用SGD优化器。

# 损失函数和优化器
creation = nn.BCELoss(reduction='mean')  # 上图中设置size_average=True的方式现在已弃用
optimizer = torch.optim.SGD(model.parameters(),lr=0.01)

3. 训练过程：

for epoch in range(1000):
    # 前馈计算
    y_pred = model(x_data)
    # 计算loss
    loss = creation(y_pred,y_data)
    print(epoch+1,loss.item())
    # 反馈运算
    optimizer.zero_grad() # 梯度先清0
    loss.backward()
    optimizer.step()      # 梯度更新

    epoch_list.append(epoch)
    loss_list.append(loss.item())

---

三、完整代码

import torch
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt

# 数据集
xy =  np.loadtxt('diabetes.csv.gz',delimiter=',',dtype=np.float32)
x_data = torch.from_numpy(xy[:,:-1])  # 所有行除最后一列
y_data = torch.from_numpy(xy[:,[-1]])  # 所有行最后一列
print(x_data.type())

# 模型
class Model(nn.Module):
    def __init__(self):
        super(Model, self).__init__()
        self.linear1 = nn.Linear(8,6)
        self.linear2 = nn.Linear(6,4)
        self.linear3 = nn.Linear(4,1)
        self.sigmoid = nn.Sigmoid()
    def forward(self,x):
        x = self.sigmoid(self.linear1(x))
        x = self.sigmoid(self.linear2(x))
        x = self.sigmoid(self.linear3(x))
        return x
model = Model()        # 实例化一个模型

# 损失函数和优化器
creation = nn.BCELoss(reduction='mean')
optimizer = torch.optim.SGD(model.parameters(),lr=0.01)

# 训练
epoch_list = []
loss_list = []
for epoch in range(1000):
    # 前馈计算
    y_pred = model(x_data)
    # 计算loss
    loss = creation(y_pred,y_data)
    print(epoch+1,loss.item())
    # 反馈运算
    optimizer.zero_grad() # 梯度先清0
    loss.backward()
    optimizer.step()      # 梯度更新

    epoch_list.append(epoch)
    loss_list.append(loss.item())

# 画图
plt.plot(epoch_list,loss_list)
plt.xlabel("epoch")
plt.ylabel("loss")
plt.show()

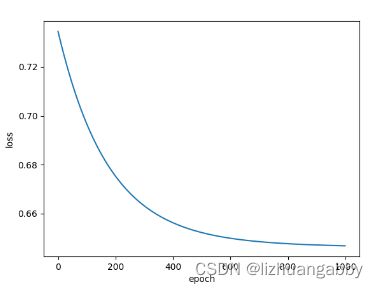
运行结果：

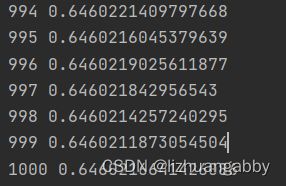
loss下降曲线：

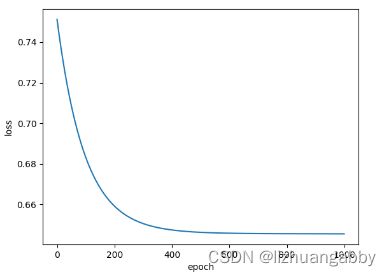
可以修改一个激活函数，看一下不同的训练效果：

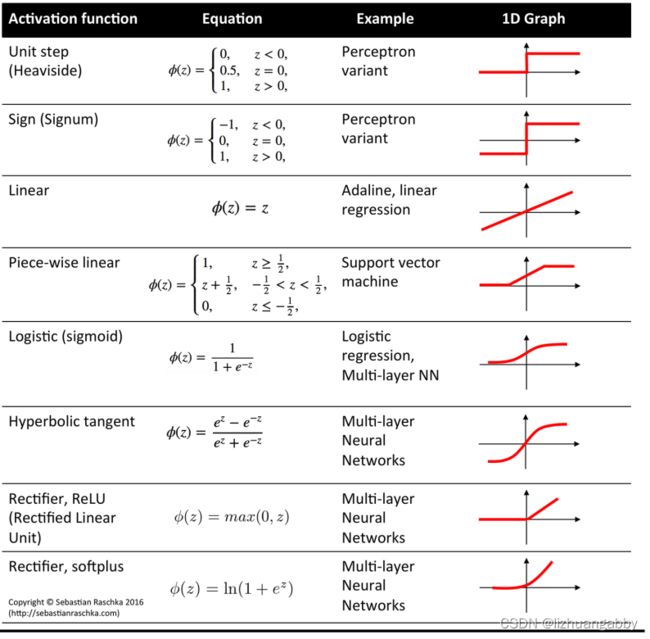
我们一般会在中间的层使用一个ReLU激活函数，但是最后一个线性层一般还是采用sigmoid函数，因为Relu函数小于0的部分都是0，计算log的时候会有问题，而sigmoid函数还是相对平滑的。

下面以Relu激活为例，观察loss变化：

class Model(nn.Module):
    def __init__(self):
        super(Model, self).__init__()
        self.linear1 = nn.Linear(8,6)
        self.linear2 = nn.Linear(6,4)
        self.linear3 = nn.Linear(4,1)
        self.activate1 = nn.ReLU()
        self.activate2 = nn.Sigmoid()
    def forward(self,x):
        x = self.activate1(self.linear1(x))
        x = self.activate1(self.linear2(x))
        x = self.activate2(self.linear3(x))
        return x
model = Model()        # 实例化一个模型

对比之前的loss函数，可以看出Relu函数下降的相对缓慢，拐弯的地方出现的相对靠后一点，但总体loss下降的值跟sigmoid相差不大。

改变激活函数为softplus，观察loss曲线：

该激活函数的loss下降比sigmoid的还快，拐点出现的更早。

pytorch提供的激活函数很多，可以去pytroch的官网查看各个激活函数的细节，对于激活函数的使用，也是一个不断探索的过程：
https://pytorch.org/docs/stable/nn.html#non-linear-activations-weighted-sum-nonlinearity