区间DP(总结)

　　学长一晚上的耐心讲解，使我明白区间DP这么高级的东西，还是挺容易的。也就是在一段区间内的动态规划。

　　下面用例题进行总结。

　　例题:石子归并。

　　描述 有N堆石子排成一排，每堆石子有一定的数量。现要将N堆石子并成为一堆。合并的过程只能每次将相邻的两堆石子堆成一堆，并将新的一堆石子数记为该次合并的得分。

　　给组测试数据 

　　　　　输入　　　4　　　　表示有4堆石子

　　　　　  4 4 5 9　　表示每堆石子的个数

　　　　　输出  54         表示最大的得分　　　

　　分析:主要思想就是一个一个累加：4 4 5 9 先看下去是我想知道dp[i][j]的最大值，i表示起始位置，j表示终止位置，所以我肯定是想求出dp[1][4]间的最大值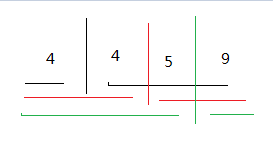但是我从1到4可是如图这三种截取方法，所以我先从小的开始记录。

dp[1][1]=4;dp[2][2]=4;dp[3][3]=5;dp[4][4]=9。然后我在长度为2的时候记录，dp[1][2]=4+4=8,dp[2][3]=8+5=14;dp[3][4]=14+9=23;这样加起来的值就是8+14+23=45；但是如果我反过来呢？dp[1][2]=5+9=14;dp[2][3]=14+4=18;dp[3][4]=18+4=22;这样加起来的值就是14+18+22=54。很明显，54就是所求的最大值。

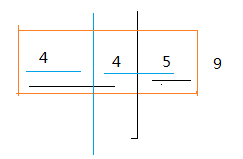如图，如果我相求圈着的这个三个的值，我完全可以有图上这两种分割，并且分割出来的值是已经知道的了。

动态规划的思想：先两两合并，在三三合并，最后再NN合并，在合并过程中，较大的区间可以拆分成已经的小区间进行计算，省时又省力。比如，我可以在三三合并的时候可以拆分成一一还有二三相加。即把当前阶段的合并方法细分成前一阶段已计算出的方法，选择其中的最优方案。

具体来说我们应该定义一个数组dp[i,j]用来表示合并方法，i表示从编号为i的石头开始合并，j表示所求区间的结尾，sum表示的是石头的数量。

 

对于上面的例子来说，

　　 第一阶段：dp[1][1],dp[2][2],dp[3][3],dp[4][4] 因为一开始还没有合并，所以这些值应该全部为0。

 　　 第二阶段：两两合并过程如下，其中sum(i,j)表示石头的数量，即从i开始数j个数的和

 

              dp[1,2]=dp[1,1]+dp[2,2]+sum[1,2];

　　　　　dp[2,3]=dp[2,2]+dp[3,3]+sum[2,3];

　　　　　dp[3,4]=dp[3,3]+dp[4,4]+sum[4,4];

 

 

 

    第三阶段：三三合并可以拆成两两合并，拆分方法有两种，前两个为一组或后两个为一组

 

         dp[1,3]=dp[1,2]+dp[3,3]+sum[1,3]或dp[1,3]=dp[1,1]+dp[2,3]+sum[1,3];取其最优

　　　 dp[2,4]=dp[2,2]+dp[3,4]+sun[2,4]或dp[2,4]=dp[2,3]+dp[3,3]+sum[2,4];取其最优

    第四阶段：四四合并的拆分方法用三种，同理求出三种分法的得分，取其最优即可。以后第五阶段、第六阶段依次类推，最后在第六阶段中找出最优答案即可。

　  动态方程为dp[i][j]=dp[i][k]+dp[k+1][j]+sum[i][j];

　参考代码。

 

 1 #include <iostream>

 2 #include <cstdio>

 3 #include <cstring>

 4 

 5 using namespace std;

 6 

 7 //#define MAX 999999

 8 

 9 int main ()

10 {

11     int dp[210][210],sum[210][210],a[210];

12     int n;

13     while(~scanf("%d",&n))

14     {

15         //memset(dp,MAX,sizeof(dp));

16         for (int i=1; i<=n; i++)

17             scanf("%d",&a[i]);

18         for (int i=1; i<=n; i++)

19         {

20             dp[i][i]=0;//初始化为0

21             sum[i][i]=a[i];//将每堆石子的个数赋值进来

22         }

23         for (int len=1; len<n; len++)//按长度从小到大枚举

24         {

25             for (int i=1; i<=n&&i+len<=n; i++)//i表示开始位置

26             {

27                 int j=len+i;                    //j表示长度为len的一段区间的结束位置

28                 for (int k=i; k<j; k++)         //用k来表示分割区间

29                 {

30                     sum[i][j]=sum[i][k]+sum[k+1][j];

31                     if (dp[i][j]<dp[i][k]+dp[k+1][j]+sum[i][j])

32                         dp[i][j]=dp[i][k]+dp[k+1][j]+sum[i][j];

33                     //cout<<i<<" "<<j<<" "<<sum[i][j]<<" "<<k<<" "<<dp[i][j]<<endl;

34                 }

35             }

36         }

37         cout<<dp[1][n]<<endl;

38     }

39     return 0;

40 }

 http://acm.nyist.net/JudgeOnline/problem.php?pid=737

这是一道类似的题目，和上述代码有点区别，把7,15,31行修改一下即可哦~