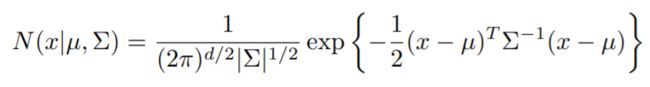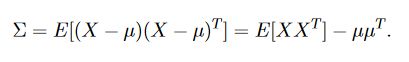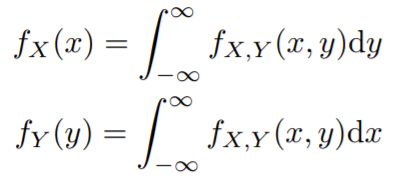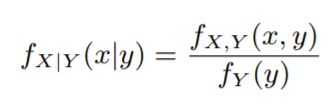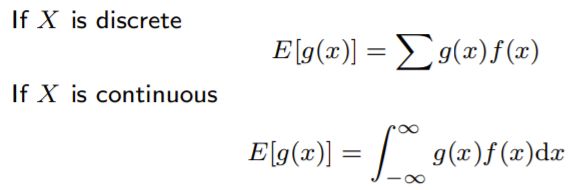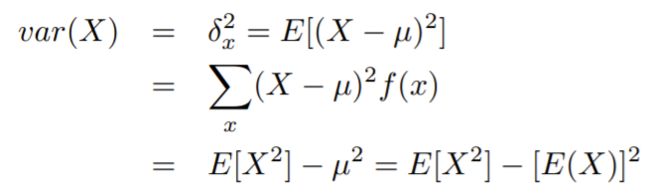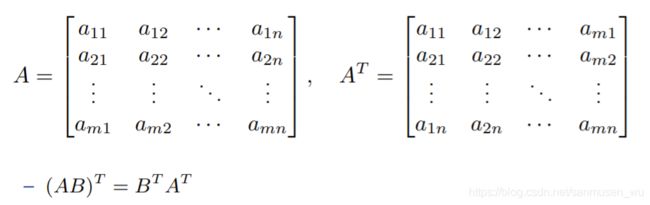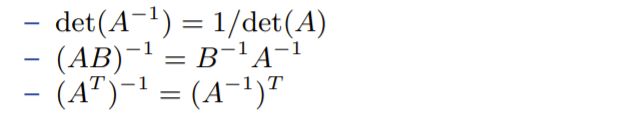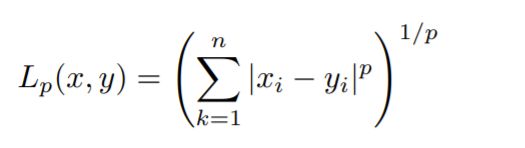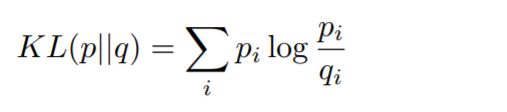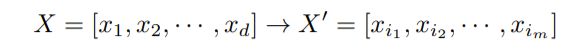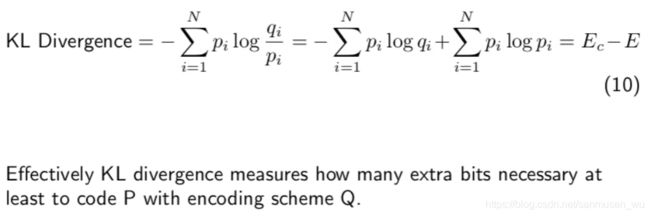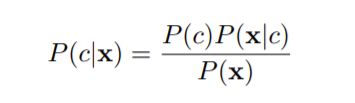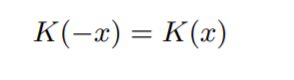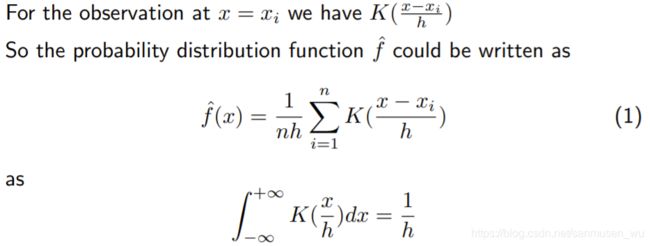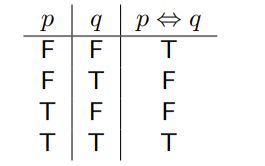INT104人工智能笔记
本文只梳理Lecture的知识点概念,不含Lab的代码实现
文章目录
- Lec1 什么是人工智能
-
- 什么是AI
- 当下AI
- 图灵测试Turing test
- 人工智能的困难
- Lec2 Python
- Lec3 概率空间与线性代数
-
- 概率空间Probability Space
- 随机变量Random Variables
- 概率密度/分布函数 Density/Distribution Functions
-
- 概率质量函数 Probability Mass Function (PMF)
- 概率密度函数 Probability Density Function (PDF)
- 累计分布函数Cumulative Distribution Function(CDF)
- 联合/条件概率 Joint/Conditional Probability Functions
-
- 联合概率函数Joint Probability Functions
-
- 偏积分求单个变量的密度函数
- 条件密度函数 Conditional Density Function
-
- 贝叶斯规则Bayes' rule
- 条件分布函数 Conditional Distribution Function
- 期望Expected Value
- 方差和标准差Variance & Standard Deviation
- 线性代数 Linear Algebra
-
- 向量Vectors
- 矩阵
- 行列式 Determinant
- 逆矩阵Matrix Inverse
- 距离 Distance
-
- 闵可夫斯基距离 Minkowski Distance
- KL发散 KL Divergence
- Lec4 优化
-
- 数学优化问题Mathematical Optimization
-
- 最小二乘拟合 Least-squares fitting
- 中心点 Weber point
- 凸优化问题 Convex optimization problems
-
- 定义
- 凸函数 Convex functions
-
- 凹凸性检验 Testing for convexity
- 利用子集性质对凸优化问题再一次定义
- 解决凸优化问题
- 得到优化的条件
-
- 如何得到使梯度为0的点
- 强大的第三方库
- Lec5 机器学习
-
- 模式Pattern/Category
- 特征Attributes/features
-
- 特征向量feature vector
- 特征空间feature space
- 散点图scatter plot
- 选取合适的特征
- 特征维度feature dimension
- 分类Classification
- 学习系统组成 Components of Learning System
- 过拟合和欠拟合 overfitting and underfitting
-
- 过拟合overfitting
- 欠拟合underfitting
- 机器学习步骤
- 机器学习的三个类别
- Lec6 数据缩减和特征选择
-
- 特征和模式Features and Patterns
-
- 选择适合的特征
- 维度灾难The Curse of Size and Dimensionality
- Peaking Phenomena峰值现象
- 数据处理
-
- 数据规约 Data reduction
-
- regression回归
- sufficient statistics充分统计
- histograms直方图
- clustering聚类
- sampling抽样
- 数据降维 Dimensionality Reduction
- 特征提取 Feature Extraction
- 特征选择 Feature Selection
-
- 单变量筛选特征-过滤器Filter
- 信息Information
-
- 信息内容Information Content
- 信息测量Information Measurement
- 信息熵Information Entropy
- 条件熵Conditional entroy
- 信息增益Information Gain
- 增益比例Gain ratio
- 多变量筛选特征
- Lec7 分类
-
- 分类Classification
- 评估分类模型 Evaluating Classification
-
- 混淆矩阵 Confusion Matrix
-
- F-Measure
- 复杂度 Complexity
- 稳健性 Robustness
- Receiver Operation Characteristics问题 (ROC)
-
- Area under Curve (AUC)
- 交叉验证 Cross Validation
-
- X验证中的数据划分 Data Partitioning Methods for X-Validation
- k折交叉测试集进行验证 k-fold Cross Validation
- 三分数据:
-
- 训练集Training set
- 验证集Validation set
- 测试集Test set
- Lec8判别函数
-
- 线性分割 Linearly Separable
-
- 线性判别函数Linear Discriminant Functions (LDF)
- 多分类问题Multiple-class Problem
- 如何确定每个类的判别函数
- 神经网络Neural Network
- 特征提取feature extractor
-
- 线性判别分析LDA(Linear Discriminant Analysis)
- 主成成分分析PCA(Principle Component Analysis)
- 独立成分分析ICA(Independent Component Correlation Algorithm)
- 非负矩阵分割NMF(Non-negative matrix factorization)
- Appendix附录
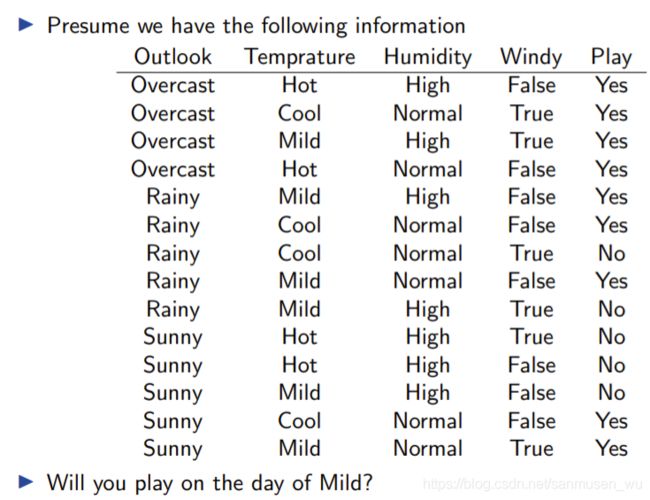
- Lec9 朴素贝叶斯
-
- 引子:
- 贝叶斯规则 Bayes’ Rule
- 模型拟然度 P(x|c)
- 朴素和对数拟然 Naive and Log-likelihood
-
- Occam剃刀 - Occam's Razor
- 贝叶斯估计和拉普拉斯校正Bayesian Estimation & Laplacian Correction
- 朴素贝叶斯分类器
-
- 朴素
- 分类器
- 例子
-
- 半朴素分类器 Semi-Naive Bayes Classifier
- 贝叶斯网络 Bayesian Network
- Lec10 聚类
-
- 无监督学习Unsupervised Learning
- 聚类Clustering:
-
- 层次聚类Hierarchical/Agglomerative Clustering
-
- 例子
- k均值聚类 k-means/Divisive Clustering
-
- 例子
- 高斯混合模型 Gaussian Mixture Model (GMM)
-
- 最大期望算法EM
- 评价GMM
- Lec11 非参数模型
-
- 非参数模型Non-parametric Modelling
- k-NN邻近算法(k-nearest neighbors algorithm k-NN)
-
- 样题
- Parzen窗(Parzen Window)核密度估计(Kernel Density Estimation)
-
- 核 Kernel
- 带宽Bandwidth
- 使用核密度解决分类问题
- 比较k近邻和核密度
- Lec12命题逻辑与Prolog
-
- 什么是逻辑Logic
-
- 命题Propositional
- 连结命题公式
-
- AND
- OR
- NOT
- IMPLIES (IF ... THEN ...)
- IFF( if and only if)
- 复杂连结命题公式
- 特殊命题公式
- 命题公式的局限
-
- 一阶逻辑FOL (First-Order Logic:Syntax)
-
- 术语Terms
- 谓语Predicates
- 量词Quantifiers
- 注意点
- 可判定性Decidability
- Prolog语言
Lec1 什么是人工智能
第一周主要是课程介绍,讲的很宽泛,略写了
什么是AI
- AI is the study of complex information processing problems that often have their roots in some aspect of biological information processing. The goal of the subject is to identify solvable and interesting information processing problems, and solve them. (David Marr)
- The intelligent connection of perception to action (Rodney Brooks)
- Actions that are indistinguishable from a human’s (Alan Turing)
当下AI
· 广泛成为学习生活中的工具-(神经网络,隐藏马尔可夫模型,贝叶斯网络,启发式搜索)
· 以模型,概率,统计,优化,算法为基础的交叉学科
1.聊天机器人2. 语音识别3. 机器翻译4. 问答系统5. AI游戏6. 网页搜索结果优化7. 新闻分类8. 广告推送9. 导航Navigation10. 搜索结果过滤11. 图像识别-(文字,人脸,肢体)12. 智能机器人13. 无人驾驶等
图灵测试Turing test
人工智能的困难
- 大数据集2. 最优化3. 噪点与缺失数据4. NP hard5. 描述问题(范化Paradigm)6. 寻找健壮的算法
Lec2 Python
Python基础语法
太基础的就不写了
隔位置切片
隔位置切片是数之后的第几个然后取,如例子是每两个取第二个,而不是隔2个取一个。
testlist=[0,1,2,3,4,5,6,7]
print(testlist[0:-1:2])
#------out------
[0, 2, 4, 6]
zip()
zip()将可迭代对象组成元组Tuple
key=[0,1,2]
val1=['a','b','c']
val2=['A','B','C']
print(list(zip(key,val1,val2)))
#------out------
[(0, 'a', 'A'), (1, 'b', 'B'), (2, 'c', 'C')]
列表解析式
testtuple=[(0, 'a', 'A'), (1, 'b', 'B'), (2, 'c', 'C')]
print([ch1+ch2 for (num,ch1,ch2) in testtuple])
#------out------
['aA', 'bB', 'cC']
迭代器
两个方法,__iter__()实现迭代器对象,__next__()将返回下一个迭代对象。
含有yield关键词的函数被称为生成器(generator),每次函数执行到yield的时候都会保存信息然后返回yield的值,下次调用next时从上次中断处继续运行。
def f(n):
yield n
yield n+1
yield n+2
item=f(5)
print(item.__next__())#next一次
print(next(item))#两次
print(item.__next__())#三次
print("sum after next 3 times:",sum(item))
newitem=f(5)
print("newitem sum:",sum(newitem))
#------out------
5
6
7
sum after next 3 times: 0
newitem sum: 18
Lec3 概率空间与线性代数
概率空间Probability Space
Ω: 样本空间 Sample Space
F: 样本空间内的一个非空子集,其内的元素被称为事件event
P: 概率测度 Probability Measure
P(Ω) = 1
随机变量Random Variables
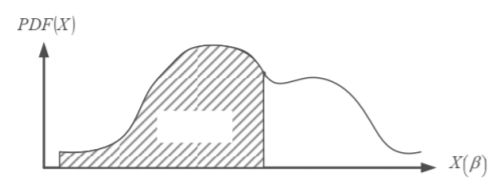
是一组函数(function)/映射(mapping),将可能的实验结果(人眼观测现象)映射到实数(real)或复数(complex)区间。
X : F → I, where F ⊂ Ω and I ⊂ R.
e.g. X(β) = r
例如,将一个人的身高映射到(0,3】(米)区间内,或者掷骰子将顶面映射到【1,6】内

概率密度/分布函数 Density/Distribution Functions
概率质量函数 Probability Mass Function (PMF)
表示离散随机变量在各特定取值上的概率。
1>单个位置的取值>0,各个取值的概率之和为1
概率密度函数 Probability Density Function (PDF)
概率密度函数是对连续随机变量定义的,本身不是概率,只有对连续随机变量的概率密度函数在某区间内进行积分后才是概率。
单独一位置取值>0,对全定义域的积分为1
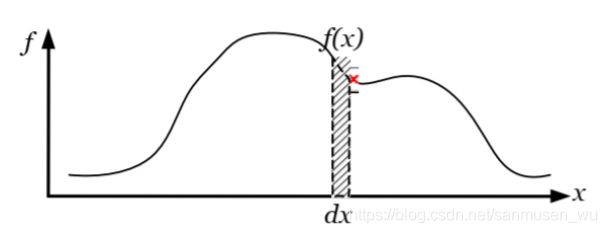
累计分布函数Cumulative Distribution Function(CDF)
变量可连续可离散
可以被定义为PDF的区间积分(integration)
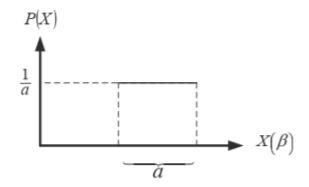
CDF(x) :FX(x) = P(X ≤ x)
- 均匀密度(Uniform density)
联合/条件概率 Joint/Conditional Probability Functions
联合概率函数Joint Probability Functions
对于独立事件,联合概率函数可表示为:
fX,Y (x, y) = fX(x) * fY (y)
偏积分求单个变量的密度函数
条件密度函数 Conditional Density Function
贝叶斯规则Bayes’ rule
已知 x发生的前提下y发生的概率 和 x单独发生的概率 ,可以用贝叶斯规则实现求y发生的前提下x发生的概率。

y:轻症
x:治愈
- P(x|y)表示后验概率,既希望求得的概率
(例如,我们希望求一位轻症病人A,他的治愈几率,由于A现在还未痊愈,所以没法得知A最后究竟多大可能治愈,这时就可以用贝叶斯估计) - P(x)表示先验概率,既观测到y之前客观的对x的全局概率,
(例如:病的治愈率为90%,是指统计的以前所有患者中有90%被治愈,而不是由刚刚才得病的A的数据得出来的) - P(y|x)表示假定x成立时,y发生的概率,
(例如:已治愈患者中轻症的比例) - P(y)表示证据,指新的未被计算进先验概率的证据,由于是已观测到的证据,所以一般已知。
(例如,A已经得了轻症) - P(y|x)/P(y)表示y对P(x)的影响。
(例如:已治愈患者中轻症比例 / A得了轻症,这个值越高,代表轻症对治愈的成功率影响越大。)
条件分布函数 Conditional Distribution Function
条件概率:y发生的前提下x发生的概率,对应CDF
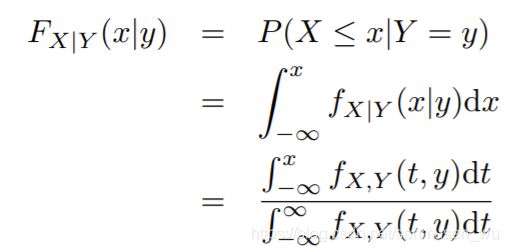
对于独立事件的条件分布函数:
fX|Y(x|y)=fX(x)
期望Expected Value
- E[aX+b]=aE[X]+b
- 独立事件:E[XY]=E[X]E[Y]
方差和标准差Variance & Standard Deviation
线性代数 Linear Algebra
向量Vectors
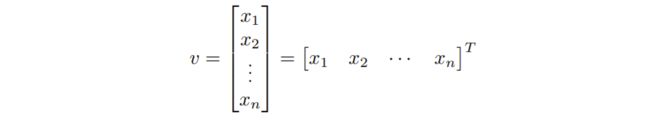
单位向量unit vector:
![]()
点乘 Inner product:

叉乘 Geometrically-based:
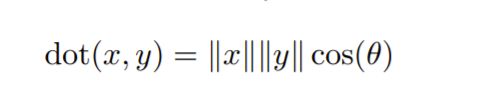
正交 Orthonormal Vectors:
向量x1,x2,…xn是否正交的判断:

· 向量空间 Vector Space:
F:实数
W:向量
对于所有λ ∈ F and u, v ∈ W,向量空间可以表示为: λu + v ∈ W
· 向量组合 linear combination:
顾名思义,向量v1,v2,…vn组合在一起
scalars:标量/参数/权值

· 向量集S张成(span)空间W:
W内的所有向量可以由S内向量组合而成,这个关系叫做S张成空间W。
· 线性无关 Linear Independence:
v1,v2,…vk线性无关 当且仅当 不存在非0标量能够使之向量组合为0
换言之,没有两向量处于同一条线上。

· 基 Basis:
S = (v1,v2,…vk) is a basis for a vector space W if:
- vj互相线性无关
- S可以张成W
注意:基内向量不一定两两正交
矩阵
行列式 Determinant
det(AB)=det(A)det(B)
· 特征向量和特征值 Eigenvectors and Eigenvalues:
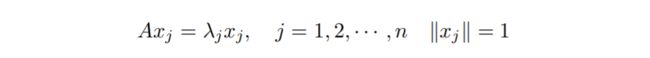
· 特征方程 Characteristic equation:
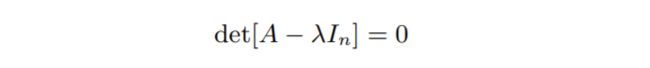
· 行列式和特征值 Determinant & Eigen values:
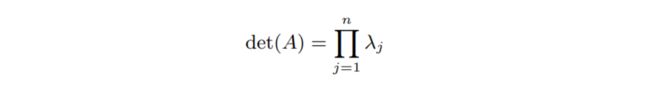
逆矩阵Matrix Inverse
乘起来是单位矩阵的两个方阵

奇异方阵 singular:逆不存在
病态 ill-conditioned:指任何小的扰动会使解产生较大的变化
(举个例子,斜率为0.0001的斜线与y=1的交点为x=10’000,当斜率发生微小改变成了0.0002,与y=1的交点变成了x=5‘000,变化了5000)
距离 Distance
欧氏距离是点的空间距离
非欧式距离是点的属性差别
通常用一个对称的矩阵表示i和j之间的距离(类似于邻接矩阵)
映射距离度量d的4要素:
- d(x, y) > 0.
- d(x, y) = 0 iff x = y.
- d(x, y) = d(y, x).
- d(x, y) < d(x, z) + d(z, y) (triangle inequality )
实际应用到聚类问题,不需要考虑对称性和三角不等式
闵可夫斯基距离 Minkowski Distance
-
当p=1时,就是曼哈顿距离 Manhattan Distance
既各个维度方向上的差异之和
x2-x1+y2-y1 -
当p=2时,就是欧氏距离 Euclidean Distance
两点之间的连线的长度
勾股定理 -
当p→∞时,就是切比雪夫距离 Chebyshev distance
所有维度的差异中,选择差异最大的那一个维度上的差异
max(x2-x1,y2-y1)
KL发散 KL Divergence
p为真实分布,我们预估一个近似的分布q
KL发散既是形容q(x)被用于近似p(x)时的信息损失,用来衡量俩概率分布间差异大小
KL散度越大,表达效果越差
机器学习的目标既是找出参数θ使模型与样本间的KL散度尽可能小。
因为其非对称且不满足三角不等式的性质
其作用主要不是用来度量距离,但是学校PPT讲也可以在度量距离时使用。
Lec4 优化
数学优化问题Mathematical Optimization
PPT解释:
给定目标函数f(x),和限制函数g(x),找出合理的x,使目标函数f(x)最小。
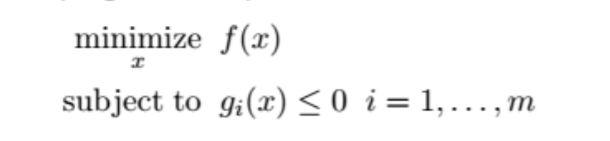
其中,
- x是优化问题中的优化变量-optimization variable,既是参数,也就是吴恩达的教程里的θ
- f(x): 目标函数-objective function-既学习结果的准确度
- gi(x): 限制函数-constraint function-既根据先验知识对参数x做出的限制
· 何为最优(optimal solution):
如果对于所有符合以下条件的x:
![]()
存在一个xp使 所有f(x) ≥ f(xp) ,则称xp为最优解。
易混淆单词:
Mathematical program / mathematical optimization problem / optimization problem:形容数学优化问题本身
Numerical optimization / mathematical optimization / optimization:形容对以上问题的研究既解决方法
最小二乘拟合 Least-squares fitting
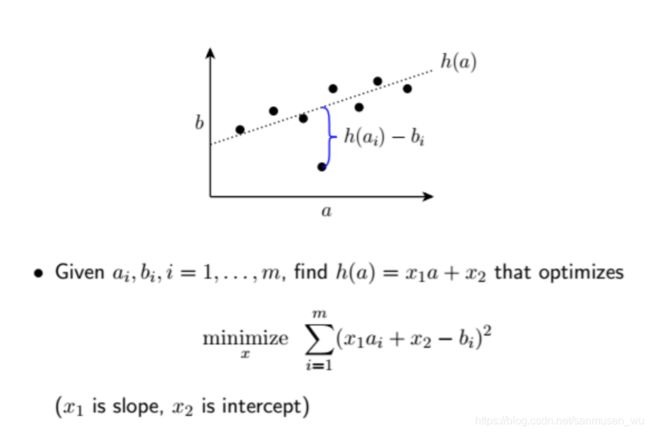
给定数据集a,b,找到能够拟合这些点的直线h(a)=x1a+x2(x1为斜率slope,x2为截距intercept),使之到各点的纵向距离之和最小
该问题没有限制函数
中心点 Weber point
![]()
给定数据集(ai,bi),找到一中心点,使之到各点距离之和最小
该问题可以设置限制函数(subject to…), 约束中心点在所有点的坐标范围内

凸优化问题 Convex optimization problems
定义

f表示一个凸函数映射,x被限制在凸集C内(convex set),凸集C可以概括为许多凸函数的集合。
目标函数为凸,限制函数为凸,则我们可以找出最优解,同时也是全局最优解。
· 什么是凸集(convex set):
对于任意参数θ∈[0,1], 任意x1,x2∈C,存在 θx1 + (1-θ)x2 ∈ C, 则称C为凸集。
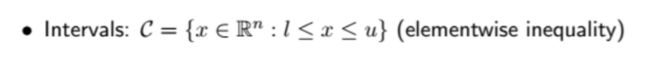
![]()
![]()
· 凸集的交集:

i=1,2,…,m,写的很像求和,交集符号原来还能这么用的吗。。。
凸函数 Convex functions
f(θx1+(1-θ)x2) ≤ θf(x1) + (1-θ)f(x2)
凸函数上任意两点的连线与函数没有交点
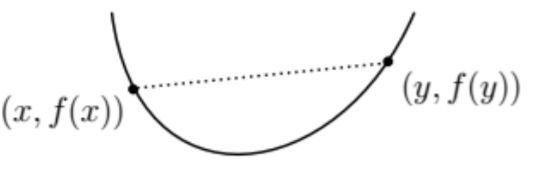
· 凹函数concave:
如果 -f 是凸函数convex,那么 f 就是凹函数concave
如果又凸又凹,称为仿射函数(affine function),就是直线

凹凸性检验 Testing for convexity
· 凸函数处处凸
· 对于数量输入f:R→R,f的二阶导不存在负值。
· 对于向量输入,▽x2f(x)≥0,▽x2f(x)为黑塞矩阵
· 什么是黑塞矩阵Hessian Matrix:
在工程实际问题的优化设计中,所列的目标函数往往很复杂,为了使问题简化,常常将目标函数在某点邻域展开成泰勒多项式来逼近原函数,此时函数在某点泰勒展开式的矩阵形式中会涉及到黑塞矩阵----它是一个多元函数的二阶偏导数构成的方阵,描述了函数的局部曲率。

一堆凸函数例子:

利用子集性质对凸优化问题再一次定义

其中,f()是凸函数,g(不等式约束)是凸函数,h(等式约束)。就是把凸函数一开始的定义展开了。
由此定义的凸优化问题的所有局部解都是全局解
相关性质:
- 定义:对于可行解(feasible)x,如果不存在另一个可行解y且 f(y) < f(x),则x是全局最优global optimal
- 定义:对于可行解x,如果存在一个数R>0,使得对于所有可行解y,满足||x-y||2≤R,f(x)≤f(y), 则称x为局部最优locally optimal
(这里的下标2表示按照欧式距离(闵可夫斯基距离中,p=2)算模,也就是两点之间的直线距离) - 定理:对于凸优化问题,局部最优点既是全局最优。
一堆凸函数优化的例子:
- least-squares
- weber point
- linear programming
- quadratic programming
- nonconvex problems
- Integer programming
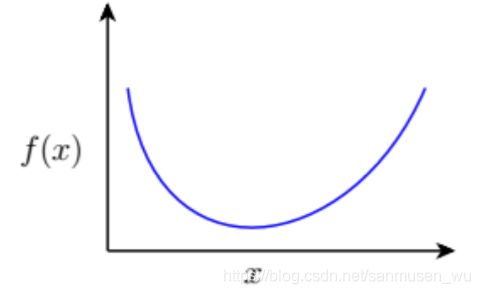
解决凸优化问题
对于二维曲线而言,关注切线的斜率,切线斜率为0的点将会是最小点
得到优化的条件
对于f:Rn→R的多维函数,f在最优处的梯度为0,对于不受限制(unconstrained)的凸优化问题,解只有一个
· 什么是梯度gradient:
包含各维度的斜率的向量
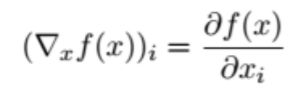
如何得到使梯度为0的点
- 直接用导函数计算-Direct solution
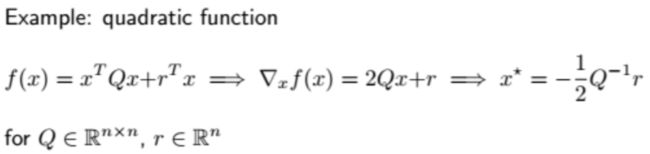
- 梯度下降-Gradient descent
按照当前斜率方向走小步
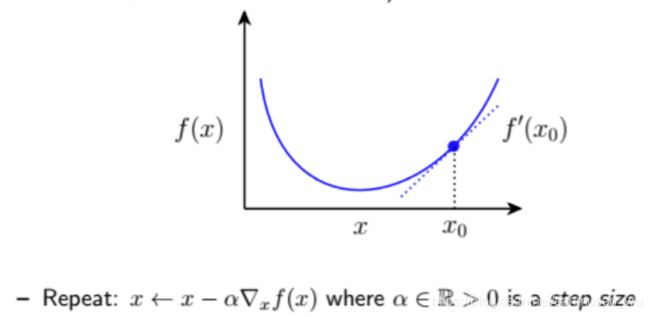
- 牛顿迭代法Newton’s method
依旧依靠梯度,下一步会在 f(x) / f’(x)处
f(x)的精确解是函数的零点

- 障碍法 Barrier method
(原目标函数是 minimize f(x) ,而且对x有一个不等式约束条件)
通过在f(x)中添加惩罚函数(如-tlog(-g(x)),去掉不等式约束条件g(x)并在目标函数中模拟原约束(越靠近约束点惩罚函数越大),使用牛顿迭代法求解目标函数最优值。
其中+/-log(i)函数靠近y轴时值接近正/负无穷,进而提供了一个“边界”,也就是远离的趋势,t越大代表趋势越强烈。
强大的第三方库
实际使用代码解决最优化问题时,可以直接调用已有的第三方库。
Lec5 机器学习
· 什么是机器学习:
机器学习可以从作用上划分为分类Classification,和解决各种各样的问题Problem Solving,帮助人类生产生活。
· 为什么机器学习:
通过使用足够多的样本进行训练,模型所总结出的规律能够适应其他那些未被观测的个体。也就是说,通过足够多的训练集拟合出的目标函数(target function)能够尽可能与全集的目标函数相同。
模式Pattern/Category
是一种个体,可以被贴上‘名字’或’标签’以表示其某种意义
(例如书,笔,纸,他们有名字并且唯一指代了一种物品)
模式与混乱chaos相反,混乱chaos无法具有意义,在图片上指噪点,在音乐里面指噪声。
特征Attributes/features
既是属性特点,在同种个体间共有的东西。
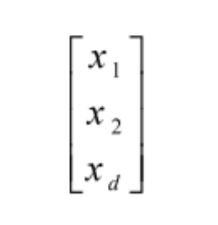
(例如书,笔,纸,都有长度,颜色,材质。这些属性既是特征,在对个体进行学习时,将同种或不同种的特征组合在一起形成特征向量,如笔的特征向量可以是[10cm,0.8cm,黑色,塑料]T)
特征向量feature vector
特征空间feature space
特征向量所处的空间
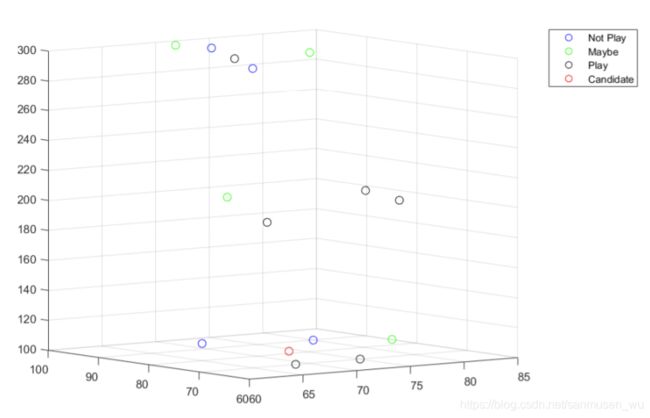
散点图scatter plot
个体以点的形式(向量形式)在特征空间中表示,这种表示为散点图
选取合适的特征
特征的选取应当能够按照目标区分某一类。
(例如,对书籍进行题材分类,一般会按照书里的某一单词出现次数进行分类,而不会通过书的封面颜色区分)
选取好的特征能够使分类效率更高,更准确,表现差的特征会导致界限模糊或无法区分。
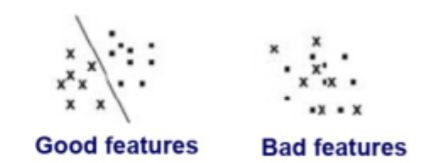
特征维度feature dimension
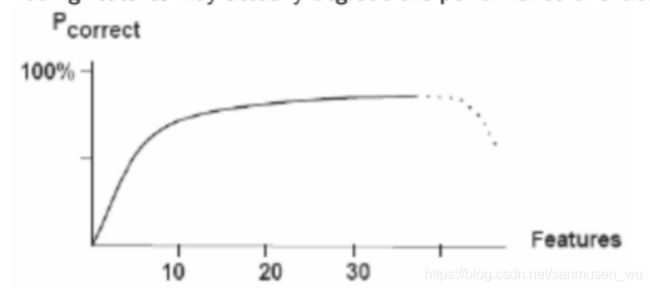
维数灾难 curse of dimensionality:
当特征的维度增加,为了维持样本在特征空间内的密度,往往需要更多的样本。换句话来说,就是选取的特征越多,训练集数量也要越多,否则会造成学习不充分,也就是欠拟合。
分类Classification
Assign object/event to one of a given finite set of categories.
按照一定的策略将对象分成若干子类
· 如何评估分类算法:
准确度(使用测试集评估);
训练时间(关注算法的学习速率rate/speed);
测试时间(关注算法学习结果,也就是算法的分类速率rate/speed)
学习系统组成 Components of Learning System
- 传感器和预处理 Sensors and preprocessing
- 特征选择 Feature extraction
- 训练 Training
- 学习算法 Learning algorithm
- 分类器 Classifier
过拟合和欠拟合 overfitting and underfitting
过拟合和欠拟合对训练集表现良好,而在实际应用(测试集,验证集)中会出问题。
过拟合overfitting
既是指由于机器学习的过于充分,过于依赖训练集展现的信息,从而约束了有效认知。
例如将一群青少年的照片作为训练集,训练人脸识别。因为训练的过于充分,导致机器认为只有长的比较年轻的才是人脸,而在实际应用中没法识别小孩和老人。
欠拟合underfitting
欠拟合指机器学习的不够多,从而扩大了有效认知。
例如将一群人脸作为训练集,人脸识别。因为训练的次数不够多,或者人脸数量太少,导致机器认为只要有五官的都是人脸,然后实际应用识别出狗脸是人脸。
无论是过拟合还是欠拟合,都会使机器学习出来的模型不太靠谱↓
机器学习步骤
机器学习的三个类别
根据学习方法划分的:
· 监督学习supervised learning
···· 训练集包含标签label,算法依赖于个体的特征值和标签进行识别并训练。
· 非监督学习unsupervised learning
···· 训练集无标签,算法自己分析训练集的分布或构成,进行训练。
· 强化学习reinforcement learning
···· 通过不同的输入和奖惩制度进行训练。
Lec6 数据缩减和特征选择
特征和模式Features and Patterns
选择适合的特征
- representative:代表一个个体
- characteristic:不同类的个体的特征值之间类似
- interpertable:可解释为人类使用的特征
- suitable:从获得数据中的自然选择
- independent:特征之间不需要关联(如:物体的三维长度和物体的体积表达同一个意思)
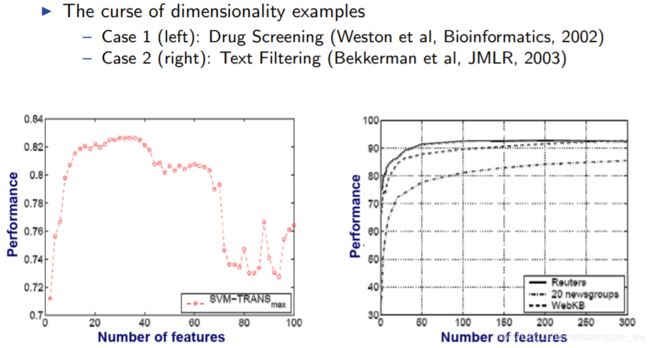
维度灾难The Curse of Size and Dimensionality
—The probability of misclassification of a decision rule does not
increase beyond a certain dimension for the feature space as the
number of features increases.
—This is true as long as the class-conditional densities are completely
known.
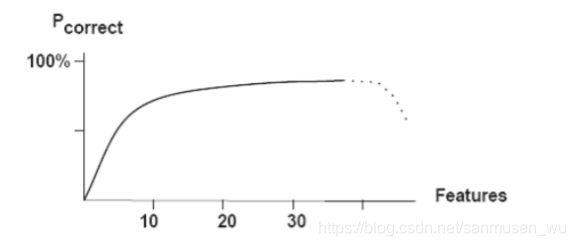
Peaking Phenomena峰值现象
数据处理
300x300清晰度图片有90’000个像素,而900x900图片则有达810’000像素,再考虑算法复杂度十分恐怖。
数据规约 Data reduction
目的:减少数据量,但是又能尽可能表示出原有数据所表现的特征。
方法:
regression回归
数据建模确定模型
sufficient statistics充分统计
保持原始总体统计信息(statistical information),建立函数
histograms直方图
将数据分为不同的桶buckets,存储这些桶的平均值
划分规则:等宽,等频,等方差
clustering聚类
使用相似性方法对数据聚类,只存储聚类表示
sampling抽样
使用部分数据表示整体(舍弃部分个体)
采样策略:
· 简单随机抽样Simple Random Sampling
···· 抽取每个个体的概率相同
· 不放回抽样Sampling without replacement
···· 选取个体后,不放回总体
· 放回抽样Sampling with replacement
···· 选取个体后,将其放回总体,之后还会考虑抽取该个体
· 分层抽样Stratified sampling
···· 将总集分为近似的子集,根据子集大小,选取子集中的部分个体

数据降维 Dimensionality Reduction
什么是数据降维:减少所考虑的特征数量(’长宽高‘和‘体积’等同,二者择一即可)

特征提取 Feature Extraction
什么是特征提取:通过结合两个以上特征组合出新特征,原来的俩特征就被结合了,同样减少了维数(’一条直线的x轴方向上一个单位间的y轴变化‘以及’一条直线的y轴方向上一个单位间的x轴变化‘ 其实可以变成一个特征----斜率)
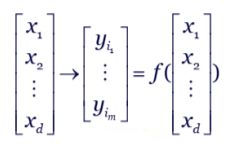
特征选择 Feature Selection
- 单变量法Univariate method
一次选择考虑一个特征 - 多变量法Multivariate method
一次选择考虑一个特征子集
另一类方法:
- 过滤器Filter
独立于分类器,对特征子集( features subsets)进行rank - 包装Wrapper
使用分类器评估特征子集(比较不同特征子集选择下的学习结果) - 嵌入Embedded
在分类的过程中改变每个特征的权重(把特征权重写进代价函数),这样学习的过程中特征权重就会自己调整
单变量筛选特征-过滤器Filter
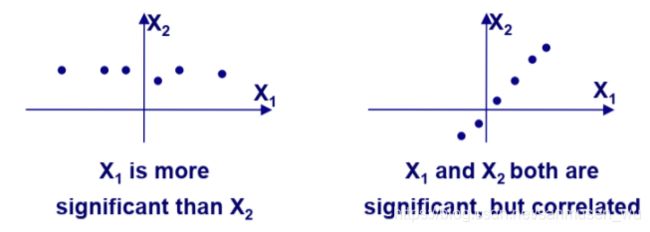
评估所选特征子集Criteria=Significant difference * Independence
· Significant difference显著差异:通过某一特征更好的差分训练集
· Independence独立性:特征间保持无关(反例:同时选取长宽高和体积)
信息Information
信息内容Information Content
信息测量Information Measurement
不确定性函数:
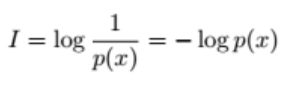
x概率越高,该事件的x部分(sample) 确定性越强,不确定性越弱,不确定性函数越小。
(例如,明天下雨的概率是99%,则明天的天气不确定性很小,几乎可以确定就是下雨,-log(0.99)→ 0)
信息熵Information Entropy
事件的熵E( C )或H(X),单位是bit/average
X是事件整体
x是部分事件
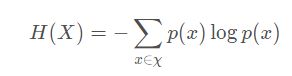
形容一个事件整体的不确定性,其为事件每部分的不确定函数根据其发生概率加权和。
(例如,明天天气怎样的不确定性=晴天概率x晴天不确定性+下雨概率x下雨不确定性+…)
当每部分的不确定性相近,代表事件整体非常不确定。
条件熵Conditional entroy
X为事件整体,Y为条件整体:
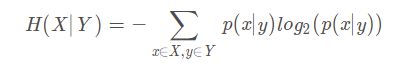
形容一个已知前提条件Y后事件X的不确定性,对于每部分前提y,关于事件每部分x在y发生的前提下的不确定函数加权相应的事件每部分x在y发生的前提下的发生概率之和。
信息增益Information Gain
IG为信息增益,表示通过假设先发生条件A,减少了事件C的多少不确定性。
代表信息(前提)A的有用程度。
![]()
增益比例Gain ratio
Information gain measure is biased towards attributes with a large
number of unique values
信息增益对于独特值数量量非常多的事件很有利,因此使用比例消除这种优势。
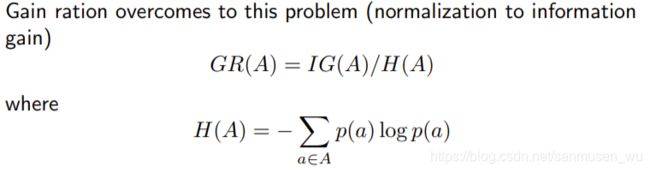
多变量筛选特征
· Complete/exhaustive
检查特征子集的所有组合
可以找到最优
· Heuristic
通过经验选择子集
使用增量生成子集 incremental generation
可能遗漏最优
· Random
随机选取特征
最优取决于选择次数
需要更多用户定义的输入,决定了结果的最优
Lec7 分类
分类Classification
这周主要讲二分类binary classification

利用训练集(特征值和label)训练模型,然后用这些模型去分类新的个体(只有特征值)

· 训练Training
依据训练集(training set)中的数据,训练集的数据被其标签明确分类,模型需要做的是学会按照这些给定数据确定分类标准
· 推论Inference
用于对未来的未知物体进行分类,在这之前需要估计模型的精度accuracy以评估模型:
评估模型好坏需要使用测试集test set,测试集需要独立于训练集,以测试模型对未探知的个体的分类精度。
Accuracy rate:correctly classified samples / test set
评估分类模型 Evaluating Classification
混淆矩阵 Confusion Matrix
True Positive (TP):模型判断为 +(正P),实际情况也是 +(判断正确True)
True Negative (TN):模型判断为 -(负N),实际情况也是 -(判断错误True)
False Positive (FP):模型判断为 +(正P),实际情况却是 -(判断错误False)
False Negative (FN):模型判断为 -(负N),实际情况却是 +(判断错误False)
利用TP,TN,FP,FN构建的算式,形容模型在某一方面的能力
将实际情况为正的集合称为n+,将实际情况为负的集合称为n-
- Recall(Sensitivity): 所有实际为正的个体中分类为正的比例
TP / (TP+FN) = TP/n+ - Fall-out:
FP / (TN+FP) = TP/n- - Miss rate
FN / (TP+FN) = FN/n+ - Specificity(Selectivity)
TN / (TN+FP) = TN/n-
- Precision,在所有被分类为正的个体中实际为正的比例
TP / (TP+FP) - Accuracy,模型正确分类的比例
(TN+TP) / (TP+TN+FP+FN)
F-Measure
将Precision和Recall加权调和平均:

β置为1时,式子即为F1-Measure(应该会出关于这些的计算题):
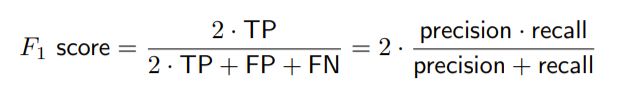
复杂度 Complexity
构建模型(训练模型 training time)的耗时
使用模型(用模型对新个体分类classification time)的耗时
稳健性 Robustness
处理噪声和缺失的数据的能力 handling noise and missing values
处理部分几个不正确的训练集数据的能力 handling incorrect training data
Receiver Operation Characteristics问题 (ROC)
给定以下预测值和标签,现有不同的阈值去区分1和0,如何评估这些阈值的好坏

Area under Curve (AUC)
交叉验证 Cross Validation
通过使用部分训练集作为交叉验证集,增强验证集表达整体数据的能力
可以用于模型评估,进而可以选择最好的学习模型(超参数选择)。
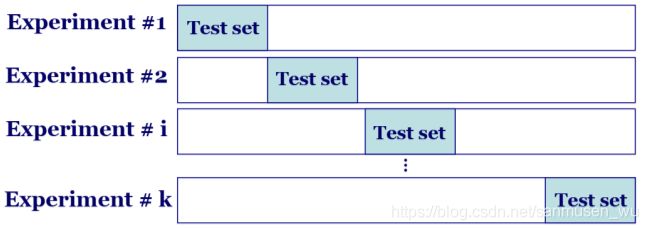
X验证中的数据划分 Data Partitioning Methods for X-Validation
- 随机抽样:假设数据是是均匀分布的(uniformly distributed),随机抽样得到训练集和测试集。

- 引导Bootstrap:使用n个初始数据替换部分训练集。部分数据可能在训练集中重复多次,可用于估计数据分布
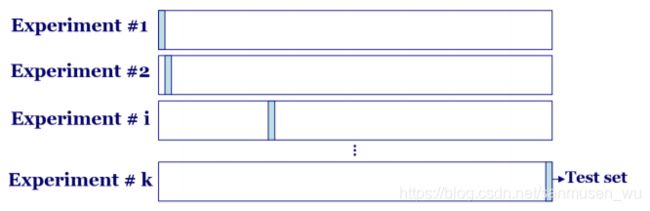
k折交叉测试集进行验证 k-fold Cross Validation
对模型的评估。
将数据划分为k个互斥且大小相等的子集,
进行k次训练和测试,每次选取第 i 个子集作为测试集(1≤i≤k),其余子集作为训练集。用k次测试的结果的平均数去评估的模型的performance。
该方法可以避免固定划分数据集的局限性、特殊性,这个优势在小规模数据集上更明显。
· 留一交叉验证 Leave-one-out Cross Validation:
k=数据样本的总数量n,n个数据划分成k个子集,每个子集只包含一个数据,每次只留下一个单个样本作为测试集,其余n-1个样本作为训练集。
三分数据:
将总数据互斥地三分:
训练集Training set
喂给模型进行学习,拟合分类器参数
验证集Validation set
属于学习过程中的一环,根据验证集结果从备选的几种训练模型中选择最好的。
测试集Test set
用于评估训练结束后分类器的表现,也就是模型的泛化能力(泛化能力较差就会过拟合/欠拟合)
· 为什么分成三个集:
训练集与验证集互斥:因为在训练过程中有选择表现较好的那一种模型的需要,所以使用验证集
测试集与(训练集,验证集)互斥:因为有评估模型在应用到实际生活中的正确率的需要,而且又因为模型完全学习于训练集,导致需要与训练集互斥;模型使用了测试集选择最优模型,无形中依赖于测试集降低了一点错误率,为了真实性,需要与验证集互斥
Lec8判别函数
线性分割 Linearly Separable
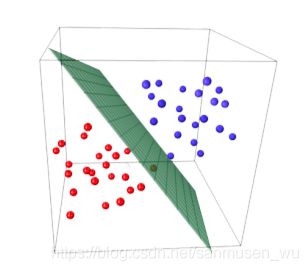
线性判别函数Linear Discriminant Functions (LDF)
![]()
w表示权重向量,x表示特征值,w0表示偏差(在二维直线中表现为截距)。
分类需要分成多个类,每个类都有自己的判别函数,可以认为判别函数的值代表“这个样本属于这个类的可能”
通过将每个新的个体的特征值带入各个类的判别函数计算,可推定新个体属于唯一判别函数结果>0的那个类。
下图的各个颜色的线既是各个类的判别函数取0的点的集合,也就是分界线(boundary)。
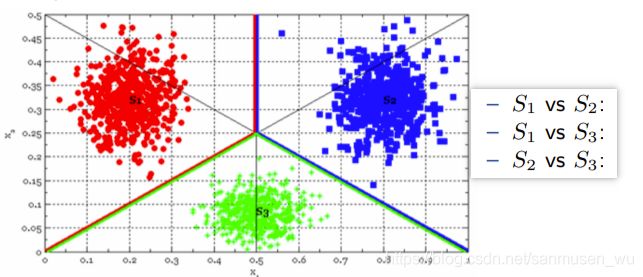
多分类问题Multiple-class Problem
如果只需分两类,显然极大可能用一条直线能分出两个区域,
→如何分成三类或者四类这种多分类文问题,可以继续使用线性判别函数吗
→可以,主要分为:
-
完全线性分离Completely linearly separation
如 (A | BC,B | AC,C | AB), one VS the rest
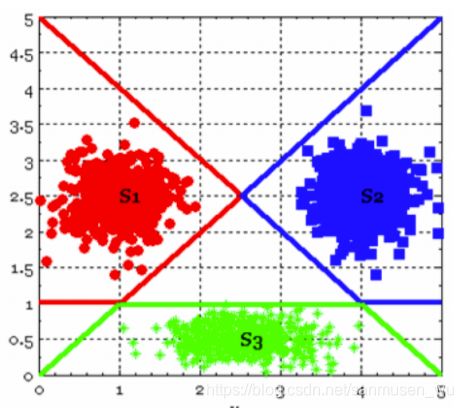
· 对于一个新的个体,关于所有类的判别函数,只在一类的判别函数g(x)>0,则属于那个类。计算题:
····若共三类,需证新个体属于1类,需证明以下两点
····g12(x)>0 :g1(x)- g2(x)>0
····g13(x)>0 :g1(x)- g3(x)>0
· 注意到在使用one VS the rest策略时,格子内有些部分没有被包含进任何块,如果新的个体位于这些部分(既全部g(x)<0,不属于任何颜色块),则称该区域为不确定区域。 -
MvM Method
MvM则是每次将若干类做为正例,若干其他类做为反例
如(ABC|DEF)
如何确定每个类的判别函数
神经网络Neural Network
判别函数可能不是线性的而是由多个函数相互组合形成的,以下神经网络结构的各个节点输出对前一层n个数据按照某种函数处理的结构。
相关名词:
感知器Perceptron:最左边的点,负责参数输入
神经元neuron:每个圆圈
层layer:参数处理传递的深度(左右)
激活函数activation function:负责将神经元的输入映射到输出端
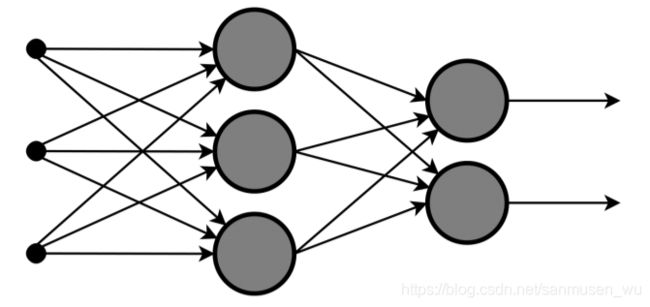
多层神经网络被认为是深度学习系统deep learning。
· The extension along space axis results Convolutional Neural Network
(with some simplification)
· The extension along time axis results Recurrent Neural Network
(with more controls between time slices)
特征提取feature extractor
前面提到了数据需要在特征空间内被分割成不同的类,
然而,可能由于特征选取不太恰当导致选取的特征间出现关联或者数据在特征空间中过于分散,特征维度过多导致训练速度忒慢。
因此,需要进行特征提取,从已有特征中提取某些有用的特征,使个体在特征空间内以较低维的方式分散开来,有利于计算机快速有效计算,加强算法可靠性。

线性判别分析LDA(Linear Discriminant Analysis)
属于监督学习,
将个体特征投影到低纬度直线上,尽可能差分不同类型的个体。
如下图,蓝色和黄色所投影到直线的区域之间可被明显区分

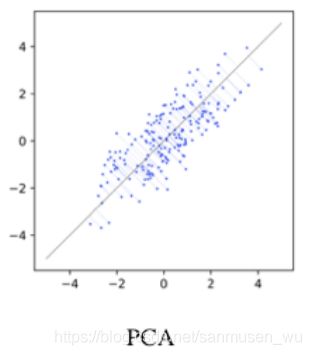
主成成分分析PCA(Principle Component Analysis)
无监督学习,
将个体特征投影到低纬度直线上,提取出重要特征(主成),尽可能差分每个个体。
什么是主成:对区分每个个体有最大作用的特征既是主要成分
独立成分分析ICA(Independent Component Correlation Algorithm)
为什么使用ICA:之前的方法都是人为规定(先验)一种显著的差异,而这种差异没法保证互相独立,以至于没法客观分析不同类之间的最好的区分方式。而且都要降维。
什么是ICA:PPT没怎么讲,可以理解为线性变换坐标系(?),不需要降维。

非负矩阵分割NMF(Non-negative matrix factorization)
把数据矩阵分解成系数矩阵W和权重矩阵H,试图找到一个权重矩阵(weight matrix),使系数矩阵(coefficient matrix)足够稀疏,这些分散开来的矩阵能够用于分类。

Appendix附录
· 最小均方差Least Mean Squared Error
之前讲到了使用梯度下降逼近代价函数(式子1)最小的点
这里直接对代价函数求导算出斜率为0的点(式子2)
然后处理2式等式得出模型的参数w(式子3)
· 误差平方和Sum of Squared Error
通过添加常数特征和一个参数吸收截距(式子1)
a既是参数,咱们的目标是拟合参数,组成函数g(x)(式子2)
将这些不符合的(g(x)<0的)训练集的特征变成负数(式子3)
再次拟合参数a,使得g(x)=b>0 (b一般是1)(式子4)

伪逆矩阵pseudoinverse matrix
一般来说只有方阵才有逆矩阵,这个方法能得出非方阵矩阵的一般化逆矩阵,如上图的aT

· Ho-Kashyap Method
上个方法的b是先验的,这个方法使用梯度下降寻找最合适的b


· Fisher Linear Discriminant Method
“ 用通俗的话来说就是针对 N 维空间中的某点 x=(x1,x2,x3,…,xp)寻找一个能使它降为一维数值的线性函数y(x),即把N维空间的数据投影到一条直线上,并应用它把 N 维空间中的已知类别总体以及求知类别归属的样本都变换为一维数据,再根据类间的亲疏程度(即设定一阈值)把未知归属的样本点判定其归属。既最大限度地缩小同类中各个样本点之间的差异,又最大限度地扩大不同类别中各个样本点之间的差异,即聚类的类间方差与类内方差之比达到极大(借用了一元方差分析的思想),这样才可能获得较高的判别效率。”
原文链接:https://blog.csdn.net/xiaqunfeng123/article/details/17266071

Lec9 朴素贝叶斯
w12的TTL有更多贝叶斯相关内容
朴素贝叶斯假设观测值x的特征间相互独立
引子:
当我们随机掷骰子60次时,按照概率分布各面的次数应完全相等:

但是实际情况可能是:

发现与预想的情况不一样。
相关名词:
- prior probability (or prior knowledge):先验概率,推测出来的较理想化结果,也叫做正向概率。(第一个表的6个10)
- posterior probability:后验概率,给定以往实验中得到的观察结果,反推某种事件发生的概率,也叫做逆向概率。(后面那个乱的表)
贝叶斯规则 Bayes’ Rule
- P(c|x):后验概率-posterior probability,贝叶斯公式希望求得的东西。
我的个人理解是个体概率。 - P( c): 先验概率- prior probability
(如果prior未知,则假定其等概率→c1=c2=c3…)
我的个人理解是群体概率。 - P(x|c): 拟然度- likelihood
- P(x): 观测事实,证据- evidence factor or observation
观测事实通常被认为是一个常数,或者有时候不参与计算
用处:可用于参数估计,分类和模型选择
Bayes’ Rule can be used for various purposes such as parameter estimation, classification and model selection.
给定数据集,对于不同类和样本,观测结果保持不变。
推导贝叶斯:联系条件概率公式可以看出其贝叶斯规则的分子部分既为P(c∩x),也就是:
c发生的前提下考虑x发生的概率=P(x|c)P(c) = P(c∩x) = P(c|x)P(x)=x发生的前提下考虑c发生的概率
模型拟然度 P(x|c)
什么是拟然度:拟然度表示观察结果x受到参数c(先验数据)的影响程度。
例如设定:
c→献过血
x→是O型血
求:
P(c|x)→如果一个路人甲是O型血,甲献过血的概率是多少
假设:
先验概率P©=0.4→约等于地球上有40%的人献过血,甲献血的先验概率0.4
拟然度 P(x|c)=0.9→献过血的人中有90%是O型血
显然,当拟然度够大时,甲献过血的概率也够大
我们知道献过血的人里面有90%是O型血,这影响了甲是O型血的前提下,ta献过血的概率,但注意这两者不完全等同。
机器学习可以根据给定的后验概率(模型预测值)和先验概率(label)计算模型的拟然度,再选择拟然度大的表现好的模型,使模型拟然最大的过程也被称为 最大拟然估计Maximum Likelihood Estimation (MLE).

朴素和对数拟然 Naive and Log-likelihood
当x内特征过多时,拟然结果会很恐怖,因为对x的拟然=对各个特征的拟然结果的乘积,这也涉及到了朴素的概念。
朴素贝叶斯假设观测值x的特征间相互独立
举个例子说明下特征之间相互独立的好处:
c→献血
x1→O型血
x2→男性
x3→学生
拟然 P(x1.x2,x3|c)=未知→献过血的人中有多少比例是O型血,而且是男性,还是个学生
如果x之间不独立,那么我们则需要在献过血的人中查找同时满足这三个条件的人的比例,由于数据的稀疏性,同时满足这么多条件的数据过少,结果产生较大偏差。
假设他们之间相互独立,那么只需要分别求P(x1|c) x P(x2|c) x P(x3|c)即可,把满足各个特征要求的人的条件概率相乘
但是,乘法计算也使得计算变得复杂

因此,取对数,使乘法运算变成log之间的加法运算
![]()
Occam剃刀 - Occam’s Razor
如无必要,勿增实体
the model favours the simplest (smallest) hypothesis consistent with the data
尽可能用简单高效的假设模型表示数据
”科学家应该使用最简单的手段达到他们的结论,并排除一切不能被认识到的事物“
贝叶斯估计和拉普拉斯校正Bayesian Estimation & Laplacian Correction
如果一种情况从未在历史中(训练集)出现过(比如献过血的人中没有一个人是O型血,而且是男性,还是个学生),使用贝叶斯去估就会出大问题,分子直接为0。
这被称为0点问题 zero-point problem
解决方法:
- A smooth process can be performed by introducing prior probability distribution, which is known as Bayesian Estimation使用先验概率分布,也叫贝叶斯估计。
- an uniform distribution is used as the prior probability distribution, in which case, it is called Laplacian Correction默认先验概率分布为平均分布,叫做拉普拉斯校正。
朴素贝叶斯分类器
朴素
朴素刚才讲过了(献血 和 O型血,男性,学生那个例子)
假设x的特征属性(attributes)间相互独立
拟然只有一个特征的x时,直接算该x在数据集中的拟然度(条件概率)。
拟然多个特征的x时,计算x的各个特征的拟然度(条件概率)之积:
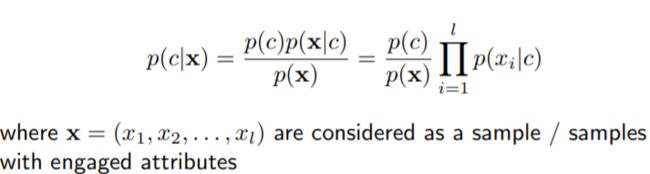
又由于同个训练集的观察结果相同:
·后验概率· 与 ·先验概率 乘 拟然度· 成正比
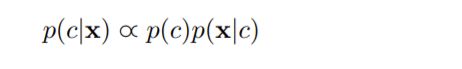
又由于大数定律:
大数定律(law of large numbers),又称大数定理,是一种描述当试验次数很大时所呈现的概率性质的定律。
这个定律可以作为之前例子中从 地球上已献血的人的比例 估作是 甲献血的先验概率 的依据
分类器
搬运:
朴素贝叶斯法,顾名思义,选择了贝叶斯方法构造分类器。输入依然是特征向量x,输出是类标记c。我们希望通过训练数据学习联合概率分布P(c∩x),这说明朴素贝叶斯属于生成模型。
具体又是学习c的先验概率和条件概率(拟然)P(x|c)。既然已经有训练数据,特征和对应的标签类别是已知的,所以根据统计可以很容易地知道c的先验概率。
而条件概率就比较棘手了,因为特征空间通常是高维的,所以在已知某个类别下的条件概率有好多个,所以我们做了一个特别重要的假设,叫做条件独立性假设:在类确定的条件下,用于分类的特征是条件独立的。
而朴素贝叶斯方法选择了最大后验概率作为策略,选择0-1函数作为损失函数。按照书中的推导,为了使期望风险最小化,应该使**已知输入特征(训练集)**的后验概率最大化。所以朴素贝叶斯的策略应该是结构风险最小化的策略,先验概率表示了模型的复杂度。
————————————————
原文链接:https://blog.csdn.net/zcg1942/article/details/81205770
例子
半朴素分类器 Semi-Naive Bayes Classifier
Semi-Naive Bayes allows dependencies between features
总有些特征之间不是完全独立的,因此将部分特征依赖
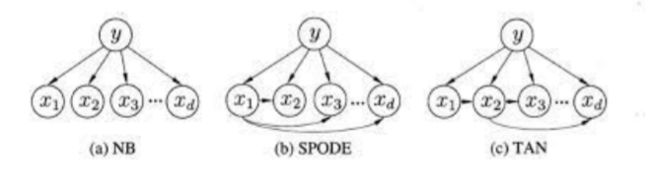
贝叶斯网络 Bayesian Network
The idea of Bayesian Graphical model is to factorise the joint probability distribution to more readable conditional probability distribution, which benefits the modelling algorithm (especially for semantic modelling)
使用有向无环图(Directed Acyclic Graph (DAG),Bayesian Graphical Model)表达特征间的依赖关系,将联合分布转变为更加可读的条件概率分布,宜于实现算法。
Lec10 聚类
无监督学习Unsupervised Learning
不给定label,只给一堆个体的特征,通过个体间特征表现出的关联度进行分析并学习。
聚类Clustering:
将一组观测值分配给不同的子集(簇,cluster),使同个子集内的观测值是相似的

图片来源:https://blog.csdn.net/u011511601/article/details/81951939
· 聚类的两个方法:
Agglomerative clustering (bottom-up): 层次聚类 hierarchical clustering
Divisive clustering (top-down): k均值聚类 k-means
· 如何评估聚类结果:
a smaller intra-cluster distance but a larger inter-cluster distance
尽可能使同个簇内的个体间距离较小,簇间的距离较大
层次聚类Hierarchical/Agglomerative Clustering
算法维护一个簇集合,
第一次循环,簇集合内每个簇中只有一个个体
第二次循环,对所有簇集合,将两个最邻近的簇合并
第三次循环,对所有簇集合,将两个最邻近的簇合并
…
一直循环到只剩下一个簇
由于层次聚类将小簇从下到上合并成大簇,所以层次聚类自底向上bottom-up
伪代码表示:

· 如何计算点m与点n之间距离:
····一般题目会给点间距离,PPT计算时用的是曼哈顿距离
· 如何计算簇C1与簇C2的距离:
- single linkage:
D is taken as the minimum distance between samples in sub-clusters
计算C1内各点到C2内各点的距离,选取最短的那个。 - complete linkage:
D is taken as the maximum distance between samples in sub-clusters
计算C1内各点到C2内各点的距离,选取最长的那个。 - average linkage:
D is taken as the average distance between each pair of samples in sub-clusters
计算C1内各点到C2内各点的距离,选取它们的平均数。
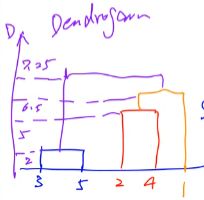
例子
给定距离矩阵(邻 接 矩 阵),按照average linkage求层次聚类(题目要求用啥方法就用啥方法):
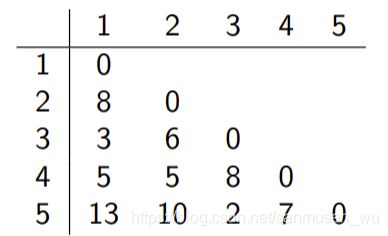
可以注意到除了被组合的两簇所在的行和列,其他行和列的值是不需要重新计算的,如:合并5,3后的新矩阵的前三行(0,8 0,5 5 0),减少重复计算

k均值聚类 k-means/Divisive Clustering
样本散布在特征空间内,随机设立k个组(先验,要多少设立多少),每组拥有一个中心Xk
算法维护这些中心点:
第一次循环,随机设置这些中心点的位置(最好互相离得不要太近,可以从样本中选)。
每次循环一开始时,重新计算每个样本到这些组中心点的距离,选择最近的中心点,将样本分配给最近的组中心点(拟分类)。
然后,求出每组中的样本的均值点,将该组的中心点更新为这些样本的均值点(更新中心点)。
再次循环,直到中心点和算出的均值点相同。
图片来源:https://blog.csdn.net/u011511601/article/details/81951939
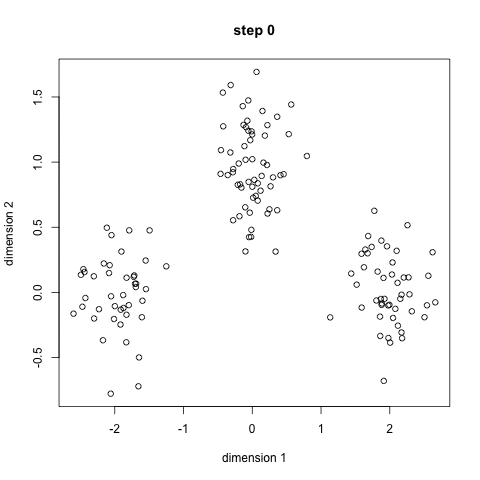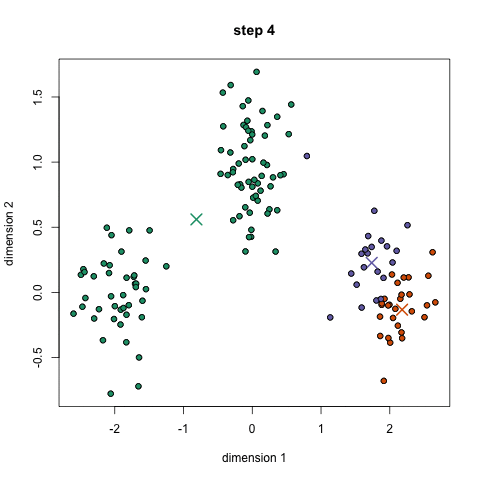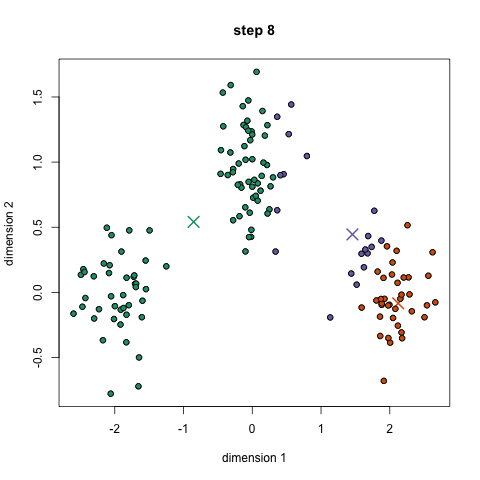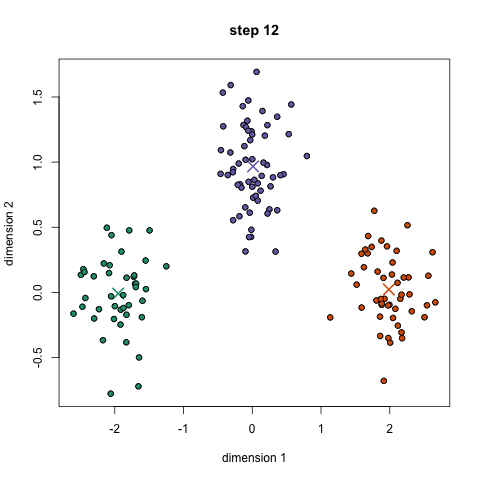
例子
给定7个点(1.0, 1.0), (1.5, 2.0), (3.0, 4.0), (5.0,7.0), (3.5, 5.0), (4.5, 5.0), (3.5, 4.5),使用k均值算法将其分成两类。这里使用的是曼哈顿距离(各维度距离之和)

高斯混合模型 Gaussian Mixture Model (GMM)
与k均值类似,但更包容,为了解决数据缺失或存在未发现特征的情况。
不再用”距离中心最短“硬性分割类别,而是用“有多大高斯分布概率属于这个类“的思想去分类
每个高斯分量对应一个组,假设数据点符合高斯分布,通过最大期望算法EM 找到每个组的高斯参数(即均值和标准差),进而求得每个组的高斯分布,从而得到组-masicayy
最大期望算法EM
分为期望和最大化期望步骤:
期望Expectation step: find the posterior probability according to current model
期望最大化Maximisation step: calculate the new modal parameters
算法维护k个类的k个高斯函数:
第一次循环,随机初始化这些高斯函数。
每次循环一开始时,重新计算每个样本根据高斯函数划分到那个类的的概率(拟分类)。
然后,求出每组中的样本的概率,重塑高斯函数使这个组的样本概率最大化(更新高斯函数)。
再次循环,直到每组内样本概率收敛。

评价GMM
-
模型拟然model likelihood
已知模型但未知参数,如:对于一个庞大的集,只知道符合高斯分布但不知道均值和方差,通过采样,可以获取部分子集的数据,然后通过最大似然估计来获得正态分布的均值与方差。
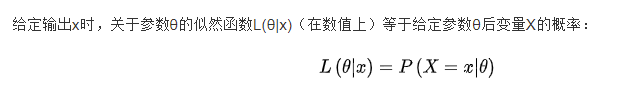
-
模型选择准则model selection criteria
·· AIC Akaike Information Criterion
AIC = 2k − 2LL
·· BIC Bayesian Information Criterion
BIC = k log N − 2LL
Lec11 非参数模型
· 什么是参数模型:
- 参数模型需要不断改变模型内的参数以达到学习的目的
如:拟合问题中的拟合线的表达式,分类问题中的类与类之间的分界线表达式,聚类问题中的每类的中心点位置等等 - 这些参数值换言之就是机器学习的结果,他们依靠循坏不断地更新参数值从而使模型趋于完善,使准确率变高。
非参数模型Non-parametric Modelling
· 什么是非参数模型:
- 非参数模型既是不需要在循环中更新某些参数的模型,并不是啥参数都没有的模型
- 非参数模型属于监督学习,它依靠已有的”训练集“中的特征值和标签,试图用这些已有的样本作为经验,分析只有特征值没有标签的测试集
- 与参数模型需要许多次循环更新参数不同,非参数模型学习的过程其实就是通过交叉验证选择一个表现最好的模型的过程。
· 非参数模型的优点:
- generality:不需要去琢磨究竟应该使用哪种学习方法,如何更新参数。完全依靠已有数据集。
- 不仅适用于单峰分布unimodal distributions,还适用于实际应用中更加多见的多峰分布multimodal distributions
- 已有数据集越大,就越能准确推断结果。
Central Limit Theorem (CLT):when independent random variables are added, their properly normalised sum tends toward a normal distribution even if the original variables themselves are not normally distributed.
· 非参数模型的不足:
- 已有数据集越大,每次测试集需要计算的时间就越久。
- 需要谨慎选择窗口大小(k和带宽)
- 对存储空间的较高需求
主要有俩方法:
- posterior probability estimation (Estimating P(wj |x)):k-Nearest Neighbour (k-NN)
- Estimating P(x|wj ) :Kernel Density Estimation (Parzen window)
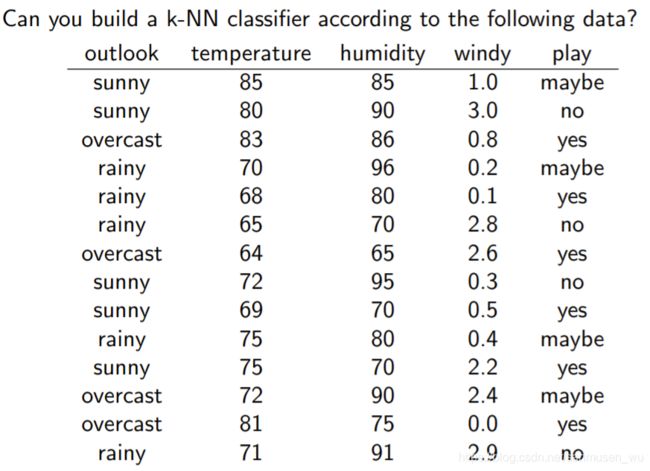
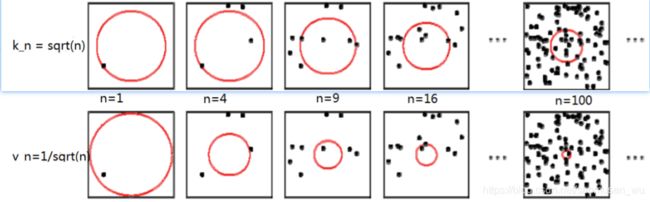
k-NN邻近算法(k-nearest neighbors algorithm k-NN)
将测试集数据x放在训练集的特征空间内,将其想象成一个不断变大的球,随着球的变大,他会挨个接触kn个离自己近的训练集,将这kn个训练集样本称为x的kn近邻样本(kn nearest-neighbours of x),看看这k个近邻样本中哪个label占比最大,x就属于那个label。
k是自己设立的值,每个x拥有k个近邻样本,学习的过程就是选择一个能使得模型效果最好的k的值的过程。(当然也可以直接确定k值,学校PPT用的是kn=√n)
两种情况:
- x点周围的训练集样本密集,x的近邻样本离自己非常近。
- x点周围的训练集样本稀疏,x需要持续找到k个距离自己稍远的近邻样本。
样题
Parzen窗(Parzen Window)核密度估计(Kernel Density Estimation)
核 Kernel
假设现有一数据,共n个样本,对这所有n个位置模拟各自的概率分布函数(右红),将其求和,可以近似得出概率密度函数(右蓝)
换言之就是根据结果推测概率:
将某个缝隙划分成许多小区域,然后把6个豆子撒在缝隙里(为什么是缝:因为下面这个图的数据是一维的所以用的是缝…),豆子的位置分别是-2.1, -1.4, -0.3, 1.8, 5.1, 6.1
什么是直方图(左):区域宽度为2,统计落在区域里的豆子数量,没有豆子的区域记为0,每个豆子代表该区域宽为2高为0.08的一段小矩形,将整个x轴的小矩形垒起来,最后形成了这个直方图。
什么是核函数估计(右): 区域宽度为一个极小值,统计落在区域(各自x值处)里的豆子数量,没有豆子的x值处记为0,每个豆子代表该x值处的核函数(一个x值处的核函数会影响它周围的x值的概率),将整个x轴的核函数垒起来,就是估计出来的密度分布。
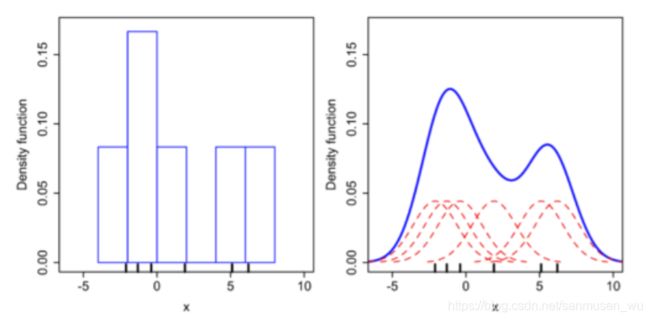
用来拟合红色的概率密度函数的模型就叫做核函数(Kernel)
核函数有许多种:

核需要满足三个条件:
- 非负,实数值,可积分
- Normality
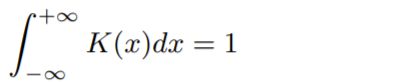
- Symmetry
带宽Bandwidth
数据量较少的情况下,直方图的bin(每个方块的宽度)的选择会影响直方图的表现,
(如:下图左边直方图bin比右边的小。左边7块,右边6块;左边双峰分布,右边却是单峰分布)
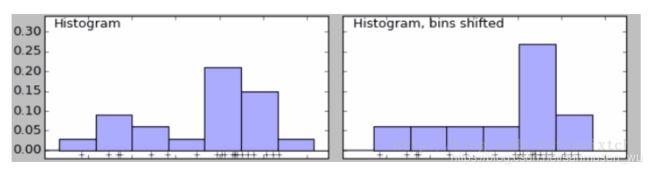
所以我们需要定义一个h,用来同样描述上述核函数的“宽度”(方差), 如宽度为h的一个核函数:K(x/h),
现在延展到多维:

通过下图可以看出:
h(带宽)越宽,概率分布函数越平滑
n(样本)越多,概率分布越接近真实值。样本无限多时带宽的大小就不那么重要了。
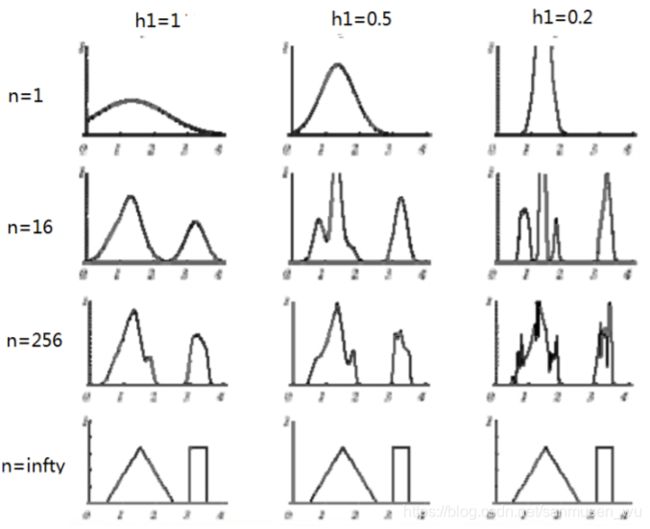
使用核密度解决分类问题
分别使用label为wi类型的点x估计那个类型的概率分布函数P(x|wi),再知道先验概率P(wi), 即可求得后验概率P(wi,x)
同样会有h大小取值问题
h的不同会影响非参数模型的效率,学习的过程就是选择一个能使模型表现最好的h。
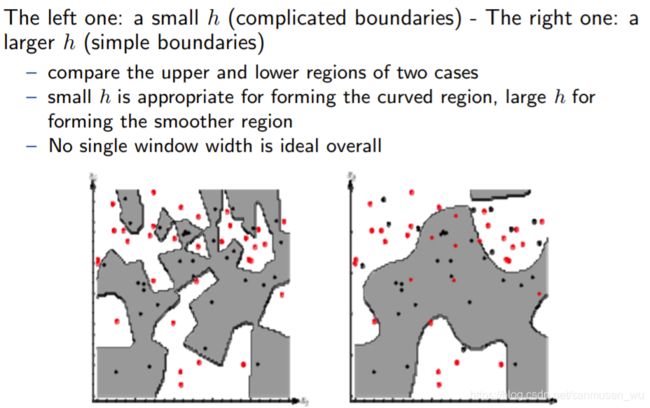
比较k近邻和核密度
k近邻:从一个点放大找邻居
![]()
Parzen窗口:把概率分布曲线划分成许多有颗粒度的小部分直方图,当小直方无限多时,就可以近似表现概率分布曲线
![]()
Lec12命题逻辑与Prolog
什么是逻辑Logic
logic包含:
· a well-defined syntax;
· a well-defined semantics; and
· a well-defined proof-theory
相关名词
· syntax:The syntax of logic defines the syntactically acceptable objects of the language, which are properly called well-formed formulae (wff ).
· semantics:The semantics of logic associate each formula with a meaning
· proof theory:The proof theory is concerned with manipulating formulae according to certain rules.
命题Propositional
是最简单抽象的逻辑,定义:一个命题要么为真T要么为假F,不能both。
比如:窗户是开着的。通过在句子前加上It’s true that…可以判断是否为合理的命题。
· atomic proposition原子命题:An atomic proposition is one whose truth or falsity does not depend on the truth or falsity of any other proposition
· propositional variables命题变量:使用小写字母代替命题,如:Let p be Boris Johnson is prime minister.
连结命题公式
将原子命题连结起来
Truth table真值表:表示组合命题的真假
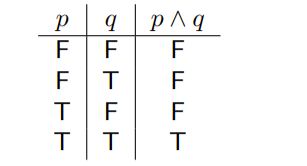
AND
OR
NOT
IMPLIES (IF … THEN …)
这些含有条件的命题被称为条件命题(conditional / implication of the originals)

· if φ is the formula p ⇒ q, then p is the antecedent of φ and q is the consequent
· the p ⇒ q means ‘if p is true, the q is true’. If p is false, then we don’t care about q and by default, make p ⇒ q evaluate to T in this case.

IFF( if and only if)

p ⇔ q
· biconditional operator:双向条件
it be true iff either:
- p and q are both true; or
- p and q are both false
复杂连结命题公式
· We can nest complex formulae as deeply as we want.
· We can use parentheses ‘(’,’)‘ to disambiguate formulae.

特殊命题公式
· Valuation重言式
又称为永真式,如果一个公式,对于它的任一解释下其真值(truth value)都为真,则为重言式。

- 重言式A formula is a tautology iff it is true under every valuation;
- 永真式A formula is consistent iff it is true under at least one valuation;
- 永假式A formula is inconsistent iff it is not made true under any valuation
命题公式的局限
coarse grained:粗粒度
premises:前提
conclusion:结论
因为粗粒度较大,命题公式没法表现出命题里蕴含的逻辑连结或推导关系

因此需要改进:
一阶逻辑FOL (First-Order Logic:Syntax)
术语Terms
The basic components of FOL are called terms.
FOL的基本组合被称为Terms
· constant常量
如: Let S be the set {1, 2, 3}
· variable变量
A variable of type T is a name that can denote any value in the set T.
· functions函数
输入某些量,返回某些量。每个函数都有函数符号(function symbol),通过使用函数符号和某些输入可以构造函数项(functional term)

谓语Predicates
谓词符号predicate symbols:操作符,用于表现对象间关系


如果谓语中包含变量,在不知道变量的解释(interpretation)的情况下没法得知谓语的真假,根据包含变量的数量来划分:
· A predicate that contains no variables(但是可能有常量) is a proposition命题
· Predicates of arity 1 are called properties属性
· Predicate that have arity 0 (i.e. take no arguments(无参数)) are called primitive propositions原始命题
量词Quantifiers
量词用于量化(quantifiers)物体,all/exist这种


Examples:
∃m : Monitor • MonitorState(m, ready)
∀m, n : Person • ¬Superior (m, n)
∀m : Person • ¬∃n : Person • Superior (m, n)
注意点
用任意和存在量化(universal quantification)可以与结合(conjunction)起来的公式互相转化


可判定性Decidability
(NP问题)
A formula of FOL that is true under all interpretations is said to be valid。
将任意条件下都成立的FOL认为是特殊的有效FOL(类似于重言式tautologies)。
With out using truth table, is there any other procedure that we can use, that will be guaranteed to tell us, in a finite amount of time, whether a FOL formula is, or is not, valid?
不使用真值表,能够在有限时间内确定一个FOL是否是有效FOL
The answer is no.
没法判别
FOL is for this reason said to be undecideable.
因此FOL拥有不可判别性