分治法(快速排序、归并排序)
基础知识
1.分治法:divide and conquer ,D&C,将原问题划分为若干个规模较小而结构与原问题一致的子问题;递归地解决这些子问题,然后再合并其结果,得到原问题的解。
2. 分治算法优点:容易确定运算时间。T(n)=3T(n/2)+f(n)
3.归并排序重在合并,从中间划分,左边排序(2,4,6,8),右边排序(1,3,5,7),合并(1,2,3,4,5,6,7,8)
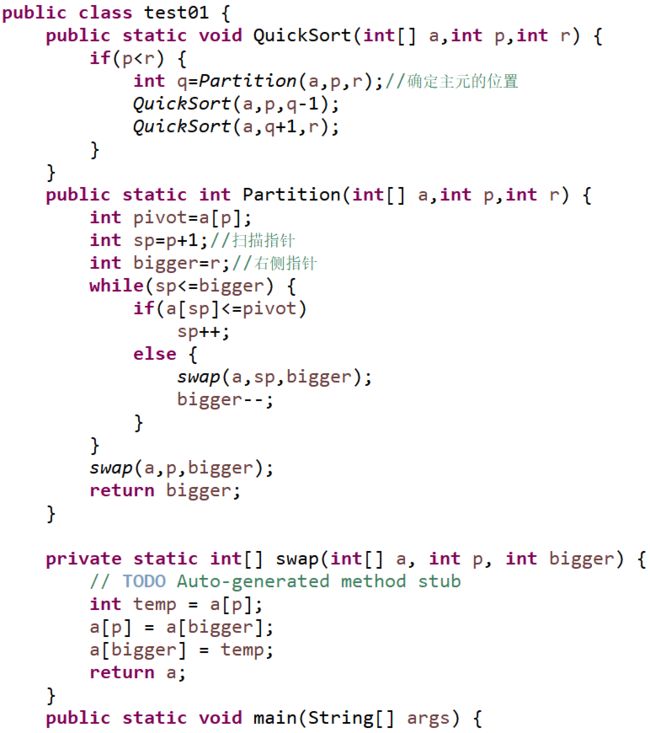
4.快速排序重在划分,分解:数组A[p..r]被划分为两个子数组A[p. .q-1]和A[q+1,r],使得A[q]为大小居中的数,左侧A[p. .q-1]中的每个元素都小于等于它,而右侧A[q+1,r]中的每个元素都大于等于它。其中计算下标q也是划分过程的一部分。
QuickSort(int[] a,int p,int r) {
if(p5.快速排序分区算法:
(1)一遍单向扫描法
(2)双向扫描法
双向扫描的思路是,头尾指针往中间扫描,从左找到大于主元的元素,从右找到小于等于主元的元素二者交换,继续扫描,直到左侧无大元素,右侧无小元素
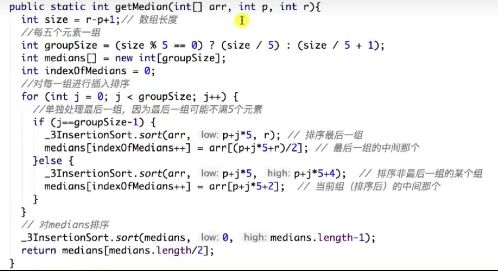
(3)优化(三点中值法)
(4)绝对中值法
所有数据,五个一组,每一组插入排序并取中间值
n<=8用插入排序快,列表较短时用插入排序
6.归并排序
归并排序(Merge Sort)算法完全依照了分治模式:
分解:将n个元素分成各含n/2个元素的子序列;
解决:对两个子序列递归地排序;
合并:合并两个已排序的子序列以得到排序结果
和快排不同的是归并的分解较为随意,重点是合并,开辟辅助空间
7.调整数组顺序使奇数位于偶数前面
【问题描述】输入一个整数数组,调整数组中数字的顺序,使得所有奇数位于数组的前半部分, 所有偶数位于数组的后半部分。要求时间复杂度为O(n)。
【算法1】使用归并排序的思想,开辟辅助空间,从左到右扫描,遇到奇数从左开始放,遇到偶数从右开始放O(n)。
【算法2】使用快速排序的思想,两个指针,一个从左开始扫描,一个从右开始扫描,左边扫描到偶数停,右边扫描到奇数停,然后进行交换。
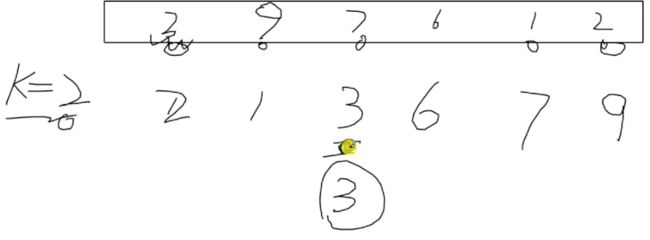
8.第k个元素
【问题描述】以尽量高的效率求出一个乱序数组中按数值顺序的第K个元素值
【算法】快排分区算法,主元的下标=它在最终序列中的位置(第几个)
【代码】
9.超过一半的数字
【问题描述】数组中有一个数字出现的次数超过了数组长度的一半,找出这个数字。
【算法1】排序后返回arr[n/2],nlg(n)
【算法2】顺序排序O(n)
【算法3】寻找发帖的水王,消除法,遇到不同的数就消除,两两不同的就消除
10.出现次数恰好为一半
【算法】扫描一遍数组就解决问题:
水王占总数的一半,说明总数必为偶数:
假设隔一 个数就是水王的id, 两两不同最后一定会消减为0
水王可能是最后一个元素,每次扫描的时候,多一个动作,和最后一个元素做比较,单独计数,计数恰为一半
如果不是,计数不足一半,那么去掉最后一个元素,水王就是留下的那个candidate
11.最小id可用
在非负数组(乱序)中找到最小的可分配的id (从1开始编号) ,数据量1000000
12.合并有序数组
【问题描述】给定两个排序后的数组A和B ,其中A的未端有足够的缓冲空间容纳B。编写一个方法,将B合并入A并排序
【算法】归并排序,current的下标=p1+p2-1
13.逆序对个数
【问题描述】一个数列,如果左边的数大,右边的数小,则称这两个数为一个逆序对。求出一个数列中有多少个逆序对。
nlg(n)是快排和归并
【算法】merge过程中,只要抓右侧的数,那么就有逆序对数量是左侧队伍的元素个数
【代码】