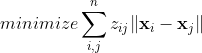论文阅读：在Stiefel流形上的黎曼优化

原文：EFFICIENT RIEMANNIAN OPTIMIZATION ON THE STIEFEL MANIFOLD VIA THE CAYLEY TRANSFORM

 

Citing: https://arxiv.org/pdf/2002.01113.pdf

目录

摘要 

1 简介

2 相关工作

3 基础知识

3.1 黎曼流形

定义1：黎曼流形

定义2：测地、幂映射和收缩映射

定义3：平行运输和媒介运输

3.2 Stiefel 流形

3.2.1 利用Cayley变换交替更新参数

4 算法

4.1  Cayley SGD

4.2 Cayley Adam

---

摘要 

在参数矩阵上严格执行正交约束在深度学习中显示出了优势。这相当于Stiefel流形上的黎曼优化，但是计算成本很高。我们提出了两个主要贡献：（1）基于迭代Cayley变换的新的高效收缩映射，用于优化更新；（2）基于Stiefel流形上的动量投影和Cayley变换的组合的隐式向量传输机制。

这得到了两个新的优化算法：带momentum的Cayley-SGD和Cayley-ADAM（在Stiefel流形上的），且理论上收敛。CNN训练实验表明，这两种优化算法：（a）相对于现有的强制CNN参数正交性的方法，每次迭代使用较少的运行时间；（b）在不影响CNN性能的情况下，比标准SGD和ADAM算法更快的收敛速度。这两种优化算法也被证明可以减少RNN中优化酉转移矩阵的训练时间。

1 简介

正交性最近引起了人们的兴趣，因为在深度神经网络的参数矩阵上强制正交具有显著的优势。对于CNN，Bansal等人表明，正交性约束提高了准确性，并给出了更快的经验收敛速度；Huang等人表明，正交性稳定了训练中神经激活的分布；Cogswell等人表明，正交性减少了过拟合，并提高了泛化。对于RNNs，正交隐矩阵缓解了消失和爆炸梯度问题。Stiefel流形上的黎曼优化是正交约束下优化的一个优雅框架，该流形代表了相同大小的所有正交矩阵的集合。但其高昂的计算成本限制了其应用。

通过正则化间接将正交性纳入深度学习并不能保证参数矩阵的精确正交性。为了解决上述局限性，我们的第一个主要贡献是基于Cayley变换的收缩映射的有效估计，用于更新Stiefel流形上的大型非平方参数矩阵。我们指定了一种有效的迭代算法来估算Cayley变换，该算法只包含少量矩阵乘法，而闭式的Cayley变换需要昂贵的矩阵逆运算。本文从理论和实证两方面验证了收缩映射的有效性。

我们的第二个主要贡献是通过考虑我们在Stiefel流形上优化的动量来提高训练的收敛速度。我们推导了一种在流形的切空间之间移动切向量的新方法，而不是使用标准的并行传输。具体地说，我们将斯蒂费尔流形视为欧氏空间的子流形。这允许将矢量传输（Absil等人，2009）表示为切线空间上的投影。正如我们所展示的，由于Cayley变换隐式地将梯度投影到切线空间，动量更新导致隐式矢量传输。因此，我们首先计算欧氏空间中动量和梯度的线性组合，然后使用Cayley变换更新网络参数，而不显式执行向量传输。

我们将上述两个贡献应用于将标准SGD和ADAM推广到Stiefel流形，得到了两个新优化算法，即Cayley-SGD与Cayley-ADAM。

在CIFAR-10和CIFAR-100数据集上的实验表明，虽然传统SGD和Adam在每个epoch上花费的时间较少，但它们在收敛花费的epoch比Cayley-SGD和Cayley-ADAM多。与其它考虑正交性的现有优化方法（如极分解、QR分解或闭式Cayley变换）相比，我们的方法运行速度更快，在图像分类中产生同样好甚至更好的性能。最后，我们将上述两个贡献应用于RNN的培训。Wisset等人提出了全容量酉RNN，该RNN使用闭式Cayley变换更新隐藏到隐藏的转移矩阵。相比之下，我们的训练在不影响性能的情况下，每次迭代花费的运行时间更少。

2 相关工作

本节回顾了密切相关的工作，可大致分为两组：正交正则化和黎曼优化。

正则化方法可以分为严格执行正交性的硬正则化方法和软正则化方法。硬正则化在计算上很昂贵，因为需要昂贵的特征值分解。Huang等人（2018a）推导了硬正则化的一个闭式解，该解也需要特征值分解。软正则化介绍了互相干正则化和谱限制等距正则化；然而，这些正则化不能完全保证正交性。

黎曼优化保证了解的正交性约束。例如，Cho&Lee用Grassmann流形上的黎曼优化替换了CNN中的批量归一化层，其中参数是归一化的，但不是正交归一化的。此外，Helfrich等人（2017年）对酉矩阵组进行黎曼优化，以稳定RNN训练，但他们的技术无法应用于非平方参数矩阵。

黎曼优化的关键挑战是，幂映射（估计下一个更新点的标准步骤）在Stiefel流形上的计算代价很高。有些方法用伪测地收缩（pseudo-geodesic retraction）代替幂映射。例如，使用基于投影的方法将梯度映射回Stiefel流形，该流形依赖于计算昂贵的SVD分解。其他方法基于闭式Cayley变换，但需要昂贵的矩阵求逆。

3 基础知识

3.1 黎曼流形

定义1：黎曼流形

黎曼流形是一个带有黎曼度量的光滑流形，度量定义为切线空间上每个点x的内积，即 。

定义2：测地、幂映射和收缩映射

测地线是流形上局部最短的曲线。幂映射将切向量映射到流形上。表示流形上的一条测地线。收缩映射定义为流形上的平滑映射，如果且，其中表示的导数，表示在上定义的单位映射。很容易证明任何幂映射都是收缩映射。由于计算一个幂映射通常是昂贵的，收缩映射通常被用作一种有效的替代方法。

定义3：平行运输和媒介运输

平行传输是一种在保持范数不变的情况下沿流形上的测地线平移向量的方法，向量传输是定义在流形的收缩映射上的平滑映射：。通常，矢量传输在计算上是平行传输的有效替代方案。

3.2 Stiefel 流形

Stiefel流形是一种黎曼流形，由所有正交矩阵组成，之后记为。我们认为是欧氏空间中的嵌入子流形。因此，黎曼度量是欧几里德度量：，其中是映射的切向量，定义为：

注：Stiefel 流形在上的切空间的要求即 ，即 ，即

矩阵到上的投影可以计算为：

 给定目标函数在欧几里德空间中处的导数，我们可以使用等式（2）给出的计算Stiefel流形上的黎曼梯度作为对的投影。因此，黎曼流形上f的优化可以计算如下。首先，在中计算;其次，将动量传输到当前切线空间，并将其与当前的伊曼梯度线性组合，以更新动量。最后，沿流形上的曲线更新新参数，初始方向为。

虽然幂映射和并行传输可以用来更新黎曼流形优化中的参数和动量，但在Stiefel流形上，它们在计算上是不可行的。在下一节中，我们将详细说明计算效率较高的备选方案。

3.2.1 利用Cayley变换交替更新参数

Cayley变换使用负对称矩阵计算Stiefel流形上的参数曲线。Cayley变换的闭式如下：

其中，W是负对称矩阵，即、 X位于Stiefel流形上，是表示曲线长度的参数。很容易验证：

根据定义2和等式1给出的Stiefel流形切线空间的定义，Cayley变换是斯蒂费尔流形上的一种有效收缩映射。如等式2所示，通过选择，其中

我们可以看到Cayley变换隐式地在切线空间上投影梯度作为其初始方向。因此，Cayley变换可以表示Stiefel流形上参数矩阵的更新。 

然而，闭式Cayley变换需要计算昂贵的矩阵求逆，这在大型深层神经网络中无法有效执行。我们的第一个贡献是Cayley变换的迭代估计，它只有效地使用矩阵乘法。我们用以下定点迭代表示Cayley变换：

4 算法

本节详细说明了我们的Cayley SGD和Cayley ADAM算法。这两种方法都代表了Stiefel流形上的有效黎曼优化，该流形由两个主要步骤组成。由于Cayley变换隐式地将梯度和动量向量投影到切线空间上，我们首先将上一次迭代的动量与目标函数在当前点处的随机梯度（记为）的线性组合。然后，我们使用迭代Cayley变换根据更新的动量估计下一个优化点。这是用来将传统的带动量和ADAM算法的SGD推广到我们在Stiefel流形上的两个新的黎曼优化，如第4.1节和第4.2节所述。 

4.1  Cayley SGD

我们将heavy ball(HB)动量更新推广到Stiefel流形。理论上，它可以表示为：

4.2 Cayley Adam

ADAM是一种新的随机目标函数一阶优化方法。它估计自适应低阶矩，并使用自适应学习率。该算法结合了AdaGrad（在稀疏梯度情况下表现良好）和RMSProp（在非平稳情况下表现良好）的优点。

我们通过对vanilla ADAM进行三次修改，将ADAM推广到Stiefel流形。首先，我们用Stiefel流形上相应的梯度和动量替换标准梯度和动量，如第4.1节所述。其次，我们使用流形自适应学习率，为参数矩阵中的所有条目分配相同的学习率，如（Absil等人，2009年）。第三，我们使用Cayley变换来更新参数。