神经网络中的权重初始化

目录

权重的初始值

1 可以将权重设置为0吗？

2 隐藏层的激活值的分布（sigmoid函数为例）

3 ReLU的权重初始值

4 总结

---

权重的初始值

在神经网络的学习中，权重的初始值特别重要。实际上，设定什么样的权重初始值，经常关系到神经网络的学习能否成功。接下来介绍下权重初始值的推荐值

1 可以将权重设置为0吗？
 

如果我们把权重初始值全部设为0以减小权重的值，会怎么样呢？从结论来说，将权重初始值设为0不是一个好主意。事实上，将权重初始值设为0的话，将无法正确进行学习。

为什么不能将权重初始值设为0呢？严格地说，为什么不能将权重初始值设成一样的值呢？这是因为在误差反向传播法中，所有的权重值都会进行相同的更新。比如，在2层神经网络中，假设第1层和第2层的权重为0。这样一来，正向传播时，因为输入层的权重为0，所以第2层的神经元全部会被传递相同的值。第2层的神经元中全部输入相同的值，这意味着反向传播时第2层的权重全部都会进行相同的更新（回忆一下“乘法节点的反向传播的内容）。因此，权重被更新为相同的值，并拥有了对称的值（重复的值）。这使得神经网络拥有许多不同的权重的意义丧失了。为了防止“权重均一化”（严格地讲，是为了瓦解权重的对称结构），必须随机生成初始值。

2 隐藏层的激活值的分布（sigmoid函数为例）

观察隐藏层的激活值 （激活函数的输出数据）的分布，可以获得很多启发。
这里要做的实验是，向一个5层神经网络（激活函数使用sigmoid函数）传入随机生成的输入数据，用直方图绘制各层激活值的数据分布。这个实验参考了斯坦福大学的课程CS231n 。

   代码如下：

# coding: utf-8
import numpy as np
import matplotlib.pyplot as plt


def sigmoid(x):
    return 1 / (1 + np.exp(-x))


def ReLU(x):
    return np.maximum(0, x)


def tanh(x):
    return np.tanh(x)
    
input_data = np.random.randn(1000, 100)  # 1000个数据
node_num = 100  # 各隐藏层的节点（神经元）数
hidden_layer_size = 5  # 隐藏层有5层
activations = {}  # 激活值的结果保存在这里

x = input_data

for i in range(hidden_layer_size):
    if i != 0:
        x = activations[i-1]

    # 改变初始值进行实验！
    w = np.random.randn(node_num, node_num) * 1
    # w = np.random.randn(node_num, node_num) * 0.01
    # w = np.random.randn(node_num, node_num) * np.sqrt(1.0 / node_num)
    # w = np.random.randn(node_num, node_num) * np.sqrt(2.0 / node_num)


    a = np.dot(x, w)


    # 将激活函数的种类也改变，来进行实验！
    z = sigmoid(a)
    # z = ReLU(a)
    # z = tanh(a)

    activations[i] = z

# 绘制直方图
for i, a in activations.items():
    plt.subplot(1, len(activations), i+1)
    plt.title(str(i+1) + "-layer")
    if i != 0: plt.yticks([], [])
    # plt.xlim(0.1, 1)
    # plt.ylim(0, 7000)
    plt.hist(a.flatten(), 30, range=(0,1))
plt.show()

 

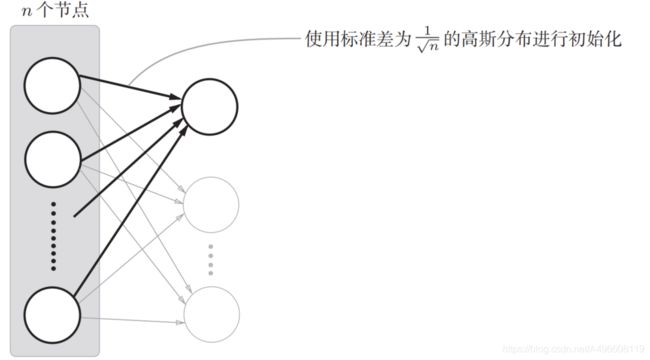
        这里假设神经网络有5层，每层有100个神经元。然后，用高斯分布随机生成1000个数据作为输入数据，并把它们传给5层神经网络。激活函数使用sigmoid函数，各层的激活值的结果保存在activations变量中。这个代码段中需要注意的是权重的尺度。虽然这次我们使用的是标准差为1的高斯分布，但实验的目的是通过改变这个尺度（标准差），观察激活值的分布如何变化。现在，我们将保存在activations中的各层数据画成直方图。
  

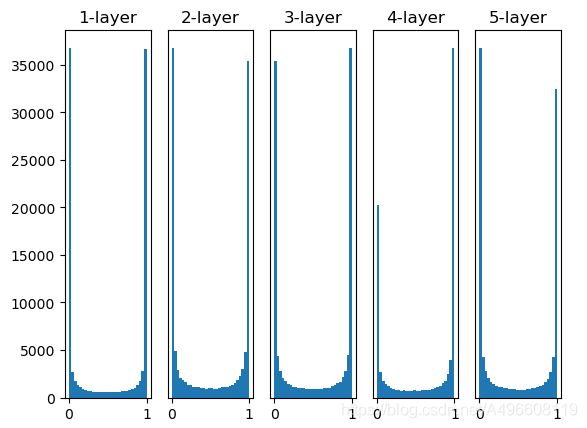使用标准差为1的高斯分布作为权重初始值时的各层激活值的分布
从图6-10可知，各层的激活值呈偏向0和1的分布。这里使用的sigmoid函数是S型函数，随着输出不断地靠近0（或者靠近1），它的导数的值逐渐接
近0。因此，偏向0和1的数据分布会造成反向传播中梯度的值不断变小，最后消失。这个问题称为梯度消失（gradient vanishing）。层次加深的深度学习中，梯度消失的问题可能会更加严重。
 

下面，将权重的标准差设为0.01，进行相同的实验。实验的代码只需要把设定权重初始值的地方换成下面的代码即可：（对一开始的完整代码进行修改）

    # 改变初始值进行实验！
    #w = np.random.randn(node_num, node_num) * 1
    w = np.random.randn(node_num, node_num) * 0.01
    # w = np.random.randn(node_num, node_num) * np.sqrt(1.0 / node_num)
    # w = np.random.randn(node_num, node_num) * np.sqrt(2.0 / node_num)

 

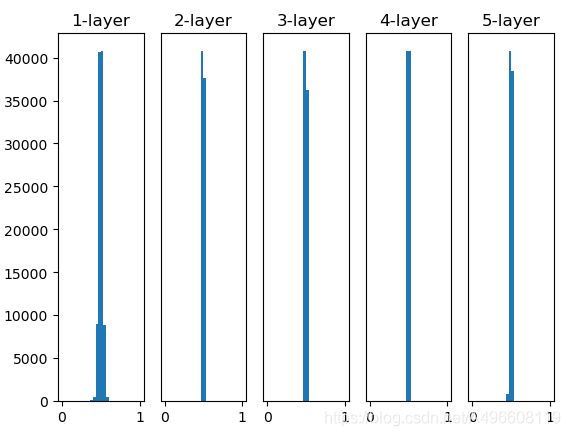
这次呈集中在0.5附近的分布。因为不像刚才的例子那样偏向0和1，所以不会发生梯度消失的问题。但是，激活值的分布有所偏向，说明在表现力
上会有很大问题。为什么这么说呢？因为如果有多个神经元都输出几乎相同的值，那它们就没有存在的意义了。比如，如果100个神经元都输出几乎相
同的值，那么也可以由1个神经元来表达基本相同的事情。因此，激活值在分布上有所偏向会出现“表现力受限”的问题。
 

各层的激活值的分布都要求有适当的广度。为什么呢？因为通过在各层间传递多样性的数据，神经网络可以进行高效的学习。反
过来，如果传递的是有所偏向的数据，就会出现梯度消失或者“表现力受限”的问题，导致学习可能无法顺利进行。

我们尝试使用Xavier Glorot等人的论文 [9]中推荐的权重初始值（俗称“Xavier初始值”）。现在，在一般的深度学习框架中， Xavier初始值已被作为标准使用。比如， Caffe框架中，通过在设定权重初始值时赋予xavier参数，就可以使用Xavier初始值。
  Xavier的论文中 推导出的结论是，如果前一层的节点数为n，则初始值使用标准差为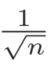 的分布 

使用Xavier初始值后，前一层的节点数越多，要设定为目标节点的初始值的权重尺度就越小。现在，我们使用Xavier初始值进行实验。进行实验的代码只需要将设定权重初始值的地方换成如下内容即可（因为此处所有层的节点数都是100，所以简化了实现）。（对一开始的完整代码进行修改）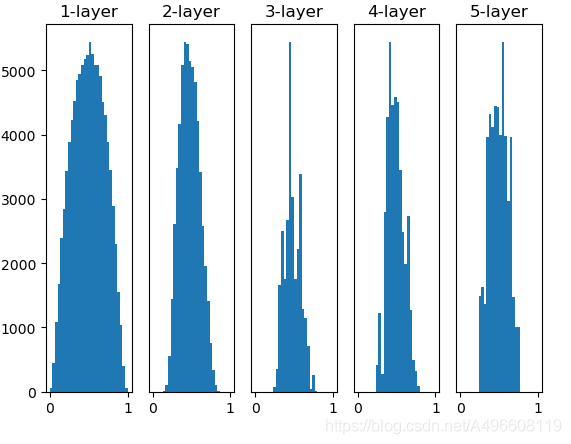

从这个结果可知，越是后面的层，图像变得越歪斜，但是呈现了比之前更有广度的分布。因为各层间传递的数据有适当的广度，所以sigmoid函数的表现力不受限制，有望进行高效的学习。
 

上图的分布中，后面的层的分布呈稍微歪斜的形状。如果用tanh函数（双曲线函数）代替 sigmoid函数，这个稍微歪斜的问题就能得到改善。实际上，使用 tanh函数后，会呈漂亮的吊钟型分布。 tanh
函数和sigmoid函数同是S型曲线函数，但tanh函数是关于原点(0, 0)对称的S型曲线，而 sigmoid函数是关于(x, y)=(0, 0.5)对称的S型曲线。众所周知，用作激活函数的函数最好具有关于原点对称的性质。

3 ReLU的权重初始值

Xavier初始值是以激活函数是线性函数为前提而推导出来的。因为sigmoid函数和 tanh函数左右对称，且中央附近可以视作线性函数，所以适
合使用Xavier初始值。但当激活函数使用ReLU时，一般推荐使用ReLU专用的初始值，也就是Kaiming He等人推荐的初始值，也称为“He初始值” 。
当前一层的节点数为n时， He初始值使用标准差为 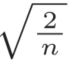的高斯分布。当Xavier初始值是 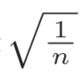时，（直观上）可以解释为，因为ReLU的负值区域的值为0，为了使它更有广度，所以需要2倍的系数。

现在来看一下激活函数使用ReLU时激活值的分布。我们给出了3个实验的结果（图6-14），依次是权重初始值为标准差是0.01的高斯分布（下文简写为“std = 0.01”）时、初始值为Xavier初始值时、初始值为ReLU专用的“He初始值”时的结果。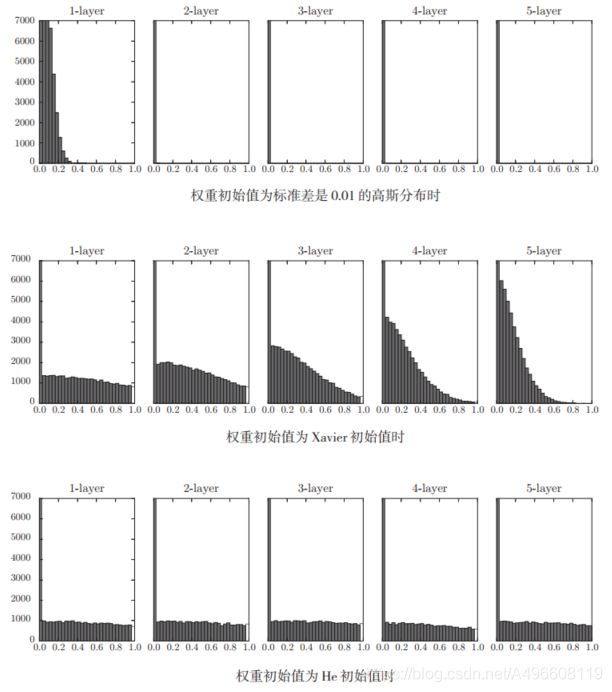

观察实验结果可知，当“std = 0.01”时，各层的激活值非常小 A。神经网络上传递的是非常小的值，说明逆向传播时权重的梯度也同样很小。这是很严重的问题，实际上学习基本上没有进展。
接下来是初始值为Xavier初始值时的结果。在这种情况下，随着层的加深，偏向一点点变大。实际上，层加深后，激活值的偏向变大，学习时会出现梯度消失的问题。而当初始值为He初始值时，各层中分布的广度相同。由于即便层加深，数据的广度也能保持不变，因此逆向传播时，也会传递合适的值
 

4 总结

总结一下，当激活函数使用ReLU时，权重初始值使用He初始值，当激活函数为 sigmoid或 tanh等S型曲线函数时，初始值使用Xavier初始值。这是目前的最佳实践。
 

综上，在神经网络的学习中，权重初始值非常重要。很多时候权重初始值的设定关系到神经网络的学习能否成功。权重初始值的重要性容易被忽视，
而任何事情的开始（初始值）总是关键的，因此在结束本节之际，再次强调一下权重初始值的重要性。