C++ opencv曲线拟合

简介：此问题是在做旋转模板匹配的时候，选择最好的匹配结果时产生的。查找资料发现多项式拟合问题可以变成一个超定方程的求解问题，而opencv中本身有一个cv::solve()函数可以求解线性方程组，因此对于大多数用到opencv又要进行曲线拟合的地方都可以参考此处的求解过程来解决。

1. 问题：

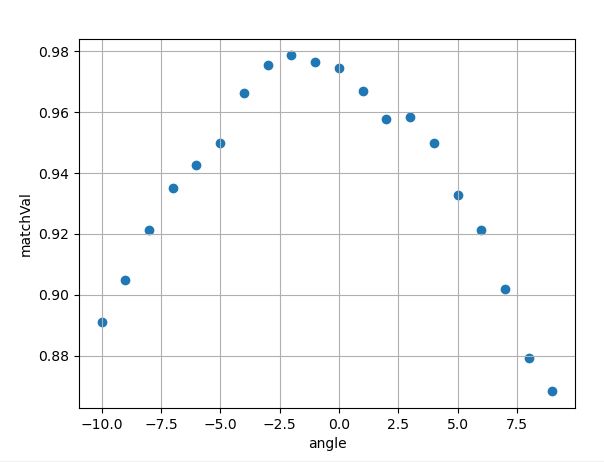
原始数据是一些离散的散点，下图是用matplotlib的plot方法画出来的，我想得到下图中最高处附近的近似的曲线方程，以得到一个最大值和最大值对应的横坐标。从下图看，在最高处附近很像一条抛物线，那就用2次函数去拟合最高处附近的曲线看看效果

2. 分析

二次函数的一般形式为$f(x)=a_0+a_{1}x+a_2{x}^2$,二次函数由$a_0,a_1,a_2$完全决定，这样只需要三组$(x,f(x))$的数据我们就可以求出$f(x)$的表达式。例如现在我们获得了三组数据，$(1,6),(2,11),(3,18)$,写成方程组的形式就是
$$\begin{gathered} a_0+a_1+a2=6 \\ {a}_0+2a_1+4a_2=11 \\ {a}_0+3a_1+9a_2=18 \end{gathered}$$
求解这个线性方程组就可以得到我们需要的二次方程，很容易求出来$a_0=3,a_1=2,a_2=1,即：f(x)=3+2x+x^2$。
在实际的情况下我们观测获得的数据并不是绝对准确的，也就是存在偏差，当数据足够多时就可以去除很大一部分随机误差，但是当方程数超过未知数的个数时，怎么求解呢？这就要引入下面超定方程的知识了。

3. 超定方程：

设方程Ax = b.根据有效的方程个数和未知数的个数，可以分为以下3种情况：

1. rank(A) < n，也就是说方程个数小于未知数的个数，约束不够，方程存在无数组解，

2. rank(A) = n 方程个数等于未知数的个数， 方程存在唯一的精确解，解法通常有消元法，LU分解法

3. rank(A) > n，方程个数多于未知数个数，这个时候约束过于严格，没有精确解，这种方程又称之为超定方程。通常工程应用都会遇到这种情况，找不到精确解的情况下，选取最优解，这个最优解，又称之为最小二乘解。

超定方程定义：

设方程组$Ax=b$ 中，$A=(a_{ij}{)}_{m\times n}$ ,$b$是$m$维已知向量，$x$是n维解向量，当$m>n$,即方程个数大于自变量个数时，称此方程组为超定方程组。

• 最小二乘解的定义：

记 $r=b-Ax$,称使$||r|{|}_2^2$ 最小的解$x^{\ast }$ 为方程组$Ax=b$ 的最小二乘解。

• 定理：

$x^{\ast }$ 是 $Ax=b$ 的最小二乘解的充要条件是：$x^{\ast }$ 是$A^{T}Ax=A^{T}b$的解。

4. 二次曲线拟合：

• 待拟合点：angle为横坐标，matchVal为纵坐标。

angle = { -10.,  -9.,  -8.,  -7.,  -6.,  -5.,  -4.,  -3.,  -2.,  -1.,   0.,
		 1.,   2.,   3.,   4.,   5.,   6.,   7.,   8.,   9. };
matchVal = { 0.890928, 0.904723, 0.921421, 0.935007, 0.94281 , 0.949828,
		   0.966265, 0.975411, 0.978693, 0.97662 , 0.974468, 0.967101,
		   0.957691, 0.958369, 0.949841, 0.932791, 0.9213  , 0.901874,
		   0.879374, 0.868257 };

• 散点图：

• 数学过程：
  设$f(x)=a_0+a_{1}x+a_2{x}^2$，则$Ax=b$中

$A=\left(\begin{array}{ccc}1& -10& 100\\ 1& -9& 81\\ 1& -8& 64\\ 1& -7& 49\\ 1& -6& 36\\ 1& -5& 25\\ 1& -4& 16\\ 1& -3& 9\\ 1& -2& 4\\ 1& -1& 1\\ 1& 0& 0\\ 1& 1& 1\\ 1& 2& 4\\ 1& 3& 9\\ 1& 4& 16\\ 1& 5& 25\\ 1& 6& 36\\ 1& 7& 49\\ 1& 8& 64\\ 1& 9& 81\end{array}\right)$,$x=\left(\begin{array}{c}{a}_0\\ a_1\\ a_2\end{array}\right)$, $b=\left(\begin{array}{c}0.890928\\ 0.904723\\ 0.921421\\ 0.935007\\ 0.94281\\ 0.949828\\ 0.966265\\ 0.975411\\ 0.978693\\ 0.97662\\ 0.974468\\ 0.967101\\ 0.957691\\ 0.958369\\ 0.949841\\ 0.932791\\ 0.9213\\ 0.901874\\ 0.879374\\ 0.868256\end{array}\right)$
构造$A^{T}Ax=A^{T}b$，求解此线性方程组就可以得到最小二乘解，也就得到我们需要的二次方程了。

5. python 实现：

import cv2 as cv
import numpy as np
import matplotlib.pyplot as plt
#%matplotlib
x = np.array([-10.,  -9.,  -8.,  -7.,  -6.,  -5.,  -4.,  -3.,  -2.,  -1.,   0.,
         1.,   2.,   3.,   4.,   5.,   6.,   7.,   8.,   9.], np.float)
y = np.array([0.890928, 0.904723, 0.921421, 0.935007, 0.94281 , 0.949828,
       0.966265, 0.975411, 0.978693, 0.97662 , 0.974468, 0.967101,
       0.957691, 0.958369, 0.949841, 0.932791, 0.9213  , 0.901874,
       0.879374, 0.868257], np.float)

A = np.zeros((len(x), 3)) #构造一个范德蒙德矩阵
A[:,0] = 1
A[:,1] = x
A[:,2] = x**2

c = np.matmul(A.T, A)
d = np.matmul(A.T, y)

_,result = cv.solve(c,d)

y2 = result[0] + result[1]*x + result[2] * (x**2)

plt.grid(True)
plt.xlabel("angle")
plt.ylabel("matchVal")
plt.scatter(x,y)
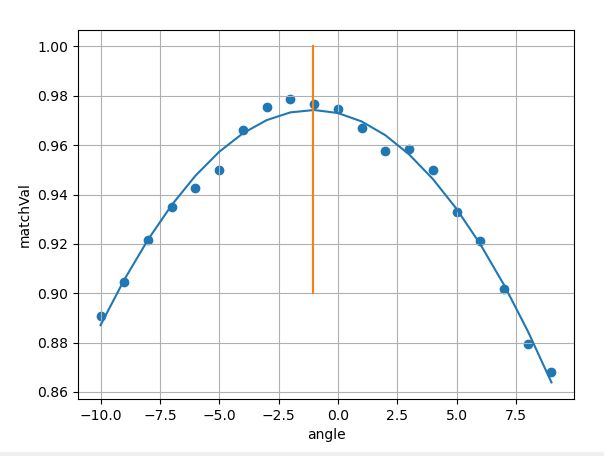
plt.plot(x,y2)
plt.plot( (-result[1]/result[2]/2,-result[1]/result[2]/2), (0.9,1))
print("拟合方程：f(x) = {} + ({}*x) + ({}*x^2)".format(result[0],result[1],result[2]))

• 输出结果：

拟合方程：f(x) = [0.97301156] + ([-0.00231144]*x) + ([-0.00109041]*x^2)

• 拟合结果：
  

6. C++实现：

#include 
int fitCurve(std::vector<double> x, std::vector<double> y)
{
	//columns is 3, rows is x.size()
	cv::Mat A = cv::Mat::zeros(cv::Size(3, x.size()), CV_64FC1);
	for (int i = 0; i < x.size(); i++)
	{
		A.at<double>(i, 0) = 1;
		A.at<double>(i, 1) = x[i];
		A.at<double>(i, 2) = x[i] * x[i];
	}
	
	cv::Mat b = cv::Mat::zeros(cv::Size(1, y.size()), CV_64FC1);
	for (int i = 0; i < y.size(); i++)
	{
		b.at<double>(i, 0) = y[i];
	}

	cv::Mat c;
	c = A.t() * A;
	cv::Mat d;
	d = A.t() * b;

	cv::Mat result = cv::Mat::zeros(cv::Size(1, 3), CV_64FC1);
	cv::solve(c, d, result);
	std::cout << "A = " << A << std::endl;
	std::cout << "b = " << b << std::endl;
	std::cout << "result = " << result << std::endl;
	double a0 = result.at<double>(0, 0);
	double a1 = result.at<double>(1, 0);
	double a2 = result.at<double>(2, 0);
	std::cout << "对称轴：" << -a1 / a2 / 2 << std::endl;
	std::cout << "拟合方程：" << a0 << " + (" << a1 << "x) + (" << a2 << "x^2)";
	return 0;
}
int main()
{
	double a[] = { -10.,  -9.,  -8.,  -7.,  -6.,  -5.,  -4.,  -3.,  -2.,  -1.,   0.,
		 1.,   2.,   3.,   4.,   5.,   6.,   7.,   8.,   9. };
	double b[] = { 0.890928, 0.904723, 0.921421, 0.935007, 0.94281 , 0.949828,
		   0.966265, 0.975411, 0.978693, 0.97662 , 0.974468, 0.967101,
		   0.957691, 0.958369, 0.949841, 0.932791, 0.9213  , 0.901874,
		   0.879374, 0.868257 };
	std::vector<double> x;
	std::vector<double> y;
	for (int i = 0; i < (sizeof(a) / sizeof(a[0])); i++)
	{
		x.push_back(a[i]);
		y.push_back(b[i]);
	}

	fitCurve(x, y);
	return 0;
}

• 输出：

A = [1, -10, 100;
 1, -9, 81;
 1, -8, 64;
 1, -7, 49;
 1, -6, 36;
 1, -5, 25;
 1, -4, 16;
 1, -3, 9;
 1, -2, 4;
 1, -1, 1;
 1, 0, 0;
 1, 1, 1;
 1, 2, 4;
 1, 3, 9;
 1, 4, 16;
 1, 5, 25;
 1, 6, 36;
 1, 7, 49;
 1, 8, 64;
 1, 9, 81]
b = [0.8909280000000001;
 0.9047230000000001;
 0.921421;
 0.935007;
 0.94281;
 0.949828;
 0.966265;
 0.975411;
 0.978693;
 0.97662;
 0.974468;
 0.967101;
 0.957691;
 0.958369;
 0.949841;
 0.932791;
 0.9213;
 0.901874;
 0.879374;
 0.8682569999999999]
result = [0.9730115624060149;
 -0.002311438482570065;
 -0.001090408407382091]
对称轴：-1.0599
拟合方程：0.973012 + (-0.00231144x) + (-0.00109041x^2)

可以和python实现版对照着看最后拟合的方程是一样的！完美！

参考：
超定方程理论参考：https://blog.csdn.net/u014652390/article/details/52789591