机器学习:sklearn中K最近邻算法
K最近邻算法
使用的直接是sklearn中的KNN。
K最近邻算法属于监督学习的一种。
它既可以应用于分类,也可以应用于回归。
一:K最近邻算法原理
| KNN用于分类 | KNN用于回归 |
|---|---|
| 其思想是如果一个样本在特征空间中的k个最相邻的样本中的大多数属于某一个类别,则该样本也属于这个类别,并具有这个类别上样本的特性。在scikit-learn中,K最近邻算法的K值是通过n_neighbors参数来调节的,默认值是5。 | 当我们使用KNN计算某个数据点的预测值时,模型会选择距离该数据点最近的若干个训练数据集中的点,并且将他们的y值取平均值,作为新数据点的预测值。 |
二: K最近邻算法在分类中的应用
这里使用的是scikit-learn中的玩具数据集。
代码如下
# coding=gbk
import matplotlib as mpl
import matplotlib.pyplot as plt;
import numpy as np;
from sklearn.neighbors.classification import KNeighborsClassifier
from sklearn.datasets import make_blobs;
#导入KNN分类器
from sklearn.neighbors import KNeighborsClassifier
#导入数据集拆分工具
from sklearn.model_selection import train_test_split;
#-----------------------------------------------------------------
def make_datas():
#生成样本数为200 分类为2的数据集
data=make_blobs(n_samples=200, centers=2,random_state=8);
X,y=data;
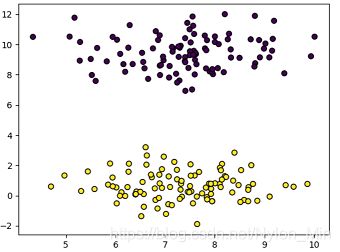
#将生成的数据集将进行可视化:
plt.scatter(X[:,0],X[:,1],c=y,edgecolors='k'); # ,cmap=plt.cm.spring
plt.show()
return X,y;
#-----------------------------------------------------------------
X,y=make_datas();
#直接调用库中间的K最近邻分类器
clf=KNeighborsClassifier();
#进行训练
clf.fit(X, y);
#-----------------------------------------------------------------
#下面的代码用于画图:
x_min,x_max=X[:,0].min()-1,X[:,0].max()+1;
y_min,y_max=X[:,1].min()-1,X[:,1].max()+1;
#取点 基本上就是x轴和y轴的点
xx,yy=np.meshgrid(np.arange(x_min,x_max,.02),np.arange(y_min,y_max,.02));
Z=clf.predict(np.c_[xx.ravel(),yy.ravel()])
#print(Z.shape) 306460,
#print(xx.shape)
Z=Z.reshape(xx.shape);
#print(Z.shape) 796,385
plt.pcolormesh(xx,yy,Z,cmap=plt.get_cmap('GnBu'));
plt.scatter(X[:,0],X[:,1],c=y,cmap=plt.get_cmap('spring'),edgecolors='k');
plt.xlim(xx.min(),xx.max());
plt.ylim(yy.min(),yy.max());
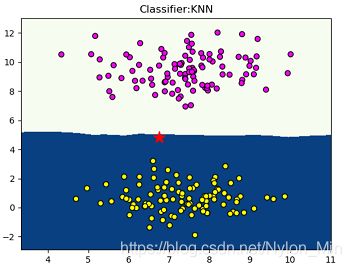
plt.title("Classifier:KNN");
plt.scatter(6.75,4.82,marker='*',c='red',s=200)
plt.show()
#-----------------------------------------------------------------
#对新的数据点进行判断
print("----------------------------------------------------------------------");
print("代码运行结果");
print("新数据的分类是:",clf.predict([[6.75,4.82]]));
print("----------------------------------------------------------------------");
print("代码运行结果");
print("新数据的分类是:",clf.predict([[6.75,8.00]]));
KNN在多分类问题中的应用
接下来,我们要先生成多元分类任务所使用的数据集,然后通过修改make_blobs的centers参数,把数据类型的数量增加到5个;修改n_samples参数,把样本量增加到500个
代码如下:
#coding=gbk;
import matplotlib as mpl
import matplotlib.pyplot as plt;
import numpy as np;
from sklearn.neighbors.classification import KNeighborsClassifier #直接导入K最近邻分类器
from sklearn.datasets import make_blobs; #导入制作数据的库
#-----------------------------------------------------------------
def makeDatas():
#生成样本数为500,分类数为5的数据集
data=make_blobs(n_samples=300,centers=5,random_state=8);
#X指的是生成的数据集中的特征值 y指的是数据集中的标记
X2,y2=data;
return X2,y2;
#-----------------------------------------------------------------
def showRawData(X2,y2):
#下面scatter中参数c指的是一个色彩或者颜色的序列
plt.scatter(X[:,0],X[:,1],c=y,cmap=plt.get_cmap("hot"),edgecolor='k');
plt.show()
#-----------------------------------------------------------------
X,y=makeDatas();
#用散点图将数据进行可视化
showRawData(X, y);
clf=KNeighborsClassifier();
clf.fit(X, y);
#-----------------------------------------------------------------
#下面用来画分类图
x_min,x_max=X[:,0].min()-1,X[:,0].max()+1;
y_min,y_max=X[:,1].min()-1,X[:,1].max()+1;
xx,yy=np.meshgrid(np.arange(x_min,x_max,.02),np.arange(y_min,y_max,.02))
Z=clf.predict(np.c_[xx.ravel(),yy.ravel()]);
Z=Z.reshape(xx.shape);
plt.pcolormesh(xx,yy,Z,cmap=plt.get_cmap('plasma'));
plt.scatter(X[:,0],X[:,1],c=y,cmap=plt.get_cmap("hot"),edgecolor='k');
plt.xlim(xx.min(),xx.max())
plt.ylim(yy.min(),yy.max())
plt.show()
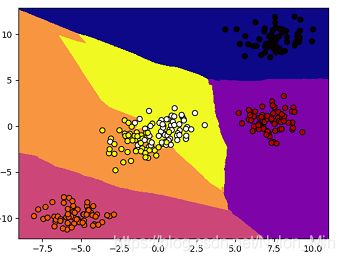
运行结果:
KNN在分类问题之中的应用,小结:
- 经过阅读上面的两个代码,其实可以发现,无论是分成了2类或是5类,我们使用sklearn中的KNN的步骤都是一样的。
-
xx,yy=np.meshgrid(np.arange(x_min,x_max,.02),np.arange(y_min,y_max,.02))
这一行可能有一些难以理解。请参照 np.meshgrid()理解
三: K最近邻算法在回归分析中的应用
在scikit-learn的数据集生成器中,有一个非常好的用于回归分析的数据集生成器make_regression函数,这里我们就使用它来生成make_regression生成数据集来进行实验。
代码如下:
#coding=gbk;
import matplotlib.pyplot as plt;
import numpy as np;
#导入make_regression数据集生成器
from sklearn.datasets import make_regression;
#导入用于回归分析的KNN模型
from sklearn.neighbors import KNeighborsRegressor;
#-----------------------------------------------------------------
#生成特征数量为1,噪音为50的数据集
X,y=make_regression(n_features=1,n_informative=1,noise=50,random_state=8);
plt.scatter(X,y,c="orange",edgecolor="k");
#plt.show(); #从图中可以看到 x的范围是(-3,3);
#-----------------------------------------------------------------
#把预测的结果用图像来进行可视化
reg=KNeighborsRegressor();
reg.fit(X,y);
z=np.linspace(-3,3,200).reshape(-1,1);
plt.plot(z,reg.predict(z),c="k",linewidth=2);
plt.title("KNN Regressor");
plt.show()
print("**************************")
print("模型评分为:{t:.3f}".format(t=reg.score(X,y)))
print("**************************")
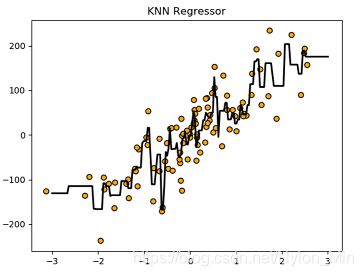
运行结果:
初始时候数据显示为(代码我注释掉了)
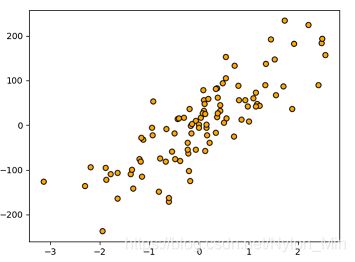
经过KNN回归:
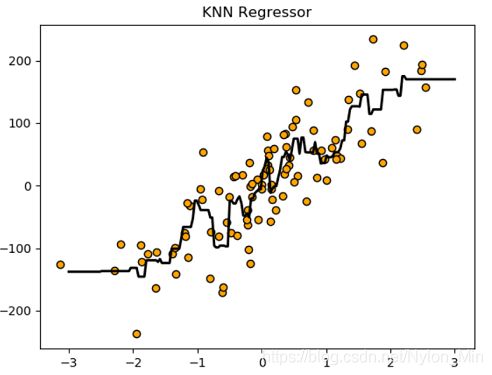
console处输出为:

又在此文的开始说过,KNN之中的K是可以通过修改参数n_neighbors的值来改变的。默认的话,n_neighbors为5。如果我们将它改成2,甚至是1会是怎么样的效果呢?
reg=KNeighborsRegressor(n_neighbors=2);
reg.fit(X,y);
此时n_neighbots=2,图为:
reg=KNeighborsRegressor(n_neighbors=1);
reg.fit(X,y);
此时n_neighbots=1,图为:
KNN在回归问题之中的应用,小结:
- 通过改变n_neighbors,从一开始的5,到后面的2,再到1。我们可以在图像中看到,线条越来越贴近更多的训练集中的点,并且模型评分也是在不断增大(注意:这里使用训练集评的分)
n_neighbors等于1的时候,模型评分竟然达到了1.000,并且线条几乎通过了所有的节点。但是很显然,这样的话肯定是过拟合了。
四: K最近邻算法实战-酒的分类:
使用scikit-learn内置的酒数据集来进行实验:
代码如下:
#coding=gbk;
import matplotlib.pyplot as plt;
import numpy as np;
from sklearn.neighbors import KNeighborsClassifier;
#将酒的数据集载入到项目之中 sklearn自带的数据集
from sklearn.datasets import load_wine;
#导入数据集拆分工具 主要就是拆出来一部分的测试集
from sklearn.model_selection import train_test_split;
from pandas.core.common import random_state
#-----------------------------------------------------------------
wineDataset=load_wine();
X_train,X_test,y_train,y_test=\
train_test_split(wineDataset['data'],wineDataset['target'],random_state=0);
#-----------------------------------------------------------------
print("********************************************");
print("数据集中的键值为{t}".format(t=wineDataset.keys()))
print("X_train的大小为:{t}".format(t=X_train.shape))
print("y_train的大小为:{t}".format(t=y_train.shape))
print("X_test的大小为:{t}".format(t=X_test.shape))
print("y_test的大小为:{t}".format(t=y_test.shape))
knn=KNeighborsClassifier(n_neighbors=2);
knn.fit(X_train,y_train);
print("测试集的得分为:{t}".format(t=knn.score(X_test,y_test)));
print("********************************************")
#-----------------------------------------------------------------
#输入新的数据点:
X_new=np.array([[13.2,2.77,2.51,18.5,96.6,1.04,2.55,0.57,1.47,6.2,1.05,3.33,820]])
prediction=knn.predict(X_new);
print("预测这种酒的分类为:{}".format(wineDataset["target_names"][prediction]));
酒,小结:
- 如果对train_test_split()函数之中的random_state参数不理解,请参考random_state的理解
- 并且可以自己通过尝试,random_state取不同的值,最后获得的测试集的得分也不一样。
总结:
K最近邻算法在实际使用当中会有很多问题,例如它需要对数据集认真地进行预处理,对规模超大的数据集拟合的时间较长,对高维数据集拟合欠佳,以及对于稀疏数据集束手无策等
遇事不决,可问春风。