03_01 python机器学习_第三章无监督学习与预处理
第三章无监督学习与预处理
第二章监督学习中介绍了不少训练模型,这些模型都需要喂数据,调试参数以达到预想结果,
由于模型理解相对较复杂,因此使用独立章节学习总结.
而第三章内容衔接比较紧凑因此合并学习.
第二章内容属于监督学习部分,都需要人工参与分析选择模型.
第三章内容属于无监督学习部分,核心是围绕着如何自动分析数据展开.
第三章共分3大部分
- 数据缩放(属于通用的数据处理方式)
第二章在学习线性模型的时候有接触过,主要是讲解如何将差异很大的数据特征都调校到同一水平.
这部分的内容可以同时应用在训练及测试数据上. - 数据变换(解构数据)
主要内容讲解如何降低数据纬度,如何提取数据成分,如何将高维数据可视化.
用于算法的独特性,这部分内容只能应用在训练数据上. - 数据凝聚(聚类)
(2)在提取数据的过程会删掉不重要的数据特征,而(3)会保留数据特征
主要内容是如何将数据按分类分组(簇).
同样的这部分的算法也这能用在训练数据之上.
开始学习之前,我们在脑海里先回顾一下第二章学习的那些模型,
都是一个通用模式: 类实例化 -> fit(训练数据) -> transform(训练数据/测试数据)
通俗来说就是构建模型,配置调校模型,应用模型.
书上给出一种官方的说法:
这些模型统一称作:估计器(estimator)
- 所有的估计器中都包含算法,同时也保存了利用算法从数据中学到的模型.
- 都有的估计器都有fit方法, 第一参数永远是x数据(NumPy 数组或SciPy 稀疏矩阵)
每一行代表一个数据点. 还需要一个目标参数y, - 应用模型主要有两种方法:
- 想要创建一个新的y, 比如predict
- 想要创建一个新的x的表示 比如transform
- 所有的模型都有source(x,y),可以评估模型.
01 无监督学习的类型
- 变换(dimensionality reduction)
降维数据,从复杂数据中筛选出数据的主要部分 - 聚类(clustering algorithm)
按照某些相似特征将数据进行分组
02 数据预处理 数据缩放
以直观的方式观察缩放后的数据表现.
# 数据预处理_数据缩放种类快速演示
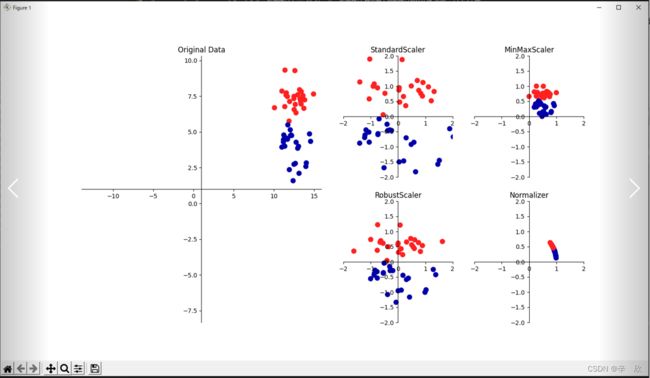
# 1. 左图为原始数据样本 数据范围 X: 0~15, Y: 0~10.
# 2. 右图4张为缩放后样本
# 1. 上左(StandardScaler): 每个特征的平均值为0,方差调整为1.由于强调的是整体,因此对于最大最小值可能不会太友好.
# 2. 上右(MinMaxScaler): 将特征都移动到X,Y都是0~1的矩阵范围内(想象一下离远点看数据,或将XY轴的测量单位扩大几倍).
# 3. 下左(RobustSclaer): 跟1差不多, 但是它用的是 中位数或四分位数.
# 4. 下右(Normalizer): 调整欧式长度为1(想象一下半径为1的球体)
# 中位数: 指有那么一个数可以让整体的数据一半比它大一半比它小.
# 四分位数: 跟中位数类似, 不过它不是一半而是1/4.
import mglearn
import matplotlib.pyplot as plt
mglearn.plots.plot_scaling()
plt.show()
02_01 MinMaxScaler缩放原理
函数帮助中介绍的原理:
X_std = (X - X.min(axis=0)) / (X.max(axis=0) - X.min(axis=0))
X_scaled = X_std * (max - min) + min
# 数据预处理_MinMaxScaler缩放原理
# 数据样本源
from re import M
from sklearn.datasets import load_breast_cancer
# 数据拆分
from sklearn.model_selection import train_test_split
# 用于将数据缩放到 X,Y 为1的矩阵中
from sklearn.preprocessing import MinMaxScaler
# 数据准备
cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(
cancer.data, cancer.target, random_state=1)
# 缩放类准备
# 原理:
# The transformation is given by::
# X_std = (X - X.min(axis=0)) / (X.max(axis=0) - X.min(axis=0))
# X_scaled = X_std * (max - min) + min
scaler = MinMaxScaler()
# 不同与模型的fit函数, 缩放函数之填充训练数据就行.
# 因为缩放只关心源,不关心目标类别
scaler.fit(X_train)
# 这个有点奇怪,直接实例化然后变换就行了呗,为啥中间还要喂一遍数据?
# 看函数帮助也是这么用的.
# fit函数可能的作用是先预读数据样本,确定样本中一些内容,不如个数,最大,最小值等等,
# 以此来确定数据的轮廓,在转换时会参照这个轮廓来变换数据.理论上喂的数据不用跟变换数据必须一致.
X_train_scaler = scaler.transform(X_train)
# 缩放不会改变结构,只会改变大小
# In [19]: X_train_scaler.shape
# Out[19]: (426, 30)
# In [20]: X_train.shape
# Out[20]: (426, 30)
# In [41]: X_train.min(axis=0)
# Out[41]:
# array([6.981e+00, 9.710e+00, 4.379e+01, 1.435e+02, 5.263e-02, 1.938e-02,
# 0.000e+00, 0.000e+00, 1.060e-01, 5.024e-02, 1.153e-01, 3.602e-01,
# 7.570e-01, 6.802e+00, 1.713e-03, 2.252e-03, 0.000e+00, 0.000e+00,
# 9.539e-03, 8.948e-04, 7.930e+00, 1.202e+01, 5.041e+01, 1.852e+02,
# 7.117e-02, 2.729e-02, 0.000e+00, 0.000e+00, 1.566e-01, 5.521e-02])
# In [42]: X_train_scaler.min(axis=0)
# Out[42]:
# array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
# 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])
# In [43]: X_train.max(axis=0)
# Out[43]:
# array([2.811e+01, 3.928e+01, 1.885e+02, 2.501e+03, 1.634e-01, 2.867e-01,
# 4.268e-01, 2.012e-01, 3.040e-01, 9.575e-02, 2.873e+00, 4.885e+00,
# 2.198e+01, 5.422e+02, 3.113e-02, 1.354e-01, 3.960e-01, 5.279e-02,
# 6.146e-02, 2.984e-02, 3.604e+01, 4.954e+01, 2.512e+02, 4.254e+03,
# 2.226e-01, 9.379e-01, 1.170e+00, 2.910e-01, 5.774e-01, 1.486e-01])
# In [44]: X_train_scaler.max(axis=0)
# Out[44]:
# array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
# 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.])
X_test_scaler = scaler.transform(X_test)
# 对于测试数据达不到完全缩放. 结果可以看出有的小于0,大于1,不如训练数据缩放的结果完美.
# In [46]: X_test_scaler.min(axis=0)
# Out[46]:
# array([ 0.0336031 , 0.0226581 , 0.03144219, 0.01141039, 0.14128374,
# 0.04406704, 0. , 0. , 0.1540404 , -0.00615249,
# -0.00137796, 0.00594501, 0.00430665, 0.00079567, 0.03919502,
# 0.0112206 , 0. , 0. , -0.03191387, 0.00664013,
# 0.02660975, 0.05810235, 0.02031974, 0.00943767, 0.1094235 ,
# 0.02637792, 0. , 0. , -0.00023764, -0.00182032])
# In [47]: X_test_scaler.max(axis=0)
# Out[47]:
# array([0.9578778 , 0.81501522, 0.95577362, 0.89353128, 0.81132075,
# 1.21958701, 0.87956888, 0.9333996 , 0.93232323, 1.0371347 ,
# 0.42669616, 0.49765736, 0.44117231, 0.28371044, 0.48703131,
# 0.73863671, 0.76717172, 0.62928585, 1.33685792, 0.39057253,
# 0.89612238, 0.79317697, 0.84859804, 0.74488793, 0.9154725 ,
# 1.13188961, 1.07008547, 0.92371134, 1.20532319, 1.63068851])
02_02 MinMaxScaler缩放前后对比
# 数据预处理_MinMaxScaler缩放前后对比
import mglearn
import matplotlib.pyplot as plt
# 生成聚类数据
from sklearn.datasets import make_blobs
from sklearn.model_selection import train_test_split
# 缩放类
from sklearn.preprocessing import MinMaxScaler
# 讲解数据缩放并不关心种类目标,因此没有y
# make_blobs 用于生成聚类数据
# n_samples 创建的样本个数
# centers 目标种类个数 本例将生成5各类别的数据
# random_state 随机种子用于打乱数据
# cluster_std 标准偏差 默认是1
X, _ = make_blobs(n_samples=50, centers=5, random_state=4, cluster_std=2)
X_train, X_test = train_test_split(X, random_state=5, test_size=.1)
#######################
# 第一个画布,使用原始数据绘制散点图
#######################
# 绘制训练集和测试集
fig, axes = plt.subplots(1, 3, figsize=(13, 4))
axes[0].scatter(X_train[:, 0], X_train[:, 1],
c=mglearn.cm2(0), label="Training set", s=60)
axes[0].scatter(X_test[:, 0], X_test[:, 1], marker='^',
c=mglearn.cm2(1), label="Test set", s=60)
axes[0].legend(loc='upper left')
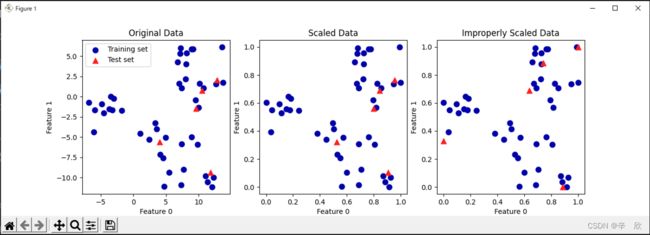
axes[0].set_title("Original Data")
#######################
# 第二个画布,同时缩放训练数据和测试数据
#######################
# 因为使用了同时缩放,因此即使标尺改变也不影响预测结果
# 从图中可以看出,散点图与原始图接近
# 利用MinMaxScaler缩放数据
scaler = MinMaxScaler()
# 缩放都是先fit在transform,其实有个方法是fit_transform可以整合这俩个方法,而且运行效率较高
# 例如: scaler.fit_transform(X_train) 来简化步骤
scaler.fit(X_train)
X_train_scaled = scaler.transform(X_train)
X_test_scaled = scaler.transform(X_test)
# 将正确缩放的数据可视化
axes[1].scatter(X_train_scaled[:, 0], X_train_scaled[:, 1],
c=mglearn.cm2(0), label="Training set", s=60)
axes[1].scatter(X_test_scaled[:, 0], X_test_scaled[:, 1], marker='^',
c=mglearn.cm2(1), label="Test set", s=60)
axes[1].set_title("Scaled Data")
#######################
# 第三个画布,只对测试数据进行缩放
#######################
# 要么就全缩放,要么就全不缩放,只缩放一部分相当于改变了衡量标准,
# 因此模型会认为其中一部分数据有重大偏差进而影响预测结果.
test_scaler = MinMaxScaler()
test_scaler.fit(X_test)
X_test_scaled_badly = test_scaler.transform(X_test)
# 将错误缩放的数据可视化
axes[2].scatter(X_train_scaled[:, 0], X_train_scaled[:, 1],
c=mglearn.cm2(0), label="training set", s=60)
axes[2].scatter(X_test_scaled_badly[:, 0], X_test_scaled_badly[:, 1],
marker='^', c=mglearn.cm2(1), label="test set", s=60)
axes[2].set_title("Improperly Scaled Data")
for ax in axes:
ax.set_xlabel("Feature 0")
ax.set_ylabel("Feature 1")
plt.show()
02_03 数据缩放对模型的影响
为了便于较明显的说明效果,我们使用对缩放比较敏感的核支持向量机模型来进行实验.
# 数据变换_缩放对模型的影响
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_breast_cancer
from sklearn.svm import SVC
# 将数据缩放到 x,y为1的矩阵中
from sklearn.preprocessing import MinMaxScaler
# 特征平均为0, 方差为1
from sklearn.preprocessing import StandardScaler
# 数据准备
cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target,
random_state=0)
svm = SVC(C=100)
svm.fit(X_train, y_train)
print("Test set accuracy: {:.2f}".format(svm.score(X_test, y_test)))
# Test set accuracy: 0.94
#########################
# 使用MinMaxScaler缩放模型
#########################
scaler = MinMaxScaler()
scaler.fit(X_train)
X_train_scaled = scaler.transform(X_train)
X_test_scaled = scaler.transform(X_test)
svm.fit(X_train_scaled, y_train)
print("Scaled test set accuracy: {:.2f}".format(
svm.score(X_test_scaled, y_test)))
# Scaled test set accuracy: 0.97
#########################
# 使用StandardScaler缩放模型
#########################
scaler = StandardScaler()
scaler.fit(X_train)
X_train_scaled = scaler.transform(X_train)
X_test_scaled = scaler.transform(X_test)
# 在缩放后的训练数据上学习SVM
svm.fit(X_train_scaled, y_train)
# 在缩放后的测试集上计算分数
print("SVM test accuracy: {:.2f}".format(svm.score(X_test_scaled, y_test)))
# SVM test accuracy: 0.96
03 数据变换_主成分分析PCA
变换数据的一种方式: PCA(principal components analysis)
特点:
- PCA重在找出主要成分
- PCA不关心数据方向
- PCA可以自己降维数据提取主成分
- 越重要的成分排名越靠前
结合以上特点,我觉的PCA适合模糊匹配(因为不关心方向,因此有偏移没关系),并且能找到最像的结果.
顺便说一下,书中的例子是用PCA来找人脸.
为了好理解,举个例子:
训练数据使用人脸正面靠镜框左面的图片,测试数据使用靠右面的图片,PCA就能很容易的识别出来.
# 数据变换_PCA 特征提取快速演示
# 特征提取的代码虽然很少但是信息量很大
# 特征提取用的最多的就是 主成分分析(principal component analysis 简称PCA)
# PCA算法的步骤是:
# 1. 寻找主要数据,标记主数据的方向.
# 同过计算方差,找到方差最大的方向,将其标记成主数据.
# 主数据的方向应当是包含数据最多且特征之间最为相关.
# 2. 沿着主数据的垂直方向寻找信息最多的方向.
# 二维空间对于x轴的垂直方向就是y轴,但是在空间上与x轴垂直的方向可是有很多.
# 模型负责在这些方向上找出信息最多的那个.
# 3. 旋转主数据方向,使主数据与x轴重合
# 我猜测模型的预测计算等都是使用标准化的z轴为基础的,因此需要将数据像标准化.
# 找到主数据方向后,整体旋转数据,使主数据方向平行与x轴重合.
# 重合后的主数据,其平局值可能与x轴平行也可能与X轴重合,为了不影响模型判断因此先减去这部分平均值
# 最终得到右上图的效果,主数据方向延x轴延申,且全部以0(Y轴)为中心.
# 4. 降维
# 仅保留一部分主数据,去掉其它非主要数据来达到降维的目的.
# 得到坐下图中一条直线. (是不是线性模型就是这么找方向的呢?)
# 5. 还原数据方向
# 再次旋转数据,使整理后的数据方向与元数据主数据的方向一致.
# 将第三步中临时去掉的平均值再加回来,保持主数据的完整性.最终得到右下图
# 以上使PCA算法的思路,虽然会损失一部分的数据特征(噪点),但是可以找到真正有用的主数据方向
# 需要注意的是主数据不是主特征.主数据表示最能代表数据含义的一组或多组数据特征集合.
import mglearn
from matplotlib import pyplot as plt
mglearn.plots.plot_pca_illustration()
plt.show()
03_01 不使用数据缩放的多特征数据如何表示
首先多特征数据不能用散点图来表示,不是实现不了而是实现了无法直观的看到结果.
例如肿瘤数据,特征数多大30个,将这些点绘制在同一个图上没什么可读性.
在为应用PCA之前,有一种折中解决方案,虽然也很乱,但是至少具备了可读性.
肿瘤数据虽然特征数众多,但是类别只有良性跟恶性两种.
因此可以画出每一个特征的良性和恶性结果,图像表示上选用直方图(较散点图直观),
查找重合部分最少的那个特征(重合少代表类别区分明显),即为PCA中的主成分.
# 数据变换_多特征&无缩放如何表示
import mglearn
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
fig, axes = plt.subplots(15, 2, figsize=(10, 20))
malignant = cancer.data[cancer.target == 0]
benign = cancer.data[cancer.target == 1]
# 将绘图结构变成线性结构
ax = axes.ravel()
for i in range(30):
# histogram 在numpy下用于表示数据的直方图
# 函数帮助参照: https://www.cjavapy.com/article/1103/
# 其它的参数函数说明介绍的很清楚了,这里单独讲一下bins参数
# bins: 直方图中柱状图的个数
# 有三种入力模式, 数字,序列,字符串.这里只讲前两种
# 数字: 柱状图个数,首先会取得数组集合中的虽大值最小值作为边界,然后通过linspace来自动填充
# 使得均匀分布的柱状个数=bins值
# 序列: 跟上面的差不多,区别在于柱状图的范围完全由序列指定.
# 例子(数字):
# bin为数字时,个数小于类别个数的时候,会在最小,最大范围内,自己寻找均等位置
#
# In [21]: np.histogram([1, 2, 1], bins=1)
# Out[21]: (array([3], dtype=int64), array([1., 2.]))
#
# In [23]: np.histogram([1, 2, 1,8], bins=2)
# Out[23]: (array([3, 1], dtype=int64), array([1. , 4.5, 8. ]))
#
# bin的值在histogram中计算时是 bin+1.
# In [50]: np.linspace(1,8, 3)
# Out[50]: array([1. , 4.5, 8. ])
# 例子(序列):
# In [46]: np.histogram([1, 2, 1,8,4], bins=[2,3,6,8])
# Out[46]: (array([1, 1, 1], dtype=int64), array([2, 3, 6, 8]))
# 因为指定了返回值范围,因此只能返回范围内找到的值
# 范围2~3, 找到2, 返回个数1
# 范围3~6, 找到4, 返回个数1
# 范围6~8, 找到8, 返回个数1
# 因此返回的是array([1, 1, 1]
# 把范围最小值1设置上,看看结果
# In [51]: np.histogram([1, 2, 1,8,4], bins=[1,2,3,6,8])
# Out[51]: (array([2, 1, 1, 1], dtype=int64), array([1, 2, 3, 6, 8]))
# 这个值已经能够看懂了吧.
# 通过上面的介绍,基本了解了函数是做什么用的,接下来会到这个例子
# 这个函数的第一个返回值是 概率或者个数对接下来的画图没有用因此用"_"占位,直接舍弃
# 第二个参数返回的是柱状图每个柱的范围,是画图中需要用到的.
_, bins = np.histogram(cancer.data[:, i], bins=50)
# 上面np中的hitogram是为了造柱子的轮廓数据,绘图类ax中的hist是实际的画图
# 分别用良性/恶性样本中的每个特征数据来画柱状图
ax[i].hist(malignant[:, i], bins=bins, color=mglearn.cm3(0), alpha=.5)
ax[i].hist(benign[:, i], bins=bins, color=mglearn.cm3(2), alpha=.5)
ax[i].set_title(cancer.feature_names[i])
ax[i].set_yticks(())
ax[0].set_xlabel("Feature magnitude")
ax[0].set_ylabel("Frequency")
ax[0].legend(["malignant", "benign"], loc="best")
# 紧凑显示画布上的绘图
fig.tight_layout()
plt.show()
 上图中,柱状图交集越少,边界越清晰,越容易判断分类.比如: 结果中的"worst concave points”.
上图中,柱状图交集越少,边界越清晰,越容易判断分类.比如: 结果中的"worst concave points”.
03_02 使用PCA表示多特征数据
# 数据变换_PCA 分析多特征
import mglearn
import matplotlib.pyplot as plt
# 主成分分析库
from sklearn.decomposition import PCA
from sklearn.datasets import load_breast_cancer
from sklearn.preprocessing import StandardScaler
#####################
# 准备数据,并进行数据的缩放
#####################
cancer = load_breast_cancer()
scaler = StandardScaler()
scaler.fit(cancer.data)
X_scaled = scaler.transform(cancer.data)
#####################
# 实例化PCA,指定保留2个重要主成分
#####################
# 跟快速演示中的不太一样,看样子PCA只是用于提取,并没有缩放功能,缩放需要自己单独写
pca = PCA(n_components=2)
# 初始化数据分析轮廓
pca.fit(X_scaled)
# compents_ 属性中存放有序主成分,越重要的主成分越靠前
# In [4]: pca.components_.shape
# Out[4]: (2, 30)
# 提取主成分
X_pca = pca.transform(X_scaled)
print("Original shape: {}".format(str(X_scaled.shape)))
print("Reduced shape: {}".format(str(X_pca.shape)))
# Original shape: (569, 30)
# Reduced shape: (569, 2)
# 成功提取出来俩个特征
#####################
# 画图 主成分的散点图
#####################
plt.figure(figsize=(8, 8))
mglearn.discrete_scatter(X_pca[:, 0], X_pca[:, 1], cancer.target)
plt.legend(cancer.target_names, loc="best")
plt.gca().set_aspect("equal")
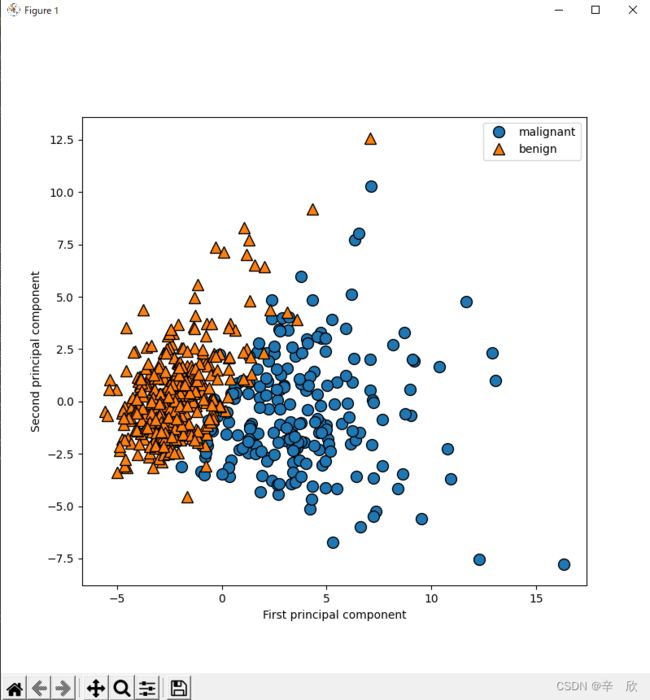
plt.xlabel("First principal component")
plt.ylabel("Second principal component")
plt.show()
在这个图上分析结果就容易的多了.决策边界肉眼也能看出来.说明提取的还是很准确的.
这个是比较让人直观感受到的好处,其中的另一个好处才是这个算法的精妙之处.
提取主成分时,咱们并没有指明使用哪个特征,完全时模型自主判断出来的,
这对于今后的自动化分析处理数据有很重要的意义.
03_03 使用PCA处理人脸数据
现在不少应用都有人脸识别,在首次录入人脸数据的时候最多也就4张图, 正面,侧面,张嘴,眨眼等.
从之前的学习模型中我们可以知道,训练数据越少,模型越可能欠拟合.
而且,我们每次识别人脸的时候并不是正好能与录制时的位置重合,对于像素数据来说差一点可能偏差很大,
因此,即使是训练得分很高的模型也有可能出现匹配失败.
但是我们实际体验来看,各应用的人脸识别度匹配度很高,这个是怎么做到的呢?
PCA登场,人脸数据在采集的时候,特征数据会非常多. PCA会从其中抽取主要特征用作分析,
又因为PCA的特点,对数据的位置不敏感,也就对测试数据的偏移不敏感,因此很适合人脸数据的比对.
# 数据变换_PCA 提取特征脸
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_lfw_people
from sklearn.model_selection import train_test_split
from sklearn.decomposition import PCA
# min_faces_per_person=20 每人最少20张人脸图片
people = fetch_lfw_people(min_faces_per_person=20, resize=0.7)
image_shape = people.images[0].shape
##################
# 第一画布 显示人脸图像
##################
fix, axes = plt.subplots(2, 5, figsize=(15, 8),
subplot_kw={'xticks': (), 'yticks': ()})
for target, image, ax in zip(people.target, people.images, axes.ravel()):
ax.imshow(image)
ax.set_title(people.target_names[target])
##################
# 处理人脸图像
##################
# 每人人脸图像采样最多50个
mask = np.zeros(people.target.shape, dtype=np.bool)
for target in np.unique(people.target):
# np.where(condition) 这个是numpy中的方法不能直接作用在list上
# a = np.array([1,2,3,4])
# 通过np.array做成的都是高维数组,即使只有1维数据也表示成(xx,)的形式
# a.shape -> (4,)
# 取得满足条件的数据的位置
# np.where(a > 2) -> (array([2, 3], dtype=int64),)
# 应当用这种方式取得一维的数据
# np.where(a > 2)[0] -> array([2, 3], dtype=int64)
# 通过上面的例子分析一下np.where(people.target == target)[0][:50]
# 1.np.where(people.target == target)[0] 就是直接找到匹配条件的数据位置
# 2.[:50] 满足条件的同一结果的所有位置数据中只要前50个位置
# 3.mask[XXX] = 1 将符合条件的前50个位置标记成True,用于以后的取数据
mask[np.where(people.target == target)[0][:50]] = 1
X_people = people.data[mask]
y_people = people.target[mask]
##################
# 第二画布 使用PCA抽取主成分成像
##################
# stratify 以指定参数的成分比例拆分数据
X_train, X_test, y_train, y_test = train_test_split(
X_people, y_people, stratify=y_people, random_state=0)
# 抽取前100主要成分
# whiten: 白化处理,可以将主成分缩放到相同的比例
pca = PCA(n_components=100, whiten=True, random_state=0).fit(X_train)
fix, axes = plt.subplots(3, 5, figsize=(15, 12), subplot_kw={
'xticks': (), 'yticks': ()})
# 将主成分成像
# zip函数可以将两个数组通过位置1对1匹配,凑不成1对时,停止
# In [73]: list(zip([3,2], [1,2,3]))
# Out[73]: [(3, 1), (2, 2)]
for i, (component, ax) in enumerate(zip(pca.components_, axes.ravel())):
# 将主成分格式化成图像一致的横纵比
ax.imshow(component.reshape(image_shape), cmap='viridis')
ax.set_title("{}. component".format((i + 1)))
plt.show()
04 数据变换_非负矩阵分解 NMF
非负矩阵分解(non-negative matrix factorization,NMF)
特点:
- 跟PCA相同的是,也可以降维数据用于提取主成分,主成分越重要排名也越靠前.
- PCA是无方向的,而NMF是有方向的.
- NMF要求数据全是正数(因为是带有方向的算法,为了准确描述方向因此不能有负数,因为负数可能会抵消一部分正数,导致方向出现偏差)
- NMF可以较准确的还原数据的某种特征,但是不及PCA,因为NMF会只关心所指定的特征.
结合以上特点:
NMF的侧重是找对(PCA是找出)
还是那人脸举例,正面稍向左转头和向右稍转头对于PCA来说可能是一种,
而对于NMF就是两种.
先简单看一下NMF的快速演示以便于理解上面那段说明.
# 数据变换_NMF 快速演示
# NMP与PCA相比图要简单一些,没有PCA的旋转,去成分,再旋转等操作
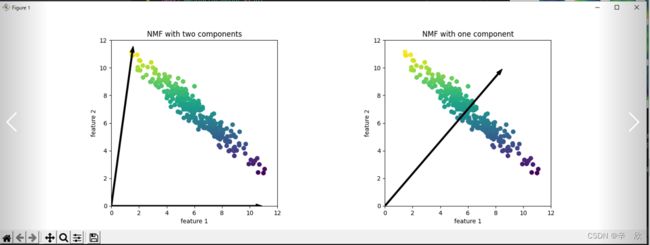
# 但是NMP很明显可以看到数据分类的方向
# 第一图是二分类数据, 两个箭头分别指向分类的方向
# 第二图是一分类数据, 箭头正好均分数据
# 要是多分类的话理论上会有多个箭头指向各个分类的方向
import mglearn
import matplotlib.pyplot as plt
mglearn.plots.plot_nmf_illustration()
plt.show()
04_01 NMF原理及应用
前提:
首先需要注意的是NMF只能作用在非负的数据集上.
原理:
书中原话: 试图将每个数据点写成一些分量的加权求和.
我是没太理解,我觉得是像描述: 试图将每个数据点都用分量+加权,通过算法来描述数据位置.
NMF是带有方向的,为了能准确描述方向,需要用正值数据来计算.负值在计算时叠加会对冲数据,影响方向准确度.
使用场合:
合成声音中准确识别各个声音, 面部数据中可以利用NMF的特点识别同一朝向人脸.
04_02 NMF分析人脸图像
# 数据变换_NMF 处理人脸数据
# 概要:
# 1.使用NMF模型降维,并提取人脸数据种重要的15种主要成分
# 2.将这15种主要成分绘图
# 3.以2种第三种主要成分抽取人脸数据并绘图 (向右)
# 4.以10种第三种主要成分抽取人脸数据并绘图 (向左)
# 通过以上例子可以看出NMF不仅可以降维提取主成分,还可以汇集方向一致的数据
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import NMF
from sklearn.datasets import fetch_lfw_people
from sklearn.model_selection import train_test_split
# min_faces_per_person=20 每人最少20张人脸图片
people = fetch_lfw_people(min_faces_per_person=20, resize=0.7)
image_shape = people.images[0].shape
# In[4]: image_shape
# Out[4]: (87, 65)
# stratify 以指定参数的成分比例拆分数据
X_train, X_test, y_train, y_test = train_test_split(
people.data, people.target, stratify=people.target, random_state=0)
# 创建NMF模型并填充数据
# 设定n_components, 使模型选择最重要的15种主要成分用于显示
nmf = NMF(n_components=15, random_state=0)
nmf.fit(X_train)
# 绘图
#######################
# 使用NMF像是15种主要成分 (先总览一下都找出了哪些重要成分)
#######################
fix, axes = plt.subplots(3, 5, figsize=(15, 12),
subplot_kw={'xticks': (), 'yticks': ()})
# In[3]: nmf.components_.shape
# Out[3]: (15, 5655)
for i, (component, ax) in enumerate(zip(nmf.components_, axes.ravel())):
ax.imshow(component.reshape(image_shape))
ax.set_title("{}. component".format(i))
#######################
# 使用NMF仅显示第符合第三种主要成分的人脸数据(向左)
#######################
# 先用数据转换一下原始数据
# 目的时降维和汇总主成分数据
X_train_nmf = nmf.transform(X_train)
X_test_nmf = nmf.transform(X_test)
# In[8]: X_train.shape
# Out[8]: (1658, 5655)
# In[9]: X_train_nmf.shape
# Out[9]: (1658, 15)
compn = 3
# argsort使用方法
# argsort(start_index, end_index, step)
# In[13]: a = np.array([4, 3, 5, 6])
# In[14]: np.argsort(a)
# Out[14]: array([1, 0, 2, 3], dtype=int64)
# In[15]: np.argsort(a)[:]
# Out[15]: array([1, 0, 2, 3], dtype=int64)
# In[16]: np.argsort(a)[::-1]
# Out[16]: array([3, 2, 0, 1], dtype=int64)
inds = np.argsort(X_train_nmf[:, compn])[::-1]
fig, axes = plt.subplots(2, 5, figsize=(15, 8),
subplot_kw={'xticks': (), 'yticks': ()})
for i, (ind, ax) in enumerate(zip(inds, axes.ravel())):
ax.imshow(X_train[ind].reshape(image_shape))
#######################
# 使用NMF仅显示第符合第十种主要成分的人脸数据 (向右)
#######################
compn = 10
inds = np.argsort(X_train_nmf[:, compn])[::-1]
fig, axes = plt.subplots(2, 5, figsize=(15, 8),
subplot_kw={'xticks': (), 'yticks': ()})
for i, (ind, ax) in enumerate(zip(inds, axes.ravel())):
ax.imshow(X_train[ind].reshape(image_shape))
plt.show()
04_03 PCA & NMF 处理信号
PCA和NMF都有过滤提取主成分的功能,之前演示的是人脸图形的分析,
接下尝试分析波形信号数据,看一下算法测呈现效果如何.
# 数据变换_PCA & NMF 处理信号
# 处理概要:
# 1.创建信号源
# 2.提高信号源的复杂度
# 3.使用NMF解析2的信号,取出前三个主要成分
# 4.使用PCA解析2的信号,取出前三个主要成分
# 5.将1,2,3,4分别绘图
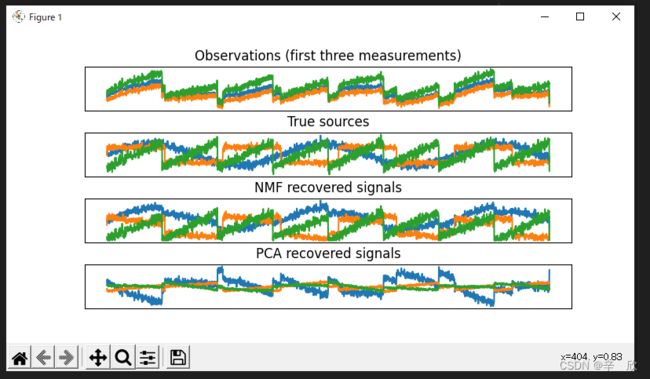
# 结论:
# step1:原始信号为3个,波形较接近,有重叠的部分
# step2:提高数组维数后,不同信号波形之间出现明显分离,较容易区分每个信号
# step3:NMF可以降维取出主要成分,并能较准确的还原step2种的信号波形
# step4:PCA也可以降维取出主要成分,但是绘制波形出现了明显的误差与step1,2的波形完全不匹配
# 尝试:
# step3: 将n_components的值设置>3, 结果相同
# step4: 将n_components的值设置>3, 结果相同
# 因此PCA,NMF在寻找主成分上还是没有问题的
# 导致step4出现误差的原因:
# PCA不关心方向,通过旋转 -> 去成分 -> 旋转 的方式寻找主要成分, 旋转一定会带来一部分的损失
# 我理解PCA就是想方设法"找出",而NMF是想法设法"找对"
# 也就是: PCA(find: "a*") NMF(find: "abc")
import numpy as np
import matplotlib.pyplot as plt
import mglearn
from sklearn.decomposition import PCA, NMF
################################
# 创建一组原始信号
################################
S = mglearn.datasets.make_signals()
# In[3]: S.shape
# Out[3]: (2000, 3)
################################
# 提高数据的维数, 就是把数据搞复杂些
################################
# RandomState(0)
# 需要提供一个随机种子用于计算, 相同的种子会得到相同的结果
# np.random.RandomState.uniform(low=0.0, high=1.0, size=None)
# In[32]: np.random.RandomState(1).uniform()
# Out[32]: 0.417022004702574
# In [44]: np.random.RandomState(0).uniform()
# Out[44]: 0.5488135039273248
# In [45]: np.random.RandomState(0).uniform()
# Out[45]: 0.5488135039273248
# size: 用于指定生成的结构
# In[13]: np.random.RandomState(0).uniform(size=(3, 100)).shape
# Out[13]: (3, 100)
# In[15]: np.random.RandomState(0).uniform(size=(100, 3)).shape
# Out[15]: (100, 3)
A = np.random.RandomState(0).uniform(size=(100, 3))
# In[2]: A.T.shape
# Out[2]: (3, 100)
# dot help: https://www.icode9.com/content-1-1198894.html
X = np.dot(S, A.T)
# In[4]: X.shape
# Out[4]: (2000, 100)
print("Shape of measurements: {}".format(X.shape))
################################
# 使用NMF还原信号
################################
nmf = NMF(n_components=3, random_state=42)
S_ = nmf.fit_transform(X)
################################
# 使用PCA还原信号
################################
pca = PCA(n_components=3)
H = pca.fit_transform(X)
################################
# 绘制上面数据的图片:
# [原始信号, 混合后高维数组的信号, NMF还原的信号, PCA还原的信号]
################################
models = [X, S, S_, H]
names = ['Observations (first three measurements)',
'True sources',
'NMF recovered signals',
'PCA recovered signals']
# hspace 控制两个绘图之间的间距(上下间隔高度)
fig, axes = plt.subplots(4, figsize=(8, 4), gridspec_kw={'hspace': .5},
subplot_kw={'xticks': (), 'yticks': ()})
for model, name, ax in zip(models, names, axes):
ax.set_title(name)
ax.plot(model[:, :3], '-')
plt.show()
05 数据变换_流形学习算法之一 t-SNE
流形学习算法(manifold learning algorithm)
这个算法的侧重是尽可能的分析训练数据,并将数据可视化.
因此比较适合原预先分析数据,然后决定使用哪种模型算法来继续下一步.
不可以用在测试数据上.
流行学算法之一的t-SNE用于可以可视化数据.
原理:
- 将可视化数据显示在一个二维空间中.
- 表示时尽量保证原始数据点之间的距离
- 为了将数据表示在二维空间中,会生成二维空间中相对于原始数据的表示
- 生成的新二维表示会是相近的点更加相近,远离的点更加远离.
总结: 降维数据表示在二维空间,运用算法使相近的点更集中.
# 数据变换_流式学习t-SNE 可视化数据
# 概要:
# 1. 创建手写数据, 表示手写图片
# 2. 使用PCA尝试区分手写数据,使用散点图查看PCA分类状况
# 3. 使用t-SNE尝试step2的内容
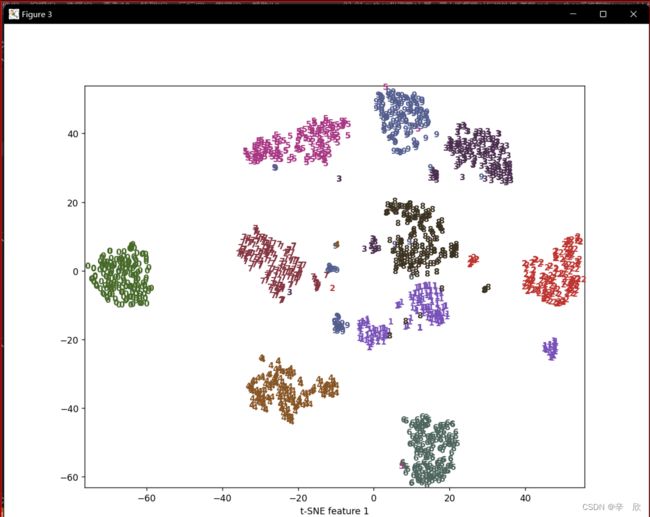
# 结论:
# PCA可以找出分类,但是各分类间的决策边界不明显,分析数据不直观
# t-SNE可以找出分类,并且会会将同类数据尽量靠近表示,决策边界明显,图像只管.
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits
from sklearn.decomposition import PCA
from sklearn.manifold import TSNE
#################
# 绘制手写数据
#################
digits = load_digits()
fig, axes = plt.subplots(2, 5, figsize=(10, 5),
subplot_kw={'xticks': (), 'yticks': ()})
for ax, img in zip(axes.ravel(), digits.images):
ax.imshow(img)
#################
# PCA分析手写数据
#################
pca = PCA(n_components=2)
pca.fit(digits.data)
digits_pca = pca.transform(digits.data)
colors = ["#476A2A", "#7851B8", "#BD3430", "#4A2D4E", "#875525",
"#A83683", "#4E655E", "#853541", "#3A3120", "#535D8E"]
plt.figure(figsize=(10, 10))
plt.xlim(digits_pca[:, 0].min(), digits_pca[:, 0].max())
plt.ylim(digits_pca[:, 1].min(), digits_pca[:, 1].max())
for i in range(len(digits.data)):
# 将数据实际绘制成文本,而不是散点
plt.text(digits_pca[i, 0], digits_pca[i, 1], str(digits.target[i]),
color=colors[digits.target[i]],
fontdict={'weight': 'bold', 'size': 9})
# 散点图 想看散点图的去掉下面注释
# plt.scatter(digits_pca[i, 0], digits_pca[i, 1])
plt.xlabel("First principal component")
plt.ylabel("Second principal component")
#################
# t-SNE分析手写数据
#################
tsne = TSNE(random_state=42)
# 流式学习一般不应用在测试数据上,因此没有先fit(不需要准备,之后不会再用)再transform的过程
# 都是直接一步完成,前面的例子有用到过fit_transform,这里直接用就行.
digits_tsne = tsne.fit_transform(digits.data)
plt.figure(figsize=(10, 10))
plt.xlim(digits_tsne[:, 0].min(), digits_tsne[:, 0].max() + 1)
plt.ylim(digits_tsne[:, 1].min(), digits_tsne[:, 1].max() + 1)
for i in range(len(digits.data)):
# 将数据实际绘制成文本,而不是散点
plt.text(digits_tsne[i, 0], digits_tsne[i, 1], str(digits.target[i]),
color=colors[digits.target[i]],
fontdict={'weight': 'bold', 'size': 9})
plt.xlabel("t-SNE feature 0")
plt.xlabel("t-SNE feature 1")
plt.show()
06 聚类 k均值聚类
从名字上也能猜出来个大概,就是在分类的基础上在做归组处理.
聚类中的组成为簇(cluster).
同一cluster的数据点都非常相似,不同cluster的数据点都非常不同.
06_01 k均值聚类
怎么感觉涉及到Kxxx的都是最简单的,比如K邻近算法.
K均值聚类也是最简单最常用的算法.
# 数据聚类_K均值聚类 快速演示
# 原理:
# 1. 根据设置参数N创建N个cluster
# 2. 将各个数据点分配给最近的cluster
# 3. 计算各个cluster的平均值,并标记成cluster中心点
# 4. 迭代执行step2,3, 直到cluster的分配不再发生变化,算法结束.
# 理解:
# 算法迭代过程中,cluster的中心会发生偏移,也就会导致数据点的分配也会发生变化,
# cluster中数组一直都在变化,但是每次都会保留上一次的结果,通过数据元素匹配结束循环应当是最有效的方式.
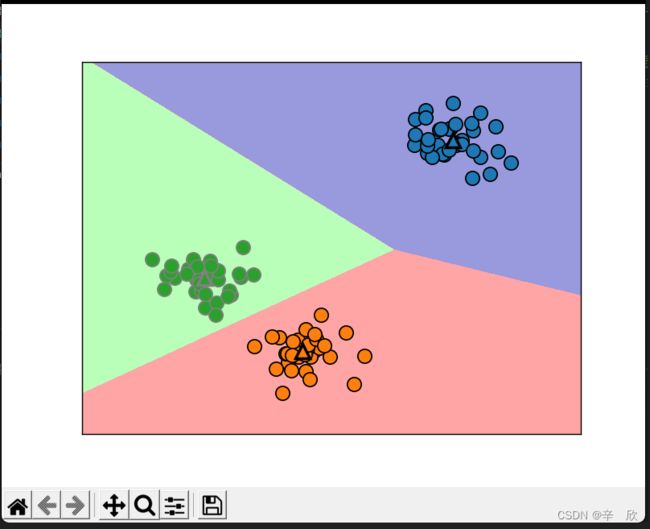
# 说明:
# 图中的三角形为对应cluster的中心
import mglearn
import matplotlib.pyplot as plt
# 算法演示
mglearn.plots.plot_kmeans_algorithm()
# 决策边界
mglearn.plots.plot_kmeans_boundaries()
plt.show()
06_02 k均值聚类简单使用
# 数据聚类_K均值聚类使用
import mglearn
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
# 生成模拟的二维数据
X, y = make_blobs(random_state=1)
# 构建聚类模型
# n_clusters 设置预先想定的簇个数
kmeans = KMeans(n_clusters=3)
kmeans.fit(X)
# labels_ 标记簇的种类, 有点像分类种的target属性,
# 不同的是labels_只负责标记簇,并不知道簇的实际种类.
# In[2]: kmeans.labels_
# Out[2]:
# array([1, 0, 0, 0, 2, 2, 2, 0, 1, 1, 0, 0, 2, 1, 2, 2, 2, 1, 0, 0, 2, 0,
# 2, 1, 0, 2, 2, 1, 1, 2, 1, 1, 2, 1, 0, 2, 0, 0, 0, 2, 2, 0, 1, 0,
# 0, 2, 1, 1, 1, 1, 0, 2, 2, 2, 1, 2, 0, 0, 1, 1, 0, 2, 2, 0, 0, 2,
# 1, 2, 1, 0, 0, 0, 2, 1, 1, 0, 2, 2, 1, 0, 1, 0, 0, 2, 1, 1, 1, 1,
# 0, 1, 2, 1, 1, 0, 0, 2, 2, 1, 2, 1])
# predict
# 可以用于测试数据上,但是测试数据会使用训练数据的簇中心,
# 也就是说新数据不会改变既有模型,而是顺应既有模型
# 如果predict使用的是训练数据,那么输出结果与labels_一致
# In [3]: kmeans.predict(X)
# Out[3]:
# array([1, 0, 0, 0, 2, 2, 2, 0, 1, 1, 0, 0, 2, 1, 2, 2, 2, 1, 0, 0, 2, 0,
# 2, 1, 0, 2, 2, 1, 1, 2, 1, 1, 2, 1, 0, 2, 0, 0, 0, 2, 2, 0, 1, 0,
# 0, 2, 1, 1, 1, 1, 0, 2, 2, 2, 1, 2, 0, 0, 1, 1, 0, 2, 2, 0, 0, 2,
# 1, 2, 1, 0, 0, 0, 2, 1, 1, 0, 2, 2, 1, 0, 1, 0, 0, 2, 1, 1, 1, 1,
# 0, 1, 2, 1, 1, 0, 0, 2, 2, 1, 2, 1])
# cluster_centers_ 存放簇中心
# In [2]:
# ...: kmeans.cluster_centers_
# Out[2]:
# array([[ -1.4710815 , 4.33721882],
# [-10.04935243, -3.85954095],
# [ -6.58196786, -8.17239339]])
########################
# 绘制散点图 簇个数 = 分类数
########################
# 使用K均值聚类算法生成的聚类绘制散点图
mglearn.discrete_scatter(X[:, 0], X[:, 1], kmeans.labels_, markers='o')
# 使用簇中心点绘制散点图
# 结合上面[cluster_centers_]的输出结果理解下面.
# [0, 1, 2] 是因为在初始化算法的时候就已经假定好了有3个簇
mglearn.discrete_scatter(
kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], [0, 1, 2],
markers='^', markeredgewidth=2)
########################
# 绘制散点图 簇个数 != 分类数
########################
fig, axes = plt.subplots(1, 2, figsize=(10, 5))
# 使用2个簇中心:
kmeans = KMeans(n_clusters=2)
kmeans.fit(X)
mglearn.discrete_scatter(X[:, 0], X[:, 1], kmeans.labels_, ax=axes[0])
# 使用5个簇中心:
kmeans = KMeans(n_clusters=5)
kmeans.fit(X)
mglearn.discrete_scatter(X[:, 0], X[:, 1], kmeans.labels_, ax=axes[1])
plt.show()
06_03 k均值聚类 失败案例
根据K均值聚类的原理,反复迭代模型会找到一个簇的中心.
试想一下如果时环形数据源的话会怎么样…其实都不用实验就能想象出来,至少簇中心可定不可能是中心
因为算法是邻近点算均值.
# 数据聚类_K均值聚类 失败案例
# 3种失败案例
import mglearn
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
##############################
# 失败案例 环形数据
##############################
# 失败内容: 无法找到环形的中心点, 而是找到相邻数据的中心点
X, y = make_moons(n_samples=200, noise=0.05, random_state=0)
# 将数据聚类成2个簇
kmeans = KMeans(n_clusters=2)
kmeans.fit(X)
# 画出簇分配和簇中心
plt.scatter(X[:, 0], X[:, 1], c=kmeans.labels_, cmap=mglearn.cm2, s=60)
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1],
marker='^', c=[mglearn.cm2(0), mglearn.cm2(1)], s=100, linewidth=2)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
##############################
# 失败案例 不同分类点距离很接近的数据
##############################
# 失败内容: 簇不准确, 会包含相邻簇中距离当前簇距离很近的点.
# cluster_std用于控制不同簇的范围
# 这里使用了 1和0.5 相对于2.5 都要远一些.
# 创建新画布
plt.figure()
X_varied, y_varied = make_blobs(n_samples=200,
cluster_std=[1.0, 2.5, 0.5],
random_state=170)
kmeans = KMeans(n_clusters=3, random_state=0)
kmeans_fit = kmeans.fit(X_varied)
y_pred = kmeans.fit_predict(X_varied)
mglearn.discrete_scatter(X_varied[:, 0], X_varied[:, 1], y_pred)
mglearn.discrete_scatter(kmeans_fit.cluster_centers_[
:, 0], kmeans_fit.cluster_centers_[:, 1], [0, 1, 2], markers='D')
plt.legend(["cluster 0", "cluster 1", "cluster 2"], loc='best')
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
##############################
# 失败案例 带有方向的数据源
##############################
# 失败原因: k均值聚类不考虑数据方向,只关心距离是否相近.
# 无法准确带有方向数据的中心点,出错原因类似环形数据
# 创建新画布
plt.figure()
# 生成一些随机分组数据 创建3分类测试数据
X, y = make_blobs(random_state=170, n_samples=600)
# In[6]: set(y)
# Out[6]: {0, 1, 2}
# 生成随机数
rng = np.random.RandomState(74)
# 简单说一下RandomState
# 生成伪随机数函数, 取值范围 0~1
# rand函数用于取随机数,无参情况下返回1个随机数,有参情况下,返回指定个数的随机数
# 由此可见RandomState内部是应当是维护一个随机数组的,保留numpy的特性
# In [22]: rng
# Out[22]: RandomState(MT19937) at 0x275C9C5C940
# In [23]: rng.rand()
# Out[23]: 0.42384573800413594
# In [24]: rng.rand(4)
# Out[24]: array([0.80487959, 0.02949612, 0.52576831, 0.78733602])
# 生成 2 * 2 结构的随机数
transformation = rng.normal(size=(2, 2))
# 变换数据使其拉长
# 结合下面的例子理解如何做到数据放大的
X = np.dot(X, transformation)
# In [26]: x
# Out[26]:
# array([[1, 2],
# [1, 2]])
# In [27]: y
# Out[27]:
# array([[0.5, 0.8],
# [0.5, 0.9]])
# In [24]: np.dot(x,y)
# Out[24]:
# array([[1.5, 2.6],
# [1.5, 2.6]])
# In [25]: np.dot(y,x)
# Out[25]:
# array([[1.3, 2.6],
# [1.4, 2.8]])
# 将数据聚类成3个簇
kmeans = KMeans(n_clusters=3)
kmeans_fit = kmeans.fit(X)
y_pred = kmeans.predict(X)
# # 画出簇分配和簇中心
plt.scatter(X[:, 0], X[:, 1], c=y_pred, cmap=mglearn.cm3)
plt.scatter(kmeans_fit.cluster_centers_[:, 0], kmeans_fit.cluster_centers_[:, 1],
marker='D', c=[0, 1, 2], s=100, linewidth=2, cmap='Dark2')
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.show()
06_04 PCA NMF K均值聚类 处理人脸图像的对比
关于数据的重建不同的算法有自己的重建方式:
- PCA 主成分分析
最好理解反向transform就可以
通过 pca.inverse_transform(pca.transform(X_test)) 来实现重建 - NMF 非负矩阵分析
通过扩张放大的思路实现重建
具体为:np.dot(nmf.transform(X_test), nmf.components_) - K均值聚类
这个更简单,找到簇的中心点就行
具体为: kmeans.cluster_centers_[kmeans.predict(X_test)]
# 数据聚类_PCA NMF K均值聚类 对比
# 处理概要:
# 1. 准备数据
# 2. 分别使用3种算法计算人脸数据
# 3. 使用step2的数据直接绘图
# 4. 将step2的数据根据各个算法进行重建
# 5. 将step4种重建好的数据进行绘图
# 6. 观察各个算法直接出图与重建后的图,以及原始图之间的关系
# 观察结论:
# 1. NMF 与算法介绍的一样,它的初衷是保留数据方向并提取主成分
# 直接出图:
# 从图中可以看出,NMF的直接计算结果 大概描述出了数据轮廓,因此能判定数据方向
# 重建出图:
# 轮廓更多了一些,对于计算机而言,细节更多了些,但对于人眼观察缺失细节
# 2. PCA 算法目的是不考虑方向只关心主成分
# 直接出图:
# 对于人来说也就是有个人影, 对于计算机来说可以使用大概的轮廓进行模糊匹配
# 重建出图:
# 人脸大部分可以识别出来,但是受限与算法,更NMF一样缺失了不少细节.
# 就有点像素描,虽然细节少但可以很直观确认出是谁.
# 3. K均值聚类
# 直接出图:
# 没想到可以识别出人脸的大部分数据,从底色来看,基本上都识别出来了.
# 想想也是,毕竟它没删数据,只是聚隆数据,并没有删细节
# 重建出图:
# 人脸细节保留了很多,但是图片多多少少出现了些重影,原因可能是聚拢算法是数据产生了位移.
# 每个算法都针对特有的需求,没有通用算法,使用时需要留意.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.cluster import KMeans
from sklearn.decomposition import PCA
from sklearn.decomposition import NMF
from sklearn.datasets import fetch_lfw_people
###################
# 准备人脸数据
###################
# min_faces_per_person=20 每人最少20张人脸图片
people = fetch_lfw_people(min_faces_per_person=20, resize=0.7)
image_shape = people.images[0].shape
# 每人人脸图像采样最多50个
mask = np.zeros(people.target.shape, dtype=np.bool)
# 标记可以取得的人脸数据位置为true
for target in np.unique(people.target):
mask[np.where(people.target == target)[0][:50]] = 1
# 通过标记取得可用数据
X_people = people.data[mask]
y_people = people.target[mask]
# 数据拆分
X_train, X_test, y_train, y_test = train_test_split(
X_people, y_people, stratify=y_people, random_state=0)
###################
# NMF, PCA, KMEANS算法
###################
# 非负矩阵拆分 NMF
nmf = NMF(n_components=100, random_state=0)
nmf.fit(X_train)
# 主成分提取 PCA
pca = PCA(n_components=100, random_state=0)
pca.fit(X_train)
# K均值聚类 KMEANS
kmeans = KMeans(n_clusters=100, random_state=0)
kmeans.fit(X_train)
###################
# 通过各模型的计算结果重建数据
###################
# 主成分提取 PCA
# 重建原理: 先筛选出主要成分,然后通过主要成分反向补全人脸数据
X_reconstructed_pca = pca.inverse_transform(pca.transform(X_test))
# K均值聚类
# 重建原理: 为了重建,需要找到每个类别的簇中心点
# 提示:
# 对于训练数据 labels_ 与 predict 的结果一致
# 对于测试数据只能使用 predictzhua
X_reconstructed_kmeans = kmeans.cluster_centers_[kmeans.predict(X_test)]
# 非负矩阵拆分 NMF
# 重建原理: 找出带有方向部分的主成分,然后根据成分个数拉伸放大
X_reconstructed_nmf = np.dot(nmf.transform(X_test), nmf.components_)
###################
# 画图 各算法直接计算结果出图
###################
fig, axes = plt.subplots(3, 5, figsize=(8, 8),
subplot_kw={'xticks': (), 'yticks': ()})
fig.suptitle("Extracted Components")
# In [9]: lable1
# Out[9]:
# array([[1, 2],
# [3, 4]])
# In [10]: values
# Out[10]:
# array([[ 7963.92759169, -2931.3518914 , 3360.79428745],
# [ 7964.28495515, -2930.99452794, 3361.15165092],
# [ 7965.60367246, -2929.67581063, 3362.47036823]])
# In [8]: for label, score in zip(lable1,values):
# ...: print("{}:{}".format(label,score))
# ...:
# [1 2]:[ 7963.92759169 -2931.3518914 3360.79428745]
# [3 4]:[ 7964.28495515 -2930.99452794 3361.15165092]
# 思路: 一次设置一列, 1列包含3个算法
for ax, comp_kmeans, comp_pca, comp_nmf in zip(
axes.T, kmeans.cluster_centers_, pca.components_, nmf.components_):
ax[0].imshow(comp_kmeans.reshape(image_shape), cmap='PRGn_r')
ax[1].imshow(comp_pca.reshape(image_shape), cmap='viridis')
ax[2].imshow(comp_nmf.reshape(image_shape), cmap='Dark2')
axes[0, 0].set_ylabel("kmeans")
axes[1, 0].set_ylabel("pca")
axes[2, 0].set_ylabel("nmf")
###################
# 画图 将各算法计算结果反向重建后出图
###################
fig, axes = plt.subplots(4, 5, subplot_kw={'xticks': (), 'yticks': ()},
figsize=(8, 8))
fig.suptitle("Reconstructions")
for ax, orig, rec_kmeans, rec_pca, rec_nmf in zip(
axes.T, X_test, X_reconstructed_kmeans, X_reconstructed_pca,
X_reconstructed_nmf):
ax[0].imshow(orig.reshape(image_shape))
ax[1].imshow(rec_kmeans.reshape(image_shape), cmap='PRGn_r')
ax[2].imshow(rec_pca.reshape(image_shape), cmap='viridis')
ax[3].imshow(rec_nmf.reshape(image_shape), cmap='Dark2')
axes[0, 0].set_ylabel("original")
axes[1, 0].set_ylabel("kmeans")
axes[2, 0].set_ylabel("pca")
axes[3, 0].set_ylabel("nmf")
plt.show()
06_05 K均值聚类的优缺点
- 优点:
- 相对容易理解和实现,运行速度也较快,因为它就找用不到拆分再计算
- 可以增加数据元的特征,之前我们有过一个例子,使用3分类的数据源是可以用5个簇来表示的,
对于拆分提取主成分的NMF和PCA算法而言这是不可能办到的。对于人脸数据而言簇越多,还原越细节化。
- 缺点:
- 对簇的形状要求太严格。像分类数据间距较近,带有方向数据比如环形数据,都不太适合使用这种算法
- K均值聚类的算法是嵌套找出簇中心,总要从某个点开始, 开始的位置很影响结果,算法会默认先算10次位置
然后取最佳结果,但是即便是最佳结果也可能与真实结果有偏差。 - 虽然可以增加簇个数来达到认为增加数据特征的目的,但是很多情况下并不知道拿到手数据的簇实际个数,
很可能设定的值比元数据簇数还少。
07 聚类 凝聚聚类
凝聚聚类相对与K均值聚类解决了:
- 随机起点问题
- 无法确定元数据的簇个数
# 数据聚类_凝聚聚类 快速演示
# 凝聚聚类原理:
# 1. 将每个数据点都看成簇
# 2. 递归合并两个相似的簇,知道簇的个数缩减到指定的个数为止
# 判断相似簇的参数有:
# ward:
# ward 挑选两个簇来合并,使得所有簇中的方差增加最小。这通常会得到大小差不多相等的簇
# average:
# average 链接将簇中所有点之间平均距离最小的两个簇合并。
# complete:
# complete 链接(也称为最大链接)将簇中点之间最大距离最小的两个簇合并。
# 其中 ward 适合分类数据中各类个数差别不大的数据源.
import mglearn
import matplotlib.pylab as plt
######################
# 凝聚聚类分层过程
######################
mglearn.plots.plot_agglomerative_algorithm()
plt.figure()
######################
# 表示每次迭代产生的层
######################
# 只看每层的合并点是否对就行, 上面的编号是算法分析的过程不用关心
# 这个图看起来有点像地图的海拔图
mglearn.plots.plot_agglomerative()
plt.show()
07_01 凝聚聚类如何使用
# 数据聚类_凝聚聚类 使用方法
# 概要:
# 1. 使用同样的数据源(参照前面的例子,使用的是K均值聚类无法完全区分的数据源)
# 2. 先画出凝聚聚类
# 3. 再画出K均值聚类
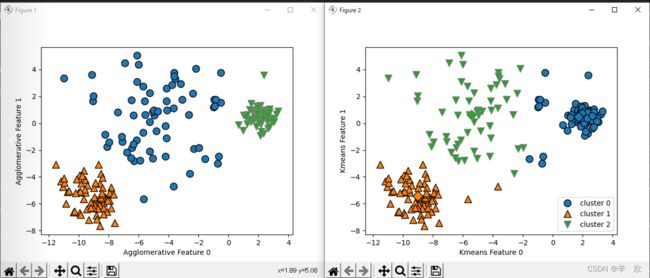
# 比较结果:
# 凝聚聚类的算法好像能比较好的区分数据, 各个类别划分的很清晰,没有噪点.
import mglearn
import matplotlib.pyplot as plt
from sklearn.cluster import AgglomerativeClustering
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
#######################
# 凝聚聚类
#######################
X, y = make_blobs(n_samples=200,
cluster_std=[1.0, 2.5, 0.5],
random_state=170)
agg = AgglomerativeClustering(n_clusters=3)
# 凝聚聚类由于算法限制,只能用于训练数据,因此没有predict方法, 但可以使用fit_predict
assignment = agg.fit_predict(X)
mglearn.discrete_scatter(X[:, 0], X[:, 1], assignment)
# 凝聚聚类形成的簇好像没有簇的中心点坐标Agglomerative,属性里没查到.
plt.xlabel(" Feature 0")
plt.ylabel("Agglomerative Feature 1")
#######################
# k均值聚类 之前的例子,方便对比
#######################
plt.figure()
X_varied, y_varied = make_blobs(n_samples=200,
cluster_std=[1.0, 2.5, 0.5],
random_state=170)
kmeans = KMeans(n_clusters=3, random_state=0)
kmeans_fit = kmeans.fit(X_varied)
y_pred = kmeans.fit_predict(X_varied)
mglearn.discrete_scatter(X_varied[:, 0], X_varied[:, 1], y_pred)
mglearn.discrete_scatter(kmeans_fit.cluster_centers_[
:, 0], kmeans_fit.cluster_centers_[:, 1], [0, 1, 2], markers='D')
plt.legend(["cluster 0", "cluster 1", "cluster 2"], loc='best')
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.show()
07_02 凝聚聚类优缺点
- 优点:
- 能很好的区分相近点的类别
- 不用关心原始数据的簇个数
- 缺点:
- 对于带有方向的复杂图形(比如环形数据)还是不能正确区分.
08 聚类 DBSCAN 带有噪点的空间凝聚
DBSCAN(density-based spatial clustering of applications with noise)
具有噪声的基于密度的空间聚类应用
08_01 DBSCAN原理
# 数据聚类_DBSCAN 快速演示
# DBSCAN 本质上也是凝聚, 只是相对于凝聚聚类它的方法稍显不同,它是通过拥挤程度来区分簇的.
# 影响DBSCAN判断拥挤程度的两个重要参数:
# 1. min_samples 用于描述数据点个数
# 2. eps 用于描述距离
# 原理大概:
# 1.确定一个簇标记 (eps范围内的数据点个数大于等于min_samples)
# 2.用标记好的簇去影响eps范文内还未标记的点,
# 3.搜寻这个簇,标记这个簇能影响到的所有点,直到找不出为止
# 4. 重复1~3步骤,直到所有点都被标记完为止.
# 详细步骤:
# 1. 首先选取数据中的一个随机点
# 2. 找出在eps范围内的所有数据点
# 3. 如果找出的数据点个数小于min_samples那么(1)中的点就被标记成噪声,说明该点不属于任何簇
# 4. 反之,(1)中的点就会被标记成核心样本,并会分配给一个新的簇标检
# 5. 重新看一下(2)中的数据点, 对还没有分配簇标签的数据点,统一分配成(1)的簇标签
# 6. 依次访问(2)中被标记的数据点,然后再以eps为范围搜寻邻近点,再标记
# 7. 重复执行1~6的步骤,知道无法再找到新的核心样本为止
# 8. 再随机抽取一个数据点(既不是噪声,也没标记簇) 重复1~7的动作 直到标记完所有的点为止.
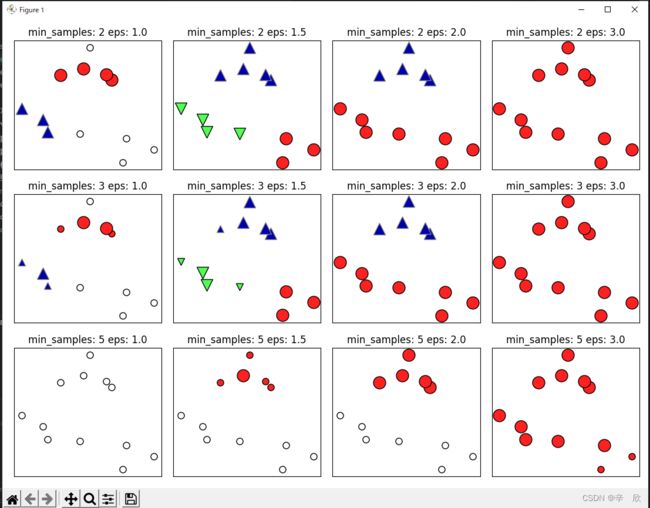
# 图怎么看:
# 1. 实心大图标为 "核心数据"
# 2. 实心小图标为 "边界点" (卡着eps距离的点)
# 3. 空心图标为 "噪声"
# 4. 图中距离说明了, min_sample和eps是如何影响模型判断的
# 参数影响:
# 1. eps设置的太小,那么每个数据点将变成噪点,反之所有的数据点都可能会变成一个簇
# 2. min_samples设置的越大,核心点越少,噪点越多.
import mglearn
import matplotlib.pylab as plt
mglearn.plots.plot_dbscan()
plt.show()
08_02 DBSCAN使用
DBSCAN依旧只能用于训练数据.
# 数据聚类_DBSCAN 使用方法
# 概要:
# 1. 创建数据源
# 2. 使用之前学过的方法,先对数据进行预处理(缩放)
# 3. 将缩放后的数据使用DBSCAN进行处理
# 4. 绘制散点图, 数据源使用(2), 类别目标使用(3)
# 注意:
# 书中原话:
# 在使用DBSCAN 时,你需要谨慎处理返回的簇分配。如果使用簇标签对另一个数据进行
# 索引,那么使用-1 表示噪声可能会产生意料之外的结果。
# 我理解: 一般使用方法为,谁判别的类别,数据源也已应当用谁的,这样是最准确的,
# 但这个例子中,源和目标分别使用了两个算法计算结果,可能就是为了演示说明用,
# 如果DBSCAN计算结果中有-1产生的话,需要谨慎使用结果.
import mglearn
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from sklearn.preprocessing import StandardScaler
from sklearn.cluster import DBSCAN
#################
# 数据源
#################
X, y = make_moons(n_samples=200, noise=0.05, random_state=0)
#################
# 缩放数据
#################
# 将数据缩放成平均值为0、方差为1
scaler = StandardScaler()
scaler.fit(X)
X_scaled = scaler.transform(X)
#################
# 使用DBSCAN算法来判别类别
#################
# 注意: DBSCAN算法只能用在训练数据上,因此没有predict方法
# 默认情况下:
# eps=0.5
# min_samples=5
dbscan = DBSCAN()
clusters = dbscan.fit_predict(X_scaled)
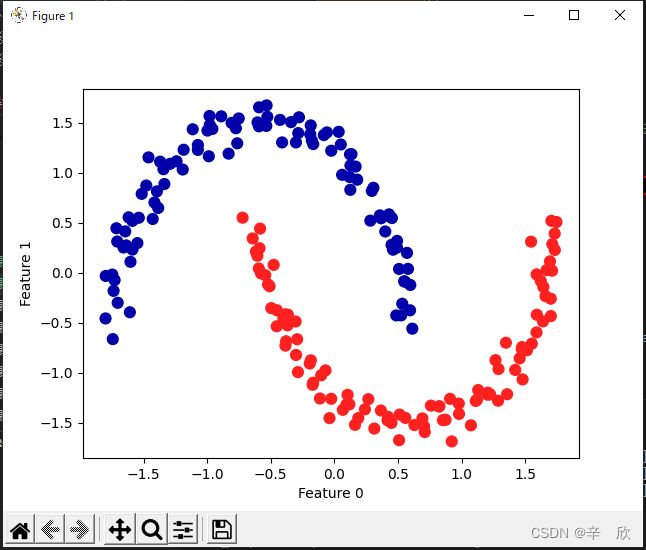
# 这个例子中好像都判别正确了
# In [2]: clusters
# Out[2]:
# array([0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1,
# 0, 1, 0, 1, 1, 1, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1,
# 1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0,
# 0, 1, 0, 0, 1, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 1, 1, 0, 0, 0,
# 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 0,
# 0, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1, 1, 0, 0,
# 0, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 1, 1, 1, 0, 0,
# 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 1, 1,
# 1, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1,
# 0, 1], dtype=int64)
# 如果这么设置的话,就会产生-1,也就是结果不正确 最终显示的图片来看,确识也不对.
# In [3]: dbscan = DBSCAN(eps=0.2)
# In [4]: clusters = dbscan.fit_predict(X_scaled)
# In [5]: clusters
# Out[5]:
# array([ 0, 1, 2, -1, 3, 3, 0, 1, 0, 1, 6, 4, 3, 1, 5, 0, 6,
# 4, 6, 6, 3, 1, 6, 1, 6, 4, 3, 3, 4, 6, 0, -1, 1, 2,
# 6, 3, 4, 0, 5, 2, 1, 6, 6, 4, 1, 6, 0, 5, 4, 1, 6,
# 4, 3, -1, 1, 6, 6, 1, 6, 6, 4, 5, 3, 0, 1, 5, 6, 1,
# 6, 5, 1, 5, 1, -1, 1, 5, 2, 0, 6, 1, 3, 6, 1, 3, 2,
# 6, 0, 6, 1, 3, 6, 0, 3, 6, 3, 3, 3, 4, 5, 4, -1, 3,
# 6, 0, 5, 2, 5, 6, 1, 6, 6, 6, 6, 5, 0, 1, 6, 3, 1,
# 0, 0, 5, 2, 6, 2, 5, 0, 4, 1, 3, 0, 6, 5, 4, 1, 3,
# 1, 5, 3, 0, 4, 2, 6, 6, 6, 0, 4, 1, 6, 2, 1, 1, 0,
# 6, 1, 6, 1, 4, 6, 6, 4, 1, 6, 1, 1, 3, 6, 1, 1, 1,
# 6, -1, 5, 5, 4, 1, 3, 5, 5, 6, 1, 5, 3, 1, 3, 6, 6,
# 1, 5, 6, 5, 6, 0, 0, 2, 6, 3, 4, 6, 3], dtype=int64)
#################
# 绘制散点图
#################
# 绘制簇分配
plt.scatter(X_scaled[:, 0], X_scaled[:, 1], c=clusters, cmap=mglearn.cm2, s=60)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.show()
09 聚类_聚类算法的对比与评估
目前为止对于聚类算法已经学过3个了,再评估之前先回顾下算法的处理概要
- K均值聚类(核心: 再计算中心点):
- 根据参数随机创建N个cluster, 然后根据参数(基于方差,基于平局值,基于中心点距离)
将附近的点吸纳为自己簇的成员,然后重新计算簇的中心点,直到中心点为止固定为止.
- 根据参数随机创建N个cluster, 然后根据参数(基于方差,基于平局值,基于中心点距离)
- 凝聚聚类(核心: 引力最大的两点互项吸引):
- 将每个点先都看成簇,然后找关系(基于最短簇平局距离最短,基于最短距离)组队,
直到所有的数据点都合并成簇,且簇的个数与参数一致位置数.
- 将每个点先都看成簇,然后找关系(基于最短簇平局距离最短,基于最短距离)组队,
- DBSCAN 带有噪点的空间凝聚(核心: 范围影响)
- 随机找一点作为起始点,根据参数(范围,成员个数)来尝试标记这个点为簇,
标记成功后,就开始影响范围内的其它数据点,然后开始组队,组队成功后的成员享有优先组队权,
继续向下发展成员,直到无下线为止.使用同样方法再去开一个新簇,循环套路,直到所有点都标记过为止.
- 随机找一点作为起始点,根据参数(范围,成员个数)来尝试标记这个点为簇,
接下会用两种方法来评估上面的3种聚类算法.
09_01 用真实值评估聚类
此类评估是基于已经有数据的真实目标值,然后用这些值与算法的计算结果进行比对,然后对记过进行评估
有两种方法可以评估聚类算法的准确性:
- ARI (adjusted rand index): 调整rand 指数
- 位置: from sklearn.metrics.cluster import adjusted_rand_score
- NMI (normalized mutual information): 归一化互信息
- 位置: from sklearn.metrics.cluster import normalized_mutual_info_score
这两个在使用上都差不多,只是包的位置和方法名不一样.
下面例子中使用ARI来举例说明:
# 数据聚类_真实值评估
# 概要:
# 1. 创建数据
# 2. 绘制4副图
# 2.1 利用随机数打乱原有结果的绘图
# 2.2 K均值聚类计算结果的绘图
# 2.3 凝聚聚类计算结果的绘图
# 2.4 带有噪点的空间凝聚计算结果的绘图
# 3. 使用聚类评估函数将结果与真实值之间进行比对
# 结论: 对于ARI来说 取值是0~1 越趋近于1 模型越完美.
import mglearn
import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics.cluster import adjusted_rand_score
# from sklearn.metrics.cluster import normalized_mutual_info_score
from sklearn.cluster import KMeans
from sklearn.cluster import DBSCAN
from sklearn.cluster import AgglomerativeClustering
from sklearn.datasets import make_moons
from sklearn.preprocessing import StandardScaler
###############
# 创建数据
###############
X, y = make_moons(n_samples=200, noise=0.05, random_state=0)
###############
# 缩放数据
###############
# 将数据缩放成平均值为0、方差为1
scaler = StandardScaler()
scaler.fit(X)
X_scaled = scaler.transform(X)
###############
# 创建4个绘图
###############
fig, axes = plt.subplots(1, 4, figsize=(15, 3),
subplot_kw={'xticks': (), 'yticks': ()})
# 列出要使用的算法
algorithms = [KMeans(n_clusters=2), AgglomerativeClustering(n_clusters=2),
DBSCAN()]
###############
# 第一个图就是加入随机数,尽量让结果与实际不符来验证adjusted_rand_score
###############
# 创建一个随机的簇分配,作为参考
random_state = np.random.RandomState(seed=0)
random_clusters = random_state.randint(low=0, high=2, size=len(X))
# In [2]: random_clusters
# Out[2]:
# array([0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1,
# 1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 1, 0, 1,
# 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 0, 1, 0,
# 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1,
# 1, 0, 1, 1, 0, 0, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0,
# 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1,
# 1, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0, 0, 0, 1,
# 0, 1, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0,
# 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1,
# 0, 0])
# 绘制随机分配
axes[0].scatter(X_scaled[:, 0], X_scaled[:, 1], c=random_clusters,
cmap=mglearn.cm3, s=60)
axes[0].set_title("Random assignment - ARI: {:.2f}".format(
adjusted_rand_score(y, random_clusters)))
###############
# 将其它3中算法的结果值与真实值进行比较
###############
for ax, algorithm in zip(axes[1:], algorithms):
# 绘制簇分配和簇中心
clusters = algorithm.fit_predict(X_scaled)
ax.scatter(X_scaled[:, 0], X_scaled[:, 1], c=clusters,
cmap=mglearn.cm3, s=60)
ax.set_title("{} - ARI: {:.2f}".format(algorithm.__class__.__name__,
adjusted_rand_score(y, clusters)))
plt.show()
09_02 在没有真实值的情况下评估聚类
聚类的算法中有很多只能应用在训练数据上,既然已经知道结果有何必再费心思去算一遍,
况且真实世界中有结果的数据集很少,所以就必须有一个标准来评估算法的结果.
而之前提到过的ARI和NMI的使用价值是去评估已有或新算法的准确率.
用于评估无真实值的算法模型有:
- 轮廓系数 (silhouette coeffcient)
轮廓系数用于描述簇的紧致度,越越大越好, 1为最大值. 轮廓系数对于复杂形状的数据表现并不太好.
轮廓系数评估得分:
# 数据聚类_无真实值评估_轮廓系数
# 概要:
# 1. 创建数据
# 2. 绘制4副图
# 2.1 利用随机数打乱原有结果的绘图
# 2.2 K均值聚类计算结果的绘图
# 2.3 凝聚聚类计算结果的绘图
# 2.4 带有噪点的空间凝聚计算结果的绘图
# 3. 使用轮廓系数将结果与真实值之间进行比对
# 结论: 轮廓系数反映的是数据点的凝聚力,评估值并不能很好的反应模型真实水平
# 从得分中可以看出,DBSCAN的得分竟然比K均值聚类还低
import mglearn
import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics.cluster import silhouette_score
from sklearn.datasets import make_moons
from sklearn.cluster import KMeans
from sklearn.cluster import AgglomerativeClustering
from sklearn.cluster import DBSCAN
from sklearn.preprocessing import StandardScaler
# 创建数据集
X, y = make_moons(n_samples=200, noise=0.05, random_state=0)
# 将数据缩放成平均值为0、方差为1
scaler = StandardScaler()
scaler.fit(X)
X_scaled = scaler.transform(X)
# 准备绘图模板
fig, axes = plt.subplots(1, 4, figsize=(15, 3),
subplot_kw={'xticks': (), 'yticks': ()})
# 用随机数打乱结果,作为第一张图
# 创建一个随机的簇分配,作为参考
random_state = np.random.RandomState(seed=0)
random_clusters = random_state.randint(low=0, high=2, size=len(X))
# 绘制随机分配
axes[0].scatter(X_scaled[:, 0], X_scaled[:, 1], c=random_clusters,
cmap=mglearn.cm3, s=60)
axes[0].set_title("Random assignment: {:.2f}".format(
silhouette_score(X_scaled, random_clusters)))
# 绘制另外三个模型的计算结果
algorithms = [KMeans(n_clusters=2), AgglomerativeClustering(n_clusters=2),
DBSCAN()]
for ax, algorithm in zip(axes[1:], algorithms):
clusters = algorithm.fit_predict(X_scaled)
# 绘制簇分配和簇中心
ax.scatter(X_scaled[:, 0], X_scaled[:, 1], c=clusters, cmap=mglearn.cm3,
s=60)
# 看看各个模型的轮廓评估得分
ax.set_title("{} : {:.2f}".format(algorithm.__class__.__name__,
silhouette_score(X_scaled, clusters)))
plt.show()

轮廓系数失败的原因:
其实所有模型都有这方面的问题,模型归根结底都是分析数据.
计算机容易判断的数据:
比如 色温,色调,光线控制,数据轮廓,GPS信息等等通过算法可以剥离的这部分数据都是可以很轻松通过优化算法进行判断的.
比较难判断的数据:
比如人脸是男性还是女性, 简单通过胡子,发量判断的话想想就知道肯定不行
比如在人形图片中找到同款衣服的照片.
这些数据即便是能完美找出指定类型,算法也不见得能适用其它情况.
尝试调整DBSCAN参数并查看算法结果:
10 聚类算法在人脸数据上的表现
变换分解法的核心思想是: 尽可能的将数据简单化,尽可能的抽出主要特征.
聚类算法的核心思想是: 尽量保留数据特征,尽可能的将相近点集中.
基于聚类算法的思想,书中细分出了3中更细致的算法:
- K均值聚类
- 聚类特点:
- 算法需指定最终簇个数(簇个数可任意设定), 簇中心为这个簇的平均值.
- 无法控制噪声.
- 簇中成员分布均匀
- 聚类特点:
- 凝聚聚类
- 聚类特点:
- 算法需指定最终簇个数(簇个数可任意设定).
- 需指定寻找相近值得规则.
- 无法控制噪声
- 簇中成员分布均匀
- 聚类特点:
- 带有噪点的空间聚类
- 聚类特点:
- 无需指定簇个数,
- 可以控制噪声,
- 无法聚集大簇
- 簇的分布可能不太均匀
- 聚类特点:
我理解的聚类算法:(找西瓜仔):
- 训练数据中,每个数据的计算结果都是西瓜中的一个仔.
- 聚类算法就是找同一类西瓜仔的过程,
- K均值聚类:
- 把西瓜仔全拿出来,用预先准备好的称(个数同参数一致)这些西瓜仔,反复试,直到这几个称的重量一致为止
- 凝聚聚类:
- 根据深度,广度等标准切西瓜,切好了把每块的仔分别集中起来,放入各个碗中.
- 带有噪点的凝聚聚类:
- 用装有蓝色的针管将颜色注入西瓜中的任意仔上,等蓝色不再扩散
- 蓝色部分只有一个仔的蓝色这块直接扔掉.
- 有多个仔的,再用针管去标记这些仔,直到蓝色部分没有新仔出现为止,将蓝色部分切下来放入碗中
- 重复上面步骤,每次换一个颜色的染料,将不同颜色的西瓜放入不同的碗中 即可.
- K均值聚类:
接下来将分别使用上面所介绍的3种聚类算法来计算人脸数据.
10_01 DBSCAN计算人脸数据
DBSCAN(带有噪点的空间凝聚)
# 数据聚类_使用DBSCAN计算人脸数据
# - 带有噪点的空间聚类
# - 聚类特点:
# - 无需指定簇个数,
# - 可以控制噪声,
# - 无法聚集大簇
# - 簇的分布可能不太均匀
# 概要:
# 1. 使用人脸数据,并控制每人最多只能有50张图
# 2. 使用PCA提取人脸识别的主要成分
# 3. 查看DBSCAN在PCA过滤后数据上的表现
# 4. 学会如何调整DBSCAN的最适参数
# 5. 使用最佳参数应用DBSCAN,将聚合后的簇的人脸图片打印出来
# 观察结果:
# 预想结果: 通过最佳参数的DBSCAN计算的簇中的图片应当尽量接近
# 实际结果: 有的簇会出现完全不同的人脸图片
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.datasets import fetch_lfw_people
from sklearn.cluster import DBSCAN
##########################
# 人脸数据
##########################
people = fetch_lfw_people(min_faces_per_person=20, resize=0.7)
image_shape = people.images[0].shape
# 每人人脸图像采样最多50个
mask = np.zeros(people.target.shape, dtype=np.bool)
for target in np.unique(people.target):
mask[np.where(people.target == target)[0][:50]] = 1
X_people = people.data[mask]
y_people = people.target[mask]
##########################
# 人脸数据
##########################
# 这里用PCA预处理一下数据,因为pca不用考虑方向,对人脸数据识别较准确
# 而且适用的变换法可以缩减需要判断的数据源能效提升运行效率
pca = PCA(n_components=100, whiten=True, random_state=0)
pca.fit_transform(X_people)
X_pca = pca.transform(X_people)
##########################
# 使用带噪点的聚类算法看看主成分数据效果
##########################
# 应用默认参数的DBSCAN
dbscan = DBSCAN()
labels = dbscan.fit_predict(X_pca)
print("Unique labels: {}".format(np.unique(labels)))
# 很遗憾, DBSCAN把所有的主成分都算成噪点了. (-1 表示噪点)
# In [2]: print("Unique labels: {}".format(np.unique(labels)))
# Unique labels: [-1]
# 回想一下DBSCAN算法的重要参数, min_samples 和 eps. 即数据点数和范围
# 默认情况下之找出一类,说明参数还需要调整. 因为PCA本身没有问题.
##########################
# 如何找到DBSCAN的最佳参数设置
##########################
# 这里就是举例说明, 不要纠结为什么用1,3,5,,,这个列表,
# 在实际使用中,步长可能会拆的更细
for eps in [1, 3, 5, 7, 9, 11, 13]:
print("\neps={}".format(eps))
dbscan = DBSCAN(eps=eps, min_samples=3)
labels = dbscan.fit_predict(X_pca)
print("Clusters present: {}".format(np.unique(labels)))
print("Cluster sizes: {}".format(np.bincount(labels + 1)))
# 输出结果:
# 在我们已经大体掌训练数据分类个数的基础上,分析算法结果可以得出
# 1. 计算结果簇的个数越接近训练数据的分类数,模型越完美
# 2. 每个簇的成员个数最多不能超过50(训练数据人脸个数限定出现50个)
# 3. 计算结果表现上来看,DBSCAN的eps参数并不是越大越好
# 目前来看eps=7时, 分类个数较其它情况要细一些,但仍然与真实结果相差不小.
# 例子中假定了min_sample=3, 实际上,我们也可以用嵌套循环的方法使用不同取值来反复验证
# min_sample和eps的计算结果,然后通过簇个数和核心数来与真实数据比较以确定最佳参数.
# 如果我们手里拿到的训练数据,没有目标值的时候,可以将簇种类较多和簇成员较均匀的簇的图片打出来验证算法.
# eps=1
# Clusters present: [-1]
# Cluster sizes: [1272]
# eps=3
# Clusters present: [-1]
# Cluster sizes: [1272]
# eps=5
# Clusters present: [-1]
# Cluster sizes: [1272]
# eps=7
# Clusters present: [-1 0 1 2 3 4 5 6 7]
# Cluster sizes: [1229 3 20 5 3 3 3 3 3]
# eps=9
# Clusters present: [-1 0 1 2]
# Cluster sizes: [807 458 4 3]
# eps=11
# Clusters present: [-1 0]
# Cluster sizes: [283 989]
# eps=13
# Clusters present: [-1 0]
# Cluster sizes: [ 91 1181]
##########################
# 使用较精准的参数来设置DBSCAN,看看找出的图片
##########################
# 我们假设通过上面的方法已经找出了min_samples = 3, eps = 7
dbscan = DBSCAN(min_samples=3, eps=7)
labels = dbscan.fit_predict(X_pca)
# In[20]: labels.shape
# Out[20]: (1272,)
# 这里的循环排除了DBSCAN认为是噪点的图片
# -1 为噪点
for cluster in range(max(labels) + 1):
# 跟控制人脸出现次数时使用的方法一致
# 先设定一个值,然后将数组中与这个值相同的位置标记成true,其它的标记成false
# 然后用标记好的坐标去筛选数组.
mask = labels == cluster
# 由于mask里存的是位置的True和False. True为1 False为0
# sum计算的是本次循环满足cluster值的簇个数总数
n_images = np.sum(mask)
fig, axes = plt.subplots(1, n_images, figsize=(n_images * 1.5, 4),
subplot_kw={'xticks': (), 'yticks': ()})
for image, label, ax in zip(X_people[mask], y_people[mask], axes):
# ax.imshow(image.reshape(image_shape), vmin=0, vmax=1)
ax.imshow(image.reshape(image_shape))
ax.set_title(people.target_names[label].split()[-1])
plt.show()
因为这个例子出的图很多,我们就抽取典型的来看:
受限于算法,簇中人物并不能保证都是同一人.即使是使用了较准的参数也是如此
10_02 K均值聚类计算人脸数据
# 数据聚类_使用K均值聚类计算人脸数据
# - K均值聚类
# - 聚类特点:
# - 算法需指定最终簇个数(簇个数可任意设定), 簇中心为这个簇的平均值.
# - 无法控制噪声.
# - 簇中成员分布均匀
# 概要:
# 1. 使用人脸数据,并控制每人最多只能有50张图
# 2. 使用PCA提取人脸识别的主要成分
# 3. 查看KMeans在PCA过滤后数据上的表现
# 观察结果:
# 因为KMeans算法是计算簇的平均值,因此,簇中心点重建后的图片更趋近于大众脸
# 也就是簇中成员图片的平局表现.
# KMeans算法的起始点是随机的,因此结果会与我的有不一致的地方
# 同样也应为平局值得特性,结果并不太让人满意.例子中使用了10个簇来调用kmeans,
# 当然个数可以随意指定,这点在之前的例子中已经验证过了,簇得个数指定越多,说明细节关注就越多,
# 理论上是可以但是太多得细节反而观察起来麻烦.
# 比如: 设置100个簇, Kmeans也成功合成了100个簇, 现在需要找到头向上,手捂住嘴,人物是xxx的图片,
# 那么就需要先逐一排查100个簇,先找到哪组簇是符合上面规则的,才能做下一步.这一步只能人工完成,
# 因为Kmenas算法在合成簇的参数里,并没有能设置其它参数的机会,只能单纯的合成簇,至于合成的簇是什么
# Kmeans并不知道是什么,也不知道怎么用,也是比较符合无人监督算法地.
import mglearn
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.datasets import fetch_lfw_people
from sklearn.cluster import KMeans
##########################
# 人脸数据
##########################
people = fetch_lfw_people(min_faces_per_person=20, resize=0.7)
image_shape = people.images[0].shape
# print(image_shape)
# 每人人脸图像采样最多50个
mask = np.zeros(people.target.shape, dtype=np.bool)
for target in np.unique(people.target):
mask[np.where(people.target == target)[0][:50]] = 1
X_people = people.data[mask]
y_people = people.target[mask]
##########################
# 人脸数据
##########################
# 这里用PCA预处理一下数据,因为pca不用考虑方向,对人脸数据识别较准确
# 而且适用的变换法可以缩减需要判断的数据源能效提升运行效率
pca = PCA(n_components=100, whiten=True, random_state=0)
pca.fit_transform(X_people)
X_pca = pca.transform(X_people)
km = KMeans(n_clusters=10, random_state=0)
labels_km = km.fit_predict(X_pca)
print("Cluster sizes k-means: {}".format(np.bincount(labels_km)))
# 单从簇成员来看,成员分布情况较DBSCAN要好一些
# 但是个数上大多超过了50, 说明准确性还是差了一些
# In [2]: print("Cluster sizes k-means: {}".format(np.bincount(labels_km)))
# Cluster sizes k-means: [ 95 358 122 121 10 73 93 87 190 123]
##########################
# 重建簇中图片并显示
##########################
# 注意: 是重建,不是直接显示,因此需要使用inverse_transform来补充被PCA算法删减的数据
# vmin, vmax 参数不知到怎么回事,设置上图片就打印不出来.
fig, axes = plt.subplots(2, 5, subplot_kw={'xticks': (), 'yticks': ()},
figsize=(12, 4))
for center, ax in zip(km.cluster_centers_, axes.ravel()):
ax.imshow(pca.inverse_transform(center).reshape(image_shape),
vmin=0, vmax=1)
##########################
# 重建簇中图片并显示
##########################
# plot_kmeans_faces 没有函数帮助, 接口大概都能看懂.
# 算法内步骤:
# 1. 使用PCA结果重建图像 放在第一列位置
# 2. 用KMeans结果中的簇的前5个数据和后5个数据重建图像,放到2~11列位置
# 3. 画3个框 框起来 1
mglearn.plots.plot_kmeans_faces(km, pca, X_pca, X_people,
y_people, people.target_names)
plt.show()
这个例子的图没法展示,因为参数[vmin=0, vmax=1]的关系,图片都无法正常显示.
有知道原因的请不吝赐教.
10_03 凝聚聚类计算人脸数据
# 数据聚类_使用凝聚聚类计算人脸数据
# - 凝聚聚类
# - 聚类特点:
# - 算法需指定最终簇个数(簇个数可任意设定).
# - 需指定寻找相近值得规则.
# - 无法控制噪声
# - 簇中成员分布均匀
# 概要:
# 1. 使用人脸数据,并控制每人最多只能有50张图
# 2. 使用PCA提取人脸识别的主要成分
# 3. 查看凝聚聚类(ward 方差最小)在PCA过滤后数据上的表现
# 4. 评估Kmenas与凝聚聚类所形成簇的相似度
# 5. 重建凝聚聚类簇人脸图像
# 观察结果:
# 同Kmeans出现了同样的问题,簇的形成时基于相似度参数来完成的(使用的ward 默认值),
# 但是算法并不直到用户关心的合成是哪方面的,因此会按照自己的规则来寻找相似图片并形成簇.
# 此时如果想寻找指定特征的图片,还是得需要人工参与.
# 比Kmeans算法好的一点是,凝聚聚类算法所形成得簇,成员相似度较高,如果拿到得簇内容误差太大
# 可以增加算法中簇的个数,个数越细,精准度越高,相似度越高,当然人工抽检成本也越高.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.datasets import fetch_lfw_people
from sklearn.cluster import AgglomerativeClustering
from sklearn.cluster import KMeans
from sklearn.metrics import adjusted_rand_score
##########################
# 人脸数据
##########################
people = fetch_lfw_people(min_faces_per_person=20, resize=0.7)
image_shape = people.images[0].shape
# print(image_shape)
# 每人人脸图像采样最多50个
mask = np.zeros(people.target.shape, dtype=np.bool)
for target in np.unique(people.target):
mask[np.where(people.target == target)[0][:50]] = 1
X_people = people.data[mask]
y_people = people.target[mask]
##########################
# 人脸数据
##########################
# 这里用PCA预处理一下数据,因为pca不用考虑方向,对人脸数据识别较准确
# 而且适用的变换法可以缩减需要判断的数据源能效提升运行效率
pca = PCA(n_components=100, whiten=True, random_state=0)
pca.fit_transform(X_people)
X_pca = pca.transform(X_people)
##########################
# 凝聚聚类
##########################
agglomerative = AgglomerativeClustering(n_clusters=10)
labels_agg = agglomerative.fit_predict(X_pca)
print("Cluster sizes agglomerative clustering: {}".format(
np.bincount(labels_agg)))
# 簇的成员数分布不太均匀, 差于Kmenas, 但好于DBSCAN
# Cluster sizes agglomerative clustering: [529 376 64 114 31 39 4 66 8 41]
##########################
# 比较凝聚聚类与K均值聚类形成簇的相似度
##########################
# 聚类比较之前介绍过,在有真实值的情况下可以用 adjusted_rand_score来评估相似度
km = KMeans(n_clusters=10, random_state=0)
labels_km = km.fit_predict(X_pca)
print("ARI: {:.2f}".format(adjusted_rand_score(labels_agg, labels_km)))
# 得分很低
# 原因:
# Kmeans聚集算平均值,无差别聚集,因此原理核中心点,可能偏差很大
# 凝聚聚类每个簇中的成员都或多或少的相似,
# 因此在比较这两个簇时会出现得分很低的情况.
# ARI: 0.09
##########################
# 显示凝聚聚类找到的簇中人像
##########################
# 凝聚聚类没有像Kmeans那样的簇中心点,但是可以通过簇间接得到簇个数.
# 这里直接定义常量了,简单明了
n_clusters = 10
for cluster in range(n_clusters):
mask = labels_agg == cluster
fig, axes = plt.subplots(1, 10, subplot_kw={'xticks': (), 'yticks': ()},
figsize=(15, 8))
axes[0].set_ylabel(np.sum(mask))
for image, label, asdf, ax in zip(X_people[mask], y_people[mask],
labels_agg[mask], axes):
ax.imshow(image.reshape(image_shape))
ax.set_title(people.target_names[label].split()[-1],
fontdict={'fontsize': 9})
plt.show()
11 章节总结
- 缩放数据:
属于通用的数据预处理
| 算法 | 位置 | 概要 |
|---|---|---|
| MinMaxScaler | from sklearn.preprocessing import MinMaxScaler | 使所有特征都刚好位于0 到1 之间。 对于二维数据集来说,所有的数据都包含在x 轴0 到1 与y 轴0 到1 组成的矩形中。 |
| StandardScaler | from sklearn.preprocessing import StandardScaler | 确保每个特征的平均值为0、方差为1, 使所有特征都位于同一量级 |
| RobustScaler | from sklearn.preprocessing import RobustScaler | 与StandardScaler 类似, 确保每个特征的统计属性都位于同一范围。 但RobustScaler 使用的是中位数和四分位数1, 而不是平均值和方差。 这样RobustScaler 会忽略与其他点有很大不 同的数据点(比如测量误差) |
- 解构数据(数据变换)
属于专有的数据预处理,只能作用在训练数据上
| 算法 | 位置 | 概要 |
|---|---|---|
| PCA 主成分分析 |
from sklearn.decomposition import PCA | ・ 压缩算法 ・ 可以提取数据主要成分 ・ 不关心数据方向 ・ 只能用于训练数据" |
| NMF 非负矩阵分解 |
from sklearn.decomposition import NMF | ・ 压缩算法 ・ 可以提取数据主要成分 ・ 要求数据必须全是正值 ・ 可以保留数据方向 ・ 只能用于训练数据" |
| t-SNE 流式学习 |
from sklearn.manifold import TSNE | ・ 主要用于数据可视化 ・ 数据特征尽量不要超过2个 ・ 只能用于训练数据 ・ 主要用于探索性数据分析 |
- 聚拢数据(聚类)
| 算法 | 位置 | 概要 |
|---|---|---|
| K均值聚类 | from sklearn.cluster import Kmeans | ・ 凝聚算法 ・ 簇的个数需要预先指定 ・ 簇的个数任意指定,可以与实际不符 ・ 随机起点 ・ 有簇中心点,中心点为簇成员的平均值 ・ 簇成员为邻近选取,因此成员间可能有差别很大的情况 ・ 算法结束条件为: 无论怎样分配成员,中心点的值都不变为止 ・ 只能用于训练数据 |
| 凝聚聚类 | from sklearn.cluster import AgglomerativeClustering | ・ 凝聚算法 ・ 簇的个数需要预先指定 ・ 簇的个数任意指定,可以与实际不符 ・ 随机起点 ・ 无簇中心点 ・ 簇成员都有相似处,根据参数来指定判定相似的方式 ・ 算法结束条件为: 所有数据点都分配完且最终簇的个数与设定相符 ・ 只能用于训练数据" |
"DBSCAN 带有噪点的空间凝聚 |
from sklearn.cluster import DBSCAN | ・ 凝聚算法 ・ 不需要预先指定簇的个数 ・ 无簇中心点 ・ 簇成员仅是靠空间范围相近的原则聚拢成簇,无邻近成员就会标记成噪点,被成功标记的簇,会遍历完所有的簇成员(寻找成员的相近点)后,用同样的方法再去从新的未经标记的点开始寻找 ・ 算法结束条件为: 每个点都被标记过. ・ 只能用于训练数据 |