Spatial Transformer Networks
论文:https://arxiv.org/abs/1506.02025
1 核心思想
CNN中使用的最大池化操作,使得网络对输入图像具有了一定的平移不变性。但是,由于一般使用的池化核很小(2 x 2),因此需要使用多个最大池化层才能实现较大的平移不变性。但即便如此,网络的中间层对输入的平移不变性仍然比较小。
作者提出了一个空间变换层(Spatial Transformer Layer,STL)实现对输入的平移、缩放、旋转、裁剪等操作。STL是可微分的,可以加入到CNN中进行前向和反向传播,实现对输入feature map的变换。对于多通道的输入,是对每一个channel应用相同的变换。
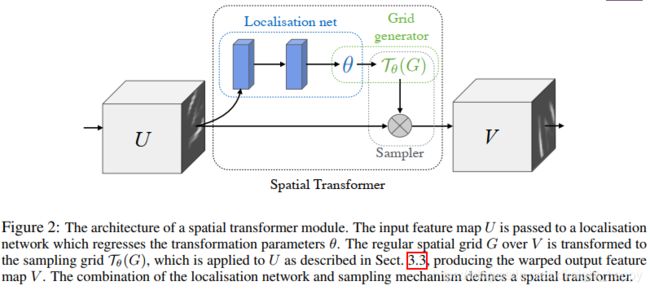
STL包含三部分,分别是定位网络(Localisation Network)、grid generator和sampler。
1.1 定位网络
定位网络的目的是学习对输入变换的参数 θ \theta θ。其输入为 U ∈ R H × W × C U \in R^{H \times W \times C} U∈RH×W×C。定位网络可以是一个小型的全连接网络,也可以是一个小型的卷积网络,但最后应该是一个回归层用于输出预测参数 θ \theta θ。
要学习的参数的数量和定义的变换的形式有关,例如,对于仿射变换,要学习的参数量即为6个。
以仿射变换为例,偏移、缩放、旋转都是对输入feature map应用线性变换。
平移:
[ x ′ y ′ 1 ] = [ 1 0 Δ x 0 1 Δ y ] [ x y 1 ] \left[\begin{matrix}x^{'} \\ y^{'} \\ 1 \end{matrix}\right] = \left[\begin{matrix}1 &&0 && \Delta x\\ 0 && 1 && \Delta y\end{matrix}\right] \left[\begin{matrix}x \\ y \\ 1 \end{matrix}\right] ⎣⎡x′y′1⎦⎤=[1001ΔxΔy]⎣⎡xy1⎦⎤
缩放:
[ x ′ y ′ 1 ] = [ s 1 0 0 0 s 2 0 ] [ x y 1 ] \left[\begin{matrix}x^{'} \\ y^{'} \\ 1 \end{matrix}\right] = \left[\begin{matrix}s_1 &&0 && 0\\ 0 && s_2 && 0\end{matrix}\right] \left[\begin{matrix}x \\ y \\ 1 \end{matrix}\right] ⎣⎡x′y′1⎦⎤=[s100s200]⎣⎡xy1⎦⎤
旋转:
[ x ′ y ′ 1 ] = [ cos θ − sin θ 0 sin θ cos θ 0 ] [ x y 1 ] \left[\begin{matrix}x^{'} \\ y^{'} \\ 1 \end{matrix}\right] = \left[\begin{matrix}\cos\theta &&-\sin\theta && 0\\ \sin\theta && \cos\theta && 0\end{matrix}\right] \left[\begin{matrix}x \\ y \\ 1 \end{matrix}\right] ⎣⎡x′y′1⎦⎤=[cosθsinθ−sinθcosθ00]⎣⎡xy1⎦⎤
1.2 grid generator
grid generator是确定输出feature map每一个点映射到输入feature map的哪个点。具体的数学变换形式为:
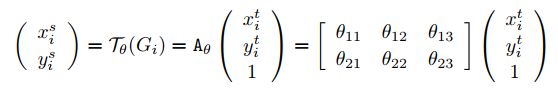 这里, ( x i t , y i t ) (x^t_i,y^t_i) (xit,yit)表示输出feature map的某个位置, ( x i s , y i s ) (x^s_i,y^s_i) (xis,yis)表示输入feature map的某个位置, A θ A_{\theta} Aθ就是变换矩阵。
这里, ( x i t , y i t ) (x^t_i,y^t_i) (xit,yit)表示输出feature map的某个位置, ( x i s , y i s ) (x^s_i,y^s_i) (xis,yis)表示输入feature map的某个位置, A θ A_{\theta} Aθ就是变换矩阵。
这里为什么要将变换矩阵应用于输出feature map而不是输入feature map?一个相对合理的解释是,输出要从输入上拿数据点,而目标是需要填满输出feature map,需要遍历输出feature map且保证其为规则的矩形。如果是对输入进行变换,那么可能造成输出是非规则的,即便我们可以使用其最小外接矩形保证其形状规则,但新添加的点的值无法确定。所以这里用输出到输入的变换,保证输出是规则的且每一个点的值是确定的。
不同形式的变换矩阵,可以实现不同的变换,如下图(a)实现恒等变换,(b)实现仿射变换。
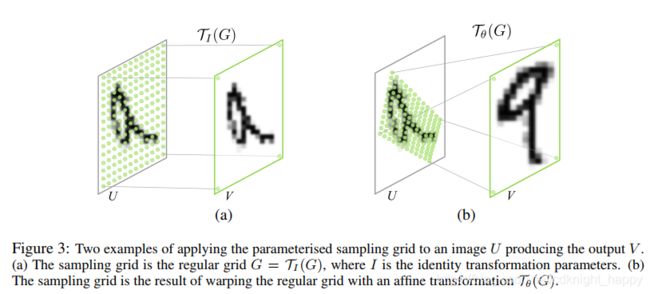 应用于图像注意力区域学习时,使用的变换矩阵可以是如下形式:
应用于图像注意力区域学习时,使用的变换矩阵可以是如下形式:
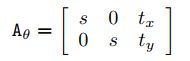
即输入是输出的缩放和平移,缩放又是对各个坐标轴同等尺度的缩放。
1.3 可微分的采样
上面求得了变换矩阵,下面就需要对输入feature map U进行采样得到输出feature map V。采样的函数可以表示成:
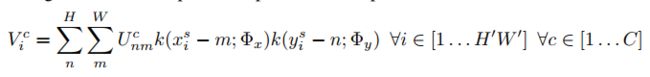 k ( ) k() k()是采样函数, Φ x , Φ y \Phi_x,\Phi_y Φx,Φy是采样函数的参数, U n m c U_{nm}^c Unmc是输入的第c个channel位置(n,m)处的值, V i c V_i^c Vic是输出的第c个channel位置 ( x i t , y i t ) (x_i^t,y_i^t) (xit,yit)处的值。采样时也是对所有的channel应用相同的操作。
k ( ) k() k()是采样函数, Φ x , Φ y \Phi_x,\Phi_y Φx,Φy是采样函数的参数, U n m c U_{nm}^c Unmc是输入的第c个channel位置(n,m)处的值, V i c V_i^c Vic是输出的第c个channel位置 ( x i t , y i t ) (x_i^t,y_i^t) (xit,yit)处的值。采样时也是对所有的channel应用相同的操作。
理论上,这里可以使用任意的采样函数,只要其对 x i s , y i s x_i^s,y_i^s xis,yis是可微的即可。以双线性差值为例,插值公式可以写作:
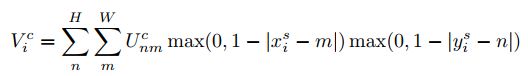 那么反向传播公式有:
那么反向传播公式有:
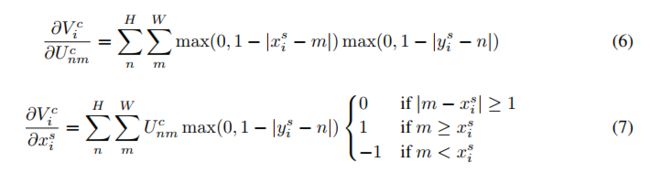 公式(6)可以看出,输出feature map对输入是可微分的,输出的feature map对采样的坐标也是可微分的,由于 ∂ x i s ∂ θ \frac{\partial x_i^s}{\partial \theta} ∂θ∂xis ∂ y i s ∂ θ \frac{\partial y_i^s}{\partial \theta} ∂θ∂yis也可以求得,那么就可以通过输出对变换参数 θ \theta θ和定位网络求梯度进行训练。
公式(6)可以看出,输出feature map对输入是可微分的,输出的feature map对采样的坐标也是可微分的,由于 ∂ x i s ∂ θ \frac{\partial x_i^s}{\partial \theta} ∂θ∂xis ∂ y i s ∂ θ \frac{\partial y_i^s}{\partial \theta} ∂θ∂yis也可以求得,那么就可以通过输出对变换参数 θ \theta θ和定位网络求梯度进行训练。
2 应用
将spatial transformer layer加入到网络中,即可实现spatial transformer network。可以对一个输入应用多个spatial transformer layer,让每个STL去学习输入中的一个感兴趣的目标,将各变换的输出进行融合即可实现对多个目标的变换。
使用STL时不需要添加额外的标注信息,使用原来的损失函数即可以让模型学习对输入的变换以取得更好的处理结果。

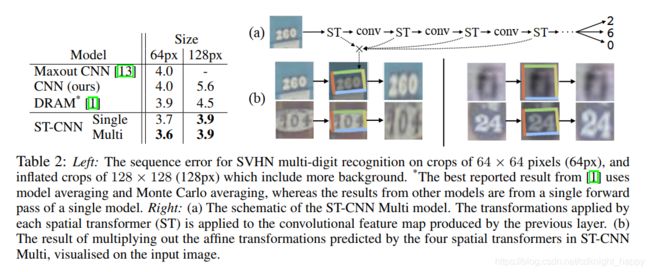
 应用于分类的时候,可以使用STL对输入进行变换,规范化其形状之后有助于分类。应用于细粒度分类时,可以使用STL作为一种注意力机制,使用多个STL去挖掘图像中多个感兴趣的目标区域。
应用于分类的时候,可以使用STL对输入进行变换,规范化其形状之后有助于分类。应用于细粒度分类时,可以使用STL作为一种注意力机制,使用多个STL去挖掘图像中多个感兴趣的目标区域。
3 pytorch实现代码
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(1, 10, kernel_size=5)
self.conv2 = nn.Conv2d(10, 20, kernel_size=5)
self.conv2_drop = nn.Dropout2d()
self.fc1 = nn.Linear(320, 50)
self.fc2 = nn.Linear(50, 10)
# Spatial transformer localization-network
self.localization = nn.Sequential(
nn.Conv2d(1, 8, kernel_size=7),
nn.MaxPool2d(2, stride=2),
nn.ReLU(True),
nn.Conv2d(8, 10, kernel_size=5),
nn.MaxPool2d(2, stride=2),
nn.ReLU(True)
)
# Regressor for the 3 * 2 affine matrix
self.fc_loc = nn.Sequential(
nn.Linear(10 * 3 * 3, 32),
nn.ReLU(True),
nn.Linear(32, 3 * 2)
)
# Initialize the weights/bias with identity transformation
self.fc_loc[2].weight.data.zero_()
self.fc_loc[2].bias.data.copy_(torch.tensor([1, 0, 0, 0, 1, 0], dtype=torch.float))
# Spatial transformer network forward function
def stn(self, x):
xs = self.localization(x)
xs = xs.view(-1, 10 * 3 * 3)
theta = self.fc_loc(xs)
theta = theta.view(-1, 2, 3)
grid = F.affine_grid(theta, x.size())
x = F.grid_sample(x, grid)
return x
def forward(self, x):
# transform the input
x = self.stn(x)
# Perform the usual forward pass
x = F.relu(F.max_pool2d(self.conv1(x), 2))
x = F.relu(F.max_pool2d(self.conv2_drop(self.conv2(x)), 2))
x = x.view(-1, 320)
x = F.relu(self.fc1(x))
x = F.dropout(x, training=self.training)
x = self.fc2(x)
return F.log_softmax(x, dim=1)
三个关键点:
- 定位网络最后一层是Linear层;
- torch.nn.functional.affine_grid(theta,x.size())得到变换后的target的坐标;
- torch.nn.functional.grid_sample(x,grid)得到插值的结果。
参考:
https://blog.csdn.net/qq_39422642/article/details/78870629
https://www.jianshu.com/p/723af68beb2e
https://blog.csdn.net/xholes/article/details/80457210