SMOKE: Single-Stage Monocular 3D Object Detection via Keypoint Estimation 论文笔记
SMOKE: Single-Stage Monocular 3D Object Detection via Keypoint Estimation 论文笔记
论文链接: https://arxiv.org/abs/2002.10111

一、 Problem Statement
目前的单目3D视觉中,通常非常依赖于RCNN网络或者RPN网络,然后会多加一个分支去学习3D信息或者产生伪激光雷达,然后将它们放入点云检测网络中。作者认为2D检测网络是冗余的,且对3D目标检测来说引入了不可忽视的噪声,导致学习3D几何信息困难。作者且认为,如果3D信息和相机内参矩阵已经知道,2D信息可以很自然地得到。
二、 Direction
提出了一个multi-step disentangling(to separate different ideas or pieces of information that have become confused together) 的方法, 即消除2D检测分支,添加一个3D回归分支,直接在图片上预测3D点,也就是一个关键点和3D变量组成3D bounding box。
三、 Method
所谓的单目3D目标检测问题,可以认为是:给定了一个RGB图像 I ∈ R W × H × 3 I \in \R^{W \times H \times 3} I∈RW×H×3,找到类别 C C C和3D Bounding Box,后者可以表达为 ( h , w , l , x , y , z , θ ) (h,w,l,x,y,z,\theta) (h,w,l,x,y,z,θ)。

由上图可以知道,SMOKE分为三个部分:
- Backbone
- 3D detection
- Loss function
1. Backbone

作者使用了DLA-34作为Backbone,其可以融合不同层之间的信息。但作者做了一些修改:
-
使用Deformable Convolution Network替换所有的hierarchical aggregation connections。
-
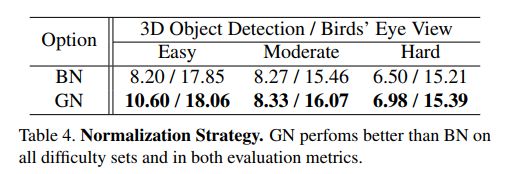
使用GN层替换所有的BN层。(对Batch Size less sensitive且对training noise更加鲁棒)

-
输出特征图是相对于输入图像的4倍下采样。
2. 3D 检测网络
检测网络总共有两个分支:
- Keypoint Branch
- Regression Branch
(1) Keypoint Branch
这一部分和CenterNet相似,也就是将目标用一个点表示。但这里不是检测2D Bounding Box的中心点,而是将目标的3D中心映射到2D平面。 如下图所示:

作者这样做的目的是因为投影的点能够很好的恢复3D位置。假设 [ x , y , z ] T [x,y,z]^T [x,y,z]T是每个目标的3D中心,那么投影到2D平面的3D点为 [ x c , y c ] T [x_c, y_c]^T [xc,yc]T,这是由相机内参矩阵 K K K得到的:
[ z ⋅ x c z ⋅ y c z ] = K 3 × 3 [ x y z ] \bigg[ \begin{aligned} z &\cdot x_c \\ z &\cdot y_c \\ &z \end{aligned} \bigg] = K_{3\times 3} \bigg[\begin{aligned} x \\ y\\ z \end{aligned}\bigg] [zz⋅xc⋅ycz]=K3×3[xyz]
每个点对应的ground-truth keypoint,就是它们下采样后特征图中的位置,然后使用Gaussian Kernel分布。每一个在图像上的3D点都是由8个2D点所对应 [ x b , 1 ∼ 8 , y b , 1 ∼ 8 ] T [x_{b,1\sim 8}, y_{b, 1\sim 8}]^T [xb,1∼8,yb,1∼8]T,且标准差通过包围3D Box的最小2D box { x b m i n , y b m i n , x b m a x , y b m a x } \{x_b^{min}, y_b^{min}, x_b^{max}, y_b^{max}\} {xbmin,ybmin,xbmax,ybmax}计算。
(2) Regression Branch
作者对每一个在heatmap上的关键点预测了一个8维度的变量来构建3D Bounding Box, τ = [ δ z , δ x e , δ y e , δ h , δ w , δ l , sin α , cos α ] T \tau = [\delta_z, \delta_{x_e},\delta_{y_e},\delta_h, \delta_w, \delta_l, \sin \alpha , \cos \alpha]^T τ=[δz,δxe,δye,δh,δw,δl,sinα,cosα]T。其中, δ z \delta_z δz表示深度的偏差; δ x e , δ y e \delta_{x_e},\delta_{y_e} δxe,δye表示下采样导致的离散化偏差; δ h , δ w , δ l \delta_h, \delta_w, \delta_l δh,δw,δl表示边的维度; sin α , cos α \sin \alpha , \cos \alpha sinα,cosα是偏航角 α \alpha α的矢量表示。因此,回归的大小是 S r ∈ R H R × W H × 8 S_r \in \R^{\frac{H}{R} \times \frac{W}{H}\times 8} Sr∈RRH×HW×8 。收到lifting transformation的启发,作者引入了类似的变换 F F F,用来转换投影的3D点到3D Bounding Box
B = F ( τ ) ∈ R 3 × 8 B = F(\tau) \in \R^{3 \times 8} B=F(τ)∈R3×8
对于深度 z z z,它是由预先定义的尺度和偏移参数 σ z , μ z \sigma_z, \mu_z σz,μz计算得到的:
z = μ z + δ z σ z z = \mu_z + \delta_z \sigma_z z=μz+δzσz
所以,有了深度 z z z之后,与它投影的中心 [ x c , y c ] T [x_c, y_c]^T [xc,yc]T和下采样偏差 [ δ x e , δ y e ] [\delta_{x_e},\delta_{y_e}] [δxe,δye]相结合,就可以得到3D坐标点:
[ x y z ] = K 3 × 3 − 1 [ z ⋅ ( x c + δ x e ) z ⋅ ( y c + δ y e ) z ] \bigg[\begin{aligned} x \\ y\\ z \end{aligned}\bigg] = K_{3\times 3}^{-1} \bigg[\begin{aligned} z &\cdot (x_c+ \delta_{x_e})\\ z &\cdot (y_c+\delta_{y_e}) \\ &z \end{aligned}\bigg] [xyz]=K3×3−1[zz⋅(xc+δxe)⋅(yc+δye)z]
而3D Bounding Box的长宽高, [ h , w , l ] [h, w, l] [h,w,l],作者使用预先计算好整个数据集的category-wise average dimension [ h ˉ , w ˉ , l ˉ ] [\bar{h}, \bar{w}, \bar{l}] [hˉ,wˉ,lˉ]来计算。
[ h w l ] = [ h ˉ ⋅ e δ h w ˉ ⋅ e δ w l ˉ ⋅ e δ l ] \bigg[\begin{aligned} h \\ w\\ l \end{aligned}\bigg] = \bigg[\begin{aligned} \bar{h} \cdot e^{\delta_h} \\ \bar{w} \cdot e^{\delta_w} \\ \bar{l} \cdot e^{\delta_l} \end{aligned}\bigg] [hwl]=[hˉ⋅eδhwˉ⋅eδwlˉ⋅eδl]
我们选择回归观测角度 α \alpha α,而不是偏航角 θ \theta θ。

所以,偏航角为:
θ = α z + arctan ( x z ) \theta = \alpha_z + \arctan (\frac{x}{z}) θ=αz+arctan(zx)
最后3D Bounding Box的8个角点为:
B = R θ [ ± h / 2 ± w / 2 ± l / 2 ] + [ x y z ] B = R_{\theta} \bigg[ \begin{aligned} \plusmn h/2 \\ \plusmn w/2 \\ \plusmn l/2 \end{aligned} \bigg] + \bigg[ \begin{aligned} x \\ y \\ z \end{aligned} \bigg] B=Rθ[±h/2±w/2±l/2]+[xyz]
3. 损失函数
整体的Loss Function为:
L = L c l s + ∑ i = 1 3 L r e g ( B ^ i ) L = L_{cls} + \sum_{i=1}^3 L_{reg}(\hat{B}_i) L=Lcls+i=1∑3Lreg(B^i)
(1) Keypoint Classification Loss
这一部分使用的是penality-reduced focal loss。可以从网络框架图中看到,粉红色的大小为: H 4 × W 4 × C \frac{H}{4} \times \frac{W}{4} \times C 4H×4W×C,其中 C C C代表C个类别,也就是每个类别有一个keypoint loss。假设 s i , j s_{i,j} si,j是heatmap中位置 ( i , j ) (i,j) (i,j)预测的值,然后 y i , j y_{i,j} yi,j为Gaussian Kernel中每个点的ground-truth值。
y ^ i , j = { 0 , i f y i , j = 1 y i , j , o t h e r w i s e , s ^ i , j = { s i , j , i f y i , j = 1 1 − s i , j , o t h e r w i s e \hat{y}_{i,j} = \bigg \{ \begin{aligned} &0, \qquad if \quad y_{i,j} =1 \\ &y_{i,j}, \quad otherwise \end{aligned} , \quad \hat{s}_{i,j} = \bigg \{ \begin{aligned} &s_{i,j}, \qquad if \quad y_{i,j} =1 \\ &1-s_{i,j}, \quad otherwise \end{aligned} y^i,j={0,ifyi,j=1yi,j,otherwise,s^i,j={si,j,ifyi,j=11−si,j,otherwise
因此,分类损失为:
L c l s = − 1 N ∑ i , j = 1 h , w ( 1 − y ^ i , j ) β ( 1 − s ^ i , j ) α log ( s ^ i , j ) L_{cls} = -\frac{1}{N} \sum_{i,j=1}^{h,w}(1-\hat{y}_{i,j})^{\beta}(1-\hat{s}_{i,j})^{\alpha} \log(\hat{s}_{i,j}) Lcls=−N1i,j=1∑h,w(1−y^i,j)β(1−s^i,j)αlog(s^i,j)
其中, N N N是每张图片中关键点的数量。 ( 1 − y i , j ) (1-y_{i,j}) (1−yi,j)对应于点ground truth位置的penalty reduction。
(2) Regression Loss
作者在每个feature map位置上对回归的尺度和角度参数添加了channel-wise activation,用来保持一致性。激活函数选择sigmoid function σ \sigma σ和使用了L2 Norm。
[ δ h δ w δ l ] = σ ( [ o h o w o l ] ) − 1 2 , [ sin α cos α ] = [ o sin / o s i n 2 + o c o s 2 o cos / o s i n 2 + o c o s 2 ] \bigg[ \begin{aligned} \delta_h \\ \delta_w \\ \delta_l \end{aligned} \bigg] = \sigma \bigg( \begin{aligned} \bigg[ \begin{aligned} o_h \\ o_w \\ o_l \end{aligned} \bigg] \end{aligned}\bigg) - \frac{1}{2}, \bigg[ \begin{aligned} \sin \alpha \\ \cos \alpha \end{aligned}\bigg] = \bigg[ \begin{aligned} o_{\sin} / \sqrt{o^2_{sin} + o^2_{cos}} \\ o_{\cos} / \sqrt{o^2_{sin} + o^2_{cos}} \end{aligned}\bigg] [δhδwδl]=σ([ohowol])−21,[sinαcosα]=[osin/osin2+ocos2ocos/osin2+ocos2]
这里的 o o o 表示网络的输出。使用L1 distance来作为3D bounding box regression loss。
L r e g = λ N ∣ ∣ B ^ − B ∣ ∣ 1 L_{reg} = \frac{\lambda}{N} ||\hat{B} - B||_1 Lreg=Nλ∣∣B^−B∣∣1
这里的 B ^ \hat{B} B^是预测的变换, B B B为ground-truth。
四、性能表现


五、 Conclusion
简单的单目3D目标检测,用在了新版本的APOLLO上。直接回归3D参数,没有通过2D Bounding Box。在构造回归分支的损失函数时,将多个属性对损失函数的贡献解耦,加速模型收敛。速度较快。
百度在Apollo7.0中也基于SMOKE框架开发出了一个新的基于视觉的障碍物检测模型,其针对SMOKE做了一些改进,并在waymo数据集上进行了训练和测试。改进点:
- 使用常规卷积替换可变性卷积,从而能转换为onnx或libtorch,便于模型部署;
- 增加了一个用于预测2D边界框中心点与3D边界框中心点投影之间的偏移量的head,然后将该偏移量与2D边界框中心点相加来替换- 原有的3D边界框中心点投影预测,以应对部分截断障碍物的3D中心点投影出现在图像以外区域,以至于被过滤掉的问题;
- 原有的SMOKE框架没有预测2D边界框,Apollo在部署的时候仍然加入了2D边界框的预测。通过预测2D边框的中心点、宽度和高度,计算出障碍物的2D边框。
六、 Reference
- https://mp.weixin.qq.com/s/ZEI_gBM847QkzLmas-E5iQ