【机器学习】ID3_C4.5_CART算法总结与对比

问题

ID3、C4.5、CART算法总结与对比

前言

ID3、C4.5、CART算法是三种不同的决策树算法，区别主要在最优划分属性的选择上，下面把之前在随机森林中汇总过的复制过来，然后再总结下三者的不同。

三种算法所用的最优属性选择方法详述

信息增益 (ID3决策树中采用)

**“信息熵”**是度量样本集合纯度最常用的一种指标，假定当前样本结合 $D$ 中第 $k$ 类样本所占的比例为 $p_k(k=1,2,...,c)$ ，则 $D$ 的信息熵定义为：
$$Ent(D)=-\sum _{k=1}^c{p}_{k}lo{g}_2{p}_k$$
$Ent(D)$ 的值越小，则 $D$ 的纯度越高。注意因为 $p_k\le 1$ ，因此 $Ent(D)$ 也是一个大于等于０小于１的值。

假定离散属性 $a$​​​​ 有 V 个可能的取值 $\{a^1,a^2,...,a^V\}$​​​​ ，若使用 $a$​​​​ 来对样本集合 $D$​​​​ 进行划分的话，则会产生 V 个分支结点，其中第 $v$​​​​ 个分支结点包含了 $D$​​​​ 中所有在属性 $a$​​​​ 上取值为 $a^v$​​​​ 的样本，记为 $D^v$​​​​ 。同样可以根据上式计算出 $D^v$​​​​ 的信息熵，再考虑到不同的分支结点所包含的样本数不同，给分支结点赋予权重 $\frac{|D^v|}{|D|}$​​​​ ，即样本数越多的分支结点的影响越大，于是可以计算出使用属性 $a$​​​​ 对样本集 $D$​​​​​ 进行划分时所获得的“信息增益”：
即：对于属性a，求出其各个取值下的信息熵，然后再以各个取值下样本的数目为权重，求出所有取值的信息熵加权和作为以该属性对应的信息熵——>用划分之前的信息熵-当前属性的信息熵=当前属性对应的信息增益。越大说明该属性划分效果越好。
$$Gain(D,a)=Ent(D)-\sum _{v=1}^V\frac{|D^v|}{|D|}Ent(D^v)$$
一般而言，信息增益越大越好，因为其代表着选择该属性进行划分所带来的纯度提升，因此全部计算当前样本集合 $D$ 中存在不同取值的那些属性的信息增益后，取信息增益最大的那个所对应的属性作为划分属性即可。

**缺点：**对可取值数目多的属性有所偏好（分的越细，每个子类的信息熵越小，总的信息增益就越大）

增益率 (C4.5决策树中采用)

从信息增益的表达式很容易看出，信息增益准则对可取值数目多的属性有所偏好，为减少这种偏好带来的影响，大佬们提出了增益率准则，定义如下：
$$\begin{gathered} Gain\_ratio(D,a)=\frac{Gain(D,a)}{IV(a)} \\ IV(a)=-\sum _{v=1}^V\frac{|D^v|}{|D|}lo{g}_2\frac{|D^v|}{|D|} \end{gathered}$$
$IV(a)$​​ 称为属性 a 的“固有值”。属性 a 的可能取值数目越多，则 $IV(a)$​​​ 的值通常会越大，因此一定程度上抵消了信息增益对可取值数目多的属性的偏好。
即：在信息增益的基础上除以一个与属性取值数量相关的值，这个值就是属性的信息熵，属性取值越多，熵越大（类比一个数据中类别越多，熵越大）

注意：$IV(a)$并不是$Ent(D)$，后者是类别的信息熵，前者是特征的信息熵（特征可取范围越多，熵越大）

**缺点：**增益率对可取值数目少的属性有所偏好

因为增益率存在以上缺点，因此C4.5算法并不是直接选择增益率最大的候选划分属性，而是使用了一个启发式：先从候选划分属性中找出信息增益高于平均水平的属性，再从中选择增益率最高的。

基尼指数 (CART决策树中采用)

ID3中根据属性值分割数据，之后该特征不会再起作用，这种快速切割的方式会影响算法的准确率，因为这是种贪心算法，不能保证找到全局最优值。CART是一棵二叉树，采用二元切分法，每次把数据切成两份，分别进入左子树、右子树。而且每个非叶子节点都有两个孩子，所以CART的叶子节点比非叶子多1。相比ID3和C4.5，CART应用要多一些，既可以用于分类也可以用于回归。

这里改用基尼值来度量数据集 $D$ 的纯度，而不是上面的信息熵。基尼值定义如下：
$$Gini(D)=\sum _{k=1}^c{p}_k(1-p_k)=1-\sum _{k=1}^c{p}_k^2=1-\sum _{k=1}^c(\frac{D^k}{D}{)}^2$$
直观来看，$Gini(D)$ 反映了从数据集 $D$ 中随机抽取两个样本，其类别标记不一致的概率，因此$Gini(D)$ 越小，则数据集 $D$ 的纯度越高。

对于样本D，个数为|D|，根据特征A的某个值a，把D分成|D1|和|D2|，则在特征A的条件下，样本D的基尼系数表达式为：
$$Gini\_index(D,A)=\frac{|D^1|}{|D|}Gini(D^1)+\frac{|D^2|}{|D|}Gini(D^2)$$
于是，我们在候选属性集合A中，选择那个使得划分后基尼系数最小的属性作为最优划分属性即可。

三种算法对比总结

下面是根据自己的理解整理的，不知道全不全，应该差不多了。

ID.3

1. 最优划分属性选择方法：信息增益
2. 分支数：可多分支
3. 能否处理连续值特征：不能
4. 缺点：偏好与可取值数目多的属性
   1. ID3算法没有进行决策树剪枝，容易发生过拟合
   2. ID3算法没有给出处理连续数据的方法，只能处理离散特征
   3. ID3算法不能处理带有缺失值的数据集,需对数据集中的缺失值进行预处理
   4. 信息增益准则对可取值数目较多的特征有所偏好(信息增益反映的给定一个条件以后不确定性减少的程度,必然是分得越细的数据集确定性更高,也就是条件熵越小,信息增益越大)

C4.5

1. 最优划分属性选择方法：增益率
2. 分支数：可多分支
3. 能否处理连续值特征：能，C4.5 决策树算法采用的二分法机制来处理连续属性。对于连续属性 a，首先将 n 个不同取值进行从小到大排序，选择相邻 a 属性值的平均值 t 作为候选划分点，划分点将数据集分为两类，因此有包含 n－1 个候选划分点的集合，分别计算出每个划分点下的信息增益，选择信息增益最大对应的划分点，仍然以信息增益最大的属性作为分支属性。
   不同于离散属性，如果当前节点划分属性为连续属性，其后代节点依然可以以该连续属性进行属性划分。
4. 缺点：增益率对可取值数目少的属性有所偏好，因此C4.5算法并不是直接选择增益率最大的候选划分属性，而是使用了一个启发式：先从候选划分属性中找出信息增益高于平均水平的属性，再从中选择增益率最高的。
5. 采用后剪枝。

CART

1. 最优划分属性选择方法：基尼系数
2. 分支数：二叉树
3. 能否处理连续值特征：能，做法与C4.5一样。也可以用于回归，用于回归时通过最小化均方差能够找到最靠谱的分枝依据，回归树的具体做法可见机器学习的问题33。
4. 优点：与ID3、C4.5不同，在ID3或C4.5的一颗子树中，离散特征只会参与一次节点的建立，但是在CART中之前处理过的属性在后面还可以参与子节点的产生选择过程。

缺失值处理

CART 算法使用一种惩罚机制来抑制提升值，从而反映缺失值的影响。为树的每个节点都找到代理分裂器，当 CART 树中遇到缺失值时，这个实例划分到左边还是右边是决定于其排名最高的代理，如果这个代理的值也缺失了，那么就使用排名第二的代理，以此类推，如果所有代理值都缺失，那么默认规则就是把样本划分到较大的那个子节点。

总结对比表

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-KuKMXKcd-1672230851003)(null)]

举例说明三个最优属性选择方法(self)

数据集示意图

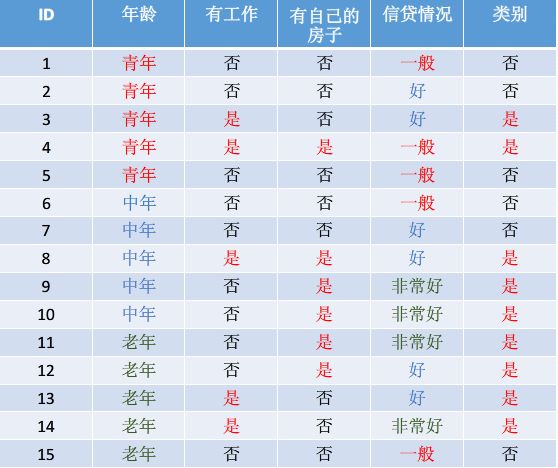
已知15个样本，两类分别6个和9个

年龄有三个取值：第一取值有5个样本，两类分别为3，2；第二个取值有5个样本，两类分别为2，3；第三个取值有5个样本，两类分别为1，4

ID3

信息增益=信息熵-条件熵（也可以说是 划分前的信息熵-划分后的信息熵）

信息熵：总的数据集下输出类别Y的信息熵。
$$H(Y)=-(\frac{6}{15}\log \frac{6}{15}+\frac{9}{15}\log \frac{9}{15})=0.971$$
**条件熵（划分后的信息熵）：**将所有训练样本按照该属性(X)划分到多个子集中，所有子集信息熵的加权和就是条件熵
$$\begin{array}{rl}以年龄(X)属性划分：& \\ 第一个子集的Y信息熵：& H(Y|X=1)=-(\frac{3}{5}\log \frac{3}{5}+\frac{2}{5}\log \frac{2}{5})=0.971\\ 第二个子集的Y信息熵：& H(Y|X=2)=-(\frac{2}{5}\log \frac{2}{5}+\frac{3}{5}\log \frac{3}{5})=0.971\\ 第三个子集的Y信息熵：& H(Y|X=3)=-(\frac{1}{5}\log \frac{1}{5}+\frac{4}{5}\log \frac{4}{5})=0.722\\ 总的条件熵：& H(Y|X)=\frac{1}{5}\ast H(Y|X=1)+\frac{1}{5}\ast H(Y|X=2)+\frac{1}{5}\ast H(Y|X=3)=0.888\end{array}$$
信息增益：按照特征X划分训练集前后，类别Y的信息不确定性减少的程度（官方表达：特征X对样本类别的信息增益）
$$Gain(Y,X)=H(Y)-H(Y|X)=0.083$$

C4.5

增益率的计算

增加了一个对选取特征X的信息熵计算。

年龄特征X的信息熵为：
$$H(X)=-(\frac{5}{15}\log \frac{5}{15}+\frac{5}{15}\log \frac{5}{15}+\frac{5}{15}\log \frac{5}{15})=1.585$$
该特征X的信息熵的含义为：如果该特征分的越细，说明该特征熵越大，那么该特征对类别Y的信息增益的惩罚越大。从而解决ID3趋向于分的细的特征。

所以年龄X对类别的信息增益率为：
$$Gain\_ratio(Y,X)=\frac{Gain(Y,X)}{H(X)}=\frac{0.083}{1.585}=0.052$$

CART

基尼系数的计算

总数据集下类别Y的基尼系数为:
$$Gini(Y)=1-({\frac{6}{15}}^2+{\frac{9}{15}}^2)=0.48$$
年龄特征下的基尼系数为：
$$\begin{gathered} Gini(Y,X=1)=\frac{5}{15}(1-{\frac{2}{5}}^2+{\frac{3}{5}}^2)+\frac{10}{15}(1-{\frac{3}{10}}^2+{\frac{7}{10}}^2) \\ Gini(Y,X=2)=\frac{5}{15}(1-{\frac{2}{5}}^2+{\frac{3}{5}}^2)+\frac{10}{15}(1-{\frac{4}{10}}^2+{\frac{6}{10}}^2) \\ Gini(Y,X=3)=\frac{5}{15}(1-{\frac{1}{5}}^2+{\frac{4}{5}}^2)+\frac{10}{15}(1-{\frac{5}{10}}^2+{\frac{5}{10}}^2) \\ 特征X的总基尼系数：Gini(Y,X)=\frac{1}{5}\ast Gini(Y,X=1)+\frac{1}{5}\ast Gini(Y,X=2)+\frac{1}{5}\ast Gini(Y,X=3) \\ (\text{CART因为是二叉树，所以并不会使用总的基尼系数}) \end{gathered}$$
基尼系数和信息熵都表示样本的不确定度，因此用哪个都可以，CART中用的是基尼系数

相比信息熵的优点：

1. 二次运算比熵的对数运算更加简单
2. 基尼系数和熵的误差曲线近似，因此可以用基尼系数替代熵

CART对离散值和连续值的处理方法

对于离散值

注意：这里（上面的CART基尼计算小节）只是显示了如何计算基尼系数，但实际CART并不是这样分为三个分支，而是认为处理为二叉树的形式，具体如下：

计算（青年或老年、中年）（青年或中年、老年）（中年或老年、青年）三种分割方法，并选择基尼系数最小对应的划分方式作为当前的结点。

对于连续值

同C4.5，直接遍历所有划分点计算各自的基尼系数即可。

参考链接

CART分类回归_对离散型和连续型特征列的选择

CART分类树算法具体流程

CART分类树建立算法流程，之所以加上建立，是因为CART分类树算法有剪枝算法流程。

算法输入：训练集D，基尼系数的阈值，样本个数阈值

算法输出：决策树T。

算法从根节点开始，用训练集递归建立CART分类树。

1. 对于当前节点的数据集为D，如果样本个数小于阈值或没有特征，则返回决策子树，当前节点停止递归。
2. 计算样本集D的基尼系数，如果基尼系数小于阈值，则返回决策树子树，当前节点停止递归。
3. 计算当前节点现有的各个特征的各个特征值对数据集D的基尼系数，对于离散值和连续值的处理方法和基尼系数的计算见第二节。缺失值的处理方法和C4.5算法里描述的相同。
4. 在计算出来的各个特征的各个特征值对数据集D的基尼系数中，选择基尼系数最小的特征A和对应的特征值a。根据这个最优特征和最优特征值，把数据集划分成两部分D1和D2，同时建立当前节点的左右节点，做节点的数据集D为D1，右节点的数据集D为D2。
5. 对左右的子节点递归的调用1-4步，生成决策树。

对生成的决策树做预测的时候，假如测试集里的样本A落到了某个叶子节点，而节点里有多个训练样本。则对于A的类别预测采用的是这个叶子节点里概率最大的类别。

CART回归树

决策树不仅可以用于分类问题，同样可以应用于回归问题。

回归树总体流程与分类树类似，不过在每个节点（不一定是叶子节点）都会得一个预测值，以年龄为例，该预测值等于属于这个节点的所有人年龄的平均值。分枝时穷举每一个feature的每个阈值找最好的分割点，但衡量最好的标准不再是最大熵，而是最小化均方差–即（每个人的年龄-预测年龄）^2 的总和 / N，或者说是每个人的预测误差平方和 除以 N。这很好理解，被预测出错的人数越多，错的越离谱，均方差就越大，通过最小化均方差能够找到最靠谱的分枝依据。

分枝直到每个叶子节点上人的年龄都唯一（这太难了）或者达到预设的终止条件（如叶子个数上限），若最终叶子节点上人的年龄不唯一，则以该节点上所有人的平均年龄做为该叶子节点的预测年龄。

决策树基础点

决策树的学习过程包括：特征选择、决策树生成、决策树剪枝。

决策树算法的优缺点

优点

1）简单直观，生成的决策树很直观。

2）基本不需要预处理，不需要提前归一化，处理缺失值。

3）使用决策树预测的代价是$O(lo{g}_{2}m)$。 m为样本数。

4）既可以处理离散值也可以处理连续值。很多算法只是专注于离散值或者连续值。

5）可以处理多维度输出的分类问题。

6）相比于神经网络之类的黑盒分类模型，决策树在逻辑上可以得到很好的解释。

7）可以交叉验证的剪枝来选择模型，从而提高泛化能力。

8） 对于异常点的容错能力好，健壮性高。

9）对缺失值不敏感

缺点

1）决策树算法非常容易过拟合，导致泛化能力不强。可以通过设置节点最少样本数量和限制决策树深度来改进。

2）决策树会因为样本发生一点点的改动，就会导致树结构的剧烈改变。这个可以通过集成学习之类的方法解决。

3）寻找最优的决策树是一个NP难的问题，我们一般是通过启发式方法，容易陷入局部最优。可以通过集成学习之类的方法来改善。

4）有些比较复杂的关系，决策树很难学习，比如异或。这个就没有办法了，一般这种关系可以换神经网络分类方法来解决。

5）如果某些特征的样本数量占比过大，生成决策树容易偏向于这些特征。这个可以通过调节样本权重来改善。

参考资料

决策树原理详解——举例说明三种数特征选择的方法，很好理解

决策树算法实例讲解——公式与本节的相同，且介绍的比本文清晰

决策树算法原理 (CART决策树)——举例介绍了CART建立的流程，很好理解

决策树学习笔记（三）：CART算法，决策树总结——还没仔细看，貌似和上面讲的一样

《机器学习》周志华