【机器学习】PCA算法原理

PCA算法原理

主成分分析（Components Analysis，PCA）是机器学习中最经典的降维方法，也是面试中的家常便饭，因而有必要认真梳理一遍PCA的原理，甚至需要手动推导一遍。

数据降维

在理解PCA的概念之前，我们先来认识一下什么是数据降维。降维就是用低维度的向量来表示原始高维度的特征。

例如：三维空间中分布在同一个平面上的一些点，用x,y,z三个轴来表示，就需要三个维度；而实际上，因为这些点是分布在一个平面上的，所以可以通过坐标系的旋转变换使得只需要x,y两个轴来表示这些点的数据关系，而且不会有任何损失，从而达到数据降维的目的。

降维的作用： 1.增大样本密度，可以缓解维数灾难

​ 2.减小计算开销

​ 3.去噪

PCA概念

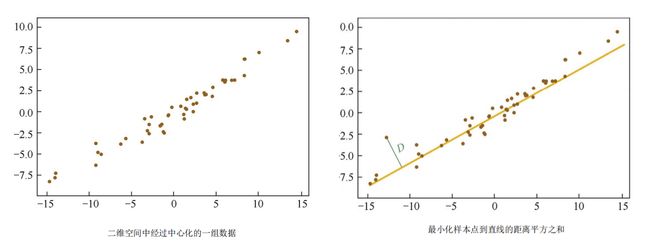
PCA是数据降维的一种方式，旨在找到数据中的主成分，并利用这些主成分来表征原始数据。简单地说，就是将n维的特征映射到k维上（k

用周志华的《机器学习》书上的话来理解就是：对于正交特征空间中的样本点，如何用一个超平面（直线的高维推广）来对所有的样本进行恰当的表达？如果存在这样的超平面（我的理解就是由k维特征重构出的主成分），那么它应该具有这样的性质：

①最大可分性：样本点在这个超平面上的投影尽可能的分开（最大化方差）

②最近重构性：样本点到这个超平面的距离都足够近（最小化平方误差）

如何理解最大可分性（最大方差）和最近重构性（最小平方误差）这两种性质呢？以及怎样才能找到这个k维的主成分呢？下面分别展开分析：

PCA之最大可分性（最大方差）

在信号处理中认为，信号具有较大的方差，噪声具有较小的方差，两者的比值称之为信噪比。信噪比越大意味着数据的质量越好，因此，我们很容易想到PCA的优化目标，就是最大化投影方差。换种说法就是，让数据在某个超平面（主轴）上投影的方差最大。

理解了最大方差的含义和PCA的优化目标，接下来将是具体的公式推导。

最大化方差公式推导

①给定一组样本点$\{v_1,v_2,...,v_n\}$，首先将其中心化后表示为$\{x_1,x_2,...,x_n\}=\{v_1-\mu ,v_2-\mu ,...,v_n-\mu \}$，其中，$\mu =\frac{1}{n}{\sum }_{i=1}^n{v}_i$。

②因为一个向量$x_i$在$\omega$（单位方向向量）上的投影可以表示为两者的内积$<x_i,\omega >=x_i^T\omega$，而PCA的目标就是找到一个投影方向$\omega$，使得所有的数据$\{x_1,x_2,...,x_n\}$在$\omega$上的投影方差尽可能地大，因此：

③投影后的方差可以表示为：
$$\begin{gathered} D(x)=\frac{1}{n}\sum _{i=1}^n(x_i^T\omega {)}^2 \\ =\frac{1}{n}\sum _{i=1}^n(x_i^T\omega {)}^T(x_i^T\omega ) \\ =\frac{1}{n}\sum _{i=1}^n{\omega }^T{x}_i{x}_i^T\omega ={\omega }^T\left(\frac{1}{n}\sum _{i=1}^n{x}_i{x}_i^T\right)\omega \end{gathered}$$
④然后可以发现，上面大括号内的$\frac{1}{n}{\sum }_{i=1}^n{x}_i{x}_i^T$就是原始样本的协方差矩阵，令其等于$\Sigma$​。

补充理解：协方差公式形式：
$$Cov(x,y)=\frac{1}{n-1}\sum _{i=1}^n(x_i-{\mu }_x)(y_i-{\mu }_y)$$
在均值 $\mu =0$ 时，（当n足够大时，n-1可以约等于n），于是有：
$$Cov(x,y)=\frac{1}{n}\sum _{i=1}^n{x}_i{y}_i$$
对于步骤③中 $x_i$，是原始样本 $v_i$ 中心化后的，因此可以说 $\frac{1}{n}{\sum }_{i=1}^n{x}_i{x}_i^T$ 就是原始样本的协方差矩阵。

⑤因此，上面的最大化方差D(x)的优化问题可以转化为
$$\begin{gathered} \{\begin{array}{l}max\{{\omega }^T\Sigma \omega \},\\ s.t.{\omega }^T\omega =1.\end{array} \\ 其中，\omega 是单位向量，因此有{\omega }^T\omega =1. \end{gathered}$$

⑥对于上面的优化目标，可以构造拉格朗日函数来解决：
$$\begin{gathered} L(\omega )={\omega }^T\Sigma \omega +\lambda (1-{\omega }^T\omega ) \\ 对\omega 求导并令其等于0，可得\Sigma \omega =\lambda \omega \end{gathered}$$

补充一点矩阵微分的知识，有助于理解上式的求导过程：（非常有用的公式！！！可以记住！）
$$\begin{gathered} ①\frac{\partial x^{T}a}{\partial x}=\frac{\partial a^{T}x}{\partial x}=a \\ ②\frac{\partial x^{T}Ax}{\partial x}=(A+A^T)x \end{gathered}$$
因此，对拉格朗日函数的求导便很容易理解了：
$$\begin{gathered} \frac{\partial L(\omega )}{\partial \omega }=(\Sigma +{\Sigma }^T)\omega -\lambda (I+I^T)\omega \\ 其中I为单位矩阵 \end{gathered}$$
还记得$\Sigma$是什么吗？由上面定义可知，$\Sigma =\frac{1}{n}{\sum }_{i=1}^n{x}_i{x}_i^T$，很显然，$\Sigma$的转置${\Sigma }^T$=$\Sigma$，因此上面可化简为：
$$\begin{gathered} \frac{\partial L(\omega )}{\partial \omega }=2\Sigma \omega -2\lambda \omega \\ 令其等于0，便可得\Sigma \omega =\lambda \omega \end{gathered}$$

⑦由此，最终可以得到最大方差：
$$D(x)={\omega }^T\Sigma \omega =\lambda {\omega }^T\omega =\lambda$$
至此，公式推导已经完成，现在我们不难看出，x 投影后的方差就是协方差矩阵的特征值，理解了这一点一切就很清晰了。因此，我们要找到最大的方差，也就是相当于要求协方差矩阵的最大特征值，而最佳投影方向就是最大特征值所对应的特征向量。

PCA求解过程总结

​ (1) 对原始样本进行中心化处理，即零均值化

​ (2) 求出样本的协方差矩阵 $\Sigma =\frac{1}{n}{\sum }_{i=1}^n{x}_i{x}_i^T$

​ (3) 求解协方差矩阵的特征值和特征向量

​ (4) 将特征值由大到小排列，取出前 k 个特征值对应的特征向量

​ (5) 将 n 维样本映射到 k 维，实现降维处理。
x i ′ = [ ω 1 T x i ω 2 T x i ⋮ ω k T x i ] 新的 x i ′ 的第 k 维就是 x i 在第 k 个主成分 ω k 方向上的投影 . x_{i}^{'}=\begin{bmatrix}\omega_{1}^{T}x_{i}\\\omega_{2}^{T}x_{i}\\\vdots \\\omega_{k}^{T}x_{i} \end{bmatrix}\\ 新的x_{i}^{'}的第k维就是x_{i}在第k个主成分\omega_{k}方向上的投影. xi′​= ​ω1T​xi​ω2T​xi​⋮ωkT​xi​​ ​新的xi′​的第k维就是xi​在第k个主成分ωk​方向上的投影.

PCA之最近重构性（最小平方误差）

如何理解最近重构性或最小平方误差呢？我们先回顾一下前面讲的最大化方差方法：对于二维空间中的样本点，最大化方差的思想是找到一条直线，使得样本点投影到该直线上的方差最大。因此，也很容易想到，我们可以找到一条直线来更好的拟合这些样本点。从这个角度来理解，求解PCA的问题就可以转化为一个回归问题了。

上面说的是二维空间，可以用直线来拟合，那对于高维空间呢？当然也是可以的。超平面是直线在高维空间的推广，因此，最大化方差就是寻找一个超平面使得样本点在超平面上的投影方差最大，而最小平方误差就是寻找一个超平面使得样本点到这个超平面的距离平方和最小，也就是最近重构性。

下面给出最小化平方误差的优化目标，具体推导就不展开啦~（一般熟悉最大化方差的推导面试就够用了，最小化平方误差的推导作为了解，如果有需要可以参考《百面机器学习》这本书）

最小化平方误差优化目标

①假设超平面D由k个标准正交基$W=\{{\omega }_1,{\omega }_2,...,{\omega }_k\}$构成，$x_d$是样本点$x_d$（中心化后）在超平面D上的投影向量，则每个样本点到 k 维超平面D的距离为：
$$\begin{gathered} dist(x_i,D)=||x_d-x_d|{|}_2 \\ 其中，投影向量x_d可以通过k维正交基线性表示为x_d=\sum _{i=1}^k({\omega }_i^T{x}_d){\omega }_i，而{\omega }_i^T{x}_d是x_d在{\omega }_i方向上的投影长度 \end{gathered}$$
②则PCA的优化目标为：
$$\begin{gathered} \{\begin{array}{l}\underset{{\omega }_1,...,{\omega }_k}{argmin}{\sum }_{d=1}^n||x_d-x_d|{|}_2^2,\\ s.t.\underset{\forall i,j}{{\omega }_i^T{\omega }_j}={\delta }_{i,j}=\{\begin{array}{l}1,i=j;\\ 0,i\ne j.\end{array}\end{array} \\ 通过进一步化简，可得优化目标为：\{\begin{array}{l}\underset{W}{argmax}tr(W^{T}X{X}^{T}W),\\ s.t.W^{T}W=I.\end{array} \end{gathered}$$

因此，可以发现，最小化方差方法求解问题的形式，和最大化方差方法是一致的，因此也同样可以通过求解协方差的特征值所对应的特征向量，从而得到降维后的主成分。

重要的事情不妨多说一遍，因此这里再把求解过程写一遍：

PCA求解过程总结

​ (1) 对原始样本进行中心化处理，即零均值化

​ (2) 求出样本的协方差矩阵 $\Sigma =\frac{1}{n}{\sum }_{i=1}^n{x}_i{x}_i^T$

​ (3) 求解协方差矩阵的特征值和特征向量

​ (4) 将特征值由大到小排列，取出前 k 个特征值对应的特征向量

​ (5) 将 n 维样本映射到 k 维，实现降维处理。
x i ′ = [ ω 1 T x i ω 2 T x i ⋮ ω k T x i ] 新的 x i ′ 的第 k 维就是 x i 在第 k 个主成分 ω k 方向上的投影 . x_{i}^{'}=\begin{bmatrix}\omega_{1}^{T}x_{i}\\\omega_{2}^{T}x_{i}\\\vdots \\\omega_{k}^{T}x_{i} \end{bmatrix}\\新的x_{i}^{'}的第k维就是x_{i}在第k个主成分\omega_{k}方向上的投影. xi′​= ​ω1T​xi​ω2T​xi​⋮ωkT​xi​​ ​新的xi′​的第k维就是xi​在第k个主成分ωk​方向上的投影.

PCA的优缺点

优点： ①它是无监督学习算法，完全无参数限制。

​ ②降维，减小计算开销

缺点： ①特征值分解有一些局限性，比如变换的矩阵必须是方阵

​ ②如果用户对观测对象有一定的先验知识，掌握了数据的一些特征，却无法通过参数化等方法对处理过 程进行干预，可能会得不到预期的效果，效率也不高

应用场景

PCA是一种线性的、无监督的、全局的降维算法。

PCA的应用也很广泛，这里列举其中几项：

​ ①数据降维

​ ②去噪

​ ③高位数据集的可视化

​ ④数据压缩

​ ⑤图像分析

补充：

在本科毕设中，以数字的所有像素坐标作为输入，使用PCA，可以将得到的两个特征向量作为数字的偏转角度，因为这两个特征向量就相当于数字的两个坐标轴。

参考资料

周志华–《机器学习》

葫芦娃–《百面机器学习》

机器学习–主成分分析(PCA)算法的原理及优缺点