CART分类回归_对离散型和连续型特征列的选择
CART分类回归树
分类与回归树是二叉树,可以用于分类,也可以用于回归问题。
区别:分类树输出的是样本的类别, 而回归树输出的是一个实数。
对离散型和连续型特征列的选择
一、CART分类树(待预测结果为离散数据):
选择具有最小Gain_GINI的属性及其属性值,作为最优分裂属性以及最优分裂属性值。Gain_GINI值越小,说明二分之后的子样本的“纯净度”越高,即说明选择该属性(值)作为分裂属性(值)的效果越好。
实现过程:
- 对于样本集S,计算GINI如下:

其中,在样本集S中,pk表示分类结果中第k个类别出现的频率; - 对于含有N个样本的样本集S,根据属性A的第i个属性值,将数据集S划分成两部分,则划分成两部分之后,Gain_GINI计算如下:

- 对于属性A,分别计算任意属性值将数据集划分成两部分之后的Gain_GINI,选取其中的最小值,作为属性A得到的最优二分方案;
- 对于样本集S,计算所有属性的最优二分方案,选取其中的最小值,作为样本集S的最优二分方案:所得到的属性A及其第i属性值,即为样本集S的最优分裂属性以及最优分裂属性值。
举个简单的例子,如下图:

在上述图中,属性有3个,分别是有房情况,婚姻状况和年收入,其中有房情况和婚姻状况是离散的取值,而年收入是连续的取值。拖欠贷款者属于分类的结果。
假设现在来看有房情况这个属性,那么按照它划分后的基尼增益计算如下:
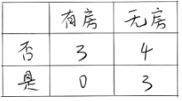
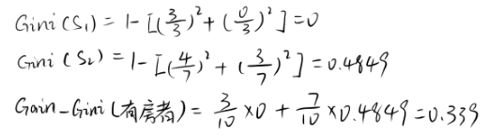
而对于婚姻状况属性来说,它的取值有3种,按照每种属性值分裂后基尼增益计算如下:
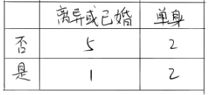

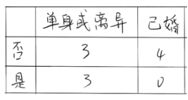
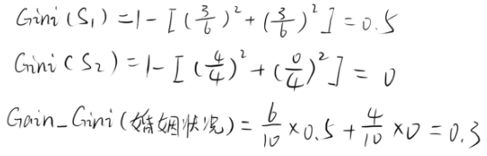
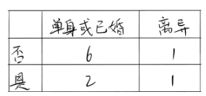
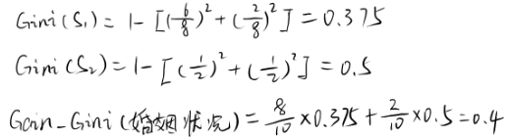
比较上述三种取值得到的基尼增益可知,以“已婚”这个取值来分裂婚姻状况属性是最好的。
二、CART回归树(待预测结果为连续型数据)
区别于分类树选取Gain_GINI为评价分裂属性的指标,回归树选取Gain_σ(方差)为评价分裂属性的指标。选择具有最小Gain_σ的属性及其属性值,作为最优分裂属性以及最优分裂属性值。Gain_σ值越小,说明二分之后的子样本的“差异性”越小,说明选择该属性(值)作为分裂属性(值)的效果越好。
实现过程:
- 对于含有连续预测结果的样本集S,总方差计算如下:

其中,μ表示样本集S中预测结果的均值,yk表示第k个样本预测结果; - 对于含有N个样本的样本集S,根据属性A的第i个属性值,将数据集S划分成两部分,则划分成两部分之后,Gain_σ计算如下:
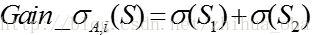
- 对于属性A,分别计算任意属性值将数据集划分成两部分之后的Gain_σ,选取其中的最小值,作为属性A得到的最优二分方案;
- 对于样本集S,计算所有属性的最优二分方案,选取其中的最小值,作为样本集S的最优二分方案:所得到的属性A及其第i属性值,即为样本集S的最优分裂属性以及最优分裂属性值。
继续拿上面那个数据集来讲解上述的步骤:
1、 根据第1个属性值划分为<=125和>125两部分:
<=125的有:125, 100, 70, 120, 95, 60, 85, 75, 90 均值为91.111
>125的有:220 均值为220
σ(S1) = 61.554
σ(S2) = 0
Gain_σ(S) = σ(S1) + σ(S2) = 61.554
2、 根据第2个属性值划分为<=100和>100两部分:
<=100的有:100, 70, 95, 60, 85, 75, 90 均值为82.143
而>100的有:125,120,220 均值为155
σ(S1) = 35.254
σ(S2) = 79.687
Gain_σ(S) = σ(S1) + σ(S2) = 114.941
3、 根据第3个属性值划分为<=70和>70两部分:
Gain_σ(S) = σ(S1) + σ(S2) =129.085
4、 根据第4个属性值划分为<=120和>120两部分:
Gain_σ(S) = σ(S1) + σ(S2) =117.144
5、 根据第5个属性值划分为<=95和>95两部分:
Gain_σ(S) = σ(S1) + σ(S2) =122.347
6、 根据第6个属性值划分为<=60和>60两部分:
Gain_σ(S) = σ(S1) + σ(S2) =128.798
7、 根据第7个属性值划分为<=220和>220两部分:
Gain_σ(S) = σ(S1) + σ(S2) =136.894
8、 根据第8个属性值划分为<=85和>85两部分:
Gain_σ(S) = σ(S1) + σ(S2) =126.656
9、 根据第9个属性值划分为<=75和>75两部分:
Gain_σ(S) = σ(S1) + σ(S2) =125.568
10、 根据第10个属性值划分为<=90和>90两部分:
Gain_σ(S) = σ(S1) + σ(S2) =125.511
比较每一种划分得到的Gain_σ(S)可知,用“125”来划分“年收入”这个属性是最合适的。
这样一来,连续型的这个属性也可以被划分为两部分:

计算它的基尼增益:

到此每个属性的最优二分方案均已计算出,比较每个属性的基尼增益可得出:此数据集的最优分裂属性为“婚姻状况”(因为这个属性的基尼增益值最小,为0.3),以及最优分裂属性值为“已婚”。