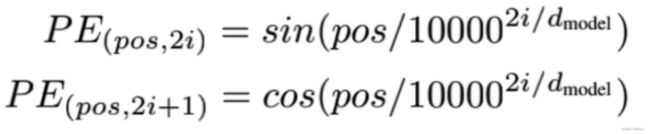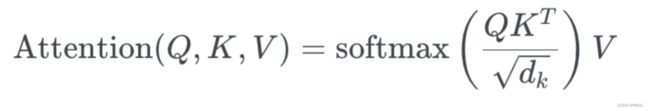保姆级讲解Transformer

原创不易，转载请注明出处

一、模型背景

• paper：Attention Is All You Need

  • https://papers.nips.cc/paper/7181-attention-is-all-you-need.pdf
    

• 论文中给出Transformer的定义是：

  Transformer is the first transduction model relying entirely on self-attention to compute representations of its input and output without using sequence aligned RNNs or convolution。

• 发展动机：

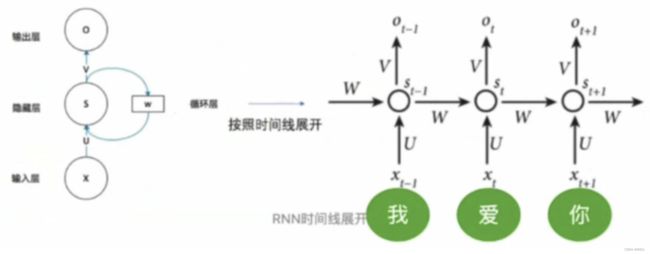
  • 目前在序列建模和转换问题中，如语言建模和机器翻译，所采用的主流框架为Encoder-Decoder框架。传统的Encoder-Decoder一般采用RNN作为主要方法，基于RNN所发展出来的LSTM和GRU也被曾认为是解决该问题最先进的方法。而RNN模型的计算被限制为顺序，这种机制阻碍了样本训练的并行化，又会导致在计算过程中信息丢失从而引发长期依赖问题。RNN及其衍生网络的缺点就是慢，问题在于前后隐藏状态的依赖性，无法实现并行。

• transformer为何优于RNN及RNN的一系列变体？

  • Transformer中抛弃了传统的CNN和RNN，整个网络结构完全是由Attention机制组成。 作者采用Attention机制的原因是考虑到RNN（或者LSTM，GRU等）的计算限制为是顺序的，也就是说RNN相关算法只能从左向右依次计算或者从右向左依次计算，这种机制带来了两个问题：
  • 时间片$t$的计算依赖$t-1$时刻的计算结果，这样限制了模型的并行能力。
  • 顺序计算的过程中信息会丢失，尽管LSTM等门机制的结构一定程度上缓解了长期依赖的问题，但是对于特别长期的依赖现象，LSTM依旧无能为力。

如上图所示，不管中间用的是RNN还是GRU，它们都无法避免一种情况：它们是前后相互依赖的(图中箭头)，对于后面的输出，它依赖的是前面的状态和当前的输入。

这就意味着，我们想要得到这个输出，那就必须得到前面的状态。所以必须要走完上一步，才能走下一步。所以说它的计算被限制为顺序，阻碍了样本的并行化训练。

• transformer特点
  • 基于Attention机制，将序列中任意两个位置之间的距离缩小为一个常量。
  • Transformer利用self-attention机制实现快速并行，改进了RNN/LSTM最被人诟病的训练慢的缺点，同时也符合现有GPU框架的矩阵化训练。
  • Transformer可以增加到非常深的深度跳跃连接，充分发掘DNN模型的特性，提升模型准确率。

二、引入讲解的任务场景

方便讲解，和原论文一致是机器翻译场景。

三、模型整体结构

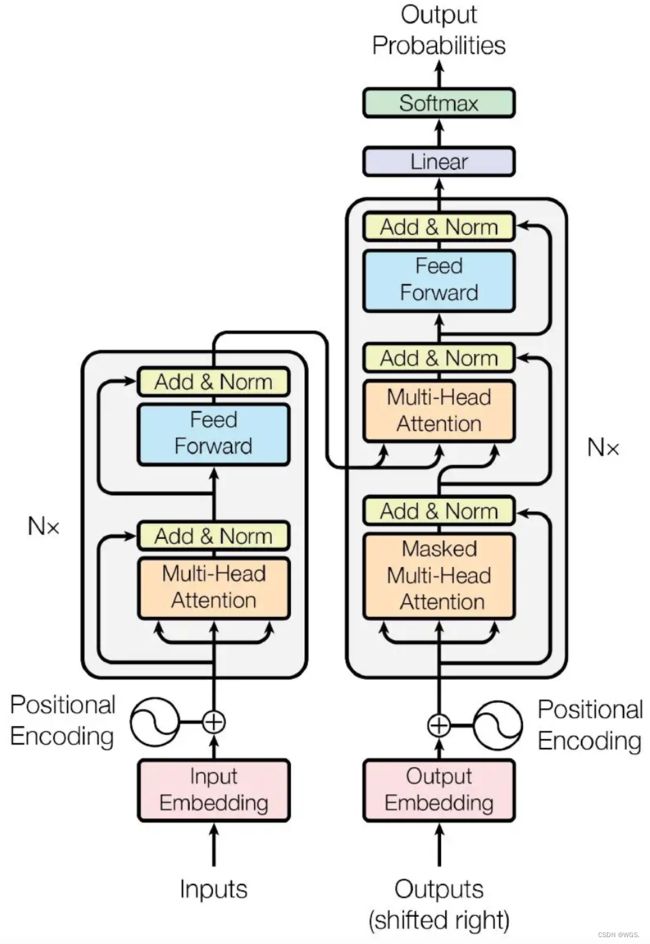
3.1 模型结构图

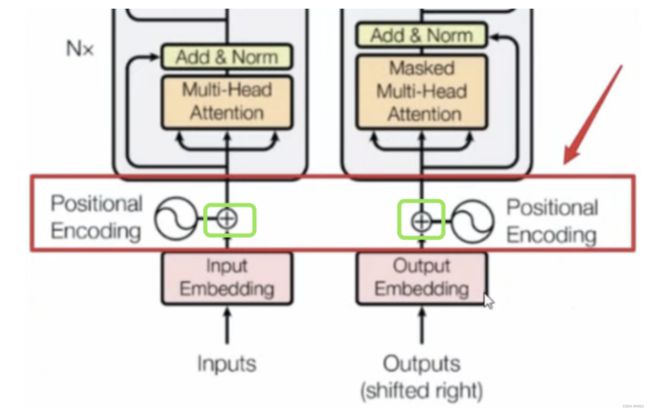
• 这是论文中的原图，可以看到左右两边都有乘N，左半部分就是encoders，右半部分就是decoders
• 自底向上看各部分为：
  • 1.首先是encoder部分的输入和decoder部分的输入，经过Embedding；
  • 2.其次是Positional Encoding（位置编码）；
  • 3.其次是Multi-Head Attention（多头注意力机制）；
  • 4.其次是Add&Norm（跳跃连接&LayerNorm）；
  • 5.其次是Feed Forward（前馈神经网络）；
  • 6.其次是输出层（Linear、Softmax）。

3.2 宏观举例理解

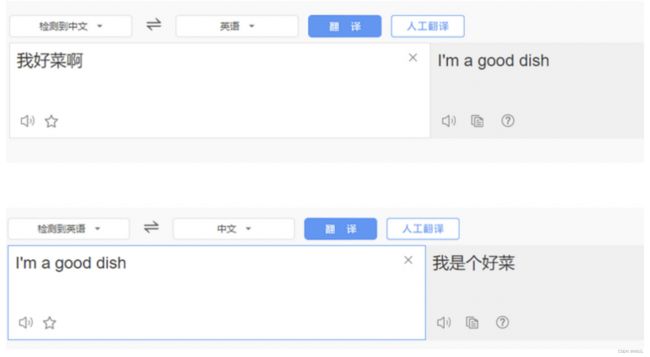
比如输入一段法语，经过transformer，翻译成对应的英语。

3.3 微观拆解理解

3.4 机器翻译工作流程举例

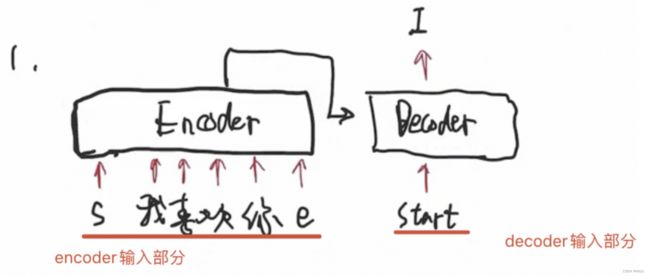
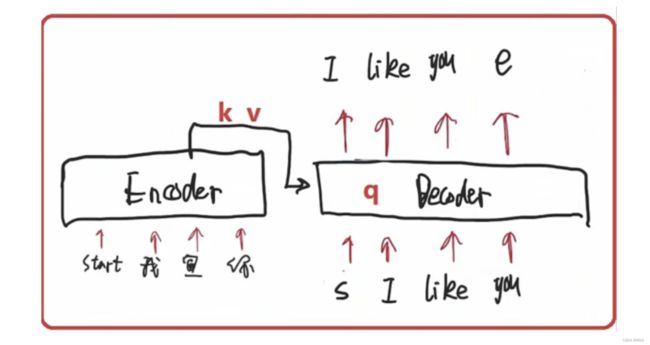
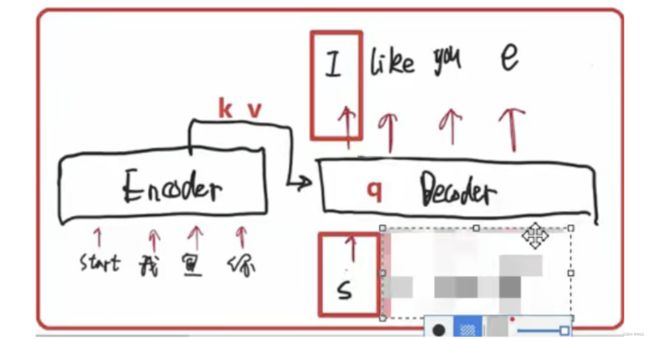
• 第一步：输入要翻译的英文，即encoder端的输入：“Why do we work？”；
• 第二步：经过encoder部分的运算后，将隐层输出到decoder端；
• 第三步：decoder部分输入，这里需要注意的是因为预测的时候是一个单词一个单词预测的，所以先输入的是起始符"start"
• 第四步：经过decoder部分的运算输出"为"；
• 第五步：有了"为"之后，可以用"start 为"预测"什"；
• 然后重复执行，直到遇到结束符表示预测结束。

如果是第一次接触机器翻译的同学可能会觉得云里雾里，那么博主再以中英翻译为例举个例子帮助小伙伴们理解：

• 每句话都包含起始符s、结束符e
• 下面看下流程解释：

• 这句话输进来都会在encoder部分进行并行化运算，将encoder传过来的语义信息和decoder初始化的起始符，预测下一个要产生的单词是谁。比如输出"I"。

• 第2步的时候，decoder的输入就变成了两个，即它会拿上一步的输出，当做下一步的输入。用’start’和’I’预测出’like’。

• 上一步的输出’like’变成了下一步的输入，也是先将I和like屏蔽掉，用start预测出I，用’start I’预测出like，在用’start I like’预测出you。

四、输入部分&Embedding

在一个机器翻译场景中的数据预处理部分一般包括以下几个步骤：

• 1.将字符串转为数字编码；
• 2.按句子长度进行过滤；
• 3.添加起始符与结束符；
• 4.mini-batch、padding填充。

这里没什么好讲的，直接上示例代码

import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt
import math

'''句子的输入部分：编码端的输入、解码端的输入、解码端的真实标签'''
# P指padding、S指起始符、E指结束符
sentences = [['我 喜 欢 你 P', 'S i like you', 'i like you E'],
             ['我 喜 欢 你 P', 'S i like you', 'i like you E'],
             ['我 喜 欢 你 P', 'S i like you', 'i like you E']]

'''构建词表，编码端和解码端可以共用一个词表，这里方便演示分开构建'''
# encoder端词表及词表大小
src_vocab = {'P': 0, '我': 1, '喜': 2, '欢': 3, '你': 4}
src_vocab_size = len(src_vocab)

# decoder端词表及词表大小
tgt_vocab = {'P': 0, 'i': 1, 'like': 2, 'you': 3, 'S': 4, 'E': 5}
tgt_vocab_size = len(tgt_vocab)

src_len = 5  # length of source
tgt_len = 4  # length of target

'''将单词与词表映射，这里可以理解为label编码'''
enc_inputs, dec_inputs, target_batch = make_batch(sentences)

print(enc_inputs)
print(dec_inputs)
print(target_batch)

tensor([[1, 2, 3, 4, 0],
        [1, 2, 3, 4, 0],
        [1, 2, 3, 4, 0]])
tensor([[4, 1, 2, 3],
        [4, 1, 2, 3],
        [4, 1, 2, 3]])
tensor([[1, 2, 3, 5],
        [1, 2, 3, 5],
        [1, 2, 3, 5]])

'''将单词与词表映射，这里可以理解为label编码，把单词序列转换为数字序列'''
def make_batch(sentences):
    input_batch, output_batch, target_batch = [], [], []
    for sentence in sentences:
        input_batch.append([src_vocab[n] for n in sentence[0].split()])
        output_batch.append([tgt_vocab[n] for n in sentence[1].split()])
        target_batch.append([tgt_vocab[n] for n in sentence[2].split()])

    return torch.LongTensor(input_batch), torch.LongTensor(output_batch), torch.LongTensor(target_batch)

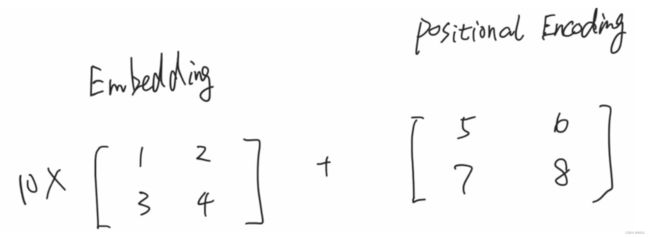
这里简单的来说一下什么是embedding，用一个向量来表征一个单词或是一个句子，这就是embedding，解决了传统onehot离散化带来的稀疏性问题。embedding作为网络的第一层被输入。

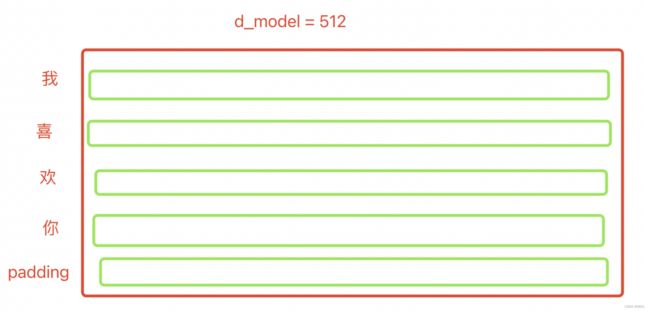
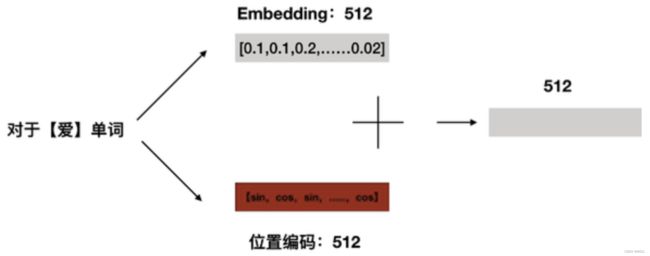
比如上述例子，“我喜欢你”，对这句话做一个512维的embedding，如下图：

# 其中src_vocab_size指词表大小，d_model为emb维度
self.src_emb = nn.Embedding(num_embeddings=src_vocab_size, embedding_dim=d_model)

在forward里，我们需要知道emb后的维度为：[batch_size, src_len, d_model]，上述例子中就是：[3, 5, 512]

enc_outputs = self.src_emb(enc_inputs)

tensor([[[-0.6629,  0.7175, -1.2013,  ...,  1.3913, -0.7109,  0.4084],
         [-0.0628, -0.0403, -0.0125,  ..., -0.7531,  1.2500, -0.6480],
         [-1.0983, -0.2127, -0.1055,  ..., -0.2792, -1.1022, -1.6856],
         [ 0.7872, -0.0841, -0.0297,  ...,  0.1816, -0.4747, -0.6163],
         [ 0.8541, -0.0226,  0.3261,  ..., -0.8943, -1.6848,  1.0269]],

        [[-0.6629,  0.7175, -1.2013,  ...,  1.3913, -0.7109,  0.4084],
         [-0.0628, -0.0403, -0.0125,  ..., -0.7531,  1.2500, -0.6480],
         [-1.0983, -0.2127, -0.1055,  ..., -0.2792, -1.1022, -1.6856],
         [ 0.7872, -0.0841, -0.0297,  ...,  0.1816, -0.4747, -0.6163],
         [ 0.8541, -0.0226,  0.3261,  ..., -0.8943, -1.6848,  1.0269]],

        [[-0.6629,  0.7175, -1.2013,  ...,  1.3913, -0.7109,  0.4084],
         [-0.0628, -0.0403, -0.0125,  ..., -0.7531,  1.2500, -0.6480],
         [-1.0983, -0.2127, -0.1055,  ..., -0.2792, -1.1022, -1.6856],
         [ 0.7872, -0.0841, -0.0297,  ...,  0.1816, -0.4747, -0.6163],
         [ 0.8541, -0.0226,  0.3261,  ..., -0.8943, -1.6848,  1.0269]]],
       grad_fn=) torch.Size([3, 5, 512])

五、位置编码（Positional Encoding）

5.1 为什么要引入位置编码？

从图中我们发现，embedding后要加上位置编码，那么为什么要假如位置编码呢？

这就要引入并行化计算带来的问题，也就是传统RNN循环网络的特点：

在本文的最开始也提到过，它是有前后依赖的语义关系的，在生成”爱“之前必须生成”我“，生成”爱“之后才能生成”你“。

具体的，由于句子中单词的序列关系，所以后一个timestep的输入必须等于前一个timestep的输出，它不具备并行处理的能力；

并且RNN中的每个timestep共享一套参数$u，w，v$，所以会出现梯度消失或梯度爆炸的问题；

相对于attention，它具有并行处理的能力，但并不具有位置信息显示的能力。

ps：这里插一个面试小问题，RNN的梯度消失有什么不同？
连乘效应导致梯度消失放在RNN这里不是太准确，RNN的梯度是一个总的梯度和，它的梯度消失不单单是梯度和变为0，而是说总体的梯度被近距离梯度主导，被远距离梯度忽略不计，这才是RNN梯度消失的真正含义。

• transformer因为有注意力所以是并行化的计算，所以语义位置信息就没有了，没有办法去理解”我
  “在”爱“前面。
• 比如输入是”你礼貌吗“，如果将位置信息打乱，变成”礼貌你吗“的时候，因为模型没有位置信息所
  以也就没办法识别语义，但是从人的⻆度理解这是完全不同的两句话。

所以就有了位置编码，解决方案:引入绝对位置信息和相对位置信息。

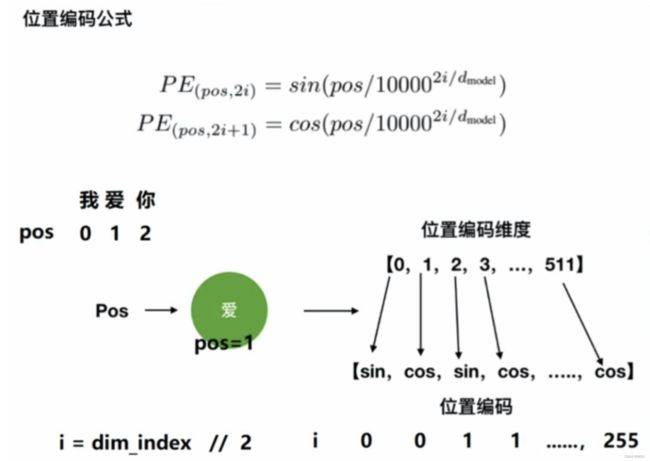
上图就是偶数位置使用 sin 函数，奇数位置使用 cos 函数。

根据位置编码公式，可以将emb向量的每个值来区分开来，也可以将每句话来区分开来，比如告诉模型 ”我“ 是在 “喜” 之前的。

将位置编码后的向量和embedding进行对位相加，作为整个transformer的输入

• pos指的就是这句话的每个位置，比如起始符s的pos就是1，“我”的pos就是2，也可以认为是这个向量的顺序。
• 2i代表偶数位置，2i+1代表奇数位置。
  • i=emb向量的下标对2求模，如图所示假如有512维的emb向量，当emb向量索引为0的位置时，它的i就是$0//2=0$，同理1的位置是$1//2=0$，以此类推…
• d_model指的是emb向量的维度，也是个定值。

所以根据公式，就能计算出emb向量的位置编码张量。

观察可以发现:
位置编码跟句子⻓度seq_len有关，它由pos决定，句子有多⻓就决定了pos从多少到多少;其次还和emb向量的维度有关。
一旦这两个确定了，那么位置编码就根据公式唯一的确定了。它跟emb向量内的值没有关系。只和seq_len和d_model有关系。

总结来说，当d_model和seq_length确定，位置编码即可确定。

引入位置编码的同时，也引入了绝对位置信息与相对位置信息。

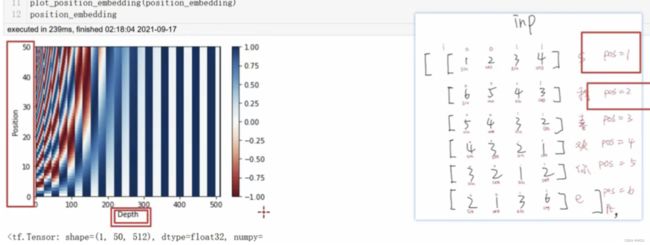
5.2 绝对位置如何体现？

如下图：

def plot_position_embedding(position_embedding):
# 绘制位置编码
    plt.pcolormesh(position_embedding[0],cmap='RdBu') # 【50*512】
    plt.xlabel('Depth')
    plt.xlim((0,512))
    plt.ylabel('Position')
    plt.colorbar()
    plt.show()

position_embedding = positional_encoding(50,512)
plot_position_embedding(position_embedding)
position_embedding

• d_model=512，seq_length=50；
• 纵坐标就是pos，横坐标就是emb的维度；
• 右侧颜色的深浅就是代表数值的大小；

可以这样认为，从下往上看:

• 第一个横条是“起始符”这个向量的位置编码；
• 第二个是“我”这个向量的位置编码；
• 第三个是“喜”这个向量的位置编码…；
• 我们可以看到每个向量是独一无二的，那么这个就是一个绝对位置信息；因为它是唯一标识的，每个词的位置编码向量都是独一无二的。仔细观 察这些条纹还有周期性变化的规律。

5.3 相对位置如何体现？

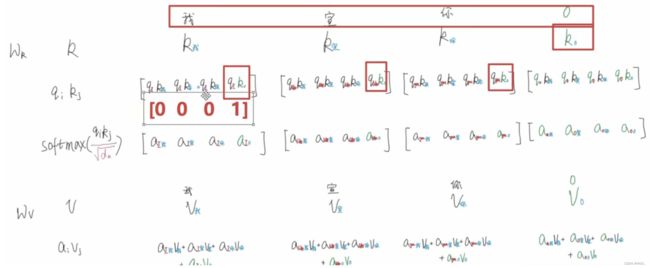
根据三角函数公式：

$$\begin{gathered} sin(\alpha +\beta )=sin(\alpha )cos(\beta )+cos(\alpha )sin(\beta ) \\ cos(\alpha +\beta )=cos(\alpha )cos(\beta )+sin(\alpha )sin(\beta ) \end{gathered}$$

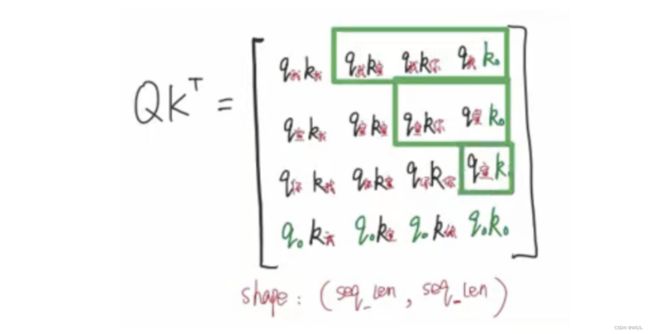
上面的公式说明：对于词汇之间的位置偏移$k$，$PE(pos+k)$可以表示成$PE(pos)$和$PE(k)$的组合形式，这就是表达相对位置的能力。

$$\{\begin{array}{l}PE(pos+k,2i)=PE(pos,2i)\ast PE(k,2i+1)+PE(pos,2i+1)\ast PE(k,2i)\\ PE(pos+k,2i+1)=PE(pos,2i+1)\ast PE(k,2i+1)-PE(pos,2i)\ast PE(k,2i)\end{array}$$

说的更直白一点，上图中，红框的位置编码数值可以由绿框、紫框、粉框、蓝框推得而来，也就是表达了相对位置的效果。

ps：这里有一个小trick，就是在位置编码之前加一个缩放：
当emb和位置编码相加了之后，我们希望emb占多数，比如将emb放大10倍，那么在相加后的张 量里，emb就会占大部分。
因为主要的语义信息是蕴含在emb当中的，我们希望位置编码带来的影响不要超过emb。所以对 emb进行了缩放再和位置编码相加。

5.4 位置编码代码示例

由位置编码公式可知，它们的一个共同的部分：$pos/10000^{2i/d_{model}}$

我们用log将次方拿下来方便计算：

$$\begin{gathered} pos/10000^{2i/d_{model}} \\ =pos\ast 10000^{-2i/d_{model}} \\ =pos\ast e^{-2i/d_{model}\ast ln(10000)} \end{gathered}$$

'''   3. PositionalEncoding 代码实现   '''
class PositionalEncoding(nn.Module):
    '''
        位置编码的实现其实很简单，直接对照着公式去敲代码就可以，下面这个代码只是其中一种实现方式；
        从理解来讲，需要注意的就是偶数和奇数在公式上有一个共同部分，我们使用log函数把次方拿下来，方便计算；
        pos代表的是单词在句子中的索引，这点需要注意；比如max_len是128个，那么索引就是从0，1，2，...,127
        假设我的d_model是512，2i那个符号中i从0取到了255，那么2i对应取值就是0,2,4...510
    '''
    def __init__(self, d_model, dropout=0.1, max_len=5000):
        super(PositionalEncoding, self).__init__()

        self.dropout = nn.Dropout(p=dropout)

        pe = torch.zeros(max_len, d_model)
        # 生成0~max_len-1的索引位置张量，[max_len] -> [max_len, 1]
        position = torch.arange(0, max_len, dtype=torch.float).unsqueeze(1)
        div_term = torch.exp(torch.arange(0, d_model, 2).float() * (-math.log(10000.0) / d_model))
        # 这里需要注意的是pe[:, 0::2]这个用法，就是从0开始到最后面，步长为2，其实代表的就是偶数位置
        pe[:, 0::2] = torch.sin(position * div_term)
        # 这里需要注意的是pe[:, 1::2]这个用法，就是从1开始到最后面，步长为2，其实代表的就是奇数位置
        pe[:, 1::2] = torch.cos(position * div_term)
        # 上面代码获取之后得到的pe:[max_len * d_model]
        # 下面这个代码之后，我们得到的pe形状是：[max_len * 1 * d_model]
        pe = pe.unsqueeze(0).transpose(0, 1)

        # 定一个缓冲区，其实简单理解为这个参数不更新就可以
        self.register_buffer('pe', pe)

    def forward(self, x):
        """
        x: [seq_len, batch_size, d_model]
        """
        x = x + self.pe[:x.size(0), :]
        return self.dropout(x)

受篇幅和排版限制，下面各部分代码不再本文贴出，文章的末尾会放出Git连接，需要的小伙伴可自行下载。

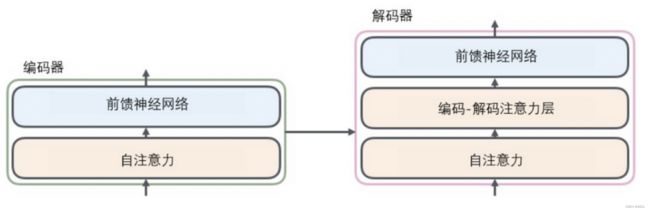
六、Encoder部分

Encoder部分输入是单词的Embedding，再加上位置编码，然后进入一个统一的结构，这个结构可以循环很多次（N次），也就是说有很多层（N层）。每一层又可以分成Attention层和全连接层，再额外加了一些处理，比如Skip Connection，做跳跃连接，然后还加了Normalization层。其实它本身的模型还是很简单的。

6.1 多头注意力机制（Multi-Head Attention）

关于Attention部分（Attention、Self-Attention、Multi-Head Attention）这里不再详细讲解，直接已经讲过了，没看过的同学可以看下：https://mp.weixin.qq.com/s?__biz=Mzk0MzIzODM5MA==&mid=2247484067&idx=1&sn=cae143a546985413507d3bc750f5f7d6&chksm=c337bf3af440362c67f9ac26e82a5a537c1ea09c9041dfc7cfeae35fe93a9b797700bafe7db4#rd

6.1.1 理解self-attention

• 没有self-attention的情况下，每个词只表示自身的含义，不包含语义信息。
• 含有self-attention，对词向量进行重构，使得词向量不单只包含自己，而是综合考虑全局，融入上下文。

这里只是对于Attention的举例简述，如果没看懂的同学可以去上面的链接详细的了解Attention

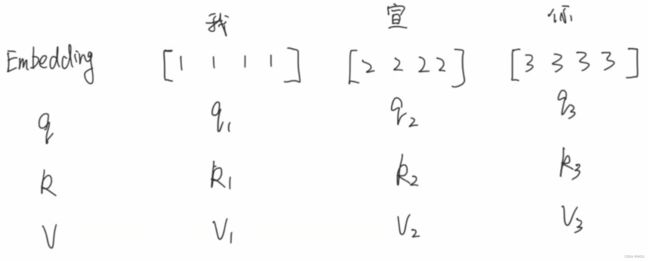
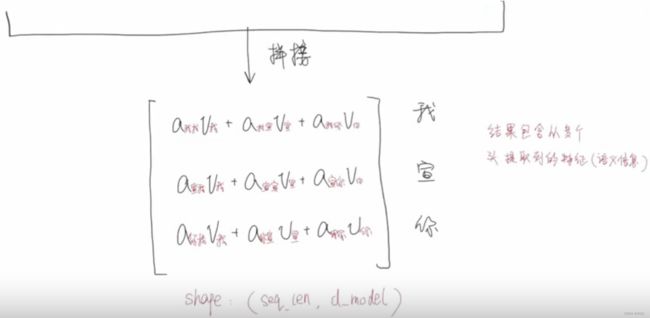
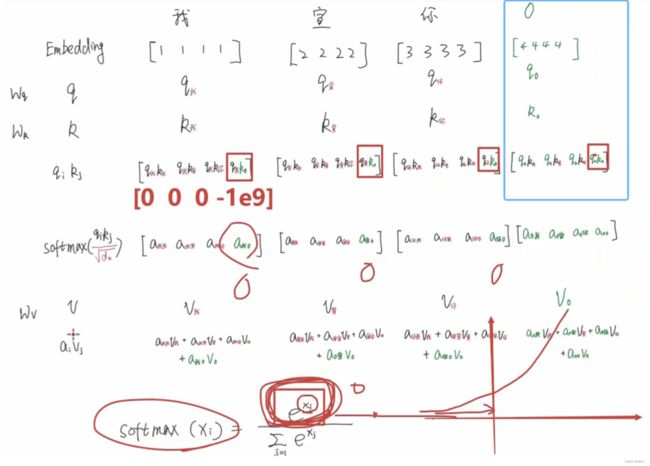
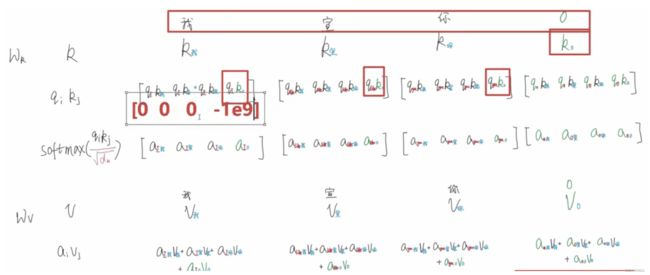
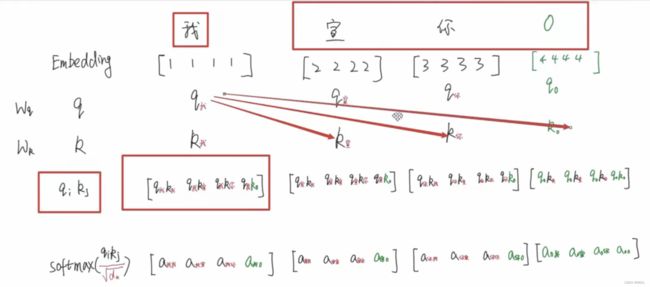
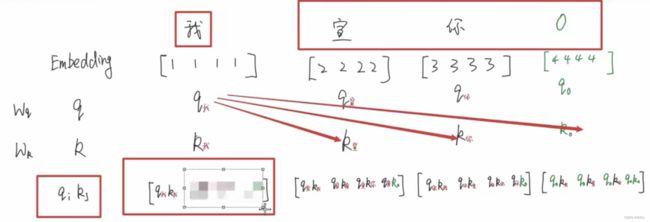
我们这里以三个向量举例理解Attention：

• 假设我们现在有3个词向量分别为:“我”、“宣”、“你”;
• 对于每一个emb向量，都会通过$w_q、w_k、w_v$来线性变换生成各自的q、k、v；
  • 这里的线性变换其实就是矩阵相乘，比如$X_1$的维度是（1, 4），初始化一个$W_Q$矩阵维度为（4, 3），那么$Q$的维度就是（1, 3）；
  • 需要注意的是，本文以$Q、q$来进行区分，分别代表矩阵和向量，方便理解这里用的向量举例；
• w矩阵是需要学习的;

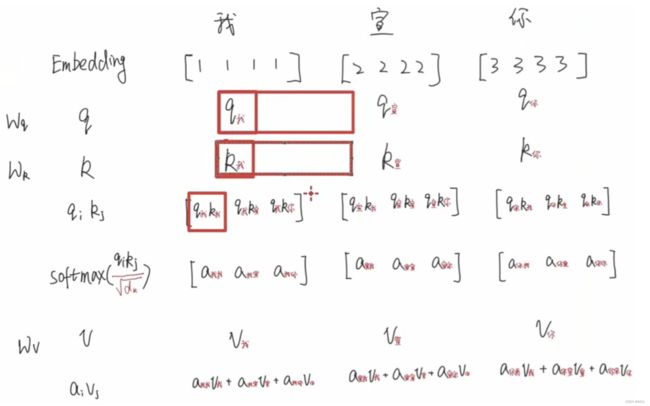
• 首先将q和k进行点乘操作，来计算其相关性系数，可以理解为计算它们的关联程度有多大;
• 在上图例子中，对于每一个q，都要和每个k做相关性的匹配。我们要看某个字在这句话的语义信息，所以要综合其在整句话中的作用，所以就必须要和其它字做交互;
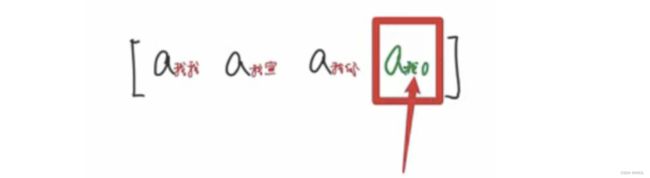
• 需要注意的是，"我"和“宣”之间的关系，和“宣”和“我”之间的关系，是不相等的。
  • 就好比我看到一个女生对着我笑，那这个时候我也许会觉得我很酷，帅气侧漏，是这个女生喜欢我，所以才对着我笑，所以 $q_{我}{k}_{宣}$ 的分数应该挺高的；
  • 但实际上这个女生看到我笑可能是笑我胖，所以她给我的分数 $q_{宣}{k}_{我}$ 可能是一个比较低的分数;
• 然后将得分送到注意力层进行归一化，映射到0-1之间，生成注意力权重，
  • 比如“我”和“我”可能会觉得相关性比较大，所以$a_{我我}$可能会比较大，
  • 假设 $a_{我我},a_{我宣},a_{我你}=[0.8,0.1,0.1]$ ;
• softmax后的权重再和v做加权，可以理解为“我”这个向量，需要从“我”里抽取多少语义信息出来、从“宣”中抽取多少语义信息出来、从“你”中抽取多少语义信息出来。抽取后全部加起来形成新的向量去表示“我”。那么这样一来，“我”的向量就结合了上下文的语义信息。就不再是原来的emb向量仅仅代表“我”这个字的含义。

6.1.2 scaled dot-product attention 缩放点积注意力

公式如下：

再啰嗦一句，上面的例子都是向量，用了小写。这里是矩阵的形式，是张量，所以是大写。

缩放是指除以${\sqrt{d}}_k$，$d_k$指的是embedding的维度。

6.1.3 前向传播角度理解为什么要除以${\sqrt{d}}_k$

首先我们要明白的一点是：softmax是一种非常明显的⻢太效应 强者越强，弱者越弱。

而缩放后，注意力值就分散些，这样就可以获得更好的泛化能力;

举个例子：

print(tf.math.softmax([[1.0, 2.0, 3.0]]))
print(tf.math.softmax([[10.0, 20.0, 30.0]]))
print(tf.math.softmax([[100.0, 200.0, 300.0]]))

tf.Tensor([[0.09003057 0.24472848 0.66524094]], shape=(1, 3), dtype=float32)
tf.Tensor([[2.061060e-09 4.539787e-05 9.999546e-01]], shape=(1, 3), dtype=float32)
tf.Tensor([[0.0e+00 3.8e-44 1.0e+00]], shape=(1, 3), dtype=float32)

• 如果向量的维度比较大，那么qk点积之后的结果也会比较大，$q_{我}{q}_{我}、q_{我}{q}_{宣}...$ 这些数的数量积都会比较大，
• 如果没有经过缩放的话，softmax很有可能就剩下[0, 0, 1]的结果了，那它就会表示“我”和“我”、“我”和“宣”一点关系都没有，“我”和“你”却有100%的关系。很明显这是不合理的，与我们引入上下文语义信息相悖。

这里论中也给出了为什么要这么做：

为什么非要将均值和方差拉到0和1呢?

这是ICS内部协变量偏移问题：

• 机器学习都有一个前提假设那就是数据符合标准正态分布的，
• 那么样本经过emb之后，也是符合正太分布的，
• q、k的线性变换也是符合正太分布的。
• 当到qk的时候，就发生了变化，因为点积的操作分布就不再是标准正态分布了，也会影响后续所有数据的分布。

所以我们现在的问题是：

• 有两个向量：
  $$\begin{gathered} q=[q_1,q_2,...,q_{dk}] \\ k=[k_1,k_2,...,k_{dk}] \\ 随机变量q_i、k_i的取值均服从标准正态分布 \\ 其中dk为emb维度 \end{gathered}$$

• 求：
  $$\begin{gathered} （1）q\odot k=[q_1{k}_1,q_2{k}_2,...,q_{dk}{k}_{dk}] \\ 中随机变量q_i{k}_i所服从的分布的期望与方差 \end{gathered}$$
  $$\begin{gathered} （2）设Z=q\cdot k^T=q_1{k}_1+q_2{k}_2+...+q_{dk}{k}_{dk} \\ 的E(Z)、D(Z) \end{gathered}$$

• 1.获取条件，设置定义

$$\begin{gathered} 对于{\forall }_i\in dk \\ 设随机变量X=q_i，Y=k_i，XY=q_i{k}_i \\ 有： \\ \{\begin{array}{l}E(X)=0\\ E(Y)=0\end{array}\{\begin{array}{l}D(X)=1\\ D(Y)=1\end{array} \end{gathered}$$

• 2.求均值

$$\begin{gathered} 则有： \\ E(XY)=E(X)\cdot E(Y)=0 \\ 含义：随机变量q_i{k}_i服从均值为0的分布 \\ 即：q\odot k=[q_1{k}_1,q_2{k}_2,...,q_{dk}{k}_{dk}] \\ 只要dk足够大，mean(q\odot k)=0 \end{gathered}$$

• 3.求方差

$$\begin{gathered} 由公式D(X)=E(X^2)-E^2(X) \\ 得： \\ \begin{array}{rl}D(XY)=& E(X^2{Y}^2)-[E(XY){]}^2\\ =& E(X^2)E(Y^2)-[E(X)E(Y){]}^2\\ =& [E(X^2)-0][E(Y^2)-0]-[E(X)E(Y){]}^2\\ =& [E(X^2)-E^2(X)][E(Y^2)-E^2[Y]]-[E(X)E(Y){]}^2\\ =& D(X)D(Y)-[E(X)E(Y){]}^2\\ =& 1\ast 1-0\\ =& 1\end{array} \\ 含义：随机变量q_i{k}_i服从方差为1的分布 \\ 即：q\odot k=[q_1{k}_1,q_2{k}_2,...,q_{dk}{k}_{dk}] \\ 只要dk足够大，方差(q\odot k)=1 \end{gathered}$$

• 4.求E(X)和D(Z)

$$\begin{array}{rl}E(Z)=& E(XY)\\ =& E(q_1{k}_1)+E(q_2{k}_2)+...+E(q_{dk}{k}_{dk})\\ =& 0+0+...+0\\ =& 0\\ D(Z)=& D(XY)\\ =& D(q_1{k}_1)+D(q_2{k}_2)+...+D(q_{ak}{k}_{ak})\\ =& 1+1+...+1\\ =& dk\\ & 因为有dk项\end{array}$$

经过推导，所以这里的数值对应的就是均值为0，方差为dk。

我们需要将方差重新变为1

• 5.将$Q{K}^T$转回$E(X)=0、D(X)=1$的标准正太分布中

$$\begin{array}{rl}& 由D(Z)=dk\\ & 设\alpha 为线性变换因子(常数)\\ & D(\alpha Z)=1\\ & 则有D(\alpha Z)={\alpha }^{2}D(Z)={\alpha }^{2}dk=1\\ & 得\alpha =\frac{1}{\sqrt{d}k}\\ & 因此，只需将Z=Q{K}^T，乘上一个\frac{1}{\sqrt{d}k}即可！！！\end{array}$$

以上就是从前向传播角度推导为何要除以$\sqrt{d}k$，当然Markdown里公式打起来比较费劲，排版不太好看，各位小伙伴体谅一下。

6.1.4 反向传播角度理解为什么要除以${\sqrt{d}}_k$

其实很容易理解：不除以的话，注意力得分score是一个很大的值，softmax在反向传播时，容易造成梯度消失。

以上面马太效应的例子来看下

print(tf.math.softmax([[100.0, 200.0, 300.0]]))
# tf.Tensor([[0.0e+00 3.8e-44 1.0e+00]], shape=(1, 3), dtype=float32)

根据softmax公式，求偏导可得：

$$\begin{array}{rl}& a_j=softmax(x_j)=\frac{e^{x_j}}{{\sum }_{i=1}{e}^{x_j}}\\ & \frac{\partial a_j}{\partial x_j}=a_j(1-a_j)\end{array}$$

• 当$x_j$为最大值时，softmax的结果$a_j=1$，$梯度值=1\ast (1-1)=0$
• 当$x_j$为其它值时，softmax的结果$a_j=0$，$梯度值=0\ast (1-0)=0$

所以说，如果不除以的话，由于softmax的马太效应，在求偏导计算梯度的时候，梯度值为0，导致参数无法更新，即梯度消失。

经过缩放之后，$a_j$就不再是0或是1了，梯度值就能够正常的进行参数的更新。

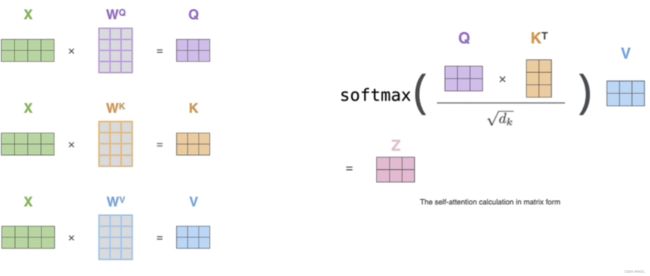
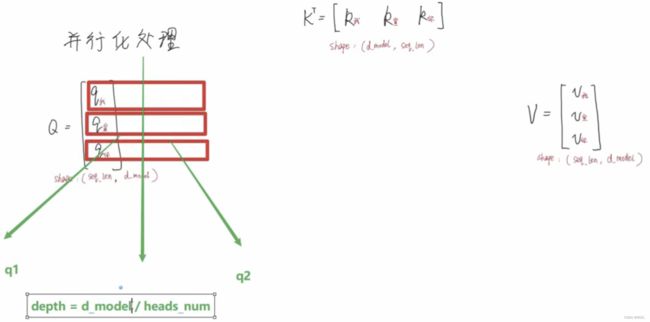
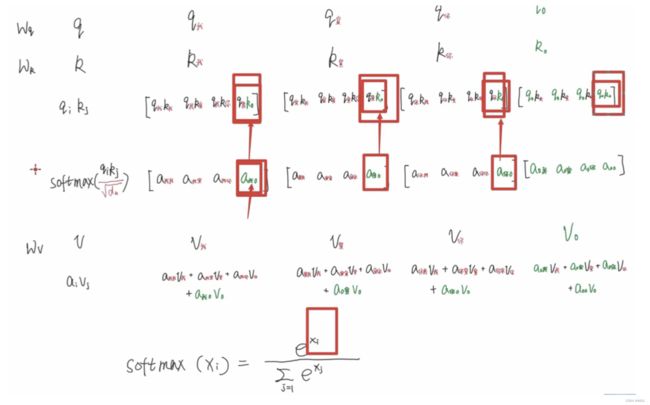
6.1.5 并行化处理（矩阵运算）

其实就是矩阵运算，上述例子为方便起见是向量，下图为对应的矩阵运算：

当然这里还有一个更漂亮的图：

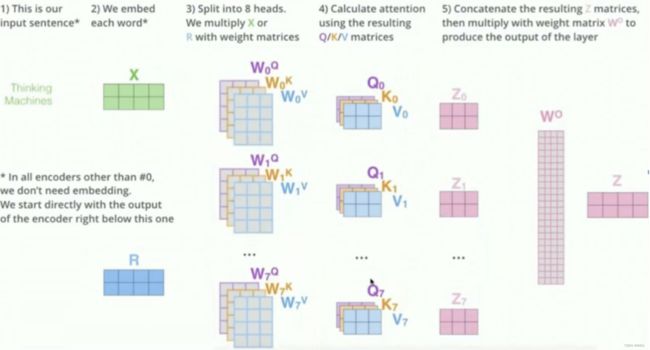
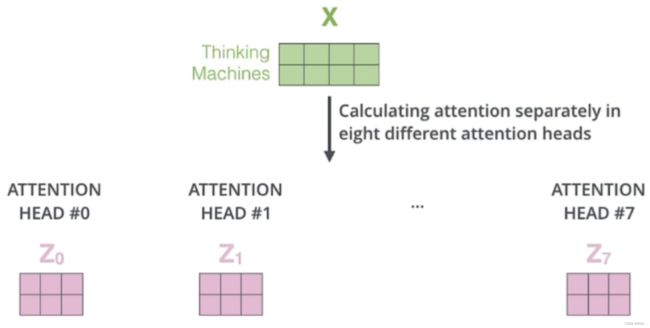
6.1.6 多头 Multi-head

将上面的self-attention弄懂了，多头也就懂一大半了，而encoder和decoder部分是一样的，论文的名字也是attention is all you need，attention就是精华。

理论上，多头指的就是多套Q、K、V。比如论文原文是8个头，那就是8套Q、K、V。

• 多套参数相当于把原始信息放到了多个空间中，也就是捕捉了多个信息，多头保证了transformer可以注意到不同子空间的信息，能够捕捉到更加丰富的特征信息。
• 换句话说就是经过注意力之后的矩阵会有自己理解的语义信息，那所以最后8个Z就会有8个不同的理解。

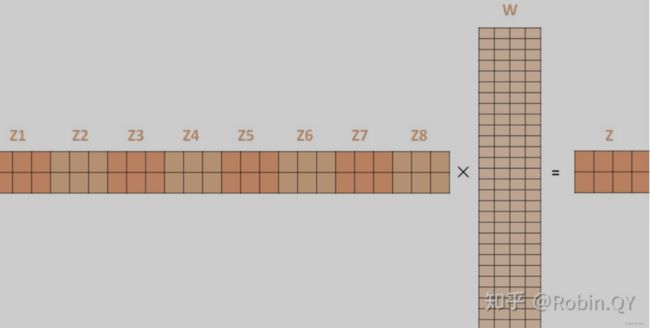
多个头就会有多个输出：

多头信息输出，由于多套参数得到了多个信息，然而我们还是只需要一个信息，因此可以通过某种方法(例如矩阵相乘)把多个信息汇总为一个信息:

看过源码的小伙伴会发现实际上我们并不会这么干

如果按照上面的方法，那么8个头就需要8套$W$，但是一套$W$包含了$W_Q、W_K、W_V$，这样的话训练开销会非常大，并且线上推断的时间也会很长。

所以实际用的时候，我们会将矩阵按照头数来进行切分，比如下面例子是2个头

• 首先生成Q、K、V，比如是2个头，那就将Q拆成2个部分。

• 也就是说只用一套$W_Q、W_K、W_V$参数来生成$Q、K、V$，然后在此基础之上进行拆分。

• 假如Q的维度是（seq_len, d_model），分别代表句子长度和emb维度；
• 如果是两个头的话，就按中间分一刀，左面是一个头$q_1$，右面是一个头$q_2$；
  • 需要注意的是：emb的维度一定要整除要分的头数 。

• 然后就是各自的头干各自的事情，分头行动；
• 然后分别去做缩放点击运算；
• 做完之后，如上图，可以看到左面是第一个头的语义信息，右面是第二个头的语义信息；

• 将多个头的结果拼接起来，还原到之前的维度；
• 这样就相当于从多个头当中提取到的特征都给融合到了一起。

上面的图例为了方便演示，下图为实际分头的图例，
假设inpt维度为（batch_size, seq_len, d_model）=（2, 6, 4）
分成两头之后维度为（batch_size, head_num, seq_len, depth）=（2， 2， 6， 2）

6.1.7 为什么要使用多头注意力？

前面也简单的提到了一点，这里总结下，加深理解：

• 多头保证了transformer可以注意到不同子空间的信息，捕捉到更加丰富的特征信息。
• 论文作者发现这样做效果缺失好。
• 捕捉到特征的多样性，说人话就是”因为有多头，所以可以从多个⻆度去理解内容“。 举个例子来理解的话:
  • 学姐查寝
  • 它可以理解为:学姐-查寝
  • 也可以理解为:学-姐-查寝
• 通过多头注意力可以充分的解读上下文的语义信息，换句话说就是充分的带入到一个场景中去做理解。

6.1.8 Padding mask

简单说padding mask的作用就是标记padding项的位置。

目的是消除padding项带来的影响。

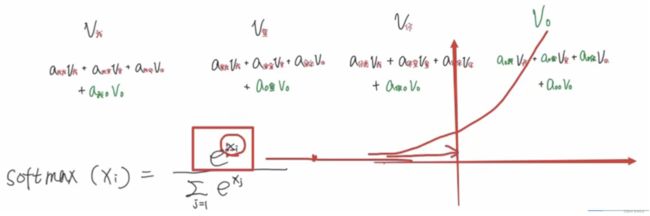
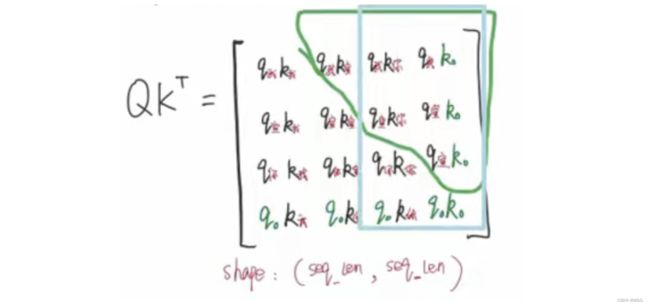
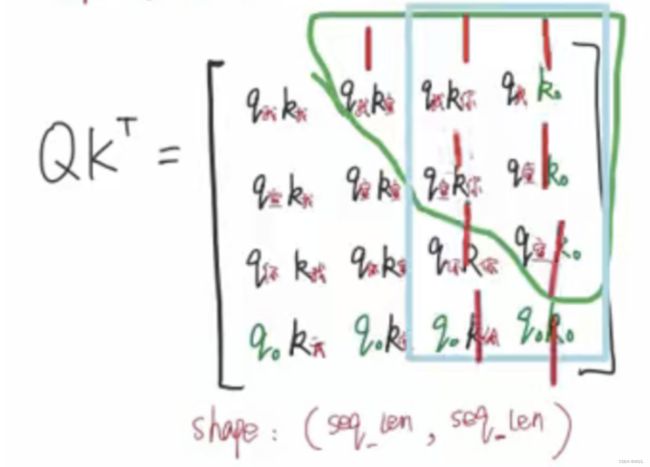
我们先回到上面attention的例子中，在最后加了padding项，看会有怎样的影响：

绿色部分就是和padding相关的

• Q、K、V的生成是没有问题的，padding项也需要Q、K、V。
• QK相乘也是没有问题的。只要padding不影响有效信息的运算就好了。
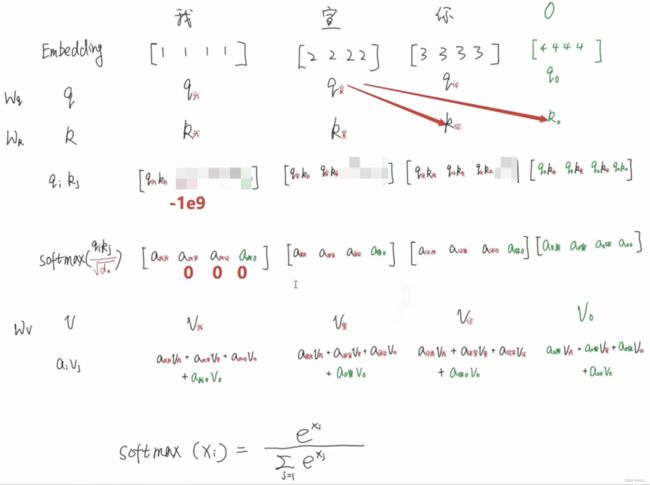
  • 比如在执行QK相乘的时，以”我“为例，不影响$q_{我}{k}_{我}、q_{我}{k}_{宣}、q_{我}{k}_{你}$的运算。只多了个padding，它不会影响其它项的生成。
• 当执行softmax这里的时候，就有问题了:
  • 由softmax公式得知
    $$softmax(x_i)=\frac{e^{x_i}}{{\sum }_{i=1}{e}^{x_i}}$$
  • 当执行softmax的时候，padding项作为$x_i$也会参与softmax的运算；
  • 这样一来就相当于绿色的部分也会生成权重！

• 比如上图，它会认为”我“和padding存在某种联系，这是不合理的。因为padding本身就是没有意义的， 只是我们的填充项而已。
• 所以要将这些部分变成0。
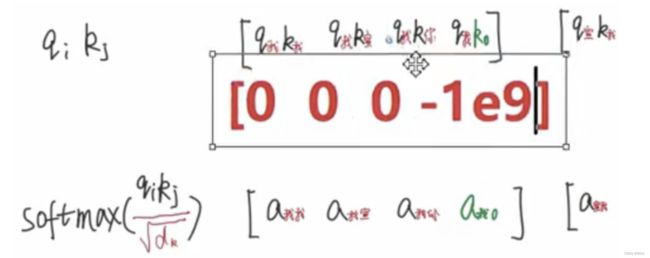
• 所以往上走就要在QK相乘的地方就要把有padding的变成0，即在softmax运算之前就要把含padding的给处理掉。

• 这时就用到了padding mask: 将padding项变成1，其它项变成0。
• 当走到QK运算的时候，就可以通过1来定位到padding的部分。

• 这里为什么不将padding项变为0，然后和QK的结果相乘?

  • 它产生影响只是在softmax的时候有影响，使得$a_{我0}$产生了值；
  • 如果将padding项变为0，然后和QK相乘的话，那么$q_{我}{k}_0$的结果为0；
  • 计算softmax的时候，$e^0$是1，也就是生成的$a_{我0}$依然是一个不为0的值，没有办法消除掉；
  • 所以$q_{我}{k}_0$等于0是没有意义的。

• 我们不会让它们相乘，是让它们相加，我们会让1变成一个非常小的数，比如$-10^9$。

• 相加之后，和padding项有关的值会变成一个非常小的数。其他的部分因为加的是0所以不会改变。我们做的事情就是把和padding有关的项变成一个极其小的数。

• 当$x_i$非常非常小的时候，$e^{x_i}$会无限接近于0，就可以近似的看成0来看待。
• 最后的a就会变成0，从而将padding产生的影响消除掉。

• 至于蓝色部分，padding项的QK等于多少都无所谓，因为它不影响前面的计算。
• padding项的a是0，那么和V相乘的时候也是0，即$a_{我0}{V}_0=0$，就相当于没有从padding项提取到任何信息。

至此，padding mask讲完了，它的作用就是将padding产生的影响给消除。

6.2 Add&Norm

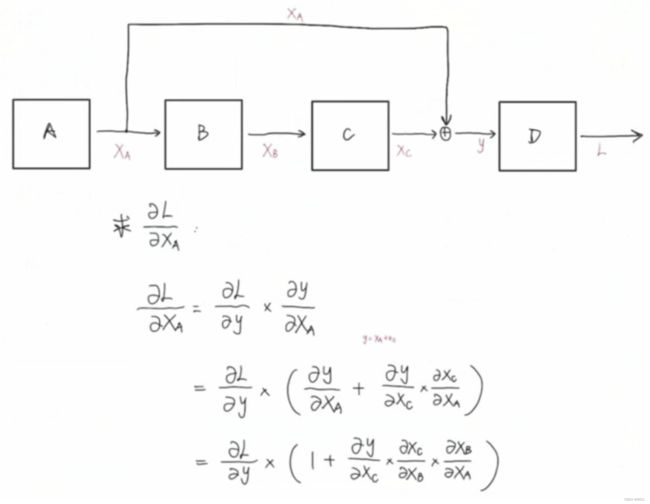
6.2.1 Add（Skip Connection）

Add部分没什么好讲的，就是残差网络的跳跃连接思想。

作用就是加深网络层数，通过跳跃连接缓解梯度消失。

• 因为$y=x_A+x_C$，所以$\frac{\partial y}{\partial x_A}=1$；
• 缓解了梯度消失，不管连乘项有多少，前面至少还有一个1，可以保证梯度回传，即$\frac{\partial y}{\partial x_A}$不为0。

6.2.2 什么是BatchNorm？

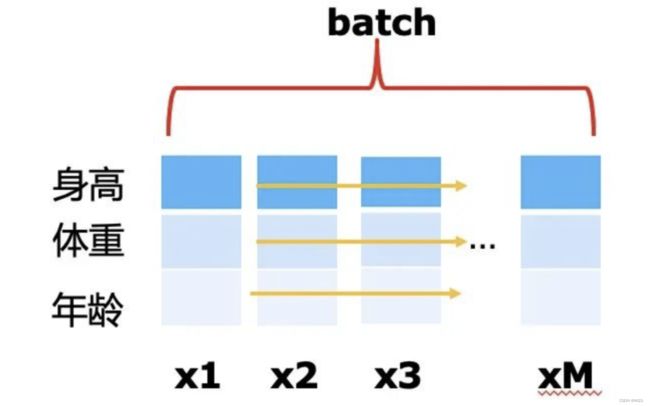
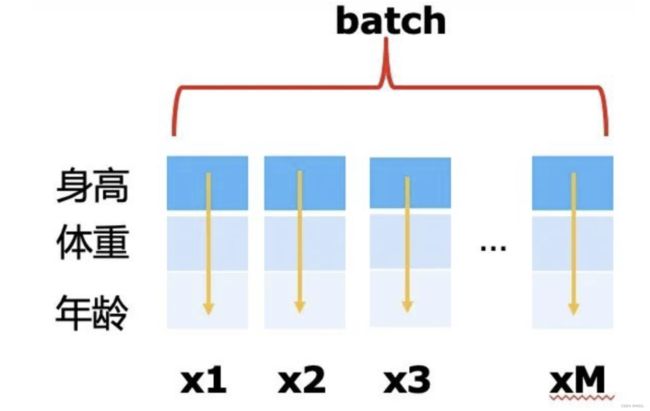
• BatchNorm是对一批样本进行处理,对一批样本的每个特征分别进行归一化。
• 举个简单的例子,假如我有一批样本,每个样本有三个特征,
  • 分别是身高,体重,年龄,那么我做归一化的时候,就是对体重做归一化,对身高做归一化,对年龄做归一化,
  • 三者之间不会有交叉影响。

• 这个看起来很符合直观的感觉,可以看做是降低每个特征量纲的影响,我们也经常会在CTR等深度模型的MLP部分见到BatchNorm操作。
• 也正因为如此,
  • 所以BatchNorm会受到Batch size的影响;
  • 当Batchsize小的时候效果往往不是非常稳定.

6.2.3 什么是LayerNorm？

• LayerNorm是对一个样本进行处理,
• 对一个样本的所有特征进行归一化,乍一看很没有道理,
• 因为如果对身高体重和年龄一起求一个均值方差,都不知道这些值有什么含义,但存在一些场景却非常有效果–NLP领域。

• 在NLP中,N个特征都可能表示不同的词,这个时候我们仍然采用BatchNorm的话,对第一个词进行操作,很显然意义就不是非常大了,
• 因为任何一个词都可以放在第一个位置，而且很多时候词序对于我们对于句子的影响没那么大，
• 而此时我们对N个词进行Norm等操作可以很好地反映句子的分布。
• (LN一般用在第三维度,[batchsize,seq_len,dims]),因为该维度特征的量纲是相同的,所以并没有太多区别。

6.2.4 为什么使用LayerNorm，不用BatchNorm？

上面其实就已经给出讲解了，这里再接着上面的例子加深理解：

LayerNorm简称LN，BatchNorm简称BN。
它俩的作用都是消除量纲影响，加快模型收敛。

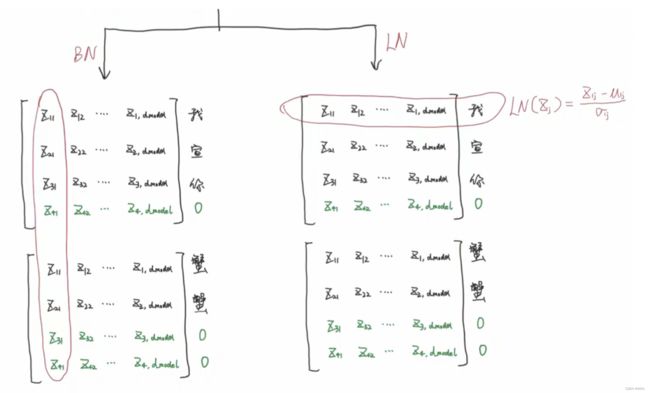
• BN做的事情是将这个batch内的，对每个特征分别求均值、标准差，然后再各自减去均值除以标准差。从而让分布变到均值为0，方差为1的标准正太分布当中。
• LN是以样本为单位去计算均值和标准差的。

• 在nlp领域使用BN效果不好，BN的计算方式是以一个batch中的样本数据去计算它的均值和方差的。
  • 这样计算它是有padding的影响的，并且代表不了整个的均值和方差。在刚刚小明和小红例子中，身高这个特征所在的列含义是相同的。但是在nlp里，第一行是”我“字的emb词向量，第二行是”宣“字的emb词向量，经过attention之后，形成的是包含语义信息的向量，每一列代表的含义并不相同了。
• 不能说每个词向量的每个维度代表的含义是一样的。
• 因此从这个⻆度来理解，这里采用BN是不合适的。
• 所以LN用的是比较多的。以每个词向量去做标准化就可以了，这样就不会引入padding不相关的信息。
• batch_size太小时，一个batch的样本，其均值和方差，不足以代表总体样本的均值与方差。NLP领域不适合用BN。

6.3 前馈神经网络（Feed Forword）

这里也是没什么好讲的，就是一个两层的全连接。通过激活函数引入非线性变换，变换了Attention output的空间, 从而增加了模型的表现能力。

把FFN去掉模型也是可以用的，但是效果差了很多。

七、Decoder部分

encoder和decoder结构相似，只需要关注decoder部分的attention就可以了，其它的就不再赘述了。

其中Decoder部分可以分为2个讲解：

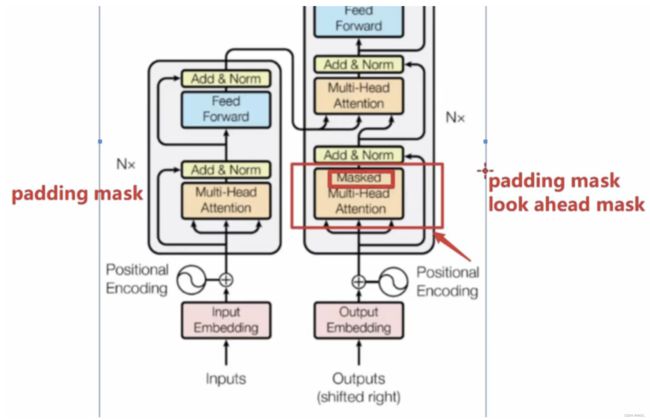
• Masked Multi-Head Attention
  • 带mask的多头注意力机制，目的是为了防止模型看到要预测的数据，防止泄露。
  • 如果不清楚的同学，可以往上翻，看下机器翻译工作流程的Decoder部分。
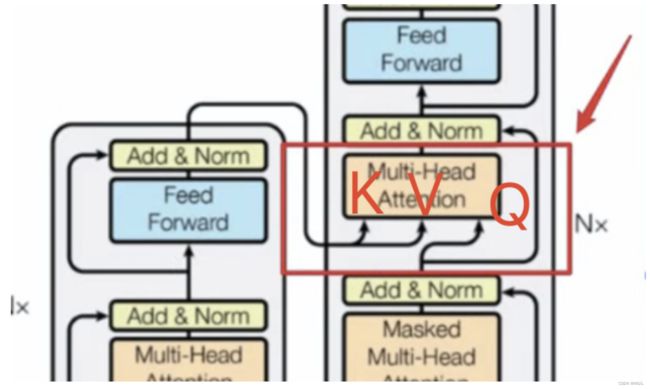
• Encoder-Decoder Multi-Head Attention
  • 用于Encoder部分和Decoder部分的交互。
  • 细心的同学可以看到这里的箭头有两个是来自Encoder，有一个是来自Decoder。

7.1 带mask的多头注意力机制（Masked Multi-Head Attention）

Encoder和Decoder部分都有padding mask，在Decoder部分还多了一个look ahead mask，就是masked Multi head attention的mask的含义。

篇幅太长了，我不想分两篇写，所以这里先回顾一下decoder部分的工作流程：

• 首先是预测第一个位置，图中红框，要保证第一个位置的预测只和起始符start有关，所以要把start后面的部分给遮盖掉。

• 预测第二个位置的时候，要保证第二个预测位置只和start、I有关，所以后面的部分要mask掉。
• 很好理解，就是根据前面的信息，预测可能出现的下一个值。

假设这是decoder部分的多头注意力，我们来看一下如果不做mask会是什么样：

• 如果不使用mask，在qk的时候，”我“字还会和其它字交互，但是decoder在预测出”宣“的时候，是看不到后面的信息的。

• 所以$q_{我}{k}_{宣}、q_{我}{k}_{你}、q_{我}{k}_0$是不合理的，要mask掉。
• 如果这么值没有被mask，那么它会在softmax的时候产生值，对$a_{我我}$产生影响。
• 同理，"宣"、“你”和padding项产生的交互都要被mask。

padding项不会对前面的计算产生影响所以不用考虑

• 这里掩盖和padding mask哪里是一样的处理，会给一个很小的数 $-10^9$；
• 所以现在的问题又转变成了如何去定位这些需要mask的位置；
• 它其实是一个倒三⻆的形状，分别是3个需要mask、2个需要mask、1个需要mask。

• 在矩阵里，它就是如上图的样子，第一行有3个需要被mask、第2行有2个需要被mask、第3行有1个需要被mask。 是一个倒三⻆的形状。

• 所以look ahead mask的生成，只要将需要掩盖的地方为1，其它不需要掩盖的地方为0即可。

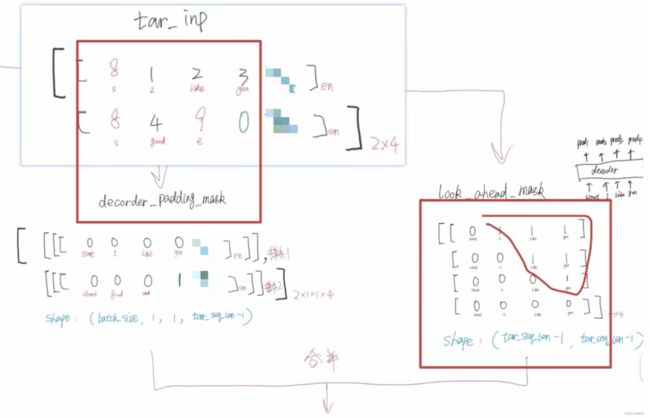
• 同时我们还要考虑之前的padding mask，打个比方:

• 假设”你“也是padding项，那么和padding有关的将用绿色表示 ；
  • 倒三⻆里的都会被mask掉。
• 同时我们还要将padding mask给考虑进去；
• 这个时候，在矩阵里的padding mask，就是最后两列，下图：

• 我们要做的是处理它们的并集，如果只处理倒三⻆的话，那么最后两列中，除倒三⻆之外的地方就被忽略了，如图 $q_{我}{k}_{你}、q_0{k}_{你}、q_0{k}_0$；
• 这些地方就是和padding相关的，需要用到padding mask来处理。
• 换句话说，如果只看padding mask的话，那么除了最后两列padding mask的部分之外也没办法处理，如图 $q_{我}{k}_{宣}$，它是look ahead mask处理的部分。

• 所以我们要做的是计算它们的并集，即生成的掩码为1的部分如图，其它部分为0。
• 这样就能把padding和提前预⻅的负面情况带来的消极影响给消除掉。

• 首先要定位到padding mask，同时生成一个look ahead mask。
• look ahead mask的生成和padding也没有关系，只需要知道句子的⻓度即可，先生成方阵，再变成倒三⻆。 然后再求一个并集，变成下面这个样:

这里涉及到自动广播，不明白的同学可以自行查阅，此处不再介绍。

Decoder的多头注意力和Encoder的多头注意力的不同地方就在于使用的mask不同。

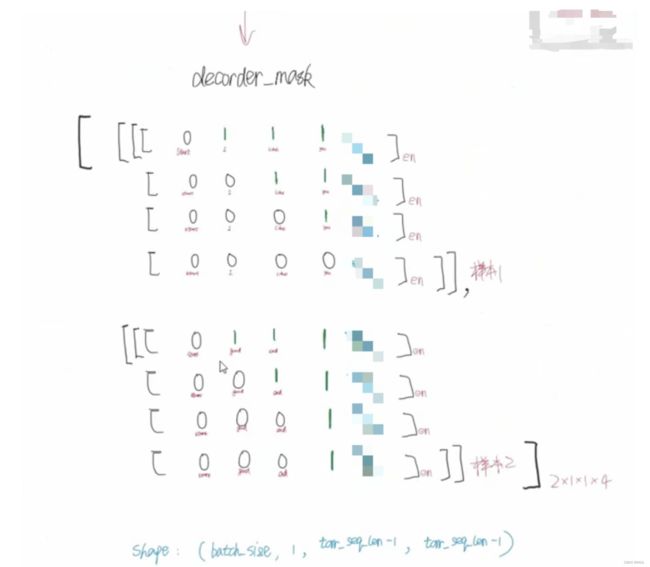
7.2 Encoder与Decoder间的多头注意力机制（Multi-Head Attention）

我们发现，其它多头注意力的Q、K、V是来自同一个的。但是在红框的Q、K、V的来源就不再是同一个东西了。

• 它的Q是Decoder部分Add&Norm之后的线性变换。
• K、V是Encoder部分的输出经过线性变换得到的。
• 同时也会有padding mask去处理padding部分，和Encoder部分的padding mask一致。

我们来通过下图例子理解：

需要说明的是，
例子中不包含起始符和结束符
padding项都是绿色
q是decoder部分提供、k和v是encoder部分输出

• 计算qk，以$q_I$为例:

  • 可以理解为两种不同语言之间相关性的交互，这就是翻译的效果。
  • 换句话说之前注意力计算是”我宣你“这句话之间的计算，计算每个单词和其它单词的相关性。
  • 这里因为q是来源于Decoder部分，以$q_I$为例，qk计算的是”I“分别和”我“、”宣“、”你“的相关性。

• 经过softmax将得分归一化，映射成注意力权重。

• 然后和v相乘，含义也是一样的，从”我“、”宣“、”你“中提取多少信息。

• 这样一来通过不同语言间相关性的匹配就能从中提取出翻译的信息，达到一个翻译的效果。

• 为什么这里的padding mask和encoder部分的padding mask处理方法一致？

  • 看上图的qk结果，每个词向量的padding影响都是最后一个，也就是说影响来自于$k_0$，即Encoder部分的输出k。
  • 所以要消除这里的影响，就要以Encoder部分为基准来生成padding mask。

• 也是用1代表padding项，0代表其它项的方式来定位padding项。
• 具体处理手法也是一样的，在softmax之前，给padding项加一个很小的数，如下图。

这里可能会有疑问，为什么这里使用padding mask，而不使用look ahead mask？

• 在输入起始符s的时候，I就是预测的目标。这个时候s后面的这些是还没有生成的，所以要遮盖掉。

• 所以当qk计算的时候，还是以“我”字为例，“宣”、“你”，都还没有出现，所以$q_{我}{k}_{宣}、q_{我}{k}_{你}$是不合理的。

• 因为还没有生成，所以需要mask掉，如下图所示：

• 而在这里，做的注意力机制是Encoder和Decoder之间的交互

• 我们可以发现，I询问的对象（$q_I$），全都是中文部分，即“我”、“宣”、“你”。
• 换句话说，对于q而言，k都是可见的，因为它是由Encoder部分直接给过来的。
  • 即Encoder部分传过来的，对于Decoder部分而言都是可见的。
• 所以不需要做look ahead mask了，只需要针对Encoder部分做一个padding mask。

坚持看到这里的小伙伴相信肯定是收获满满，动动发财的小手关注博主一波，一起进步。

八、输出部分

以上就讲完了transformer的编码、解码两大模块，那么如何将“我喜欢你”，翻译成“I Like You”呢？

换个问题，解码器Decoder输出本来是一个浮点型的张量，怎么转化成“I Like You”这几个词呢？

概况的来讲：

• 最后的输出要通过Linear层（全连接层），它将Decoder产生的向量投影到一个更高维度的向量上（logits）；
• 假如我们的词汇表有1W个词，那么这个 logits 就有1W个维度，每个维度对应一个唯一的词的得分；
• 之后经过softmax将这么分数转为概率；
• 选择概率最大的维度，并对应地生成与之关联的单词作为时间步的输出就是最终的输出了。

九、有关训练

9.1 损失计算

损失依旧是交叉熵，为什么这里会讲一下，因为有padding。

也就是说我们需要注意的是，损失计算也要有mask，去消除padding项带来的损失。

在计算损失的时候，需要做：

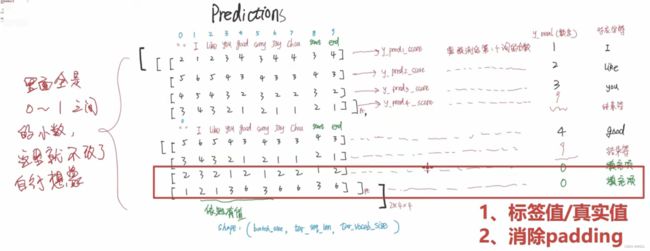
• 先拿到标签值（真实值）。
• 消除padding带来的影响。

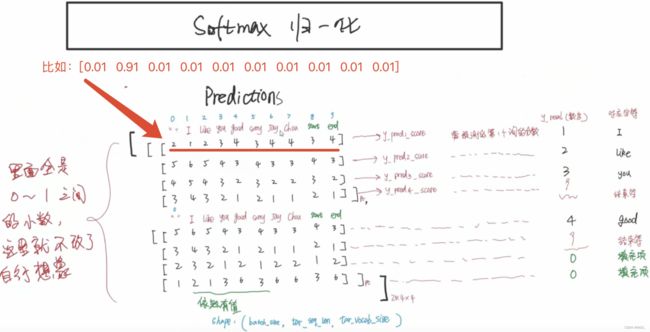
Predictions矩阵，是经过softmax后的预测概率值

• 我们不应该将padding项带来的损失，加到整体的损失里面。
• 因此需要mask去消除掉。

• 与之前不一样的是，这里的padding项直接按0来处理，非padding项按1来处理。
• 然后将标签和mask对应元素相乘即可。
  • 如果不mask的话，padding项也会产生损失，padding只是填充项，没有实际的意义。

9.2 自定义学习率

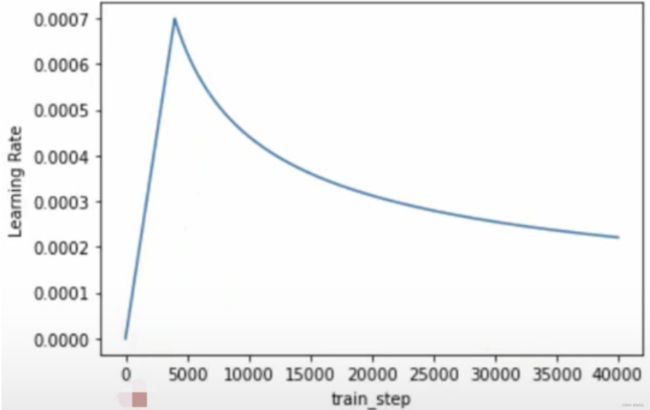
这是论文中提到的一种自定义学习率方法：

• d_model：emb维度
• step_num：当前训练走到了第几步
• warm_up_steps：为自定义的一个值

最后的效果就是一个先增后减的学习率（和学习率衰减思想一致）

十、全部代码及资料

https://github.com/WGS-note/transformer-note

如果觉得文章还不错，读完后收获颇丰，动动小伙伴发财的小手帮博主start一下~

References

https://s3.us-west-2.amazonaws.com/secure.notion-static.com/501fb338-a6b0-484a-8a16-713dd40251de/Attention_is_All_You_Need.pdf?X-Amz-Algorithm=AWS4-HMAC-SHA256&X-Amz-Content-Sha256=UNSIGNED-PAYLOAD&X-Amz-Credential=AKIAT73L2G45EIPT3X45%2F20220522%2Fus-west-2%2Fs3%2Faws4_request&X-Amz-Date=20220522T014504Z&X-Amz-Expires=86400&X-Amz-Signature=180db501219c968fdd116b27d6b44bed0eed6e912755d300cd7db8e957937e1b&X-Amz-SignedHeaders=host&response-content-disposition=filename%20%3D%22Attention%2520is%2520All%2520You%2520Need.pdf%22&x-id=GetObject

https://ugirc.blog.csdn.net/article/details/120394042

https://luweikxy.gitbook.io/machine-learning-notes/self-attention-and-transformer#multi-headed-attention

https://zhuanlan.zhihu.com/p/353381965

https://www.bilibili.com/video/BV1pu411o7BE?spm_id_from=333.337.search-card.all.click

https://www.bilibili.com/video/BV1Kq4y1H7FL?spm_id_from=333.337.search-card.all.click

https://zhuanlan.zhihu.com/p/153183322

---

---

---

原创不易，转载请注明出处