数学建模算法与应用 线性规划（cvxpy包）

数学建模算法与应用 线性规划（使用cvxpy包）

说明

• 使用python中cvxpy库完成《数学建模算法与应用》中课后习题

• 因为本人也是初学者，若代码有错误还请各位指出

cvxpy库的使用

• 这里以简单例子来使用cvxpy库

$$maxz=4x_1+3x_2$$

$$s.t.=\{\begin{array}{l}2x_1+x_2\le 10\\ x_1+x_2\le 8\\ x_2\le 7\\ x_i\ge 0\end{array}$$

import cvxpy as cp
import numpy as np
# 决策变量
n = 2
# cvxpy使用cp.Variable(n,intger = True)中的intger参数来规定x变量为整数
x = cp.Variable(n, integer=True)

# 约束1
A1 = np.array([[2,1],
             [1,1],
             [0,1]])
b1 = np.array([10,8,7])

# 约束2
A2 = np.array([[1,0],
             [0,1]])
b2 = np.array([0,0])

# 目标函数
c = np.array([4, 3])
# 将最大化目标变为最小化
c = -c

# 定义问题，添加约束条件
prob = cp.Problem(cp.Minimize(c.T @ x),
                  [A1 @ x <= b1, A2 @ x >= b2])

# 求解
ans = -round(prob.solve(solver = cp.ECOS_BB))

# 输出结果
print("目标函数最大值:", ans)
# 对x向量各元素取整数后再输出
value = []
for item in x.value:
    value.append(round(item))
print(value)

输出：

目标函数最大值: 26
[2, 6]

习题

习题1.1

$$maxz=3x_1-x_2-x_3$$

$$s.t.=\{\begin{array}{l}{x}_1-2x_2+x_3\le 11\\ -4x_1+x_2+2x_3\ge 3\\ -2x_1+x_3=1\\ x_i\ge 0\end{array}$$

import cvxpy as cp
import numpy as np
# 决策变量
n = 3
x = cp.Variable(n, integer=False)

# 约束1
A1 = np.array([1, -2, 1])
b1 = np.array([11])

# 约束2
A2 = np.array([-2, 0, 1])
b2 = np.array([1])

# 约束3
A3 = np.array([[-4, 1, 2],
               [1, 0, 0],
               [0, 1, 0],
               [0, 0, 1]])
b3 = [3, 0, 0, 0]

# 目标函数
c = np.array([3, -1, -1])
c = -c
# 定义问题，添加约束条件
prob = cp.Problem(cp.Minimize(c.T @ x),
                  [A1 @ x <= b1, A2 @ x == b2, A3 @ x >= b3])

# 求解
ans = -round(prob.solve(solver=cp.ECOS_BB))

# 输出结果
print("目标函数最大值:", ans)
# 对x向量各元素取整数后再输出
print(x.value)

输出：

目标函数最大值: 2
[4. 1. 9.]

习题1.2

$$minz=|x_1|+2|x_2|+3|x_3|+4|x_4|$$

$$s.t.=\{\begin{array}{l}{x}_1-x_2-x_3+x_4=0\\ x_1-x_2+x_3-3x_4=1\\ x_1-x_2-2x_3+3x_4=-0.5\end{array}$$

• 做变量变换$u_i=\frac{x_i+|x_i|}{2}$,$v_i=\frac{|x_i|-x_i}{2}$，将模型变换为线性规划模型

$$min{c}^T(u+v)$$

$$s.t.=\{\begin{array}{l}A(u-v)\le b\\ u,v\ge 0\end{array}$$

import cvxpy as cp
import numpy as np
# 决策变量
n = 4
u = cp.Variable(n, integer=False)
v = cp.Variable(n, integer=False)

# 约束1
A1 = np.array([[1, -1, -1, 1],
              [1, -1, 1, -3],
               [1, -1, -2, 3]])
b1 = np.array([0, 1, -0.5])

# 约束2
A2 = np.ones((4, 4))
for i in range(A2.shape[0]):
    for j in range(A2.shape[1]):
        if i == j:
            pass
        else:
            A2[i, j] = A2[i, j]*0

b2 = np.array([0, 0, 0, 0])

# 目标函数
c = np.arange(1, 5, 1)

# 定义问题，添加约束条件
prob = cp.Problem(cp.Minimize(c.T @ (u+v)),
                  [A1 @ (u-v) == b1, A2 @ u >= b2, A2 @ v >= b2])

# 求解
ans = prob.solve(solver=cp.ECOS_BB)

# 输出结果
print("目标函数最小值:", ans)
# 对x向量各元素取整数后再输出
print(u.value - v.value)

print(A2)

输出：

目标函数最小值: 1.25
[ 2.50000000e-01 -2.97320702e-11  2.28691875e-11 -2.50000000e-01]

习题1.3

   某厂生产三种产品Ⅰ、Ⅱ、Ⅲ。每种产品要经过$A$、$B$两道工序加工。设该厂有两种规格的设备能完成$A$工序，它们以$A_1,A_2$表示；有三种规格的设备能完成B工序，它们以$B_1$、$B_2$、$B_3$表示。产品Ⅰ可在$A$、$B$任何一种规格设备上加工。产品Ⅱ可在任何规格的$A$设备上加工，但完成$B$工序时，只能在$B_1$设备上加工；产品Ⅲ只能在$A_2$和$B_2$设备上加工。已知在各种机床设备的单件工时、原材料费、产品销售单价、各种设备有效台时以及满负荷操作时机床设备的费用如表所示，求最优的生产计划，使该厂利润最大。

算法设计

   对产品Ⅰ来说，设以$A_1,A_2$完成$A$工序的产品分别为$x_1$、$x_2$件，转入$B$工序时，以$B_1$、$B_2$、$B_3$完成$B$工序的产品分别为$x_3$、$x_4$、$x_5$件；对产品Ⅱ来说，设以以$A_1,A_2$完成$A$工序的产品分别为$x_6$、$x_7$件，转入$B$工序时，以$B_1$完成$B$工序的产品为$x_8$件；对产品Ⅲ来说，设以$A_2$完成$A$工序的产品为$x_9$，则以$B_2$完成$B$工序的产品也为$x_9$件。

$$\begin{array}{rl}maxz& =(1.25-0.25)(x_1+x_2)+(2-0.35)x_8+(2.8-0.5)x_9\\ & -\frac{300}{600}(5x_1+10x_6)-\frac{321}{10000}(7x_2+9x_7+12x_9)\\ & -\frac{250}{4000}(6x_3+8x_8)-\frac{783}{7000}(4x_4+11x_9)-\frac{200}{400}\times 7x_5\end{array}$$

$$s.t.=\{\begin{array}{l}5x_1+10x_6\le 6000\\ 7x_2+9x_7+12x_9\le 10000\\ 6x_3+8x_8\le 4000\\ 4x_4+11x_9\le 7000\\ 7x_5\le 4000\\ x_1+x_2=x_3+x_4+x_5\\ x_6+x_7=x_8\\ x_i\ge 0,i=1,2,...,9\end{array}$$

# 决策变量
n = 9
x = cp.Variable(n, integer=True)

# 约束1
A1 = np.array([[5,0,0,0,0,10,0,0,0],
               [0,7,0,0,0,0,9,0,12],
               [0,0,6,0,0,0,0,8,0],
               [0,0,0,4,0,0,0,0,11],
               [0,0,0,0,7,0,0,0,0]])
b1 = np.array([6000,10000,4000,7000,4000])

# 约束2
A2 = np.ones((9, 9))
for i in range(A2.shape[0]):
    for j in range(A2.shape[1]):
        if i == j:
            pass
        else:
            A2[i, j] = A2[i, j]*0

b2 = np.array([0,0,0,0,0,0,0,0,0])

#约束3
A3=np.array([[1,1,-1,-1,-1,0,0,0,0],
            [0,0,0,0,0,1,1,-1,0]])
b3=np.array([0,0])

# 定义问题，添加约束条件
prob = cp.Problem(cp.Maximize(x[0] + x[1] + 1.65 * x[7] + 2.3 * x[8] - 0.05 * (5 * x[0] + 10 * x[5])-
                              0.0321 * (7 * x[1] + 9 * x[6] + 12 * x[8])-25/400 * (6 * x[2] + 8 * x[7])-
                              783/7000 * (4 * x[3] + 11 * x[8])-0.35 * x[4]),
                  [A1 @ x <= b1, A2 @ x >= b2, A3 @ x == b3])

# 求解
ans = prob.solve(solver=cp.ECOS_BB)

# 输出结果
print("目标函数最大值:", ans)
# 对x向量各元素取整数后再输出
print(x.value)

输出：

目标函数最大值: 1146.4142000003724
[ 1.20000000e+03  2.30000000e+02  1.73068974e-09  8.59000000e+02
  5.71000000e+02 -1.28932697e-09  5.00000000e+02  5.00000000e+02
  3.24000000e+02]

习题1.4

   一架货机有三个货舱：前舱、中舱和后舱。三个货舱所能装载的货物的最大质量和体积有限制。为了飞机的平衡，三个货舱装载的货物质量必须与其最大的容许量成正比例。现有四类货物用该货机进行装运，货物的规格以及装运后获得的利润如表所示。

• 每种货物可以无限细分；

• 每种货物可以分布在一个或者多个货舱内；

• 不同的货物可以放在同一个货舱内，并且可以保证不留空隙。

   如何装运，使货机飞行利润最大

算法设计

   用$i=1,2,3,4$分别表示货物1、货物2、货物3、货物4；$j=1,2,3$分别表示前舱、中舱和后舱。设$x_{ij}(i=1,2,3,4;j=1,2,3)$表示第$i$种货物装在第$j$个货舱内的质量，$w_j,v_j(j=1,2,3)$分别表示第$j$个舱的质量限制和体积限制，$a_i,b_i,c_i(i=1,2,3,4)$分别表示可以运输的第$i$种货物的质量，单位质量所占的空间和单位货物的利润。

$$maxz=\sum _{i=1}^4{c}_i\sum _{j=1}^3{x}_{ij}$$

$$s.t.=\{\begin{array}{l}\sum _{j=1}^3{x}_{ij}\le a_i,i=1,2,3,4\\ \sum _{i=1}^4{x}_{ij}\le w_i,j=1,2,3\\ \sum _{i=1}^4{b}_i{x}_{ij}\le v_i,i=1,2,3\\ \frac{\sum _{i=1}^4{x}_{i1}}{10}=\frac{\sum _{i=1}^4{x}_{i2}}{16}=\frac{\sum _{i=1}^4{x}_{i3}}{8}\\ x_{ij}\ge 0,i=1,2,3,4;j=1,2,3\end{array}$$

• 此次在变量设定中使用了nonneg参数规定$x_{ij}$非负，可以不用写最后一条约束

• 涉及到变量求和的地方使用cvxpy包中内置sum函数，即cp.sum()

• 更多内置函数参考cvxpy官方文档

# 决策变量
n = (4,3)
# nonneg参数，变量是否为非负
x = cp.Variable(n,nonneg = True)

# 约束1
b1 = np.array([18,15,23,12])

# 约束2
b2 = np.array([10,16,8])

# 约束3
A3 = np.array([480,650,580,390])
b3 = np.array([6800,8700,5300])
# 定义问题，添加约束条件
c = np.array([3100,3800,3500,2850])
prob = cp.Problem(cp.Maximize(c @ cp.sum(x,axis = 1)),
                  [cp.sum(x,axis = 1) <= b1,
                   cp.sum(x,axis = 0) <= b2,
                   A3 @ x <= b3,
                  cp.sum(x[:,0])/10 == cp.sum(x[:,1])/16,
                  cp.sum(x[:,1])/16 == cp.sum(x[:,2])/8])

# 求解
ans = prob.solve(solver=cp.ECOS_BB)

# 输出结果
print("目标函数最大值:", ans)
# 对x向量各元素取整数后再输出
print(np.sum(x.value,axis = 1))

输出：

目标函数最大值: 121515.7894845719
[3.19620414e-08 1.50000000e+01 1.59473684e+01 3.05263157e+00]

习题1.5

   某部门在今后五年内考虑给下列项目投资，已知：

   项目A，从第一年到第四年每年年初需要投资，并于次年末回收本利115%；

   项目B，从第三年初需要投资，到第五年末能回收本利125%，但规定最大投资额不超过4万元；

   项目C，第二年初需要投资，到第五年末能回收本利140%，但规定最大投资额不超过3万元；

   项目D，五年内每年初可购买公债，于当年末归还，并加利息6%。

   该部门现有资金10万元，问它应如何确定给这些项目每年的投资额，使到第五年年末拥有的资金的本利总额最大。

算法设计

   用$j=1,2,3,4$,分别表示项目$A$、$B$、$C$、$D$，用$x_{ij}(i=1,2,3,4,5)$分别表示第i年年初给项目$A$、$B$、$C$、$D$的投资额。

$$maxz=1.15x_{41}+1.40x_{23}+1.25x_{32}+1.06x_{54}$$

$$s.t.=\{\begin{array}{l}{x}_{11}+x_{14}=100000\\ x_{21}+x_{23}+x_{24}=1.06x_{14}\\ x_{31}+x_{32}+x_{34}=1.15x_{11}+1.06x_{24}\\ x_{41}+x44=1.15x_{21}+1.06x_{34}\\ x_{54}=1.15x_{31}+1.06x_{44}\\ x_{32}\le 40000\\ x_{23}\le 30000\\ x_{ij}\ge 0,i=1,2,3,4,5;j=1,2,3,4\end{array}$$

• 换了一个求解器，GLOP

# 决策变量
n = (5,4)
# nonneg参数，变量是否为非负
x = cp.Variable(n,nonneg = True)

prob = cp.Problem(cp.Maximize(1.15 * x[3,0] + 1.40 * x[1,2] + 1.25 * x[2,1] + 1.06 * x[4,3]),
                  [x[0,0] + x[0,3] == 100000,
                  x[1,0] + x[1,2] + x[1,3] == 1.06 * x[0,3],
                  x[2,0] + x[2,1] + x[2,3] == 1.15 * x[0,0] + 1.06 * x[1,3],
                  x[3,0] + x[3,3] == 1.15*x[1,0] + 1.06*x[2,3],
                  x[4,3] == 1.15*x[2,0] + 1.06 * x[3,3],
                  x[2,1] <= 40000,
                  x[1,2] <= 30000])

# 求解
ans = prob.solve(solver=cp.GLOP)

# 输出结果
print("目标函数最大值:", ans)
# 对x向量各元素取整数后再输出
print(x.value)

输出：

目标函数最大值: 143750.0
[[34782.60869565    -0.            -0.         65217.39130435]
 [39130.43478261    -0.         30000.            -0.        ]
 [   -0.         40000.            -0.            -0.        ]
 [45000.            -0.            -0.            -0.        ]
 [   -0.            -0.            -0.            -0.        ]]

习题1.6

   食品厂用三种原料生产两种糖果，糖果的成分要求和销售价如表所示。该厂根据订单至少需要生产600kg高级奶糖、800kg水果糖，为求最大利润，试建立线性规划模型求解。

算法设计

   用$i=1,2$分别表示高级奶糖和水果糖，用$j=1,2,3$分别表示原料$A$、$B$、$C$。设$x_{ij}(i=1,2;j=1,2,3)$表示生产第$i$种糖用的第$j$种原料的量，$a_i$表示第$i$种糖果的需求量，$b_j$表示第$j$种原料的可供量。
$$maxz=4x_{11}+12x_{12}+16x_{13}-5x_{21}+3x_{22}+7x_{23}$$

$$s.t.=\{\begin{array}{l}\sum _{j=1}^3{x}_{ij}\ge a_i,i=1,2\\ \sum _{i=1}^2{x}_{ij}\le b_j,j=1,2,3\\ x_{11}\ge 50\%(x_{11}+x_{12}+x_{13})\\ x_{12}\ge 25\%(x_{11}+x_{12}+x_{13})\\ x_{13}\le 10\%(x_{11}+x_{12}+x_{13})\\ x_{21}\le 40\%(x_{21}+x_{22}+x_{23})\\ x_{22}\le 40\%(x_{21}+x_{22}+x_{23})\\ x_{23}\ge 15(x_{21}+x_{22}+x_{23})\\ x_{ij}\ge 0,i=1,2;j=1,2,3\end{array}$$

# 决策变量
n = (2,3)
# nonneg参数，变量是否为非负
x = cp.Variable(n,nonneg = True)
# 约束1
b1 = [600,800]

# 约束2
b2 = [600,750,625]
# cp.sum()中axis = 1按行求和
# cp.sum()中axis = 0按列求和
prob = cp.Problem(cp.Maximize(np.array([4,12,16]) @ x[0,:] + np.array([-5,3,7]) @ x[1,:]),
                  [cp.sum(x,axis = 1) >= b1,
                  cp.sum(x,axis = 0) <= b2,
                  x[0,0] >= 0.5 * cp.sum(x[0,:],axis = 0),
                  x[0,1] >= 0.25 * cp.sum(x[0,:],axis = 0),
                  x[0,2] <= 0.1 * cp.sum(x[0,:],axis = 0),
                  x[1,0] <= 0.4 * cp.sum(x[1,:],axis = 0),
                  x[1,1] <= 0.4 * cp.sum(x[1,:],axis = 0),
                  x[1,2] >= 0.15 * cp.sum(x[1,:],axis = 0)])

# 求解
ans = prob.solve(solver=cp.GLOP)

# 输出结果
print("目标函数最大值:", ans)
# 对x向量各元素取整数后再输出
print(x.value)

输出：

目标函数最大值: 14200.0
[[600. 575.  -0.]
 [ -0. 175. 625.]]

习题1.7

   求解下列线性规划问题，其中矩阵$A=(a_{ij}{)}_{100\times 150}$中的元素$a_{ij}$为$[0,10]$上的随机整数。

$$maxv$$

$$s.t.=\{\begin{array}{l}\sum _{i=1}^{100}{a}_{ij}{x}_i\ge v,j=1,2,...,150\\ \sum _{i=1}^{100}{x}_i=100\\ x_i\ge 0,i=1,2,...,100\end{array}$$

#生成随机数种子，使结果固定
np.random.seed(42)
a = np.random.randint(1, 11, size=(100,150))
# 决策变量
n = np.array([100,1])
# nonneg参数，变量是否为非负
x = cp.Variable(n[0],nonneg = True)
v = cp.Variable(n[1])

# cp.sum()中axis = 1按行求和
# cp.sum()中axis = 0按列求和
prob = cp.Problem(cp.Maximize(v),
                  [a.T @ x >= v,
                  cp.sum(x) == 100])

# 求解
ans = prob.solve(solver=cp.GLOP)

# 输出结果
print("目标函数最大值:", ans)
# 对x向量各元素取整数后再输出
print(x.value)

输出：

目标函数最大值: 538.2560346542277
[-0.         -0.          0.32868907  1.83981903  1.60824063  1.42934412
  2.35357916 -0.          3.38452136 -0.          0.00595007  1.6272227
 -0.          0.56945258 -0.          2.54100266  1.43375965  0.86327997
  2.11702508  2.40072583 -0.          2.52730273 -0.         -0.
  1.13784709 -0.          0.62438124 -0.          0.11470483  2.13261487
 -0.          2.78707508  2.7390843   1.22599971  1.36865498  4.55130819
  3.26987533 -0.         -0.         -0.          4.26209229  1.4377878
  0.20195965  0.63892766  0.13196033 -0.         -0.          1.31807878
  0.75303873  3.36903244 -0.          0.81368899  0.2527292   1.94416655
  1.58858316  0.21577316  1.7780698  -0.         -0.          1.77156009
  0.22421819 -0.          0.94448177 -0.         -0.         -0.
  1.13899834  3.02491754  2.22561055  3.26464305 -0.          1.38916772
  2.06832119 -0.          2.6891509  -0.          0.42024825  1.69604933
 -0.          0.03469465 -0.          2.85642199  2.70167707 -0.
  1.01923824  1.87565017  0.98045756 -0.          0.50588775  1.73655473
 -0.         -0.         -0.          0.06062595 -0.          1.46978614
  1.08026003  1.13403002 -0.         -0.        ]

习题1.8

   设$x_{n+1}=\underset{1\le i\le n}{\max }\{q_i{x}_i\}$，则模型二可以线性化为

$$min{x}_{n+1}$$

$$s.t.=\{\begin{array}{l}{q}_i{x}_i\le x_{n+1},i=1,2,...,n\\ \sum _{i=0}^n(r_i-p_i)x_i\ge k_M\\ \sum _{i=0}^n(1+p_i)x_i=M\\ x_i\ge 0,i=0,1,...,n\end{array}$$

# 决策变量
n = 6
# nonneg参数，变量是否为非负
x = cp.Variable(n,nonneg = True)

# 约束1
A1 = np.array([[0,0.025,0,0,0,-1],
              [0,0,0.015,0,0,-1],
              [0,0,0,0.055,0,-1],
              [0,0,0,0,0.026,-1],
              [-0.05,-0.27,-0.19,-0.185,-0.185,0]])

# 约束2
A2 = np.array([1,1.01,1.02,1.045,1.065,0])
b2 = np.array([1])

# 每轮结果
ANS = []
for k in np.arange(0.05,0.255,0.005):
    b1 = np.array([0,0,0,0,-k])
    prob = cp.Problem(cp.Minimize(x[5]),
                      [A1 @ x <= b1,
                      A2 @ x == b2])
    # 求解
    ans = prob.solve(solver=cp.GLOP)
    ANS.append([ans])
    
    if k >= 0.205 and k<= 0.210:
        print(x.value)

输出：

[-0. 0.30887428  0.51479046  0.1403974   0.01524453  0.00772186]

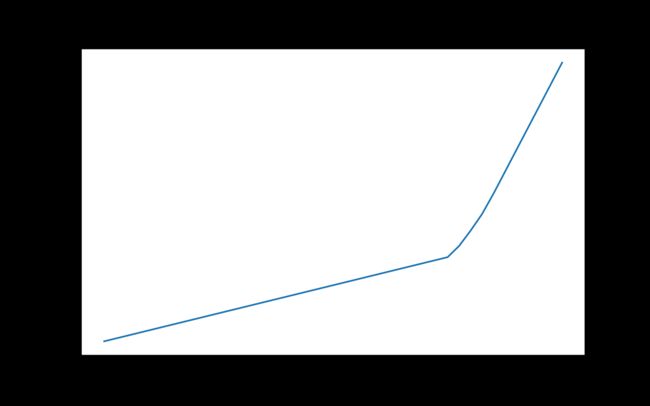
绘制图形观察

import matplotlib as mpl
import matplotlib.pyplot as plt

#中文显示问题
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# notebook嵌入图片
%matplotlib inline
# 提高分辨率
%config InlineBackend.figure_format='retina'

# 忽略警告
import warnings
warnings.filterwarnings('ignore')

plt.figure(dpi = 600,figsize = (5,5))
plt.plot(np.arange(0.05,0.255,0.005),ANS)
plt.xlabel("Profit")
plt.ylabel("Risk")
plt.title("Profit and Risk chart")
plt.savefig("Profit and Risk chart")

结语

   最后这里提供给大家源代码文件