数据结构与算法python—2.顺序表(数组)以及python实现
文章目录
-
- 引言
- 一、顺序表的概念
-
- 1. 线性表
- 二、 顺序表的基本形式
-
- 例子
- 三、顺序表的结构和实现
-
- 1.顺序表的基本结构
- 2.顺序表的两种基本实现方式
-
- 例子
- 3.元素存储区的扩充
- 4.元素存储区的替换
- 四、顺序表的操作
-
- 1.增加元素
- 2.删除元素
- 五、利用python自定义顺序表(数组)
-
- 1.动态数组
- 2. 动态数组时间复杂度分析
- 3.动态数组的均摊复杂度
- 4.复杂度震荡
- 六、python中的顺序表
-
- 1.list的基本技术实现
-
- 1.1 列表操作时间复杂度
- 2.字典时间复杂度
引言
数组与顺序表概念相同,顺序表,顾名思义,即将元素顺序地存放在连续存储区里,元素之间的顺序关系由存储关系来表示。
一、顺序表的概念
1. 线性表
线性表:将这样一组元素看成一个序列,用元素在序列里的位置和顺序,表示数据之间的某种关系。根据线性表的实际存储方式,分为两种实现模型:
- 顺序表,将元素顺序地存放在一块连续的存储区里,元素间的顺序关系由它们的存储顺序自然表示。
顺序表最大的优点是顺序查询
顺序表(数组)最好应用于索引“有语义”的情况,但并不是所有有语义的索引都适用,如身份证(空间太大了) - 链表,将元素存放在通过链接构造起来的一系列存储块中。
二、 顺序表的基本形式
如果每个元素大小相同,则使用顺序表的基本布局。如果每个元素大小不统一,则必须使用元素外置的顺序表,将实际元素另行存储

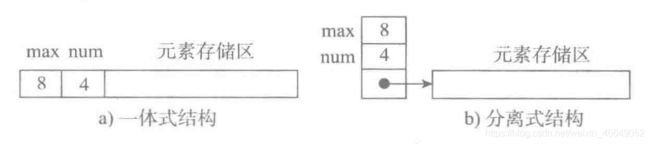
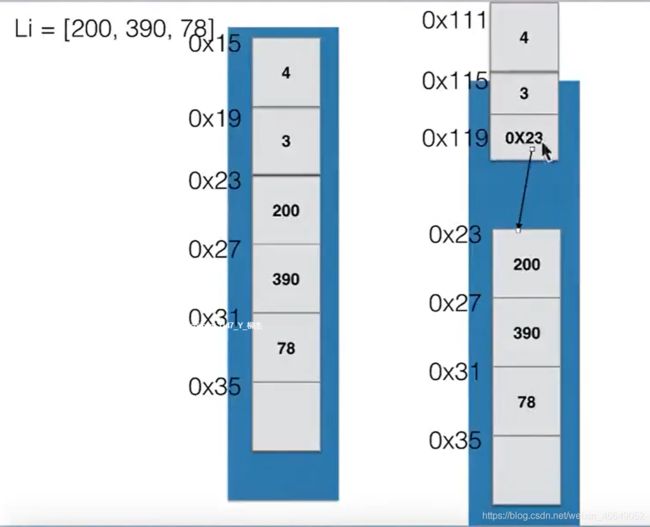
图 a a a是顺序表的基本形式,数据元素本身连续存储,每个元素所占的存储单元大小固定相同,元素的下标是其逻辑地址,而元素存储的物理地址(实际内存地址)可以通过存储区的起始地址 L o c ( e 0 ) Loc (e_0) Loc(e0)加上逻辑地址(第 i i i个元素)与存储单元大小( c c c)的乘积计算而得,即: L o c ( e i ) = L o c ( e 0 ) + c ∗ i Loc(e_i) = Loc(e_0) + c*i Loc(ei)=Loc(e0)+c∗i
图b是元素外置的顺序表,如果元素的大小不统一,则须采用图b的元素外置的形式,将实际数据元素另行存储,而顺序表中各单元位置保存对应元素的地址信息(即链接)。由于每个链接所需的存储量相同,通过上述公式,可以计算出元素链接的存储位置,而后顺着链接找到实际存储的数据元素。
图b中的c不再是数据元素的大小,而是存储一个链接地址所需的存储量,这个量通常很小。
图b这样的顺序表也被称为对实际数据的索引,这是最简单的索引结构。
例子
三、顺序表的结构和实现
1.顺序表的基本结构
一个顺序表的完整信息包括两部分,分为数据和表头信息,一部分是表中的元素集合,另一部分是为实现正确操作而需记录的信息,即有关表的整体情况的信息,这部分信息主要包括元素存储区的容量和当前表中已有的元素个数两项。
2.顺序表的两种基本实现方式
图a为一体式结构,存储表信息的单元与元素存储区以连续的方式安排在一块存储区里,两部分数据的整体形成一个完整的顺序表对象。
一体式结构整体性强,易于管理。但是由于数据元素存储区域是表对象的一部分,顺序表创建后,元素存储区就固定了。
图b为分离式结构,表对象里只保存与整个表有关的信息(即容量和元素个数),实际数据元素存放在另一个独立的元素存储区里,通过链接与基本表对象关联。
例子
3.元素存储区的扩充
采用分离式结构的顺序表,若将数据区更换为存储空间更大的区域,则可以在不改变表对象的前提下对其数据存储区进行了扩充,所有使用这个表的地方都不必修改。只要程序的运行环境(计算机系统)还有空闲存储,这种表结构就不会因为满了而导致操作无法进行。这种技术实现的顺序表称为动态顺序表,因为其容量可以在使用中动态变化。下面介绍两种扩充策略:
- 每次扩充增加固定数目的存储位置,如每次扩充增加10个元素位置,这种策略可称为线性增长。
特点:节省空间,但是扩充操作频繁,操作次数多。 - 每次扩充容量加倍,如每次扩充增加一倍存储空间。
特点:减少了扩充操作的执行次数,但可能会浪费空间资源。以空间换时间,推荐的方式。
4.元素存储区的替换
一体式结构由于顺序表信息区与数据区连续存储在一起,所以若想更换数据区,则只能整体搬迁,即整个顺序表对象(指存储顺序表的结构信息的区域)改变了。
分离式结构若想更换数据区,只需将表信息区中的数据区链接地址更新即可,而该顺序表对象不变。
举例:
一体式结构的表头起始位置改变了,而分离式结构的表头起始位置没有改变

四、顺序表的操作
增删改查
1.增加元素
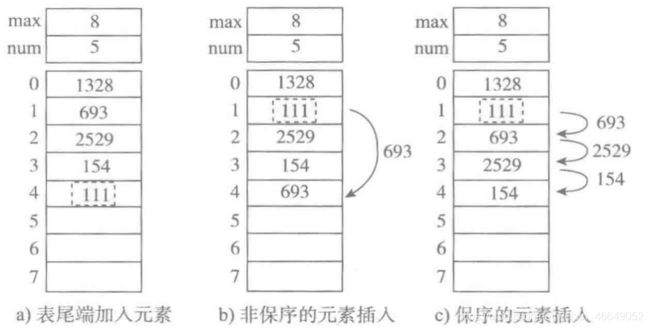
a. 尾端加入元素,时间复杂度为O(1)
b. 非保序的加入元素(不常见),时间复杂度为O(1)
c. 保序的元素加入,时间复杂度为O(n)—最坏时间复杂度
2.删除元素

a. 删除表尾元素,时间复杂度为O(1)
b. 非保序的元素删除(不常见),时间复杂度为O(1)
c. 保序的元素删除,时间复杂度为O(n)—最坏时间复杂度
五、利用python自定义顺序表(数组)
1.动态数组
静态数组的容量是有限的。但是,我们很难事先预估数组内要存储多少元素。在这种情况下,静态数组容易造成空间浪费或者空间不足。如果数组容量能够根据存储元素的多少进行伸缩,就可以很好的解决这些问题。这种数组就是动态数组。
自定义的动态数组包含
- 添加元素
- 查询与修改元素
- 包含、搜索、删除元素
"""
顺序表的特点:占用一段连续的内存空间
1. 支持随机(索引)访问,时间复杂度为O(1)
2. 添加元素时间复杂度:O(n)
3. 删除元素时间复杂度:O(n)
下面将利用python实现动态顺序表
"""
import numpy as np
class Arr:
def __init__(self,capacity = 10):
"""
构造函数—初始化参数
:param capacity: 容量,默认为10
"""
self._capacity = capacity
self._size = 0 # 初始化数组中有效元素的个数
self._data = [None] * self._capacity # None为无效元素的标识,初始化无效元素数据
def __getitem__(self, item):
"""让Arr支持索引操作"""
return self._data[item]
def getsize(self):
"""
返回数组有效元素的数目
"""
return self._size
def getcapacity(self):
"""
返回数组的容量
"""
return self._capacity
def isEmpty(self):
"""
判断数组是否为空
"""
return self._size == 0
def add(self, index, elem):
"""
向数组中添加一个元素,注意数组占用的是一段连续的内存空间,
所以在添加元素后,需要将后面的元素都向后挪一个位置,而且要注意要先从尾部开始挪,防止元素之间的覆盖
时间复杂度:O(n)
:param index: 添加的元素所在的索引
:param elem: 所要添加的元素
"""
if index < 0 or index > self._size: # 插入的位置无效
raise Exception('Add Filed. Require 0 <= index <= self._size')
if self._size == self._capacity: # 满了
self._resize(self._capacity * 2) # 默认扩容当前容量的二倍
for i in range(self._size - 1, index - 1, -1): # 从尾部开始挪动元素,在index处腾出一个空间
# 一定要注意在步长为负数的情况下,区间是左开右闭区间,即(index, self._size - 1],
# 所以是index-1,与正常的左闭右开区间是相反的!
self._data[i + 1] = self._data[i]
self._data[index] = elem # 将该位置赋值为elem
self._size += 1 # 数组有效元素数加1
def addLast(self, elem):
"""
向数组尾部添加元素
时间复杂度:O(1)
:param elem: 所要添加的元素
"""
self.add(self._size, elem)
def addFirst(self, elem):
"""
向数组头部添加元素
时间复杂度:O(n)
:param elem: 所要添加的元素
"""
self.add(0, elem)
def get(self, index):
"""
获得索引index处的元素
时间复杂度:O(1)
:param index: 数组索引
:return: 数组索引处的值
"""
if index < 0 or index >= self._size: # 判断index的合法性
raise Exception('Get failed. Index is illegal.')
return self._data[index]
def getFirst(self):
"""
获得数组首位置元素的值
:return: 首位置元素的值
"""
return self.get(0) # 直接调用get函数,安全可靠
def getLast(self):
"""
获得数组末尾元素的值
:return: 末尾元素的值
"""
return self.get(self._size - 1) # 直接调用get函数,安全可靠
def set(self, index, elem):
"""
将索引为index的元素的值设为elem
时间复杂度:O(1)
:param index: 索引
:param elem: 新的值
"""
if index < 0 or index >= self._size: # 判断index的合法性
raise Exception('Sat failed. Index is illegal.')
self._data[index] = elem
def contains(self, elem):
"""
查看数组中是否存在元素elem
时间复杂度:O(n)
:param elem: 目标元素
:return: bool值,存在为真
"""
for i in range(self._size): # 遍历
if self._data[i] == elem:
return True # 找到了就返回True
return False # 遍历完了还没找到,就返回False
def find(self, elem):
"""
在数组中查找元素,并返回元素所在的索引(如果数组中存在多个elem,只返回最左边elem的索引)
时间复杂度:O(n)
:param elem: 目标元素
:return: 元素所在的索引,没找到则返回-1(无效值)
"""
for i in range(self._size): # 遍历数组
if self._data[i] == elem:
return i # 找到就返回索引
return -1 # 没找到返回-1
def findAll(self, elem):
"""
找到值为elem全部元素的索引
:param elem: 目标元素
:return: 一个列表,值为全部elem的索引
"""
ret_list = Arr() # 建立一个新的数组用于存储索引值
for i in range(self._size): # 遍历数组
if self._data[i] == elem:
ret_list.addLast(i) # 找到就将索引添加进ret_list
return ret_list
def remove(self, index):
"""
删除索引为index的元素。index后面的元素都要向前移动一个位置
时间复杂度:O(n)
:param index: 目标索引
:return: 位于该索引的元素的值
"""
if index < 0 or index >= self._size: # index合法性检查
raise Exception('Remove failed.Require 0 <= index < self._size')
ret = self._data[index] # 拷贝一下index处的元素,便于返回
for i in range(index + 1, self._size): # index后面的元素都向前挪一个位置
self._data[i - 1] = self._data[i]
self._size -= 1 # 维护self._size
self._data[self._size] = None # 最后一个元素的垃圾回收
# 如果当前有效元素为总容量的四分之一且还存在有效元素,则将容量缩减为原来的一半,解决了复杂度震荡问题
if self._size and self._capacity // self._size == 4:
self._resize(self._capacity // 2)
return ret
def removeFirst(self):
"""
删除数组首位置的元素
时间复杂度:O(n)
:return: 数组首位置的元素
"""
return self.remove(0) # 调用remove函数
def removeLast(self):
"""
删除数组末尾的元素
时间复杂度:O(1)
:return: 数组末尾的元素
"""
return self.remove(self._size - 1) # 调用remove函数
def removeElement(self, elem):
"""
删除数组中为elem的元素,如果数组中不存在elem,那么什么都不做。如果存在多个相同的elem,只删除最左边的那个
时间复杂度:O(n)
:param elem: 要删除的目标元素
"""
index = self.find(elem) # 尝试找到目标元素(最左边的)的索引
if index != -1: # elem在数组中就删除,否则什么都不做
self.remove(index) # 调用remove函数
def removeAllElement(self, elem):
"""
删除数组内所有值为elem的元素,这里用的迭代的方法,还可以用递归
:param elem: 要删除的目标元素
"""
while True:
index = self.find(elem) # 循环来找elem,如果还存在就继续删除
if index != -1: # 若存在
self.remove(index)
else:
break
def get_Max_index(self):
"""
获取数组中的最大元素的索引,返回最大元素的索引值,如果有多个最大值,默认返回最左边那个的索引
时间复杂度:O(n)
:return: 最大元素的索引
"""
if self.isEmpty():
raise Exception('Error, array is Empty!')
max_elem_index = 0 # 记录最大值的索引,初始化为0
for i in range(1, self.getsize()): # 从索引1开始遍历,一直到数组尾部
if self._data[i] > self._data[max_elem_index]: # 如果当前索引的值大于最大值索引处元素的值
max_elem_index = i # 更新max_elem_index,这样它还是当前最大值的索引
return max_elem_index # 遍历完后,将数组的最大值的索引返回
def removeMax(self):
"""
删除数组中的最大元素,返回最大元素的值,如果有多个最大值,默认值删除最左边那个
时间复杂度:O(n)
:return: 最大元素
"""
return self.remove(self.get_Max_index()) # 直接调用remove函数删除最大值
def get_Min_index(self):
"""
获取数组中的最小元素的索引,返回最小元素的索引值,如果有多个最小值,默认返回最左边那个的索引
时间复杂度:O(n)
:return: 最小元素的索引
"""
if self.isEmpty():
raise Exception('Error, array is Empty!')
min_elem_index = 0 # 记录最小值的索引,初始化为0
for i in range(1, self.getsize()): # 从索引1开始遍历,一直到数组尾部
if self._data[i] < self._data[min_elem_index]: # 如果当前索引的值小于最小值索引处元素的值
min_elem_index = i # 更新min_elem_index,这样它还是当前最小值的索引
return min_elem_index # 遍历完后,将数组的最小值的索引返回
def removeMin(self):
"""
删除数组中的最小元素,返回最小元素的值,如果有多个最小值,默认值删除最左边那个
时间复杂度:O(2n),可以看成是O(n)的
:return: 最小元素
"""
return self.remove(self.get_Min_index())
def swap(self, index1, index2):
"""
交换分别位于索引index1和索引index2处的元素
:param index1: 索引1
:param index2: 索引2
"""
if index1 < 0 or index2 < 0 or index1 >= self._size or index2 >= self._size: # 合法性检查
raise Exception('Index is illegal')
self._data[index1], self._data[index2] = self._data[index2], self._data[index1] # 交换元素
def printArr(self):
"""对数组元素进行打印"""
for i in range(self._size):
print(self._data[i], end=' ')
print('\nSize: %d-----Capacity: %d' % (self.getsize(), self.getcapacity()))
# private
def _resize(self, new_capacity):
"""
数组容量放缩至new_capacity,私有成员函数
:param new_capacity: 新的容量
"""
new_arr = Arr(new_capacity) # 建立一个新的数组new_arr,容量为new_capacity
for i in range(self._size):
new_arr.addLast(self._data[i]) # 将当前数组的元素按当前顺序全部移动到new_arr中
self._capacity = new_capacity # 数组容量变为new_capacity
self._data = new_arr._data # 将new_arr._data赋值给self._data,从而完成数组的容量放缩操作
if __name__ == '__main__':
# 随机数种子
np.random.seed(7)
# 实例化对象
test = Arr()
# 有效元素数目
print(test.getsize())
# 容量
print(test.getcapacity())
# 是否为空
print(test.isEmpty())
# 添加元素
for i in range(8):
test.add(0, np.random.randint(5))
# 打印数组
test.printArr()
# 往尾部添加2
test.addLast(2)
# 打印数组
test.printArr()
# 获得索引为3的元素
print(test.get(3))
# 将索引为3的元素赋值为10
test.set(3, 10)
# 打印数组
test.printArr()
# 查看数组中是否含有元素10
print(test.contains(10))
# 找到元素为4的索引
print(test.find(4))
# 找到元素为1的全部索引
test.findAll(1).printArr()
# 删除索引为3的元素
test.remove(3)
# 打印数组
test.printArr()
# 删除数组第一个位置的元素
test.removeFirst()
# 删除数组最后一个位置的元素
test.removeLast()
# 打印数组
test.printArr()
# 删除数组中元素4
test.removeElement(4)
# 打印数组
test.printArr()
# 删除数组中的所有3
test.removeAllElement(3)
# 打印数组
test.printArr()
# 在数组末尾添加元素
for i in range(30):
test.addLast(np.random.randint(10))
# 打印数组
test.printArr()
# 索引为3的元素
print(test[3])
# 交换索引0,1处的元素
test.swap(0, 1)
# 打印数组
test.printArr()
0
10
True
1 0 1 4 3 3 1 4
Size: 8-----Capacity: 10
1 0 1 4 3 3 1 4 2
Size: 9-----Capacity: 10
4
1 0 1 10 3 3 1 4 2
Size: 9-----Capacity: 10
True
7
0 2 6
Size: 3-----Capacity: 10
1 0 1 3 3 1 4 2
Size: 8-----Capacity: 10
0 1 3 3 1 4
Size: 6-----Capacity: 10
0 1 3 3 1
Size: 5-----Capacity: 10
0 1 1
Size: 3-----Capacity: 10
0 1 1 8 7 6 4 0 7 0 7 6 3 5 8 8 7 5 0 0 2 8 9 6 4 9 7 3 3 8 3 0 1
Size: 33-----Capacity: 40
8
1 0 1 8 7 6 4 0 7 0 7 6 3 5 8 8 7 5 0 0 2 8 9 6 4 9 7 3 3 8 3 0 1
Size: 33-----Capacity: 40
静态数组
数组空间不够了会弹出异常,而不是进行扩容。这里以add函数为例,
def add(self, index, elem):
"""
向数组中添加一个元素,注意数组占用的是一段连续的内存空间,
所以在添加元素后,需要将后面的元素都向后挪一个位置,而且要注意要先从尾部开始挪,防止元素之间的覆盖
时间复杂度:O(n)
:param index: 添加的元素所在的索引
:param elem: 所要添加的元素
"""
if index < 0 or index > self._size: # 插入的位置无效
raise Exception('Add Filed. Require 0 <= index <= self._size')
if self._size == self._capacity: # 满了
raise Exception('illegal argumnet. failed array is already full')
# self._resize(self._capacity * 2) # 默认扩容当前容量的二倍
for i in range(self._size - 1, index - 1, -1): # 从尾部开始挪动元素,在index处腾出一个空间
# 一定要注意在步长为负数的情况下,区间是左开右闭区间,即(index, self._size - 1],
# 所以是index-1,与正常的左闭右开区间是相反的!
self._data[i + 1] = self._data[i]
self._data[index] = elem # 将该位置赋值为elem
self._size += 1 # 数组有效元素数加1
2. 动态数组时间复杂度分析
- 增、删—O(n)
- 改—已知索引O(1),未知索引O(n)
- 查—已知索引O(1),未知索引O(n)
3.动态数组的均摊复杂度
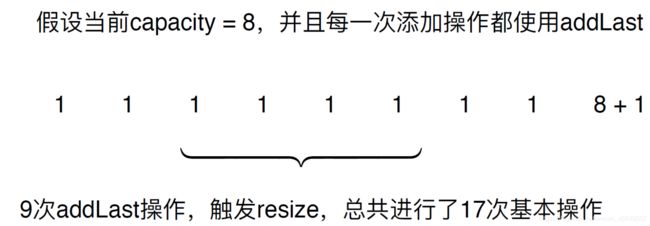
假设capacity=m,m+1次addlast,触发resize,总共进行2m+1次基本操作平均,每次addlast,进行2次基本操作。故,resize操作的均摊复杂度为O(1)
4.复杂度震荡
def remove(self, index):
"""
删除索引为index的元素。index后面的元素都要向前移动一个位置
时间复杂度:O(n)
:param index: 目标索引
:return: 位于该索引的元素的值
"""
if index < 0 or index >= self._size: # index合法性检查
raise Exception('Remove failed.Require 0 <= index < self._size')
ret = self._data[index] # 拷贝一下index处的元素,便于返回
for i in range(index + 1, self._size): # index后面的元素都向前挪一个位置
self._data[i - 1] = self._data[i]
self._size -= 1 # 维护self._size
self._data[self._size] = None # 最后一个元素的垃圾回收
# 如果当前有效元素为总容量的四分之一且还存在有效元素,则将容量缩减为原来的一半,解决了复杂度震荡问题
if self._size and self._capacity // self._size == 4:
self._resize(self._capacity // 2)
return ret
如果这一句改为
if self._size and self._capacity // self._size == 2:
就会发生复杂度震荡问题。即当一个数组满了,在尾部再添加一个元素,就需要扩容。即此时addLast的时间复杂度为O(n)。然后在从尾部删除一个元素,就需要缩容。即此时removeLast的时间复杂度为O(n)。
六、python中的顺序表
Python中的list和tuple两种类型采用了顺序表的实现技术。
tuple是不可变类型,即不变的顺序表,因此不支持改变其内部状态的任何操作,而其他方面,则与list的性质类似。
1.list的基本技术实现
Python标准类型list就是一种元素个数可变的线性表,可以加入和删除元素,并在各种操作中维持已有元素的顺序(即保序)。
行为特征:
1.基于下标(位置)的高效元素访问和更新,时间复杂度应该是O(1);
为满足该特征,应该采用顺序表技术,表中元素保存在一块连续的存储区中。
2.允许任意加入元素,而且在不断加入元素的过程中,表对象的标识(函数id得到的值)不变。为满足该特征,就必须能更换元素存储区,并且为保证更换存储区时list对象的标识id不变,只能采用分离式实现技术。
list就是一种采用分离式技术实现的动态顺序表
在Python的官方实现中,list实现采用了如下的策略:在建立空表(或者很小的表)时,系统分配一块能容纳8个元素的存储区;在执行插入操作(insert或append)时,如果元素存储区满就换一块4倍大的存储区。但如果此时的表已经很大(目前的阀值为50000),则改变策略,采用加一倍的方法。引入这种改变策略的方式,是为了避免出现过多空闲的存储位置。
1.1 列表操作时间复杂度
2.字典时间复杂度
如果对您有帮助,麻烦点赞关注,这真的对我很重要!!!如果需要互关,请评论或者私信!
![]()