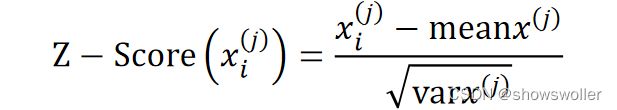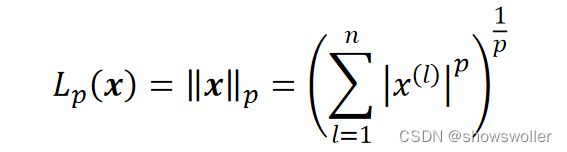【Python机器学习】特征工程含义、方法、对应函数详解(图文解释)
觉得有帮助请点赞关注收藏~~~
特征工程
特征工程的目标是从实例的原始数据中提取出供模型训练的合适特征。在掌握了机器学习的算法之后,特征工程就是最具创造性的活动了。 特征的提取与问题的领域知识密切相关
一般来说,进行特征工程,要先从总体上理解数据,必要时可通过可视化来帮助理解,然后运用领域知识进行分析和联想,处理数据提取出特征。并不是所有提取出来的特征都会对模型预测有正面帮助,还需要通过预测结果来对比分析。
进行特征工程,通常要用到numpy、pandas、sklearn、matplotlib等扩展库。
数据总体分析
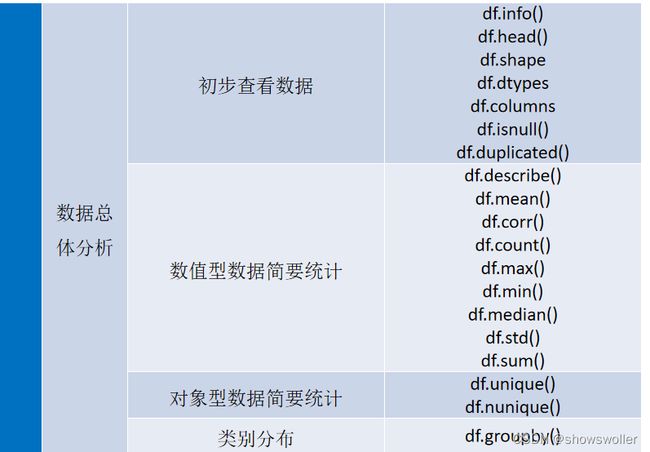
得到样本数据后,先要对数据的总体概况进行初步分析。分析数据的总体概况,一般是根据经验进行,没有严格的步骤和程序,内容主要包括查看数据以及数据的维度、属性和类型,对数据进行简要统计,分析数据类别分布等。
对于数值型的特征,数据统计常从平均值、最小值、最大值、标准差、较小值、中值、较大值等等指标入手。对于对象型的类别特征,数据统计常从唯一值个数、众数及其次数等指标入手。
部分对应函数如下
数据预处理
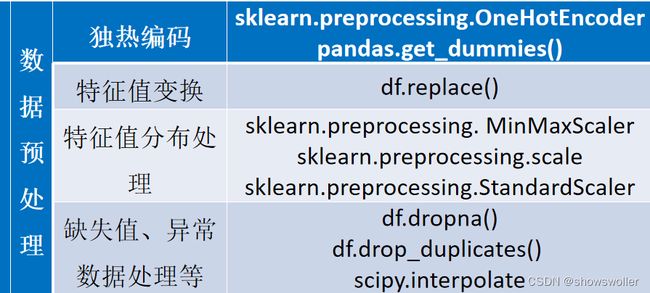
1.独热编码
对独热编码的处理,sklearn在preprocessing包中提供了OneHotEncoder类。深度学习框架也提供了类似处理方法。
2.特征值变换
为了适合算法需要,有时需要对特征值进行某种变换。常用的变换包括平方、开方、取对数和差分运算等,即:
3.特征值分布处理
有些算法对特征的取值分布比较敏感,需要预先对取值的分布进行调整。
如样本的第j个特征x^(j)的均值估计为meanx^(j)=1/m∑_i=1^m▒x_i^(j),方差估计为varx^(j)=1/m∑_i=1^m▒(x_i^(j)−meanx^(j))^2,则x_i^(j)的标准化操作为:
实现标准化操作的有sklearn.preprocessing包的scale()函数和StandardScaler类。
正则化(Normalization)是对样本进行的操作,它先计算每个样本的所有特征值的p范数,然后将该样本中的每个特征除以该范数,其结果是使得每个样本的特征值组成的向量的p范数等于1。范数的计算:
实现正则化操作的有sklearn.preprocessing包的normalize()函数和Normalizer()类。
4.缺失数据处理
有的算法能够自己处理缺失值。
当使用不能处理缺失值的算法时,或者是想自已处理缺失值时,有以下两种方法。一是删除含有缺失的样本或者特征,这种方法会造成信息损失,可能会训练出不合理的模型。二是补全缺失值,这是常用的方法,即用某些值来代替缺失值。补全缺失值的目的是想最大限度地利用数据,以提高预测成功率。
对于补全缺失值,有两种做法。
一种方法是将所有的缺失值都分为一类,相当于将缺失值的这些样本作为一个子集来训练。
另一种方法是所谓的插补(imputation),即用最可能的值来代替缺失值。插补的做法,实际上也是预测,也就是说,是采用机器学习的方法来补全机器学习所需要的样本。
常用的插补方法有:1)均值、众数插补,对于连续型特征,可采用均值来插补缺失数据,对于离散性的特征,可采用众数来插补缺失数据。2)建模预测,利用其它特征值来建模预测缺失的特征值,它的做法与机器学习的方法完全一样,将缺失特征作为待预测的标签,将未缺失的样本划分训练集和验证集并训练模型。3)插值,利用本特征的其它值来建模预测缺失值,常用的方法是拉格朗日插值法和牛顿插值法
在scipy.interpolate模块中提供了插值函数。
异常数据是明显偏离其余值的特征值。异常数据也称为离群点。通过统计分析可以发现离群点。统计分析中,常采用所谓的3σ原则来筛选离群点。3σ原则是正态分布中,与均值超过3倍标准差的值。在正态分布的假设下,距离平均值3σ之外的值出现的概率要小于0.003,属于极个别的小概率事件。
如果是合理的异常值,则不需要处理,可以直接进行训练。如果是不合理的异常值,可删除该值,并按缺失值的处理方法进行处理。
特征选择
1.根据特征取值的变化
如果某个特征取值的方差很小,也就是说该特征的值变化很小,那么可以认为它对标签值的影响很小,因此,必要时可以抛弃该特征。以极端的情况来举例,如果某特征取值的方差为0,那么说明所有样本的该特征的值都相同,显然,该特征对模型建立没有贡献。
2.根据特征与标签的相关性
可将所有样本的某特征的取值看成一个向量。同样也可将所有样本的标签值看成一个向量。因此,可以用向量的相关性指标(协方差、相关系数、相关距离等)来度量特征取值与标签值的相关程度。
条件概率也是体现相关性的指标。通过比较标签取值的概率值以及在某特征条件下标签取值的概率值,可以知道标签与该特征是否独立。
与标签相关性弱的特征可以在必要时不采用。
3.根据不同特征之间的相关性
如果两个特征有强烈的相关性,那么会出现两列系数不固定的情况,即在稳定标签值的情况下,其中一列的系数的升高可以通过另一列系数的降低来弥补,因此会出现差异较大的模型,也称为模型的方差较大。
特征强相关时,应该去掉其中多余的特征。
4.用模型尝试去特征
每次用去掉一个特征剩下的数据去训练模型,可以比较出哪个特征对模型的影响最小,并将其去掉。
5.根据某些算法对特征的打分
有的算法可以分析出特征的重要程度,如决策树和随机森林算法。根据分析结论选择特征即可。
创作不易 觉得有帮助请点赞关注收藏~~~