动手学习深度学习（总结梳理）——11. 基础卷积神经网络

目录

1. 从全连接层到卷积

2. 图像卷积

2.1 互相关运算

2.2 卷积层

2.3 图像中的目标边缘检测

2.4 学习卷积核

3. 填充和步幅

3.1 填充

3.2 步幅

4. 多输入多输出通道 

 4.1 多输入通道

4.2 多输出通道

4.3 1 x 1卷积层

5 池化层

5.1 最大池化层和平均池化层

5.2 填充和步幅

5.3 多个通道

6 QA环节

6.1 卷积核的大小体现了局部性的特征，那么什么体现了平移不变性？

6.2 这几个超参数的影响的重要程度排序是怎么样的？核大小，填充，步幅？

6.3 现在已经有很多经典的网络结构了，对应于各种任务有各种结构，我们平时自己去设计卷积核大小和网络结构的情况多吗？

6.4 如果通过多层卷积，最后输出和输入形状相同，特征会丢失吗？

6.5 多层卷积算出来的是不是可以理解成图像的多种不同的纹理？

6.6 计算卷积的时候，bias的有无对结果影响大吗？bias的作用怎么去解释？

6.7 池化层一般放在什么位置？

---

1. 从全连接层到卷积

从多重感知机的局限性——》 平移不变性和局部性 ——》通道

2. 图像卷积

2.1 互相关运算

严格来说，卷积层是个错误的叫法，因为它所表达的运算其实是互相关运算（cross-correlation），而不是卷积运算。在卷积层中，输入张量和核张量通过互相关运算产生输出张量。

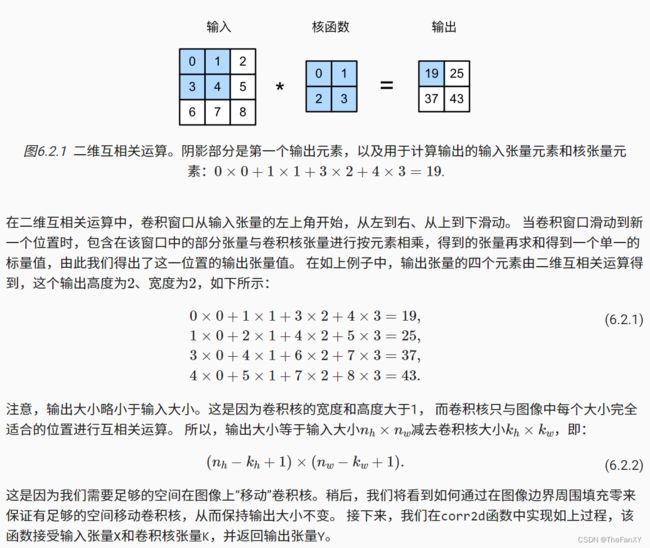
首先，我们暂时忽略通道（第三维）这一情况，看看如何处理二维图像数据和隐藏表示。在下图中，输入是高度为3、宽度为3的二维张量（即形状为3×3）。卷积核的高度和宽度都是2，而卷积核窗口（或卷积窗口）的形状由内核的高度和宽度决定（即2×2）。

​

 手动模拟以上的卷积互相关运算的过程

import torch
from torch import nn
from d2l import torch as d2l

def corr2d(X, K):
    '''计算二维互相关运算'''
    h, w = K.shape
    Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i, j] = (X[i: i + h, j:j + w] * K).sum()
    return Y

X = torch.tensor([[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]])
K = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
corr2d(X, K)        '''
tensor([[19., 25.],
        [37., 43.]])        '''

2.2 卷积层

基于上面定义的corr2d函数实现二维卷积层。在__init__构造函数中，将weight和bias声明为两个模型参数。前向传播函数调用corr2d函数并添加偏置。高度和宽度分别为h和w的卷积核可以被称为h×w卷积或h×w卷积核。 我们也将带有h×w卷积核的卷积层称为h×w卷积层。

class Conv2D(nn.Module):
    def __init__(self, kernel_size):
        super().__init__()
        self.weight = nn.Parameter(torch.rand(kernel_size))
        self.bias = nn.Parameter(torch.zeros(1))

    def forward(self, x):
        return corr2d(x, self.weight) + self.bias

2.3 图像中的目标边缘检测

如下是卷积层的一个简单应用：通过找到像素变化的位置，来检测图像中不同颜色的边缘。 首先，我们构造一个6×8像素的黑白图像。中间四列为黑色（0），其余像素为白色（1）

X = torch.ones((6, 8))
X[:, 2:6] = 0
X        '''
tensor([[1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.]])    '''

接下来，我们构造一个高度为1、宽度为2的卷积核K。当进行互相关运算时，如果水平相邻的两元素相同，则输出为零，否则输出为非零。

K = torch.tensor([[1.0, -1.0]])

现在，我们对参数X（输入）和K（卷积核）执行互相关运算。 如下所示，输出Y中的1代表从白色到黑色的边缘，-1代表从黑色到白色的边缘，其他情况的输出为0。

Y = corr2d(X, K)
Y                '''
tensor([[ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.]])'''

现在我们将输入的二维图像转置，再进行如上的互相关运算。 其输出如下，之前检测到的垂直边缘消失了。 不出所料，这个卷积核K只可以检测垂直边缘，无法检测水平边缘。

corr2d(X.t(), K)            '''
tensor([[0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.]])    '''

2.4 学习卷积核

如果我们只需寻找黑白边缘，那么以上[1, -1]的边缘检测器足以。然而，当有了更复杂数值的卷积核，或者连续的卷积层时，我们不可能手动设计滤波器。那么我们是否可以学习由X生成Y的卷积核呢？

现在让我们看看是否可以通过仅查看“输入-输出”对来学习由X生成Y的卷积核。 先构造一个卷积层，并将其卷积核初始化为随机张量。接下来，在每次迭代中，我们比较Y与卷积层输出的平方误差，然后计算梯度来更新卷积核。为了简单起见，我们在此使用内置的二维卷积层，并忽略偏置。

''' 构造一个二维卷积层，它具有1个输出通道和形状为（1，2）的卷积核 '''
conv2d = nn.Conv2d(1,1, kernel_size=(1, 2), bias=False)

''' 这个二维卷积层使用四维输入和输出格式（批量大小、通道、高度、宽度），'''
''' 其中批量大小和通道数都为1 '''
X = X.reshape((1, 1, 6, 8))
Y = Y.reshape((1, 1, 6, 7))
lr = 3e-2  ''' 学习率 '''

for i in range(10):
    Y_hat = conv2d(X)
    l = (Y_hat - Y) ** 2
    conv2d.zero_grad()
    l.sum().backward()
    ''' 迭代卷积核 '''
    conv2d.weight.data[:] -= lr * conv2d.weight.grad
    if (i + 1) % 2 == 0:
        print(f'epoch {i+1}, loss {l.sum():.3f}')

在10次迭代之后，误差已经降到足够低。现在我们来看看我们所学的卷积核的权重张量。你会发现它很接近我们之前所声明的权重张量。

conv2d.weight.data.reshape((1, 2))    '''
tensor([[ 0.9990, -0.9791]])    '''

3. 填充和步幅

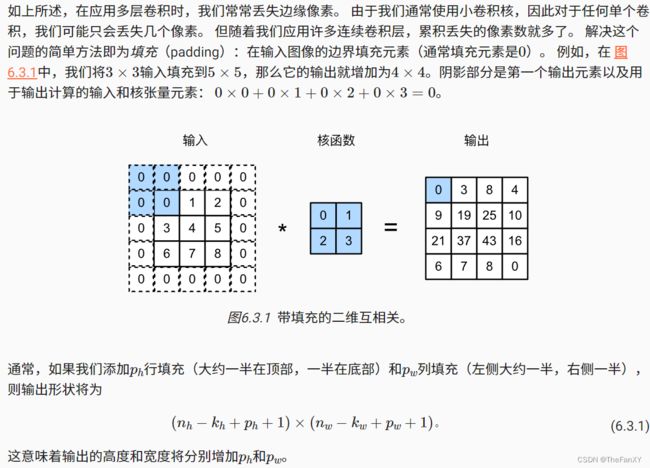
假设以下情景： 有时，在应用了连续的卷积之后，我们最终得到的输出远小于输入大小。这是由于卷积核的宽度和高度通常大于1所导致的。比如，一个240×240像素的图像，经过10层5×5的卷积后，将减少到200×200像素。如此一来，原始图像的边界丢失了许多有用信息。而填充是解决此问题最有效的方法。 有时，我们可能希望大幅降低图像的宽度和高度。例如，如果我们发现原始的输入分辨率十分冗余。步幅则可以在这类情况下提供帮助。

3.1 填充

​

import torch
from torch import nn


''' 为了方便起见，我们定义了一个计算卷积层的函数。'''
''' 此函数初始化卷积层权重，并对输入和输出提高和缩减相应的维数'''
def comp_conv2d(conv2d, X):
    ''' 这里的（1，1）表示批量大小和通道数都是1 '''
    X = X.reshape((1, 1) + X.shape)
    Y = conv2d(X)
    ''' 省略前两个维度：批量大小和通道 '''
    return Y.reshape(Y.shape[2:])

''' 请注意，这里每边都填充了1行或1列，因此总共添加了2行或2列 '''
conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1)
X = torch.rand(size=(8, 8))
comp_conv2d(conv2d, X).shape    '''
torch.Size([8, 8])        '''

当卷积核的高度和宽度不同时，我们可以填充不同的高度和宽度，使输出和输入具有相同的高度和宽度。如下我们使用高度为5，宽度为3的卷积核，高度和宽度两边的填充分别为2和1。

conv2d = nn.Conv2d(1, 1, kernel_size=(5, 3), padding=(2, 1))
comp_conv2d(conv2d, X).shape    '''
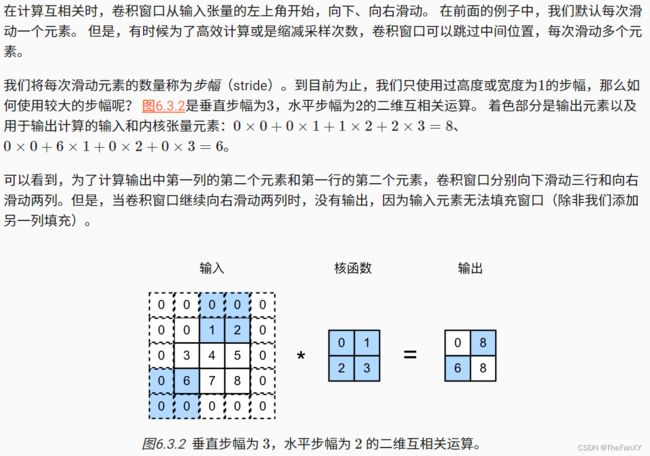
torch.Size([8, 8])    '''

3.2 步幅

conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1, stride=2)
comp_conv2d(conv2d, X).shape    '''
torch.Size([4, 4])        '''

 接下来，看一个稍微复杂的例子。

conv2d = nn.Conv2d(1, 1, kernel_size=(3, 5), padding=(0, 1), stride=(3, 4))
comp_conv2d(conv2d, X).shape    '''
torch.Size([2, 2])        '''

4. 多输入多输出通道 

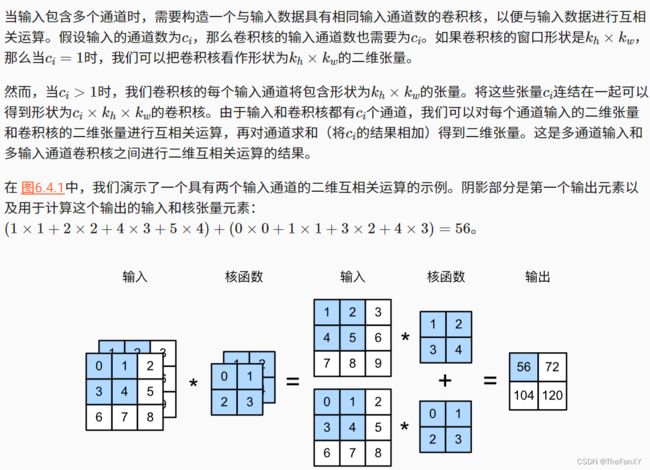
 4.1 多输入通道

import torch
from d2l import torch as d2l

def corr2d_multi_in(X, K):
    ''' 先遍历“X”和“K”的第0个维度（通道维度），再把它们加在一起    '''
    return sum(d2l.corr2d(x, k) for x, k in zip(X, K))

X = torch.tensor([[[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]],
               [[1.0, 2.0, 3.0], [4.0, 5.0, 6.0], [7.0, 8.0, 9.0]]])
K = torch.tensor([[[0.0, 1.0], [2.0, 3.0]], [[1.0, 2.0], [3.0, 4.0]]])

corr2d_multi_in(X, K)        '''
tensor([[ 56.,  72.],
        [104., 120.]])       '''

4.2 多输出通道

 torch.stack（）扩张维度的拼接函数

def corr2d_multi_in_out(X, K):
    ''' 迭代“K”的第0个维度，每次都对输入“X”执行互相关运算 '''
    ''' 最后将所有结果都叠加在一起 '''
    return torch.stack([corr2d_multi_in(X, k) for k in K], 0)

将核张量K与K+1（K中每个元素加1）和K+2连接起来，构造了一个具有3个输出通道的卷积核。

K = torch.stack((K, K + 1, K + 2), 0)
K.shape        '''
torch.Size([3, 2, 2, 2])    '''

下面，我们对输入张量X与卷积核张量K执行互相关运算。现在的输出包含3个通道，第一个通道的结果与先前输入张量X和多输入单输出通道的结果一致。

corr2d_multi_in_out(X, K)    '''
tensor([[[ 56.,  72.],
         [104., 120.]],

        [[ 76., 100.],
         [148., 172.]],

        [[ 96., 128.],
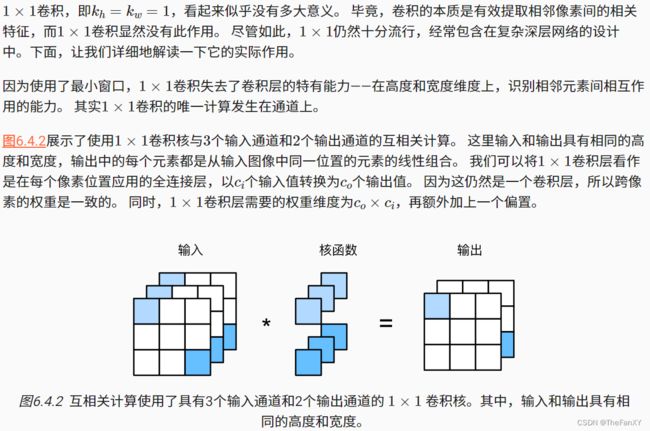
         [192., 224.]]])     '''

4.3 1 x 1卷积层

def corr2d_multi_in_out_1x1(X, K):
    c_i, h, w = X.shape
    c_o = K.shape[0]
    X = X.reshape((c_i, h * w))
    K = K.reshape((c_o, c_i))
    ''' 全连接层中的矩阵乘法 '''
    Y = torch.matmul(K, X)
    return Y.reshape((c_o, h, w))

当执行1×1卷积运算时，上述函数相当于先前实现的互相关函数corr2d_multi_in_out。让我们用一些样本数据来验证这一点。

X = torch.normal(0, 1, (3, 3, 3))
K = torch.normal(0, 1, (2, 3, 1, 1))

Y1 = corr2d_multi_in_out_1x1(X, K)
Y2 = corr2d_multi_in_out(X, K)
assert float(torch.abs(Y1 - Y2).sum()) < 1e-6

5 池化层

5.1 最大池化层和平均池化层

具有双重目的：降低卷积层对位置的敏感性，同时降低对空间降采样表示的敏感性。在下面的代码中的pool2d函数，我们实现汇聚层的前向传播。 

import torch
from torch import nn
from d2l import torch as d2l

def pool2d(X, pool_size, mode='max'):
    p_h, p_w = pool_size
    Y = torch.zeros((X.shape[0] - p_h + 1, X.shape[1] - p_w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            if mode == 'max':
                Y[i, j] = X[i: i + p_h, j: j + p_w].max()
            elif mode == 'avg':
                Y[i, j] = X[i: i + p_h, j: j + p_w].mean()
    return Y

 简单实践一下康康效果.

X = torch.tensor([[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]])
pool2d(X, (2, 2))        '''
tensor([[4., 5.],
        [7., 8.]])       '''

pool2d(X, (2, 2), 'avg')    '''
tensor([[2., 3.],
        [5., 6.]])          '''

5.2 填充和步幅

与卷积层一样，汇聚层也可以改变输出形状。和以前一样，我们可以通过填充和步幅以获得所需的输出形状。 下面，我们用深度学习框架中内置的二维最大汇聚层，来演示汇聚层中填充和步幅的使用。 我们首先构造了一个输入张量X，它有四个维度，其中样本数和通道数都是1。

X = torch.arange(16, dtype=torch.float32).reshape((1, 1, 4, 4))
X            '''
tensor([[[[ 0.,  1.,  2.,  3.],
          [ 4.,  5.,  6.,  7.],
          [ 8.,  9., 10., 11.],
          [12., 13., 14., 15.]]]])    '''

默认情况下，深度学习框架中的步幅与汇聚窗口的大小相同。 因此，如果我们使用形状为(3, 3)的汇聚窗口，那么默认情况下，我们得到的步幅形状为(3, 3)

pool2d = nn.MaxPool2d(3)
pool2d(X)    '''
tensor([[[[10.]]]])    '''

填充和步幅可以手动设定。

pool2d = nn.MaxPool2d(3, padding=1, stride=2)
pool2d(X)    '''
tensor([[[[ 5.,  7.],
          [13., 15.]]]])    '''

当然，我们可以设定一个任意大小的矩形汇聚窗口，并分别设定填充和步幅的高度和宽度。

pool2d = nn.MaxPool2d((2, 3), stride=(2, 3), padding=(0, 1))
pool2d(X)            '''
tensor([[[[ 5.,  7.],
          [13., 15.]]]])    '''

5.3 多个通道

在处理多通道输入数据时，池化在每个输入通道上单独运算，而不是像卷积层一样在通道上对输入进行汇总。 这意味着池化层的输出通道数与输入通道数相同。 下面，我们将在通道维度上连结张量X和X + 1，以构建具有2个通道的输入。

X = torch.cat((X, X + 1), 1)
X            '''
tensor([[[[ 0.,  1.,  2.,  3.],
          [ 4.,  5.,  6.,  7.],
          [ 8.,  9., 10., 11.],
          [12., 13., 14., 15.]],

         [[ 1.,  2.,  3.,  4.],
          [ 5.,  6.,  7.,  8.],
          [ 9., 10., 11., 12.],
          [13., 14., 15., 16.]]]])    '''

''' 如下所示，汇聚后输出通道的数量仍然是2    '''

pool2d = nn.MaxPool2d(3, padding=1, stride=2)
pool2d(X)    '''

tensor([[[[ 5.,  7.],
          [13., 15.]],

         [[ 6.,  8.],
          [14., 16.]]]])    '''

6 QA环节

6.1 卷积核的大小体现了局部性的特征，那么什么体现了平移不变性？

平移不变性是指我们不管扫描哪个区域用的都是同一个卷积核，所以采集图片信息不会因为平移而改变收集信息的策略。

6.2 这几个超参数的影响的重要程度排序是怎么样的？核大小，填充，步幅？

填充通常取核减1，会使得输入输出保持同样的大小。填充一般默认。通常步幅为1更好，当计算量太大的时候，可能就会扩大步幅，可能取2。

6.3 现在已经有很多经典的网络结构了，对应于各种任务有各种结构，我们平时自己去设计卷积核大小和网络结构的情况多吗？

虽说很鼓励自己去设计，但是事实上大多数情况下我们都会使用经典的已经打磨的很好的架构，除非你的输入是个特别奇怪的情况，比如高度低，长度特别特别长，可能经典的模型就失效了。

6.4 如果通过多层卷积，最后输出和输入形状相同，特征会丢失吗？

从信息论的角度去想，信息它一定会消失的，机器学习从本质上讲就是一个压缩的过程。把一个图片的若干信息压缩成有限个类别，它一定会丢失很多信息，但是我们需要的是通过提取有效的信息，去帮助我们完成分类或者回归的任务。

6.5 多层卷积算出来的是不是可以理解成图像的多种不同的纹理？

确实可以这么去理解，采用多种不同的卷积核，去提取图像不同的特征。

6.6 计算卷积的时候，bias的有无对结果影响大吗？bias的作用怎么去解释？

bias确实是有用的，虽然目前来看它的作用越变越小。从统计学看，当数据不均匀的时候，偏移可能是调整均匀的作用。

6.7 池化层一般放在什么位置？

一般是为了使得通过卷积层的数据输出不那么对位置敏感，所以一般放在卷积层后面。