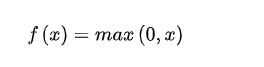卷积神经网络基础知识总结
一般来说CNN具有卷积层,池化层和完全连接层FC(正如在常规神经网络中所见),在池化层之前一般会有个激活函数。
CNN
局部连接:每个神经元不再和上一层的所有神经元相连,而只和一小部分神经元相连。这样就减少了很多参数
权值共享:一组连接可以共享同一个权重,而不是每个连接有一个不同的权重,这样又减少了很多参数。(用通俗的话说,一张特征图,是由同一个卷积核扫描一张原图得到的,共享体现在原图每个小的感知野共享同一个卷积核)
卷积层的作用
卷积是一种局部操作,**通过一定大小的卷积核作用于图像信息的局部区域获得图像的局部信息。
卷积网络中的卷积核参数是通过网络训练学出的
总结输出大小
输入体积大小H_1W_1D_1H1∗W1∗D1
四个超参数:
Filter数量KK
Filter大小FF
步长SS
零填充大小PP(如果我们的步长移动与filter的大小不适合,导致不能正好移动到边缘怎么办?用零填充)
输出体积大小H_2W_2D_2H2∗W2∗D2
H_2 = (H_1 - F + 2P)/S + 1 H2=(H1−F+2P)/S+1
W_2 = (W_1 - F + 2P)/S + 1 W2=(W1−F+2P)/S+1
D_2 = KD2=K
池化的作用
池化层不包含可学习的参数,只需要指定池化类型,池化操作核大小,池化步长等超参数,池化有平均池化,最大池化,随机池化。
作用:其实就是降采样操作。降采样,池化结果中一个元素对应于原输入数据的一个子区域,因此池化相当于在空间范围内做了维度约检,从而使模型可以抽取更广范围的特征。同时减小下一层输入的大小,进而减小计算量和参数个数。(去掉Feature Map中不重要的样本,进一步减少参数数量。)
激活函数作用
引入激活函数的目的是为了增加整个网络的表达能力(即非线性)。否则若干现行操作层的堆叠仍然只能起到线性映射的作用,无法形成复杂的函数。
常用激活函数:
Sigmoid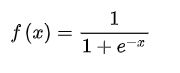
全连接层
前面的卷积和池化相当于做特征工程,提取图像的特征。后面的全连接相当于做特征加权。最后的全连接层在整个卷积神经网络中起到“分类器”的作用。
利用误差函数,如果最最后FC层的结果根据误差函数算出的误差较小,那么它是这个类别的可能性就较大,从而起到分类的作用。
首先这是卷积神经网络最后一层全连接层的构造,W是神经元的权值,K是要分类的类别数,X是上一层的输出平铺(Flatten)后的结果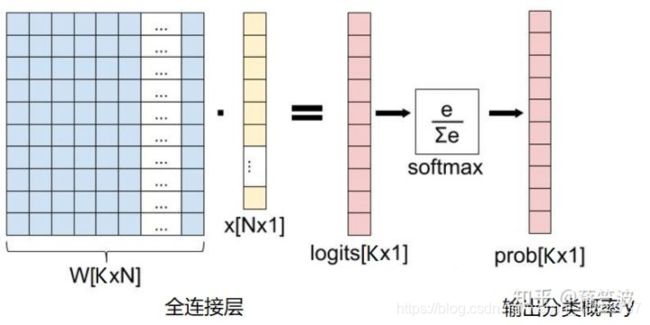
可参考https://zhuanlan.zhihu.com/p/41784404
softmax层
softmax层,这个层的主要作用就是输出物体是各个类的概率
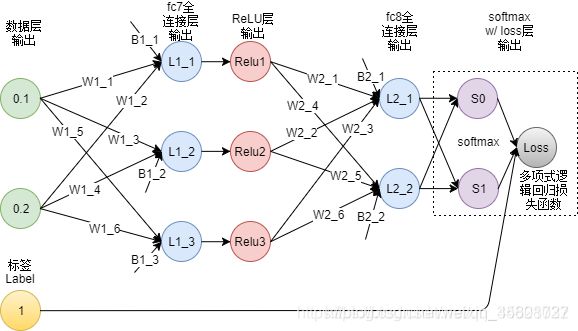
如上图所示,在全连接层得到了两个结果(有两个类别)L 2 _ 1 与L 2 _ 2 ,为了公式方便书写我们就把它们看成是y 1 和y 2 。我们想要得到的是各个类别的概率。这里需要注意在softmax层所有输出的概率之和为1。因此我们就要用到一个计算公式:
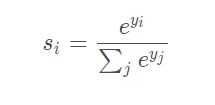
也就得到
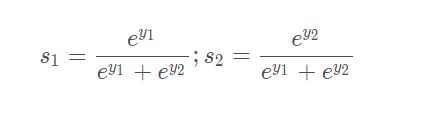
sigmoid
sigmoid输出,每个节点之间互不相干。
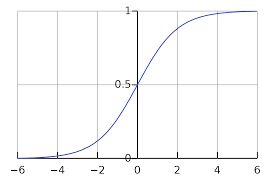
计算公式
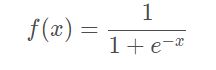
sigmoid函数主要针对二分类问题,它可以不满足概率分布。当输入一张图片让你判断是否为猫的时候,那么结果只有两种,这是满足概率分布的;如果输入一张图片,让你判断是动物还是猫,那么就不满足概率分布了。
CNN常见架构
LeNet,AlexNet,VGGNet
过拟合
如果模型的参数太多,而训练样本又太少,训练出来的模型很容易产生过拟合的现象。
型在训练数据上损失函数较小,预测准确率较高;但是在测试数据上损失函数比较大,预测准确率较低。
方法:DropOut
我们在前向传播的时候,让某个神经元的激活值以一定的概率p停止工作,这样可以使模型泛化性更强,因为它不会太依赖某些局部的特征,如图1所示。
CNN训练过程
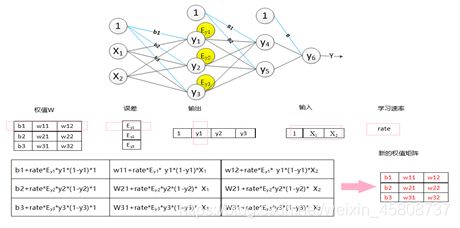
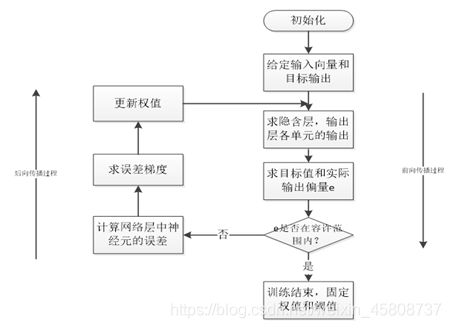
卷积神经网络的训练过程分为两个阶段。第一阶段是数据由低层次向高层次传播的阶段,即前向传播阶段。另外一个阶段是,当前向传播的出的结果与预期不符(相差较大),将误差从高层次向低层次进行传播训练的阶段,即反向传播阶段。
训练过程为:
1.网络进行权值的初始化
2.输入数据经过卷积层,池化层,FC层的前向传播得到输出值
3.求出网络的输出值 与目标值之间的误差
4.当误差大于我们的期望值时,将误差传回网络中,依次求得全连接层,池化层,卷积层的误差。各层的误差可以理解为对于网络的总误差,网络应承担多少;当误差等于或小于我们的期望值时,结束训练。
5、根据求得误差进行权值更新。然后在进入到第二步。
1.1卷积神经网络的前向传播过程
在前向传播过程中,输入的图形数据经过多层卷积层的卷积和池化处理,提出特征向量,将特征向量传入全连接层中,得出分类识别的结果。当输出的结果与我们的期望值相符时,输出结果。
1.2反向传播过程
反向传播(英语:Backpropagation,缩写为BP)是“误差反向传播”的简称,是一种与最优化方法(如梯度下降法)结合使用的,用来训练人工神经网络的常见方法。 该方法对网络中所有权重计算损失函数的梯度。 这个梯度会反馈给最优化方法,用来更新权值以最小化损失函数。(误差的反向传播)
————————————————
当卷积神经网络输出的结果与我们的期望值不相符时,则进行反向传播过程。求出结果与期望值的插值,再将误差一层一层的返回,计算出每一层的误差,然后将权值更新。该过程的主要目的是通过训练有样本和期望值来调整网络权值。
反向传播的训练过程的第一步为计算出网络的总误差:求出输出层n的输出a(n)与目标值y之间的误差,公式为:
![]()
1.2.1全连接层之间的误差传递
求出网络的总差后,进行反向传播过程,将误差传入输出层的前一层全连接层,求出在该层上,产生了多少误差。而网络的误差又是由组成该网络的神经元造成的,所以我们要求出每个神经元在网络中的误差。求上一层的误差,要找出上一层中哪些节点与该输出层连接,然后用误差乘以节点的权值,求得每个节点的误差。
1.2.2当前层为池化层,求上一层的误差
在池化层,不需要进行权值更新,只需要正确的传递所有误差到上一层。
1.2.3当前层为卷积层,求上一层的误差
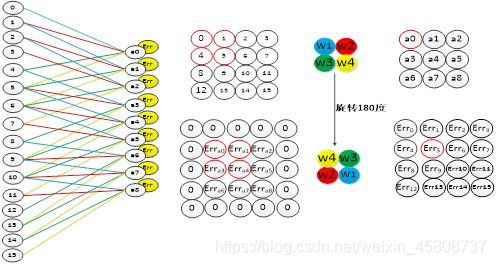
卷积层中采用的是局部连接的方式,和全连接层的误差传递方式不同,在卷积层中,误差的传递也是依靠卷积核进行传递的。在误差传递的过程,我们需要通过卷积核找到卷积层和上一层的连接节点。求卷积层的上一层的误差的过程为:先对卷积层误差进行一层全零填充,然后将卷积层进行一百八十度旋转,再用旋转后的卷积核卷积填充过程的误差矩阵,并得到了上一层的误差。如图4-7为卷积层的误差传递过程。图右上方为卷积层的向前卷积过程,而右下方为卷积层的误差传递过程。从图中可以看出,误差的卷积过程正好是沿着向前传播的过程,将误差传到了上一层。
1.3卷积神经网络权值更新
1.3.1卷积层的权值更新
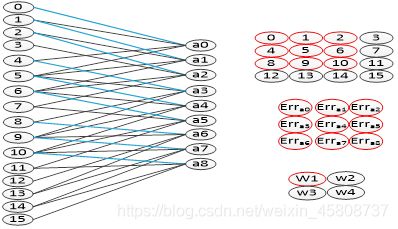
卷积层的误差更新过程为:将误差矩阵当做卷积核,卷积输入的特征图,并得到了权值的偏差矩阵,然后与原先的卷积核的权值相加,并得到了更新后的卷积核。如图4-8,图中可以看出,该卷积方式的权值连接正好和向前传播中权值的连接是一致的。
1.3.2全连接层的权值更新过程
全连接层的权值更新过程为:
1.求出权值的偏导数值
2.用节点的误差值成偏导求出权值的误差
3.原先的权值加上刚才求出的误差,得到新的权值矩阵。