【opencv】(8) 傅里叶变换,高通低通滤波器
图像处理一般分为空间域处理和频率域处理。
空间域处理是直接对图像内的像素进行处理。主要划分为灰度变换核空间滤波两种形式,灰度变换对图像内的单个像素进行处理,滤波处理涉及对图像质量的改变。
频率域处理是先将图像变换到频率域,然后在频率域对图像进行处理,最后通过反变换将图像变为空间域。
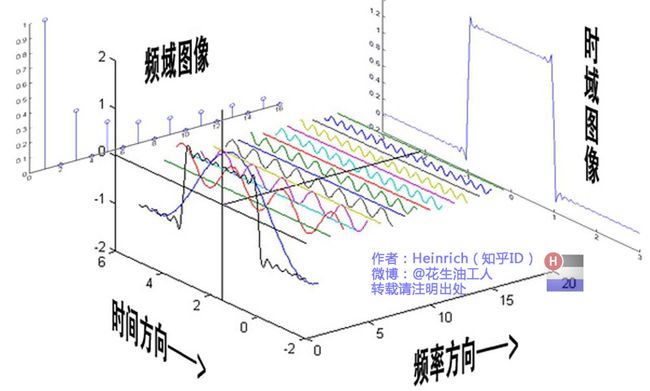
傅里叶变换可以将图像变换为频率域, 傅立叶反变换将频率域变换为空间域。
傅里叶变换的详细可看一下知乎大佬的解释:傅里叶分析之掐死教程(完整版)更新于2014.06.06 - 知乎
在图像中,高频是指变化剧烈的灰度分量,如图像的边缘轮廓区域。低频是指图像中变化缓慢的灰度分量,如图像中轮廓内的填充,非边缘区域。
傅里叶变换可进行高通滤波和低通滤波。低通滤波器:只保留低频信息。如消除图像边界,使图像变得模糊。高通滤波器:只保留高频信息,消除低频信息。如增强图像细节,描绘图像轮廓信息。
(1) 傅里叶变化函数:
cv2.dft(img, flags)
img:代表输入图像,opencv中输入图像必须转换成np.float32类型
flags:转换标识,通常为cv2.DFT_COMPLEX_OUTPUT,其他值如下:
![]()
(2) 图像频谱中的零频率分量会被移到频域图像的中心位置
np.fft.fftshift(x, axis)
x: 数组,代表输入的频谱图数据
axis: 可选,指定需要移动的轴。默认移动所有的轴
返回位移之后的数组。
使用傅里叶变换后,在得到的频谱图中,频率为0的部分会在左上角,为了计算方便,我们通常将频率为0的部分转换到频谱图中心位置。
(3) 计算二维矢量的幅值
cv2.magnitude(x, y)
x:数组类型,表示浮点型的x轴坐标,也就是实部
y:数组类型,表示浮点型的y轴坐标,也就是虚部
返回值为:x和y的平方和开根,![]()
由于cv2.dft()返回的结果是双通道的(实部和虚部),通常需要转换成图像格式[0,255],才能正常显示频谱图。公式为:
20*np.log(cv2.magnitude(x, y))
(4) 构造滤波器
傅里叶变换之后,构造一个和原图像相同size的掩模。注意:构造的掩模是三维度的,因为傅里叶变换后的结果第三维度是实部和虚部,有2个通道。掩模的shape应该和它一致。
低通滤波器:构造一个像素值全为0的掩模底板,获取频率为0的部分的中心坐标,以它为中点,设置掩模大小,掩模内的像素值都为255。把掩模覆盖到频谱图上,只保留掩模值为255的部分,其他全部删除。即在频谱图像上,只保留频率为0附近的点,其他高频点全部删除。因为掩模白色部分框住的就是所有的低频点。
高通滤波器:构造一个像素值全为255的掩模底板,获取频率为0的部分的中心坐标,以它为中点,设置掩模大小,都掩模内的像素值为0。把掩模覆盖到频谱图上,只保留掩模值为255的部分,其他全部删除。即在频谱图像上,只删除频率为0附近的点,其他高频点全部保留。因为掩模黑色部分覆盖住的就是所有的低频点。
我们在下面代码段的图中进一步理解
(5) 傅里叶逆变换函数
cv2.idft(img)
img:代表输入处理后的频谱图像
在使用cv2.dft()获得频谱图时,将低频点从边缘移动到图像中间,现在要逆变换,得把低频点还原到原始位置,使用函数: np.fft.ifftshift(处理后的频谱图) ,之后才能将频谱图转变回空间图像。
注意,逆变换后的结果是包含实部和虚部的,仍需要使用cv2.magnitude函数进行处理
1. 正向变换
import cv2
import numpy as np
import matplotlib.pyplot as plt
filepath = 'C:\\...\\opencv\\img' # 获取图片所在文件夹
#(1)正向变换
# 导入图像,变成灰度图
img = cv2.imread(filepath+'\\mh1.jpg',0)
# 转变成np.float32类型
img_float = np.float32(img)
# 傅里叶变换
dft = cv2.dft(img_float,flags=cv2.DFT_COMPLEX_OUTPUT)
# 获得频谱图,将低频值转换到中间
dft_shift = np.fft.fftshift(dft)
# 得到灰度图能表示的形式,将对实部虚部计算后的结果,映射到0-255之间
magnitude = 20*np.log(cv2.magnitude(dft_shift[:,:,0],dft_shift[:,:,1]))
# 绘图
plt.subplot(121), plt.imshow(img,cmap='gray')
plt.title('input image'), plt.xticks([]), plt.yticks([]) #不显示坐标轴
plt.subplot(122), plt.imshow(magnitude,cmap='gray')
plt.title('magnitude Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()
下图左侧是原图,右侧是FFT变换后的频谱图。右侧图中间的亮点代表的频率为0的部分,离中心点越近,频率越低,越往外发散,频率越高。
因此我们只需要把中间一小块的点抹除掉就能消除所有频率在0附近的部分,消除低频信息,实现高通滤波。或者只保留中心点附近的部分,就能消除所有的高频信息,实现高通滤波。至于怎么消除呢,我们之前提讲解过的掩模就可以用在这里。
2. 低通滤波
#(1)傅里叶正向变换
img = cv2.imread(filepath+'\\mh1.jpg',0) 导入图像,变成灰度图
# 转变成np.float32类型
img_float = np.float32(img)
# 傅里叶变换
dft = cv2.dft(img_float,flags=cv2.DFT_COMPLEX_OUTPUT)
# 获得频谱图,将低频值转换到中间
dft_shift = np.fft.fftshift(dft)
#(2)构造滤波器
# 获取频率为0部分中心点位置
rows,cols = img.shape # (471,498),分别保存图像的高和宽
crow,col = int(rows/2), int(cols/2) # 计算中心点坐标
# 构造低通滤波器,相当于构造一个掩模
mask = np.zeros((rows,cols,2),np.uint8) # 构造的size和原图相同,2通道,傅里叶变换后有实部和虚部
mask[crow-30:crow+30, col-30:col+30] = 255 # 构造一个以频率为0点中心对称,长30+30,宽30+30的一个区域,只保留区域内部的频率
#(3)滤波
# 频谱图上,低频的信息都在中间,滤波器和频谱图相乘,遮挡四周,保留中间,中间是低频
fshift = dft_shift*mask
# 在获得频谱图时,将低频点从边缘点移动到图像中间,现在要逆变换,得还回去
f_ishift = np.fft.ifftshift(fshift)
#(4)傅里叶逆变换idft
img_back = cv2.idft(f_ishift)
# 还原后的还是有实部和虚部,需要进一步处理
img_back = cv2.magnitude(img_back[:,:,0],img_back[:,:,1])
#(5)绘图
# 结果展示,低通使图像模糊
plt.subplot(121), plt.imshow(img, cmap='gray')
plt.title('input img'), plt.xticks([]), plt.yticks([]) #不显示坐标轴
plt.subplot(122), plt.imshow(img_back, cmap='gray')
plt.title('fft img'), plt.xticks([]), plt.yticks([])
plt.show()
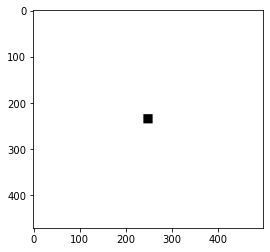
构造的滤波器是以频率等于0为中心的矩形,宽30+30,高30+30,如图1。只保留白色部分,消除黑色部分。白色部分框住的是低频信息,滤波器设置的越大,保留的低频信息也就越多,过大会保留高频信息。
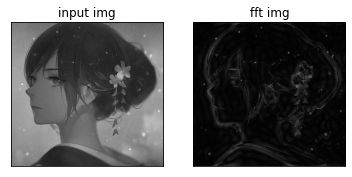
图2原图,图3是低通滤波后的图,明显变模糊了,消除了图像的边界。
3. 高通滤波
#(1)正向傅里叶变换
img = cv2.imread(filepath+'\\mh1.jpg',0) # 导入图像,变成灰度图
# 转变成np.float32类型
img_float = np.float32(img)
# 傅里叶变换
dft = cv2.dft(img_float,flags=cv2.DFT_COMPLEX_OUTPUT)
# 获得频谱图,将低频值转换到中间
dft_shift = np.fft.fftshift(dft)
#(2)构造滤波器,获取频率为0的坐标
rows,cols = img.shape #(471,498),分别保存图像的高和宽
crow,col = int(rows/2), int(cols/2) # 计算中心点坐标
# 构造高通滤波器,相当于构造一个掩模,设置的越大,低频信息删除的越多
mask = np.ones((rows,cols,2),np.uint8) # 构造的size和原图相同,2通道,傅里叶变换后有实部和虚部
mask[crow-10:crow+10, col-10:col+10] = 0 # 以频率为0处坐标为中心,宽10+10,高10+10的部分抹除
#(3)傅里叶逆变换
# 删除中间的信息,保留其他部分的信息,低频都集中在中央位置,统一删除
fshift = dft_shift*mask
# 在获得频谱图时,将低频点从边缘点移动到图像中间,现在要逆变换,得还回去
f_ishift = np.fft.ifftshift(fshift)
# 傅里叶逆变换idft
img_back = cv2.idft(f_ishift)
# 还原后的还是有实部和虚部,需要进一步处理
img_back = cv2.magnitude(img_back[:,:,0],img_back[:,:,1])
#(4)绘图
# 结果展示,只有边界信息
plt.subplot(121), plt.imshow(img, cmap='gray')
plt.title('input img'), plt.xticks([]), plt.yticks([]) #不显示坐标轴
plt.subplot(122), plt.imshow(img_back, cmap='gray')
plt.title('fft img'), plt.xticks([]), plt.yticks([])
plt.show()高通滤波器,构造一个以频率等于0为中心的矩形,宽10+10,高10+10,如图1。只保留白色部分,消除黑色部分。白色部分(像素255)框住的是高频信息,黑色部分(像素为0)设置的越大,消除的低频信息也就越多,过大会一定程度抹除一些高频信息。
图2原图,图3是高通滤波后的图,只保留了图像的边界,抹除了图像的内在信息。