DeepMind：用 GNN 学习通用推理算法

文 | 智商掉了一地

小孩子才做选择，我的模型全！都！要！

近年来，基于深度神经网络的机器学习系统取得了巨大进步，尤其是在以感知为主的任务上。这一领域表现突出的模型通常要在分布中进行泛化，意味着它们的训练和验证集代表了测试输入的预期分布。

相比之下，要真正掌握由推理主导的任务，即使是在分布外泛化 (OOD) 时，模型也需要提供合理的输出。然而大多数的神经网络在该领域的成功程度较低，虽然近年来这一领域的方法改进激增，但它们主要集中在构建专家模型上。

DeepMind 的作者们提出了一个通用的神经算法学习器——具有单一参数集的 GNN，能学习同时解决多个经典算法任务，达到相关专家模型的平均水平。

本文的主要贡献之一也是对训练、优化、输入表示和 GNN 架构进行了一系列改进，跟现有的技术相比，改进后的平均单任务性能提升了 20% 多。

论文题目:
A Generalist Neural Algorithmic Learner

论文链接:
https://arxiv.org/abs/2209.11142

---

问题探索

神经算法推理的基石是解决算法任务的能力，特别是以一种从分布中泛化的方式。

有人认为，更强大的神经推理架构可能要应用更多的算法对齐、因果和自监督学习等方法。此外，这些类型的架构可能对基于现有观察来稳健地生成新知识至关重要，特别是当这些知识脱离了训练数据领域时。

DeepMind 提出的通用算法是一个重要的里程碑，表明我们甚至可以在具有完全不同的控制流的任务中有意义地整合推理能力，并且在多个任务中，可以超过相应单任务专家的 OOD 性能（在较大任务实例上的性能）。

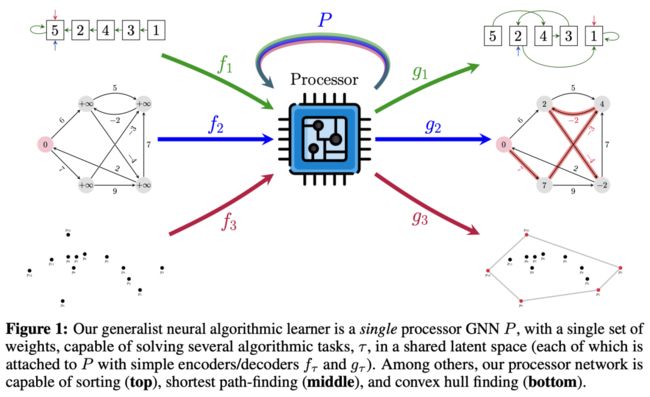▲图1 通用算法学习器

如图 1 所示，通用神经算法学习器是个具有一组权重的单处理器 GNN ，能够在一个共享的隐空间 中解决多个算法任务（每个任务都通过简单的编码器 和解码器 连接到 P 上)。其中，处理器的网络能够进行排序（顶部）、最短路径查找（中间）和凸包查找（底部）。

本文的工作属于模型的硬参数共享类，在这里的设置中，OOD 泛化意味着对更大规模问题的泛化，分布中的泛化是对相同规模问题的新实例泛化。

这里为单任务专家推理器的改进在很大程度上是由算法对齐理论推动的，这一理论的关键结果是，如果神经网络的设计组件与目标算法的操作“一致”，那么它们的样本复杂性将明显较小。遵循这一规定，对输入数据表示进行了几次更改以使这种一致性更强，修改 GNN 架构以支持高阶推理，并为双随机输出提出专用解码器。

作者指出，这个通用模型能够执行各种任务，包括排序、搜索、贪心算法、动态规划、图形算法、字符串算法和几何算法。本文实验是通过 CLRS-30 基准实现的，它是跨越上述类别的 30 个经典算法任务的集合，以及用一个统一的表示界面，使多任务模型更容易部署。实验表明，通用学习器能够有效地整合由专家模型捕获的知识。

这里将主要阐述在单任务实验上的设置与改进：

CLRS 基准中的每个算法都由许多输入、hints 和输出指定，在给定的样本中，输入和输出是固定的，而 hint 是算法中间状态的时间序列。特定任务的每个样本大小为 ，对应于 GNN 中将执行该算法的节点数。

每个算法的样本被表示为图，其中每个输入、输出和 hint 位于节点、边或图本身中，且因此具有形状 、 或 ，其中 是特征的维数，取决于它的类型。CLRS 基准定义了五种类型的特征：标量（scalar）、分类（categorical）、掩码（mask）、mask_one 和指针（pointer），它们有自己的编码解码策略和损失函数。

基础模型

本文采用与 CLRS 基准相同的编码-处理-解码模式。

编码器

在特定任务 （如插入排序）的每个时间步 中，基于任务的编码器 由每个输入和 hint 的线性编码器组成，将输入和当前 hint 编码为高维向量。这些位于节点中的输入和 hint 的 embedding 都有相同维度，它们相加在一起；在位于边和图中的 hint 和输入上也是相同情况，本文在 CLRS 的所有 30 种算法中共享这个隐空间。此外，注意在每步中，输入编码被直接送到这些 embedding ——这种召回机制显著提升了模型在长期轨迹（Long-Term Trajectories）上的鲁棒性。

处理器

embedding 被送入执行一步计算的 GNN 处理器 。处理器将输入节点、边和图 embedding 转换为已处理节点 embedding 。此外，处理器使用前一步中已处理过的节点 embedding 作为输入。有一点需要注意，相同的处理器模型可以操作任何大小的图。这里利用消息传递神经网络 MPNN，在全连接图上用最大聚合和传递消息作为基本模型，公式 1 如下。

解码器

处理后的 embedding 最终用基于任务的解码器 解码，以预测下一步的 hint 和最后一步的输出。与编码器类似，基于任务的解码器主要依赖于每个 hint 和输出的线性解码器，以及在适当的时候计算成对节点相似性的机制。具体来说，指针类解码器计算每对节点的得分 ，然后通过获取 或 （取决于使用硬预测还是软预测）来选择节点 的指针。

损失函数

hint 损失和输出损失加在一起，解码后的 hint 和输出用于在训练过程中根据其类型计算损失。对于 batch 中的每个样本， hint 预测损失按 hint 和时间进行平均，输出损失是各输出端的平均值。此外，除非在训练时使用 teacher forcing，否则每个时间步的 hint 预测结果将作为下一步的输入。

单任务改进

尤其是在学习的稳定性方面，单任务改进将在经验上很好地迁移到多任务算法学习上，这里以渐进的方式描述对模型做的所有改进，首先是数据集和训练过程中的改进：

消除 teacher forcing

在评估环节，模型无法访问数据集中的 step-by-step hint，必须依赖于自己的 hint 预测值。然而，在训练期间，有时会用 teacher forcing 来稳定轨迹（提供 ground-truth hint 值而非网络自己的预测）。

在 CLRS 基准模型中，在训练时以 0.5 的概率提供 ground-truth hint ，因为如果没有 teacher forcing，当存在标量 hint 时，损失倾向于沿着轨迹无限制地增长，从而破坏训练的稳定。在这项工作中，后续纳入了几个重要的稳定变化，这使得能够完全消除 teacher forcing，将训练与评估相一致，且避免网络在总是期望正确的 hint 预测方面过度自信。

扩充训练数据

为防止模型过度拟合固定 CLRS 训练集的统计量，这里以三种关键方式在不破坏预期大小分布偏移的情况下，增强了训练数据：

1. 首先，利用 CLRS 中的在线采样器动态生成新的训练样本，而非使用容易过拟合的固定数据集；

2. 其次，在 的混合大小示例上进行训练，这有助于模型预测不同的大小范围，而不过度拟合大小 的细节。

3. 最后，对于图算法，改变输入图的连通概率 （在许多图算法中，算法运行的步数与图的直径有关，在生成图时改变连接概率可以改变期望直径）；对于字符串匹配算法，改变要匹配的模式长度，这两者都有助于将模型暴露于不同的轨迹长度下。与原始数据集相比，这些改变大大增加了训练数据的可变性。

Soft hint 传播

当预测的 hint 在训练中作为输入反馈时，梯度可能允许也可能不允许通过它们。在以前的工作中，只有标量类 hint 允许梯度通过，因为在反馈之前，所有类别数据都通过 argmax 或阈值化从 logits 后处理为 ground-truth 格式。

相反，在这项工作中，使用 softmax 表示类别类型、mask_one 类型和指针类型，并使用 logistic sigmoid 表示掩码类型。如果没有这些 soft hint，排序算法的性能就会下降（类似于 teacher forcing 的情况），Naïve String Matcher 也是如此。

静态 hint 消除

CLRS 中的 11 个算法通过节点指针 hint 指定了节点的固定顺序，这对每个样本都是通用的，该节点指针 hint 不会沿着轨迹改变。这个 hint 预测微不足道（恒等映射，identity function），但这却给 OOD 泛化带来了一个潜在问题，因为模型可以过度拟合固定的训练值。因此，需要将此固定 hint 转化为这 11 种算法的输入，消除了显式预测它的必要性。

通过编码器初始化和梯度裁剪提高训练稳定性

原则上，标量 hint 具有无界值，并使用均方误差进行优化，因此它们的梯度可以随着预测误差的增加而快速增长。此外，预测的标量 hint 在每一步都被重新编码，这可以迅速放大整个轨迹中的误差，甚至在进行任何训练之前，就会导致信号爆炸（以及梯度）。

为纠正此问题，这里使用 Xavier 初始化（有效降低了输入维数为 1 的标量 hint 的初始权重），而在其他地方恢复使用默认的 LeCun 初始化。这种初始化的组合对于本文模型在长期轨迹上的初始学习稳定性非常重要。与此相关的是，在初步实验中，我们看到了学习稳定性的显著改善以及验证性能的显著提高，作者随后在所有实验中都使用了梯度剪裁。

其次是在编码器和解码器部分的改进：

随机位置标量

在这个数据集的所有算法中，存在唯一索引节点的位置标量输入，值沿节点索引线性间隔在 0 和 1 之间。为避免在训练期间过度拟合这些线性间隔值，要将它们替换为随机值，在 中均匀采样，并排序以匹配线性间隔值所隐含的初始顺序。这种变化的好处在算法中很明显，因为很容易过拟合这些位置（例如字符串匹配）。也就是说，即使在测试时 和 将增加 4 倍，该模型也可以学习将所有计算建立在一个假设上，即它将始终在 个字符的字符串中找到 个字符的模式。

排列解码器和 Sinkhorn 算子

排序算法总是输出输入节点的排列，在 CLRS 基准中，此排列被编码为指针，其中每个节点按排序顺序指向其前一个节点（第一个节点指向其自身）。与所有类型的指针一样，这种排列指针可以在无约束解码器输出(logits)上使用逐行 softmax 进行预测，并使用交叉熵进行训练。然而，这并没有明确利用指针编码排列这一事实，相反，模型必须学习该排列。我们的早期实验表明，该模型经常无法预测 OOD 的有效排列。

因此，需要在排序算法的输出解码器中强制实施排列归纳偏差，具体如下：

• 首先，我们通过重新连接第一个节点以指向最后一个节点来修改输出表示，将 P 转换为排列矩阵，即其行和列为单热点向量的矩阵。还使用指定第一个节点的大小为 n 的一个热点向量来增加表示，因此我们不会丢失该信息；该向量被视为常规的 mask_one 特征。

• 其次，我们通过将常用的逐行 softmax 替换为 Sinkhorn 算子 ，从无约束解码器输出 预测置换矩阵 。 过对行和列进行指数化和重复归一化，将任意方阵 投影到双随机矩阵 （一个行和列相加为1的非负矩阵）中，使它们相加为 1。其中 的定义如下面公式 2：

其中，exp 是按元素进行操作， 和 分别表示行和列归一化。

最后是对于处理器网络模块的改进：

门机制

许多算法只需要在每个时间步更新几个节点，其余的保持不变。然而，我们使用的 MPNN（等式 1）偏好相反：它更新每一步中的所有隐藏状态。虽然理论上网络可以保持状态不变，但学习这样做并不容易。考虑到这一点，并受其在 NDR 中的有效性的推动，我们用一个更新门来增强网络，默认情况下偏向于关闭。我们发现门函数可以稳定许多任务的学习，并显著提升单任务训练中所有任务的平均性能。然而，我们却没有发现门函数在多任务情况下有优势。

为了向 MPNN 模型添加门函数，我们从处理等式 1 embedding 的相同输入中生成每个节点的门向量，如公式 3 所示：

处理后的门 embedding 计算如公式 4 所示，用于替换掉公式 1 的部分内容 :

三重推理

CLRS-30 中的几个算法明确要求基于边的推理——其中边存储值，并基于其他边的值进行更新。即使在上述更新中没有节点表示，我们所有的处理器还都集中于在节点表示 之间传递消息。

为了纠正这种情况，我们增强了处理器以执行向边传递消息。可以通过选择中间节点，然后在所有可能的选择上聚合来更新边表示。因此这里引入了三元组推理：首先，在三元组节点上计算表示，然后对一个节点进行约简得到边的隐向量，如公式 5 所示：

其中， 是三元组消息函数，将所有相关表示映射到每个节点三元组的单个向量， 是边读出函数，其为每条边转换聚合三元组以供以后使用。

需要注意的是，计算三元组表示一直是一般 GNN 设计中的有用方法，但它主要是在 GNN 的背景下对恒定输入特征进行研究的。本文的研究是首个验证它们在具有明确初始特征的推理任务中的有效性的研究之一。

多任务改进

在多任务实验设置中，我们在所有 CLRS-30 任务中训练单个处理器，batch size 和学习率与单任务实验中的相同，在这里将每个任务的编码器和解码器分开。

为了执行更新，可以在单步执行优化器之前从所有任务中累积梯度，或者在每个算法的每个 batch 处理后独立地单步执行。这两种方法在多任务学习任务中都被认为是有效的，并且根据经验发现，在本文的设置中，每个任务单独执行会产生更好的结果。在最近的工作之后，我们没有探索专门的多任务优化器，但正如已经描述的那样，通过梯度裁和标量 hint 编码器的 Xavier 初始化来确保训练的稳定性，以改善爆炸输出和 NaN 梯度。由于发现门函数会降低多任务性能，因此它未应用于多任务模型中。

此处对多任务实验的改进如下：

分块

为了减少多任务训练的内存占用，这里实现了分块训练模式，其中轨迹沿时间轴被分割以进行梯度计算，当它们小于块长度时，将与后续轨迹连接，以避免填充的需要。因此，虽然标准训练 batch 由完整的轨迹组成，并填充到最长的轨迹的长度，但分块训练 batch 具有固定的时间长度（在实验中为16步），并由轨迹段组成，在一个轨迹结束后，紧接着是另一个轨迹的开始，因此没有填充。

每个分块 batch 的损失是独立计算的，梯度不能在块之间流动。由于输出损失仅在每个轨迹的最终样本上计算，因此如果一个块不包含轨迹结束段，则它可能不会产生输出损失。因此，分块会根据轨迹的长度改变 hint 和输出损失之间的平衡。

实验结果

单任务结果

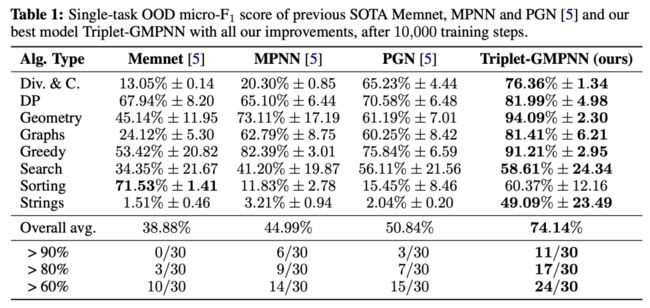
通过结合上述改进，我们得到了一种具有单一参数集的单一模型，该模型经过训练后在 CLRS-30 上达到了新的 SOTA 性能。表 1 和图 2 显示了本文模型 Triplet-GMPNN（带有门和三元边处理的 MPNN）的 micro-F1 分数，图 2 显示了改进后的模型与最佳 baseline 模型之间的比较。

▲表 1 本文最佳模型 Triplet-GMPNN 的单任务 OOD micro-F1 分数

与表 1 中的次优模型相比，先前的改进使总体平均性能提高了 20% 以上(绝对而言)；并且与其他所有模型相比，除一个算法系列外，其他所有算法系列的性能都有显著提高。

▲图 2 改进前后单任务实验中的 OOD 性能

此外，这里的稳定改进（如梯度裁剪）根据经验减少了模型在 30 个任务中的梯度更新规模，使我们更好地应对多任务状态的数字问题。最后，我们还注意到，尽管没在表 1 和图 2 中显示出来，但对 PGN 处理器应用相同的改进，可以将整体性能从表 1 中的 50.84% 提高到 69.31%。

有两个显着的 OOD 性能改进的算法系列示例：第一种是几何算法（Segments Intersect、GrahamScan 和 Jarvis' March），现在解决了大约 94% 的 OOD，而之前的最佳解决方案约为 73%；第二个是字符串算法（Knuth-Morris-Pratt 和 Naïve String Matcher），本文模型现在超过49%，而之前的最佳值约为 3%。

与之前的 SOTA 相比，本文模型显著的整体性能提升体现在算法数量的增加上，现在可以解决超过 60%、80% 和 90% 的 OOD 性能。具体来说，现在有 24 种算法（之前有 15 种算法）的准确率超过 60%，17 种算法的准确率超过 80%（之前有 9 种），11 种算法的准确率超过 90%（之前有 6 种）。

多任务结果

下图 3 比较了单任务 Triplet-GMPNN 与多任务模型的性能，其中 ST 是单任务，MT 是多任务。

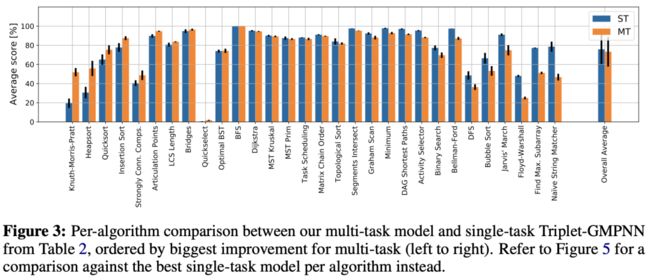▲图 3 多任务模型与单任务 Triplet-GMPNN 间的逐算法比较

对于多任务实验中分块的改进，在图 4(a) 中可以看到，经过分块训练后，所有 30 个任务的平均多任务性能明显优于全轨迹的训练。

▲图 4 多任务模型消融结果

图 5 还显示了与表 2 中最佳算法单任务模型的其他比较，以及多任务模型性能与单任务模型性能相匹配或超过其性能的任务数量的解释。

▲表 2 与以之前 SOTA Memnet、MPNN 和 PGN 的单任务 OOD 比较 ▲图 5 多任务模型与表 2（图 5a 和 5b）中每个算法的最佳模型比较

通过下图可以了解到，只有一种算法 Bellman-Ford 在分块训练时性能较差。分块对多任务学习性能的显著影响表明：优化过程中不同任务的 hint 和输出损失权重对多任务学习的成功至关重要。

▲分块和非分块多任务模型的算法比较

最后，将单任务和多任务结果与相关算法子集上的多任务训练进行了比较，如下图所示。

▲多任务和单任务训练与相关算法子集训练的算法比较

小结

与现有的大多数技术不同，本文的关键结论是：以多任务方式学习不同的算法确实是可能的，但需要仔细注意 GNN 的学习动态和稳定性。此外，如果在适当的通用性水平上对 GNN 架构、数据流程或损失函数进行修改，则有可能一次性提高大型算法组的算法执行性能。最后，分块在多任务机制中获得的显著改进表明：在 hint 优化的有效性方面，还有许多有趣的途径有待未来探索，以及尤其是在多任务算法学习机制中，如何与下游输出预测相平衡的这一问题值得探索。

卖萌屋作者：智商掉了一地

北理工计算机硕士在读，近期沉迷于跟 ChatGPT 唠嗑，对一切新颖的 NLP 应用充满好奇，正在努力成为兴趣广泛的斜杠青年～

作品推荐

1. 我是粉红猪佩奇，我要把粉色吹风机写进 IJCAI 论文！

2. AI取代人类，可以自动生成prompt了

3. ICLR 2023 最高分论文被锤抄袭？？

4. AI讲话总爱“结巴”？这篇NeurIPS论文找到了病因，结巴率已接近人类！

5. 如何提升大规模Transformer的训练效果？Primer给出答案

6. Yoshua Bengio：我的一生

后台回复关键词【入群】

加入卖萌屋NLP、CV、搜推广与求职讨论群