《机器学习基石》学习笔记 8 Noise and Error
上一节课,我们主要介绍了 VC Dimension 的概念。如果 Hypotheses set 的 VC Dimension 是有限的,且有足够多 N 的资料,同时能够找到一个 hypothesis 使它的 E i n ≈ 0 E_{in} \approx 0 Ein≈0,那么就能说明机器学习是可行的。本节课主要讲了数据集有 Noise 的情况下,是否能够进行机器学习,并且介绍了假设空间 H 下演算法 A 的 Error 估计。
一、Noise and Probablistic target
上节课推导 VC Dimension 的数据集是在没有 Noise 的情况下,本节课讨论如果数据集本身存在 Noise,那 VC Dimension 的推导是否还成立呢?
首先,Data Sets 的 Noise 一般有三种情况:
- 由于人为因素,正类被误分为负类,或者负类被误分为正类;
- 同样特征的样本被模型分为不同的类;
- 样本的特征被错误记录和使用。

之前的数据集是确定的,即没有 Noise 的,我们称之为 Deterministic。现在有 Noise 了,也就是说在某点处不再是确定分布,而是概率分布了,即对每个 (x,y) 出现的概率是 P ( y ∣ x ) P(y|x) P(y∣x)。
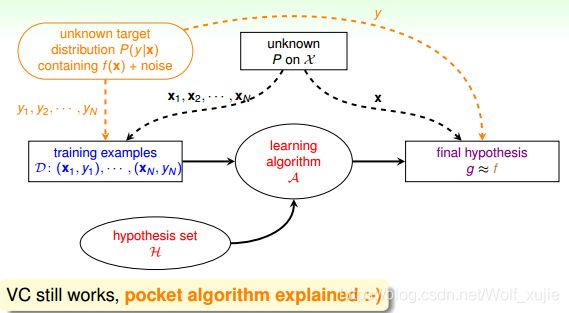
因为 Noise 的存在,比如在 x 点,有 0.7 的概率 y=1,有0.3的概率 y=0,即 y 是按照 P ( y ∣ x ) P(y|x) P(y∣x) 分布的。数学上可以证明如果数据集按照 P ( y ∣ x ) P(y|x) P(y∣x) 概率分布且是 iid 的,那么以前证明机器可以学习的方法依然奏效,VC Dimension 有限即可推断 E i n E_{in} Ein 和 E o u t E_{out} Eout 是近似的。

P ( y ∣ x ) P(y|x) P(y∣x) 称之为目标分布(Target Distribution)。它实际上告诉我们最好的选择是什么,同时伴随着多少 noise。其实,没有 noise 的数据仍然可以看成“特殊”的 P ( y ∣ x ) P(y|x) P(y∣x) 概率分布,即概率仅是 1 和 0。 对于以前确定的数据集:
P ( y ∣ x ) = 1 , f o r y = f ( x ) P(y|x)=1,for \ y=f(x) P(y∣x)=1,for y=f(x)
P ( y ∣ x ) = 0 , f o r y ≠ f ( x ) P(y|x)=0,for \ y≠f(x) P(y∣x)=0,for y=f(x)
二、ERROR Measure
机器学习需要考虑的问题是找出的 g 与目标函数 f 有多相近,我们一直使用 E o u t E_{out} Eout 进行误差的估计,那一般的错误测量有哪些形式呢?
我们介绍的 g 对错误的衡量有三个特性:
- out-of-sample:样本外的未知数据
- pointwise:对每个数据点x进行测试
- classification:看prediction与target是否一致,classification error通常称为0/1 error
PointWise error 实际上就是对数据集的每个点计算错误并计算平均, E i n E_{in} Ein 和 E o u t E_{out} Eout 的 pointwise error 的表达式为:
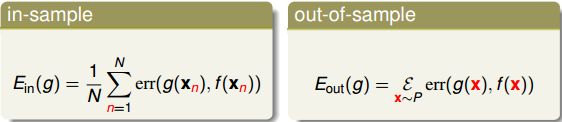
pointwise error 是机器学习中最常用也是最简单的一种错误衡量方式,未来课程中,我们主要考虑这种方式。pointwise error 一般可以分成两类:0/1 error 和 squared error。0/1 error 通常用在分类(classification)问题上,而 squared error 通常用在回归(regression)问题上。

Ideal Mini-Target 由 P ( y ∣ x ) P(y|x) P(y∣x) 和 err 共同决定,0/1 error 和 squared error 的 Ideal Mini-Target 计算方法不一样。例如下面这个例子,分别用 0/1 error 和 squared error 来估计最理想的 mini-target 是多少。0/1 error 中的 mini-target 是取 P ( y ∣ x ) P(y|x) P(y∣x) 最大的那个类,而 squared error 中的 mini-target 是取所有类的加权平方和。

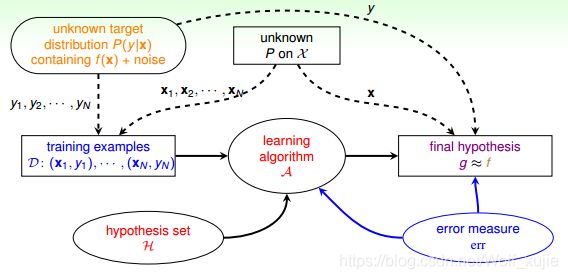
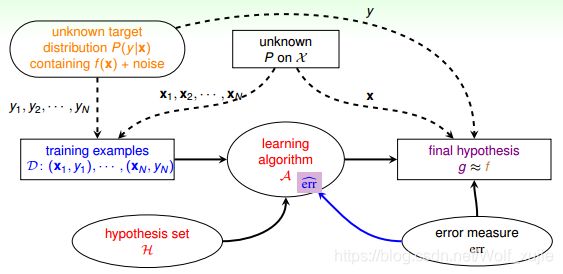
有了错误衡量,就会知道当前的 g 是好还是不好,并会让演算法不断修正,得到更好的 g,从而使得 g 与目标函数更接近。所以,引入 error measure 后,学习流程图如下所示:
三、Algorithmic Error Measure
Error 有两种:false accept 和 false reject。false accept 意思是误把负类当成正类,false reject 是误把正类当成负类。 根据不同的机器学习问题,false accept 和 false reject 应该有不同的权重,这根实际情况是符合的,比如是超市优惠,那么 false reject 应该设的大一些;如果是安保系统,那么 false accept 应该设的大一些。

机器学习演算法 A 的 cost function error 估计有多种方法,真实的 err 一般难以计算,常用的方法可以采用 plausible 或者 friendly,根据具体情况而定。

引入 algorithm error measure 之后,学习流程图如下:
四、Weighted Classification
实际上,机器学习的 Cost Function 即来自于这些 error,也就是算法里面的迭代的目标函数,通过优化使得 Error( E i n E_{in} Ein)不断变小。
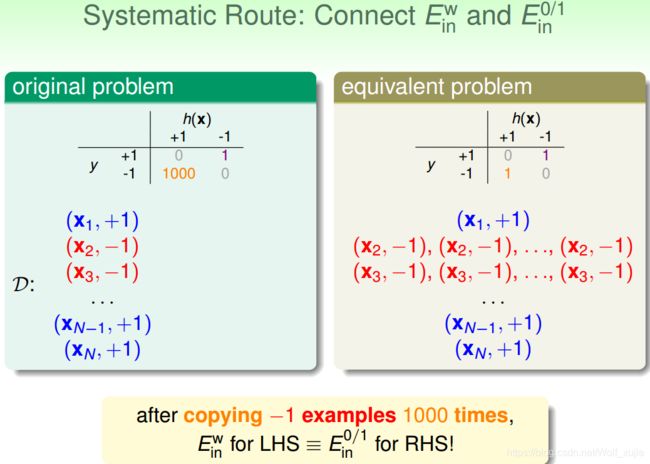
cost function 中,false accept 和 false reject 赋予不同的权重,在演算法中体现。对不同权重的错误惩罚,可以选用 virtual copying 的方法。
总结
本节课主要讲了在有 Noise 的情况下,即数据集按照 P ( y ∣ x ) P(y|x) P(y∣x) 概率分布,那么 VC Dimension 仍然成立,机器学习算法推导仍然有效。机器学习 cost function 常用的 Error 有 0/1 error 和 squared error 两类。实际问题中,对 false accept 和 false reject 应该选择不同的权重。