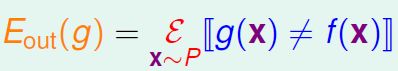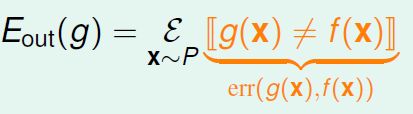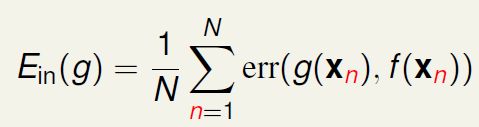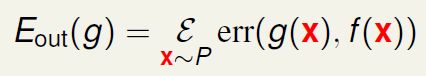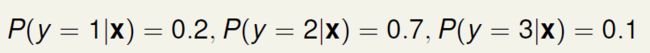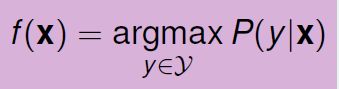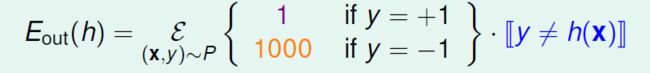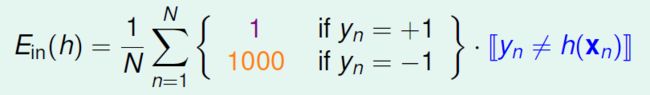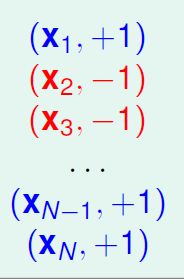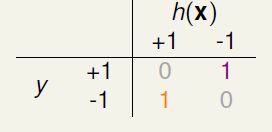林轩田《机器学习基石》(八)—— Noise and error
上一节课,我们主要介绍了VC Dimension的概念。如果Hypotheses set的VC Dimension是有限的,且有足够多N的资料,同时能够找到一个g使它的![]() ,那么就能说明机器学习是可行的。
,那么就能说明机器学习是可行的。
之前我们说过含noise的问题,现在我们看加上noise会不会对整个推导有影响?即VC bound还会不会作用的很好?
一、噪音:noise
我们看一下带noise的学习问题的流程图:
资料的noise主要来源有(以信用卡为例):
1.标签y的noise,比如一个好顾客有坏标签
2.标签y的noise,比如顾客的特征都相同但是标签却不一样。
3.资料x的noise,比如顾客信息不精确
之前的数据集是确定的,即没有Noise的,我们称为Deterministic。现在有Noise了,也就是说在某点处不再是确定分布,而是概率分布了,即对每个(x,y)出现的概率是P(y|x)。
我们仍拿罐子中的球做类比,那么之前的球要么是橙色,要么是绿色,noise的球就是不固定某种颜色了,而是某概率是橙色,其余概率是绿色。(我们要求y也是要取样来的,其实就是颜色y服从某个分布P(y|x))
现有
上述可以被证明,解释一下上面的:如果在训练和测试,对每个资料x,有 ,对于相应的y有
,对于相应的y有 ,
,
那么整个的VC结构还是会作用的很好。(即文章开头的红色字部分还是成立的)
我们今天要讲的是“分布”——对于一个x,我们可以做一个预测,最理想的预测是什么?
P(y|x)称之为目标分布(Target Distribution)。它实际的预测结果是告诉我们理想预测以及noise。
比如对于某x,有
可以看出他理想预测是‘o’,并且它的noise的概率是0.3.
而对于deterministic target f来说(无noise的情况),可以看做是一种特殊的目标分布 : 、
如果一笔资料常常被抽样到,那么它即出现在![]() ,也出现在
,也出现在![]() ,所以我们是希望他表现好的。
,所以我们是希望他表现好的。
继续回到带noise的学习流程图:
二、误差度量
机器学习需要考虑的问题是如何证明g与目标函数f很像,我们一直使用![]() 进行误差的估计,
进行误差的估计,
那一般的误差度量有哪些形式呢?
g对于误差度量来说,有以下几个特性:
1.不知道未抽样出的x
2.pointwise:我们可以在每一个x上进行单独的衡量,不需要抽一堆后才能衡量。
3.分类:看看预测与目标是否不一致,通常叫做0-1误差。
我们做的误差度量可以像之前一样,考虑每个点上有多少错误,然后逐点相加。
我们把每个点上的误差记作err
所以在已知样本上:
在未知样本上:
我们现在讨论一下有哪些逐点误差(简要记作![]() 和
和![]() 的误差):
的误差):
0-1误差
主要判断标签是对是错,通常用于分类问题。
平方误差
主要判断标签与正确答案之间距离多远,通常用于回归问题。
为什么考虑不同误差呢?因为分布以及我们对误差的度量会影响到target f。
举一个例子:
对于0-1误差:
我们选取![]() =1,2,3,其他(比如1.9)四种情况,来看结果产生的平均误差是多少
=1,2,3,其他(比如1.9)四种情况,来看结果产生的平均误差是多少
可以看到结果最好的是![]() 的时候,而且我们会觉得
的时候,而且我们会觉得![]() 很不可思议。但是在下面的平方误差中却是最好的选择:
很不可思议。但是在下面的平方误差中却是最好的选择:
对于平方误差:
我们同样选取![]() =1,2,3,其他(比如1.9)四种情况,来看结果产生的平均误差是多少
=1,2,3,其他(比如1.9)四种情况,来看结果产生的平均误差是多少
我们在数学式子上可以证明的target f与目标分布P的关系:
对于0-1误差:
对于平方误差:
综上,我们希望告诉我们用什么度量误差,我们知道机器学习看重什么,才能更好地评价g。
三、算法的误差度量
误差度量是怎么来的呢?(或者说该如何选择呢?)
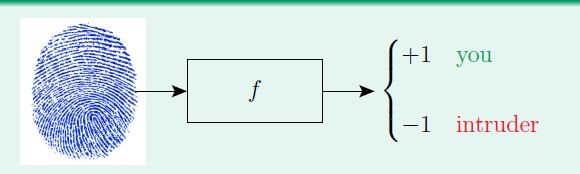
比如一个指纹识别的实际例子中:
Error有两种:false accept和false reject。
false accept意思是误把负类当成正类,本来这个指纹是不能用的,但电脑说它能用。
false reject是误把正类当成负类,本来这个指纹可以用,但是电脑拒绝了它。
根据不同的机器学习问题,false accept和false reject的侧重不同。
比如在超市打折系统中
false reject:本来顾客的指纹可以用,电脑总是拒绝,那么顾客会不开心,损失客人!
false accept:本来不能用,现在却允许了,给这个顾客有了折扣,没什么关系就是少赚点钱。
所以false accept和false reject的成本表为:
在CIA中
false accept:本来没有权限进入,但现在被允许进入,可能涉及泄密,很危险!
false reject:进入者不被允许,不开心,但那又没什么关系:-)
所以false accept和false reject的成本表为:
不同的应用适合不同的err。所以在设计算法时,要想办法加入err的设计,考虑到真实的err没办法像成本表一样准确衡量,所以设计时常常用近似![]() 代替err,有两种方法:
代替err,有两种方法:
plausible方法:
1.0-1误差:极小化flipping noise’
2.平方误差:极小化Gaussian noise
friendly方法:容易设计算法
1.容易求闭式解
2.目标函数为凸
四、有权重的分类
我们看有权重的分类,即我们更加不希望“把负样本分类为正样本”这种错误发生。于是之前的
在未知样本上:
在已知样本上:
我们要怎么解这样的问题?
我们还是让![]() 越来越小,现在将
越来越小,现在将![]() 记作
记作![]() 。
。
考虑下面两种算法:
PLA:如果线性可分,那么总有一个分类会分的完全正确使得![]() =0, 所以加不加权没有影响。
=0, 所以加不加权没有影响。
pocket方法:如何使它的![]() 尽可能小?它之前的思路在于:如果新找的w“好”,那就把最新的w放入口袋。我们希望从这里找到突破口,我们希望现在的“好”,不再是比有几个对几个错,而是换算为加权后的。
尽可能小?它之前的思路在于:如果新找的w“好”,那就把最新的w放入口袋。我们希望从这里找到突破口,我们希望现在的“好”,不再是比有几个对几个错,而是换算为加权后的。
比如之前的成本表:
之前的数据:
由于我们更加不希望“把负样本分类为正样本”这种错误发生,所以这种犯错成本高,于是我们把负样本复制1000倍,这样一旦有一个分错,他复制的这1000个点也会犯错。
于是现在的成本表变为:
新的数据集变为
从成本表看出此时的误差度量变为了0-1误差。
上面的这种方法叫做virtual copying。
在实际中我们通常不会真的复制那么多次,我们可以让“更严重的错误”的样本点(比如上面的负样本点)被更频繁的拜访,感觉这样改变了资料的分布。
总结: