公开课 | 机器学习基石08 Noise and Error
前面几篇通过引入 VC 理论证明了机器学习的可行性。讨论的数据都是无噪音的,但实际数据,噪音往往不可避免。 本篇是承上启下的一篇,连接了理论部分和后续具体的机器学习演算法,容易被忽略,个人觉得是非常重要的一篇。介绍了 noise 和 error 两个核心概念。讲解即便 noise 存在的情况下,绝大部分 H 和 err,VC 理论同样适用。
先回顾在没有 Noise 情形下的机器学习模型。
VC 理论证明机器学习是可行的。所谓机器学习可行,通俗理解:可以找到 hypothesis g, Eout(g) 足够小。
上图不等式 (VC Bound) 揭示了 Eout 被 Ein + Ω (模型的复杂度) bound。
为了使 Eout 足够小,可以分别让 Ein 和 Ω 足够小。
下面分析一下,如何让 Ein 和 Ω 足够小( trade-off)。
1. Ein 的角度。H 的 d_vc 越高,模型的表达能力越强,越有机会使得 Ein 足够小,所以 Ein 随着 d_vc 的增高而下降。也可以从自由度的角度思考,d_vc 越高,模型的自由度越高,模型越能拟合训练集,自然可以做到 Ein 足够小。单纯从 Ein 的角度而言,希望 d_vc 足够大。
2. Ω 的角度 (模型复杂度,与 N、H、δ 相关)。从表达式可以看出,要使得 Ω 足够小,d_vc 不能太大 (至少是有限的),N 足够大。这解释了如果 H 的 d_vc 较大,希望 N 能够更大,中和一下模型的复杂度( Ω )。前面也说过,理论上要求 N ≈ 10,000 d_vc (实践 N ≈ 10 d_vc)。
结论( d_vc 的权衡 ):d_vc 越大,表明模型的表达能力越强,但模型的复杂度也随之上升。
一图胜千言:
虽然一直说机器学习是可行的,可行是有条件的,需要万事俱备 (good H, good D, good A)。
1. good H:H 的 VC 维不应太大,至少是有限的 (等价结论 H 有 break point)。
2. good D:满足 i.i.d 并且 N 足够大 ( 理论:N ≈ 10,000 d_vc,实践:N ≈ 10 d_vc)。
3. good A:H 的 VC 维不应太小,还需要一点点运气哦,使得 Ein 足够小。
以上,是我的理解,轻拍砖。
目前的 VC 理论是有缺陷,主要表现在如下两个方面:
1. 如果数据中存在 noise。
2. Error Measure 没有说清楚。
3. 目前考虑的是二分问题。如果是回归问题是否有效?
本篇意在说明前两个问题,问题 3 下一节课介绍。
Noise 的产生
noise 无处不在,以“是否给用户发信用卡”为例。
大体分为两类:
noise in y
noise in x
Probabilistic Marbles
noise 的加入,导致原 marbles 模型,需要加以修正 (probabilistic)。
确定 vs. 随机 (deterministic marbles vs. probabilistic marbles)。
1. x ~ P(x) (i.i.d)。两种模型均要求来自某特定分布( i.i.d,来自 target function)。
2. probabilistic marbles 要求 y ~ P(y|x),y 来自某特定分布[y ~ i.i.d],综合: (x, y) ~ P(x, y)。
3. probabilistic marbles 预测的不是 target function,而是 target distribution,即 P (y|x), 直观解释:f(x) 有多大可能是 y。
target distribution P(y|x) 的理解
target function 是 target distribution 的特殊情况 (非此即彼)。
P(f(x) | x) ≡ 1。具体分为两种情况:
1. P(y|x) =1 for y = f(x),
2. P(y|x) =0 for y ≠ f(x)
noise 会导致 “同样的 x,不同的 y”。这时候只能考虑 P(y|x),即:在 x 条件下 为 y 的概率。
举个例子。假设 P(o|x) = 0.7, P(x|x) = 0.3。
直观上理解,在同样 x 前提下,为 o 的概率是 0.7,x 的概率是 0.3。如果让你决策, f(x) 你选啥?估计多半会选择 f(x) = o,依据是倾向于选择概率大的那个 y 作为 f(x)。
选择了 f(x) = o,那么为什么 P(o|x) 不等于 1?自然可以理解为受 noise 的影响。
感性理解:target distribution 被分为两部分: target(主要部分,被称为 mini-target) + noise (噪音影响)。
1. ideal mini-target。选择 P(y|x) 最高的 y 作为 f(x)。比如例子中:f(x) = o。
2. 'flipping' noise level 。比如例子中 noise = 0.3。
那么机器学习的目标变为【直观理解】:f(x) 选择那些数据集中经常看到值(概率大)。
"predict ideal mini-target(w.r.t P(y|x)) on often-seen inputs(w.r.t P(x))"
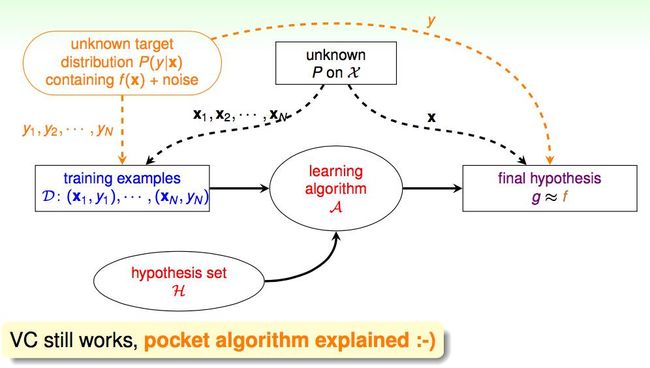
The New Learning Flow
数据来自于 target distribution P(y|x), Flow 的其他部分按完全一致。target distribution 和 target function 基本也没什么两样,几乎可以用 target distribution 代替 target functon, 把 VC 公式重新写一遍 (直观理解:target distribution 是 target function 的某一瞬间值,严格推导我也不会,囧)。
机器学习中,满足一些条件,促使 Eout 很小,就认为机器学习可行。但一直以来并没有仔细研究过错误衡量 (Error Measure)。
Error Measure 引入的目的是为了衡量机器学习演算法最终选择的 g 是否真的很好,即在 out-of-sample 中评价 g 的好坏 (直观理解:就是给 g 打分数)。
E(g, f) 的一些设计原则:
1. out-of-sample 通常采用期望值。
2. 简单的统计方法,采用逐点 (pointwise error measure) 计算。就是看 g 在每个点上的表现。当然并意味着 E(g, f) 必然是 pointwise 的,通常即为 err。
3. 之前讨论的分类问题,采用的是 E(g(x)≠f(x)) (非此即彼,也是 pointwise) ,通常称为:0/1 error( 即为 E^0/1)。
重点讨论 pointwise 的方式。
Pointwise Error Measure
定义如下:
pointwise error measure 通常记为 err。利用 err 很容易计算 Ein 和 Eout,如下图所示。
实际应用中,两种常用的 err。
0/1 error: 常用于分类问题。
squared error:常用于回归问题。
有了 err (pointwise error),终于可以实现(定义)逐点选择理想的 mini-target 了。
ideal mini-target f(x)
P(y|x) 是 i.i.d,那么针对某个点(pointwise) 如何选择 target f(x) 呢?
不难想到,可以选择 err 最小的那个值。现在终于知道 mini-target 中 mini 的含义了吧 (mini-error)。
举个例子。指定 x,分布如下:
1. 如果采用 0/1 error。自然选择 f(x) = argmax(P(y|x))。
2. 如果采用 squared error。
假设 f(x) = 1.9。
err(f(x), y) = ∑p(y|x) (f(x)-y)^2
= P(1|x)*(1.9-1)^2 + P(2|x)*(1.9-2)^2 + P(3|x)(1.9-3)^2
= 0.9*0.9*0.2 + 0.1*0.1*0.7+1.1*1.1*0.1
=0.29
其实 mini ∑p(y|x) (f(x)-y)^2 ,就是当 f(x) 导函数为0时最小,不难得出答案。
这个例子可以看出:err 关乎 mini-target f(x) 的选择,不同 err 可能导致选择不同 mini-target f(x)。
Learning Flow with Error Measure
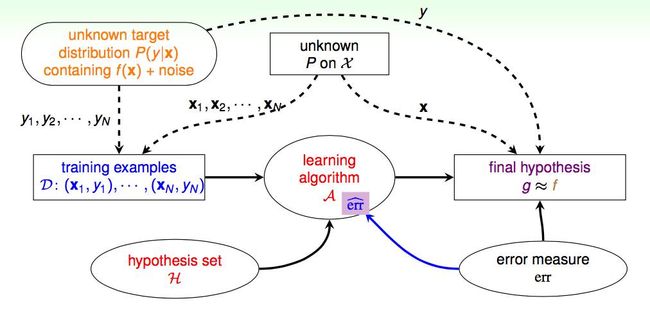
现在可以将 error measure 加入 Learning Flow 中(之前已经用了 0/1 error,只是一直没有强调)。
error measure 的不同,会影响到 mini-target f 的选择。所幸的是,对于绝大多数的 H 和 err, VC 理论同样适用("extended VC theory works for most H and err")。
太深奥了,不细究了。下一讲会讲到,将 Linear Regression 用于 Linear Classification 时候,使用 squared err,可以证明 VC 理论是有效的,敬请期待。
以指纹识别为例 - 0/1 err。
在 0/1 err 中,错误只有两种,即:false accept 和 false reject。
这两种错误的成本是相同的,但是实际问题中,情况并非如此。比如:CIA,明显 false accept 成本更高。这样自然可以想到成本矩阵。
error measure 往往需要考虑实际情形,将这类 error 称为 algorithmic error measure, 记为 err^ (读作 err hat)。
常用的一些 err^。
1. 当然 err ⊂ err^ (实际问题也常使用 0/1 err 和 squared err,可见一斑)。err 通常也比较简单合理。
2. 计算方面的考虑。closed-form 和 convex 是不错的选择。
反正记住一句话,对于绝大部分 H 和 err,VC 理论 works。
将 err^ 加入 Learning Flow。
实际的 err 无从得知 (unknown),演算法真正使用的是 err^。
实际应用中,设计 err^ 常用的一种策略,就是 weighted err。本节意在说明 weight err 和 0/1 err 等价。
以 CIA Cost Matrix为例。根据 Cost Matrix 可以定义 weight err。
以 Perception 模型,采用 weighted err 作为 PLA 演算法的错误衡量依然有效。
1. 对于线性可分,PLA 显然 OK的。
2. 如果线性不可分,weighted err 代替 0/1 err,Pocket Algorithm 依然可行。详见下面解释。
假想 false 的 data 被复制(virtual copying) 1000 倍。那么等价问题是 Pocket 在新的数据上,采用 0/1 error 作为错误衡量标准,显然是有效的。所以 weighted err 在原数据集上是有效的。
weighted err 被广泛应用到各种机器学习演算法之中。
小结
本篇承上启下,介绍了 noise 和 error 两个核心概念。即便 noise 存在的情况下,绝大部分 H 和 err 而言,VC 理论同样适用。
下篇开始,将介绍具体的机器学习模型和对应的演算法。
转自:机器学习小蜜蜂
阅读伙伴公众号更多精彩内容,点击 “ 阅读原文 ”