kkt条件的理解_直观理解KKT条件

KKT最优化条件是Karush[1939]，以及Kuhn和Tucker[1951]先后独立发表出來的。这组最优化条件在Kuhn和Tucker发表之后才逐渐受到重视，因此许多情况下只记载成库恩塔克条件(Kuhn-Tucker conditions)

库恩塔克条件(Kuhn-Tucker conditions)是非线性规划领域里最重要的理论成果之一，是确定某点为极值点的必要条件。如果所讨论的规划是凸规划，那么库恩-塔克条件也是充分条件。

本文不对数学公式进行详细推导，而是从直观上对KKT条件进行理解。当然KKT条件与拉格朗日乘子是相关联的，看完本文后，可以参阅相关资料。

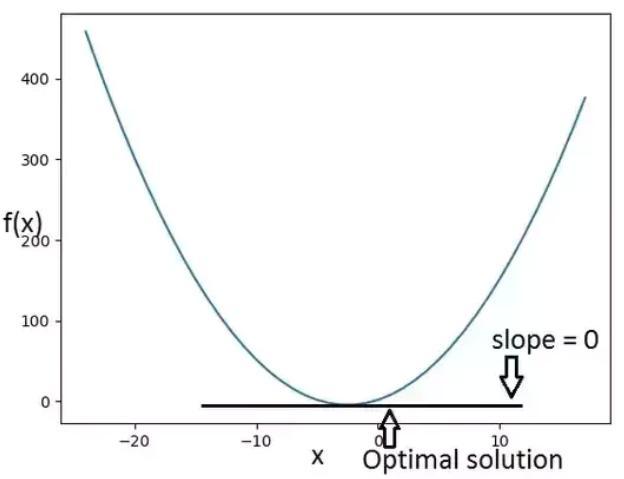
无约束优化问题的极值(函数的最大值/最小值)通常发生在斜率为零的点上。

因此，为了找到极值，我们只需要搜索斜率为零的点。 我们可以用很好的数学形式表达这个属性。

如果 x* 是无约束优化问题的极值， 那么

▽f(x*)=0

等式约束的优化问题

如果x*是等式约束的优化问题的极值, 那么

▽f(x*)=λ×▽g(x*)

g(x*)=0

不等式约束的优化问题

如果x*是不等式约束的优化问题的极值, 那么,

KKT条件:

原可行性:g(x*)≤0对偶可行性: α≥0互补松弛条件:αg(x*)=0拉格朗日平稳性: ▽f(x*)=α×▽g(x*)为了找到具有不等式约束的优化问题的极值，我们需要搜索必须满足所有KKT条件的点(x*)

KKT条件直观理解

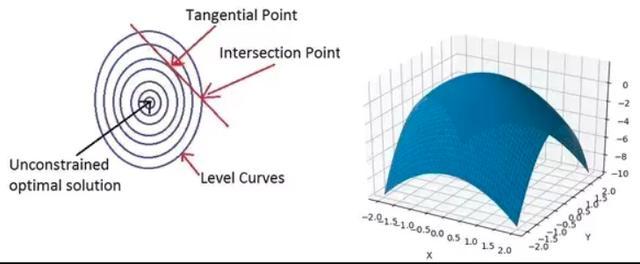
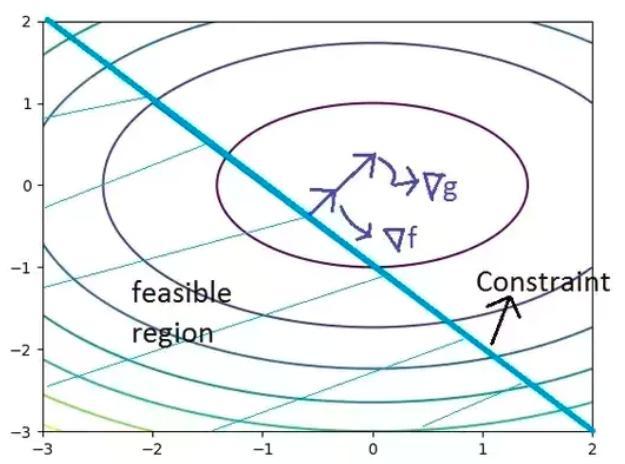
1.拉格朗日平稳性：下面显示了具有等式约束的优化问题的等高线图(它是通过绘制2D格式上的目标函数值的常量切片来表示3D表面的图)。 分析结束后，你会意识到为什么我选择了一个等式约束来解释拉格朗日平稳性条件。

从等高线图中，我们可以推断出上述问题只发生了两种可行点：1、切点2、交点。切点是水平曲线(等高线)和约束线彼此相切的点。 交点是水平曲线和约束线相交的点。

在等高线图中，如果从交叉点(沿约束线)向左移动，则目标函数值会增加。 它表明该问题在这方面有改进的余地。 同样，如果从交叉点向右移动，我们的目标函数值会减小。 但是，对于上图中的切线点，从切线点向右或向左移动只会降低目标函数值。这意味着约束优化问题的极值总是落在切点上。

结论1：约束优化问题的极值总是发生在切点上。

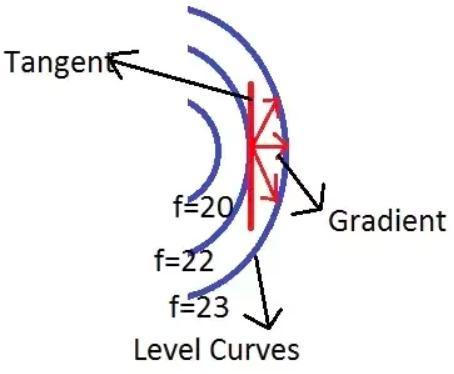
我们知道函数的梯度指向函数增加最大的方向。在下面的等高线图中，从一个水平曲线移动到另一个水平曲线的最短路径是垂直方向，水平曲线与函数中没有立即变化的方向相切。 这意味着任何点处函数的梯度都垂直于该点的函数水平曲线。

结论2：函数的梯度和函数的水平曲线的相切是正交的

通过结合结论1和2，我们可以得出结论，约束的梯度(▽g)和目标函数的梯度(▽f)在极值处(切线点)方向是相同或者相反的。 表达如下：

▽f(x*)=α×▽g(x*)

2. 对偶松弛(α≥0)

α被称为KKT乘子或对偶变量(如果我们将原始问题转换为对偶形式，KKT乘子将成为对偶形式的变量)。在解释KKT乘子只允许非负值的原因之前，让我告诉KKT乘子符号在约束优化问题中的影响是什么.

如果α≥0, 那么 ▽f 和 ▽g 方向是同向的 (▽f(x*)=α×▽g(x*)).

同样，如果α≤0, 那么▽f 和▽g方向是相反的。

例如:

Max 2x22y2 (1)

s.t. x+y≤1

上述问题的最优解是4/3 ，

当x*=2/3 , y*=1/3 and α=4/3。

正如我们在上文看到的那样，拉格朗日乘子对具有等式约束的优化问题没有任何符号限制。但是，对于具有不等式约束的优化问题，KKT乘子是有符号限制的(α≥0)。 你可能会怀疑我们为什么对不等式约束有这个符号限制。在讲KKT乘子只取非负值的原因之前，咱们先来分析下可行域。

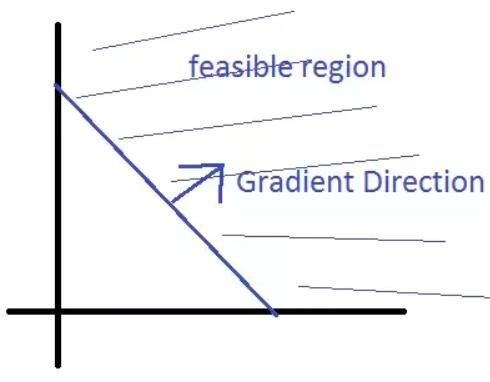
· g(x,y)=0(x+y1=0):可行域仅是一条直线

· g(x,y)≥0:直线上方都是可行域。

· g(x,y)≤0:直线的下方是可行域。

结论3：约束梯度(▽g)始终指向约束控制的可行区域(g(x，y)≥0，g(x，y)≤0方向分别相反)

现在，你可能会理解上述问题中的KKT乘子，只有在可行区域翻转时才会出现负号(i.e.,x+y≥1)。

如果发生这种情况，约束不会对目标函数产生任何影响。 这就像解决一个无约束的优化问题。

Max f(x,y)=2x22y2 (2)

s.t. x+y≥1

最优解: 在点(0,0),f(x,y) 取得最优解2。

这意味着如果约束是活跃状态(下文)，极值发生在▽f和▽g平行的点(α≥0)。 如果它们在极值上不平行，则意味着约束处于非活动状态。

3. 互补松弛条件

α×g(x*)=0

这个条件是说，KKT乘子(对偶变量)或不等式约束(g(x*)≤0)在极值处为零。 我们可以将任何不等式约束分为两类：1、活跃约束2、非活跃约束。

1)活跃约束：极值发生在约束的限制区域(边界)上。 例如：问题1(见式1)最优解在

(x*=22,y*=13) ，约束 g(x*,y*)1=0。

2)非活跃约束：极值发生在可行区域内(不在限制区域的边界上)。例如：问题2(见式2)最优解在

(x*=0,y*=0) ，约束g(x*,y*)1≥0。

从例1中可以看出▽f和▽g平行，α取正值。 在示例2中，我们看到α取负值的情况，导致约束变为非活跃状态。 这意味着

Max f(x)+αg(x)=Max f(x)

只有当α取值为零时，上述情况才有可能。

所以g(x)≠0在极值点处，约束处于非活跃状态