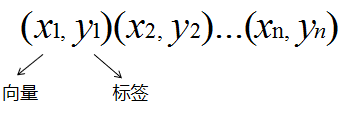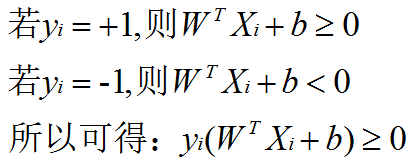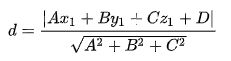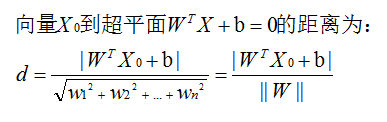python机器学习 | SVM算法介绍及实现
本篇博客具体学习参考：
1 【机器学习】支持向量机SVM及实例应用
2 【ML】支持向量机（SVM）从入门到放弃再到掌握
这两篇文章讲得特别清楚，数学推导（第一篇）也能看明白，强烈推荐学习~~
本篇博文介绍仅在二维展开，以此推展到多维。整体思路大致为：
先整体介绍SVM，然后介绍线性可分样本集下SVM的应用思路是如（重点概念，数学推导）；接着推到非线性可分样本集；最后介绍SVM的api应用和举例实现
SVM算法介绍及实现
- 1 SVM算法介绍-线性可分思路
-
- 1.1 线性可分样本集与非线性可分样本集
-
- 1.1.1 线性可分样本集
- 1.1.2 非线性可分样本集
- 1.2 分类间隔、超平面、支持向量
- 1.3 SVM算法原理/分类应用（数学描述）
- 1.4 例子展示线性可分的超平面计算过程
- 2 SVM算法介绍-非线性可分思路
-
- 2.1 软间隔
- 2.2 核函数
- 3 SKlearn中使用SVM
-
- 3.1 SVM的api介绍
- 3.2 利用SVM进行乳腺癌检测
1 SVM算法介绍-线性可分思路
SVM算法又称为支持向量机，用于分类，优点是适用于小样本和算法优美（此处优美表现在数学推导上）。
那么，其实分类算法我们已经介绍了几种了，先来回顾一下
- 逻辑回归通过拟合曲线（或者学习超平面）实现分类；
- 决策树通过寻找最佳划分特征进而学习样本路径实现分类；
- 朴素贝叶斯是通过特征概率来预测分类。
而现在介绍的SVM（支持向量机）则是通过寻找分类超平面进而最大化类别间隔实现分类；
先来介绍一下SVM算法的分类类型，进而介绍SVM算法中提及的最大间隔，分类超平面，及其实现原理。
1.1 线性可分样本集与非线性可分样本集
1.1.1 线性可分样本集
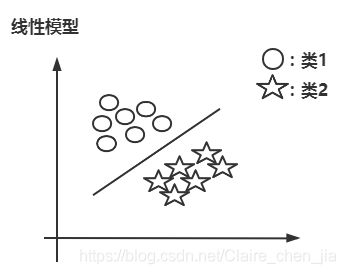
线性可分样本集：只要我们可以使用一条直线将样本集完全分开，如图1.
1.1.2 非线性可分样本集
非线性可分样本集：没有办法直接画一条直线，只能用曲线等模式来分开的样本集，如图2
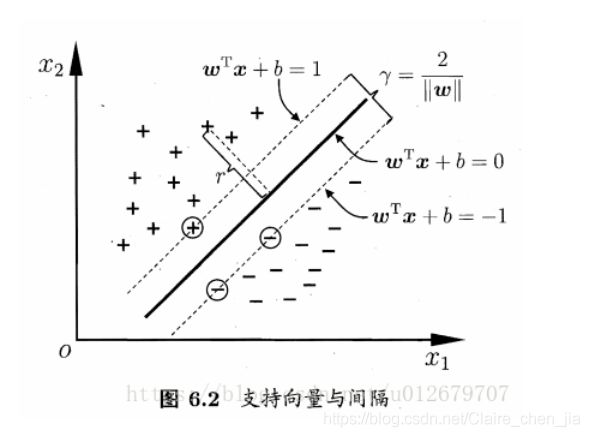
1.2 分类间隔、超平面、支持向量
下面整体的思路就是由线性可分样本集推到非线性可分的问题
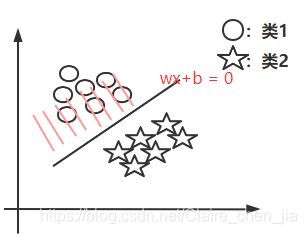
基于线性可分样本集，我们发现只要存在一条直线（一个超平面）可以将类1与类2进行分开。那也就说明实际上有无数条直线（超平面）可以将类1与类2分开。如下图：
那么问题来了：1 选择哪一条直线（超平面）最好呢？
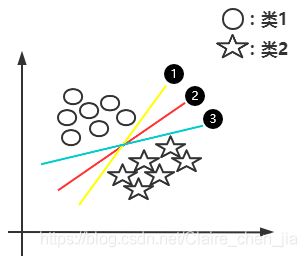
从图中可以得出，在样本统计中，如果我们是允许误差存在的。那么2号线（超平面）的容错度可能更大一点，就是说线2更加robust，这个超平面离直线两边的数据的间隔最大，对训练集的数据的局限性或噪声有最大的“容忍”能力。
接着，问题又来了，怎么取到2号线（2号超平面）的呢？
解答：随机预测出某条线，然后将这条线进行平行移动，直到它交于某一个圈或某几个圈为止；同理，又进行平移，直到交于某几个星为止，这样我们找到两个相交的线，两条相交线的间隔就是最大分类间隔，间隔的中点位置就是2号线位置。如下图：
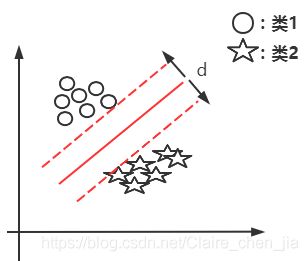
所以，很显然，d越大，也就说明红色实线距离样本点越远，此时容错率也就更高。所以我们的目标为：找分类间隔d最大的线，也就是寻找分类间隔最大的超平面。
-
超平面：在二维中就是一条直线，在多维空间里它是一个N维的，我们可能无法想象，所以定义为超平面。
-
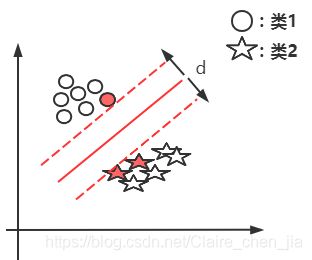
支持向量：支持向量就是将平行线向左右移动，相交的样本点就称为支持向量。如图中的红点。所以也就是说，我们的支持向量机只与支持向量有关，与其它向量无关。
1.3 SVM算法原理/分类应用（数学描述）
在有对 线性可分样本集与非线性可分样本集 、分类间隔、超平面、支持向量的概念后，我们把它翻译为数学语言，并说明SVM算法是如何应用的。
- 定义训练数据和标签
-
xi：向量。实际上是训练数据集的位置。注意这里是向量，不是支持向量，支持向量是离平面最近的点，也就是平面左右平移中第一个与之相交的点。
-
yi：标签
这里的类1：+1，是指在超平面上面，类2：-1，是指在超平面下面。这里是为了方便后面公式推导这样假设的，不影响。 -
超平面：这里再讲一下（观点与上面一样）。那有了这个定义后，假设目标函数为一条直线。已知x,y，则需要求解两个条件：w,b。得到方程如下：
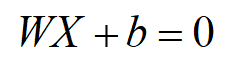
但是实际情况是，我们使用支持向量机解决的问题通常都不是简单的二维问题，而是更高维度的。所以x、w如下：
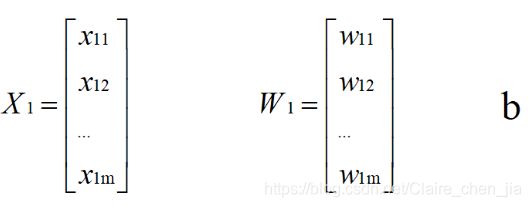
得到超平面模型为：
补充：当f ( x )等于0的时候，x便是位于超平面上的点，而f ( x ) 大于0的点对应 y=1 的数据点，f ( x ) 小于0的点对应y=-1的点。f(x) = wTx + b
- 训练集线性可分的数学定义
二维理解：如图，及如上面的图，1条线把图分为两类，在平面上方>0，在平面下方<0
所以，同理可得对于超平面来说线性可分的定义如下：
- 求解向量到超平面的距离
- 回顾一下点到平面的距离公式：
平面方程为Ax+By+Cz+D=0；点P的坐标(x0,y0,z0)；d为点P到平面的距离公式如下:
同理推导向量到超平面的距离
- 优化目标，利用SVM求出合适的超平面进行分类
- 确定目标
现在我们的目标就是找出所有分类间隔中最大的那个值对应的超平面。而SVM 就是帮我们找到一个超平面，这个超平面能将不同的样本划分开，同时使得样本集中的点到这个分类超平面的最小距离（即分类间隔）最大化。 - 确定计算分类超平面的w和b的目标函数
下面推导过程来自： 【机器学习】支持向量机SVM及实例应用
凸函数形式特点：要么无解，要么只有一个极值。条件为1.目标函数：二次项 2.限制条件：一次项
确定了目标函数，转为凸函数形式的目标函数，我们就要来求w和b了 - 利用拉格朗日乘子法求解w和b，进而求出超平面
1）介绍拉格朗日乘子法
设给定二元函数z=ƒ(x,y)和附加条件φ(x,y)=0，为寻找z=ƒ(x,y)在附加条件下的极值点。
拉格朗日乘子法公式如下：
2）代入式子：将目标函数以及约束条件代入式子。可以得到其对偶问题。具体来说，对式的每条约束添加拉格朗日乘子αi>=0，得到结果如下：
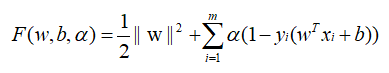
分别对w求偏导为0、与对b求偏导为0，得到结果如下：
消除w和b：
将求解w,b的问题转为了求α最大值的问题，求出α最大值后，代入回去就能计算w和b：
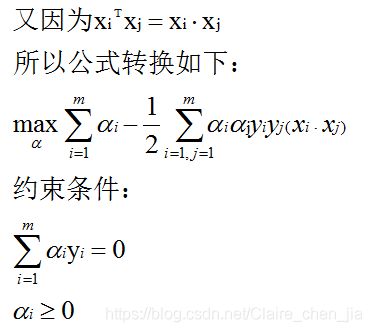
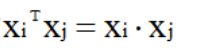
是内积，具体为：
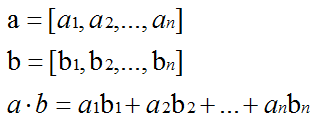
1.4 例子展示线性可分的超平面计算过程
数据：3个点。其中正例X1(3,3),X2(4,3),负例X3(1,1)
目标函数（超平面的公式转为求α最大值的问题）：
约束条件：
（1）αi*yi的和为0
（2）αi>=0 i=1,2,3
那现在，我们就将数据代入到目标公式：
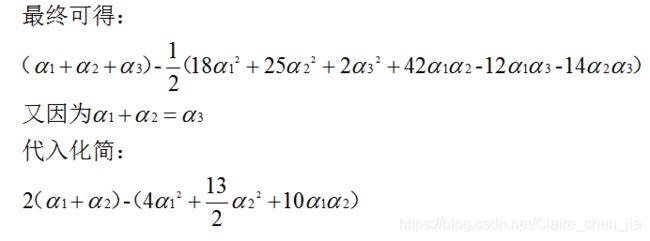
那整个式子只与α1、α2有关。那我们需要将整个式子求解最大值。我们也转换为求极小值。
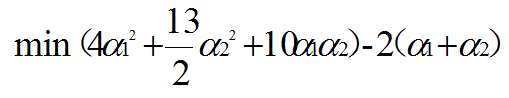
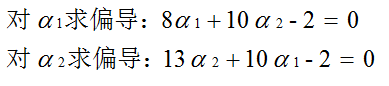
但是α2<0是不符合约束条件的。所以我们需要的这个解不在偏导为0的位置。思考，处于α1=0或者α2=0的边界位置上。
现在求得了α之后，我们其实是需要求解w,b的。
2 SVM算法介绍-非线性可分思路
下面我承线性可分思路，继续将非线性可分思路。
具体关于非线性可分思路的推导可以学习： 【机器学习】支持向量机SVM及实例应用
本节只是做到把抽象概念形象化
2.1 软间隔
- 软间隔：假如数据是完全的线性可分的，那么学习到的模型可以称为硬间隔支持向量机。换个说法，硬间隔指的就是完全分类准确，不能存在分类错误的情况。软间隔，就是允许一定量的样本分类错误
当容忍一些样本分类错误的线性可分模型，我们可以称为近似线性可分。如下：
那为了使样本分类不那么严格，我们引入了松弛因子。构建新的目标函数：
C为常数项，C的右边部分为松弛因子。当常数项越大，松弛因子越小，说明软间隔越小，相反，则软间隔越大。
同时，新的目标函数就是我们讲的“软间隔支持向量机”
2.2 核函数
对于非线性样本集，不论多么高级的线性分类器，都无法处理。
这时，我们需要引入一个新的概念：核函数。它可以将样本从原始空间映射到一个更高维的特质空间中，使得样本在新的空间中线性可分。这样我们就可以使用原来的推导来进行计算，只是所有的推导是在新的空间，而不是在原来的空间中进行。
图示：
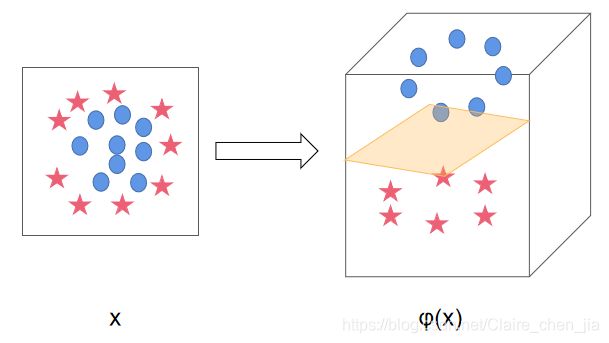
我们可以形象地理解为：桌子上零散地放着核桃和腰果两种零食，我们要把它分类。那么假设我们用力且巧妙的一拍打，恰好可以把所有腰果跳出桌面，停在空中，那么我们用力且巧妙的一拍打就可以理解为是核函数。
所以在非线性 SVM 中，核函数的选择就是影响 SVM 最大的变量。最常用的核函数有线性核、多项式核、高斯核、拉普拉斯核、sigmoid 核，或者是这些核函数的组合。这些函数的区别在于映射方式的不同。通过这些核函数，我们就可以把样本空间投射到新的高维空间中。
常用的核函数为：
3 SKlearn中使用SVM
3.1 SVM的api介绍
from sklearn import svm
# 分类
svm.SVC # 都可以。控制核函数
svm.LinearSVC # 只针对线性核函数
# 回归
svm.SVR
svm.LinearSVR
from sklearn import svm
svm.SVC(
C=1.0,
kernel='rbf',
gamma='scale'
)
- kernel：选择的核函数
- linear：线性核函数
- 线性核函数，是在数据线性可分的情况下使用的， 运算速度快，效果好。不足在于它不能处理线性不可分的数据。
- poly：多项式核函数
- 多项式核函数可以将数据从低维空间映射到高维空间，但参数比较多，计算量大。
- rbf：高斯核函数（默认）
- 高斯核函数同样可以将样本映射到高维空间， 但相比于多项式核函数来说所需的参数比较少，通常性能不错，所以是默认使用的核函数。
- sigmoid：sigmoid 核函数
- 了解深度学习的同学应该知道 sigmoid 经常用在神经网络的映射中。 因此当选用 sigmoid 核函数时，SVM 实现的是多层神经网络。
- C：代表目标函数的惩罚系数，默认为1.0，也就是正则化，也就是软间隔的调整
- 当C越大时，分类器的准确性越高，所以容错率越低，泛化能力就变差。
- 当C越小时，分类器的准确性降低，但容错率增大，泛化能力越强
- gamma：和函数系数，默认为样本特征的倒数。1/n_features
3.2 利用SVM进行乳腺癌检测
from sklearn import svm
import numpy as np
import pandas as pd
- 数据描述
"""
得出信息
- 569条样本数据
- 字段：32个
- 目标(标签)：diagnosis
- B
- M
- 特征：除了标签以外的字段
- id对分类毫无意义：去除
- 其它30个字段：mean,se,worst 分为三组
"""
df = pd.read_csv("svm_data.csv")
df.info()
df.head()
2. 数据处理
- B良性-->0
- M恶性-->1
B映射为0
M映射为1
"""
df["diagnosis"] = df["diagnosis"].map({"M":1,"B":0})
df
"""
id无用，删除
"""
df = df.drop("id",axis=1)
df
"""
特征字段分为三组
- _mean(特征均值)为一组
- _se（特征标准差）为一组
- _worst（特征最差值）为一组
实现：[radius_mean,texture_mean...]
"""
features_mean = df.loc[:,"radius_mean":"fractal_dimension_mean"].columns.tolist()
features_se = df.loc[:,"radius_se":"fractal_dimension_se"].columns.tolist()
features_worst = df.loc[:,"radius_worst":"fractal_dimension_worst"].columns.tolist()
print(features_mean,features_se,features_worst,sep="\n")
- 特征筛选
"""
特征筛选原因：
30个特征很容易过拟合
训练时间消耗过长
"""
import seaborn as sns
from matplotlib import pyplot as plt
# 观察样本集 良性:0 与 恶性:1 数量情况
sns.countplot(df["diagnosis"])
plt.show()
"""
筛选特征-->降维
- 选择mean这组特征。在mean这组特征里面每个特征都一定需要嘛？
- 观察mean这组特征里面两两特征之间的相关性
- 相关程度非常高：选择其中一个作为代表即可
"""
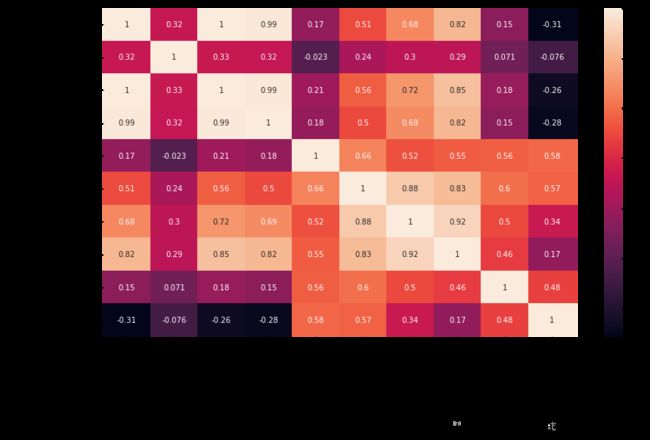
mean_corr = df[features_mean].corr()
mean_corr
"""
来进行相关性的可视化
- 热力图：颜色越浅说明相关程度越大
- annot=True-->显示每个方格的数据
"""
plt.figure(figsize=(14,8))
sns.heatmap(mean_corr,annot=True)
plt.show()
"""
在此处：
得出来radius perimeter area 之间的相关程度很高。任意一个代表
得出来compatctness,concavity,concave_points 之间的相关程度很高。任意一个代表
"""
# 注意 在这个里面里面我们只拿了平均值的特征组，并且去掉一些相关性很大的特征，选择了代表性特征，如下
features_remain = ['radius_mean',
'texture_mean',
'smoothness_mean',
'compactness_mean',
'symmetry_mean',
'fractal_dimension_mean']
- 数据分割
"""
4 数据分割
"""
from sklearn.model_selection import train_test_split
train,test = train_test_split(df,test_size=0.3)
# 构建训练集 测试集 特征数组
train_X = train[features_remain]
test_X = test[features_remain]
# 构建 标签
train_y = train["diagnosis"]
test_y = test["diagnosis"]
- 数据归一化
"""
5 数据归一化
"""
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
train_X = ss.fit_transform(train_X)
test_X = ss.fit_transform(test_X)
- 模型训练及预测
"""
6 模型训练及预测
"""
from sklearn.svm import SVC
model = SVC()
model.fit(train_X,train_y)
predictions = model.predict(test_X)
predictions
- 模型评价
"""
7 模型评价
"""
from sklearn.metrics import accuracy_score
accuracy_score(test_y,predictions) # 0.9298245614035088
整体来说，效果相比我们之前的分类模型，效果可以说是很不错滴，另外也可以选择其他特征组，或者三个特征组一起加入~