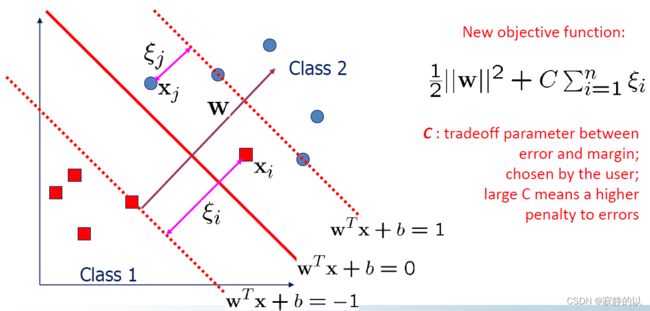
【SVM】简单介绍(四)
1、Soft Margin SVM 对偶求解
构造拉格朗日函数
L = 1 2 ∥ w ∥ 2 + C ∑ i = 1 n ξ i − ∑ i = 1 n α i ( y i ( w T x i + b ) − 1 + ξ i ) − ∑ i = 1 n γ i ξ i α i ≥ 0 γ i ≥ 0 \begin{aligned} & L=\frac{1}{2}\|w\|^2+C \sum_{i=1}^n \xi_i-\sum_{i=1}^n \alpha_i\left(y_i\left(w^T x_i+b\right)-1+\xi_i\right)-\sum_{i=1}^n \gamma_i \xi_i \\ & \alpha_i \geq 0 \quad \gamma_i \geq 0 \end{aligned} L=21∥w∥2+Ci=1∑nξi−i=1∑nαi(yi(wTxi+b)−1+ξi)−i=1∑nγiξiαi≥0γi≥0
求偏导
∂ L ∂ w = 0 ⇒ w = ∑ i α i y i x i ∂ L ∂ b = 0 ⇒ ∑ i α i y i = 0 ∂ L ∂ ξ i = 0 ⇒ α i + γ i = C ⇒ 0 ≤ α i ≤ C \begin{gathered} \frac{\partial L}{\partial w}=0 \Rightarrow w=\sum_i \alpha_i y_i x_i \\ \frac{\partial L}{\partial b}=0 \Rightarrow \sum_i \alpha_i y_i=0 \\ \frac{\partial L}{\partial \xi_i}=0 \Rightarrow \alpha_i+\gamma_i=C \Rightarrow 0 \leq \alpha_i \leq C \end{gathered} ∂w∂L=0⇒w=i∑αiyixi∂b∂L=0⇒i∑αiyi=0∂ξi∂L=0⇒αi+γi=C⇒0≤αi≤C
于是问题转化为
max . W ( α ) = ∑ i = 1 n α i − 1 2 ∑ i = 1 , j = 1 n α i α j y i y j x i T x j subject to C ≥ α i ≥ 0 , ∑ i = 1 n α i y i = 0 \begin{aligned} & \max . W(\boldsymbol{\alpha})=\sum_{i=1}^n \alpha_i-\frac{1}{2} \sum_{i=1, j=1}^n \alpha_i \alpha_j y_i y_j \mathbf{x}_i^T \mathbf{x}_j \\ & \text { subject to } C \geq \alpha_i \geq 0, \sum_{i=1}^n \alpha_i y_i=0 \end{aligned} max.W(α)=i=1∑nαi−21i=1,j=1∑nαiαjyiyjxiTxj subject to C≥αi≥0,i=1∑nαiyi=0
并且注意到 w = ∑ j = 1 s α t j y t j x t j \mathbf{w}=\sum_{j=1}^s \alpha_{t_j} y_{t_j} \mathbf{x}_{t_j} w=∑j=1sαtjytjxtj
- 在对偶空间中,Hard Margin SVM和Soft Margin SVM得到了统一,唯一不同就是这边的拉格朗日乘子 α i \alpha_i αi有一个上界 C C C
- 在对偶空间中,Soft Margin SVM也是一个QP问题!!!
KKT条件
{ α i ( y i f ( x i ) − 1 + ξ i ) = 0 γ i ξ i = 0 α i + γ i = C ⇒ 0 ≤ α i ≤ C \left\{\begin{array}{l} \alpha_i\left(y_i f\left(x_i\right)-1+\xi_i\right)=0 \\ \gamma_i \xi_i=0 \\ \alpha_i+\gamma_i=C \Rightarrow 0 \leq \alpha_i \leq C \end{array}\right. ⎩ ⎨ ⎧αi(yif(xi)−1+ξi)=0γiξi=0αi+γi=C⇒0≤αi≤C
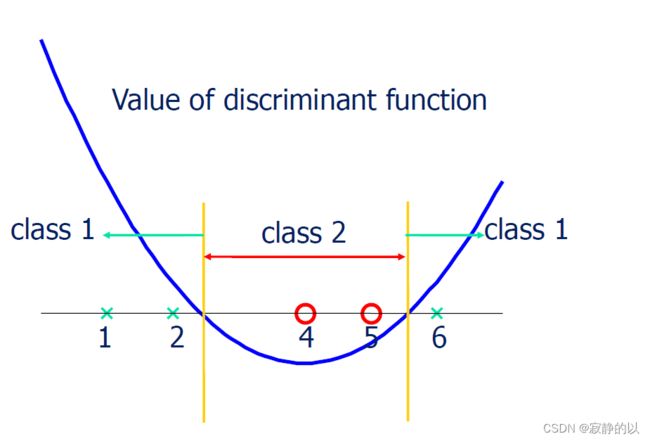
{ α i = 0 ⇒ y i f ( x i ) ≥ 1 ⇒ Samples outside the boundary 0 < α i < C ⇒ y i f ( x i ) = 1 ⇒ Samples on the boundary α i = C ⇒ y i f ( x i ) ≤ 1 ⇒ Samples within the boundary \begin{cases}\alpha_i=0 & \Rightarrow y_i f\left(x_i\right) \geq 1 \Rightarrow \text { Samples outside the boundary } \\ 0<\alpha_i
如何求偏置 b b b
0 < α i < C ⇒ y i f ( x i ) = 1 f ( z ) = ∑ j = 1 s α j y j x j T z + b \begin{gathered} 0<\alpha_i
b = y i − ∑ j = 1 s α j y j x j T x i ∀ 0 < α i < C b=y_i-\sum_{j=1}^s \alpha_j y_j x_j^T x_i \quad \forall 0<\alpha_i
随便找一个支撑向量点,带进去就能算出 b b b。不同的支撑向量点算出的 b b b是一样的。
2、非线性SVM
对于任意给定的线性不可分的数据集,我们总能找到一种映射 ϕ ( ⋅ ) \phi(\cdot) ϕ(⋅),在映射空间中,样本点是线性可分的。
回忆一下
maximize ∑ i = 1 N α i − 1 2 ∑ i = j = 1 N α i α j y i y j x i x j subject to C ≥ α i ≥ 0 , ∑ i = 1 N α i y i = 0 \begin{aligned} \text { maximize } & \sum_{i=1}^N \alpha_i-\frac{1}{2} \sum_{i=j=1}^N \alpha_i \alpha_j y_i y_j x_i x_j \\ \text { subject to } & C \geq \alpha_i \geq 0, \sum_{i=1}^N \alpha_i y_i=0 \end{aligned} maximize subject to i=1∑Nαi−21i=j=1∑NαiαjyiyjxixjC≥αi≥0,i=1∑Nαiyi=0
我们发现,当把数据映射到高维空间后,我们只需要计算数据之间的内积,因此我们不去显式地去定义 ϕ ( ⋅ ) \phi(\cdot) ϕ(⋅),转而去定义高维空间的内积,也就是核函数
K ( x i , x j ) = ϕ ( x i ) ⋅ ϕ ( x j ) K\left(x_i, x_j\right)=\phi\left(x_i\right) \cdot \phi\left(x_j\right) K(xi,xj)=ϕ(xi)⋅ϕ(xj)
所以非线性SVM只要把所有的内积都换成核函数就行了
max . W ( α ) = ∑ i = 1 n α i − 1 2 ∑ i = 1 , j = 1 n α i α j y i y j x i T x j subject to C ≥ α i ≥ 0 , ∑ i = 1 n α i y i = 0 \begin{aligned} & \max . W(\boldsymbol{\alpha})=\sum_{i=1}^n \alpha_i-\frac{1}{2} \sum_{i=1, j=1}^n \alpha_i \alpha_j y_i y_j \mathbf{x}_i^T \mathbf{x}_j \\ & \text { subject to } C \geq \alpha_i \geq 0, \sum_{i=1}^n \alpha_i y_i=0 \end{aligned} max.W(α)=i=1∑nαi−21i=1,j=1∑nαiαjyiyjxiTxj subject to C≥αi≥0,i=1∑nαiyi=0
换成
max . W ( α ) = ∑ i = 1 n α i − 1 2 ∑ i = 1 , j = 1 n α i α j y i y j K ( x i , x j ) subject to C ≥ α i ≥ 0 , ∑ i = 1 n α i y i = 0 \begin{aligned} & \max . W(\boldsymbol{\alpha})=\sum_{i=1}^n \alpha_i-\frac{1}{2} \sum_{i=1, j=1}^n \alpha_i \alpha_j y_i y_j K\left(\mathbf{x}_i, \mathbf{x}_j\right) \\ & \text { subject to } C \geq \alpha_i \geq 0, \sum_{i=1}^n \alpha_i y_i=0 \end{aligned} max.W(α)=i=1∑nαi−21i=1,j=1∑nαiαjyiyjK(xi,xj) subject to C≥αi≥0,i=1∑nαiyi=0
最终的分类器
w = ∑ j = 1 s α t j y t j x t j f = w T z + b = ∑ j = 1 s α t j y t j x t j T z + b \begin{aligned} & \mathbf{w}=\sum_{j=1}^s \alpha_{t_j} y_{t_j} \mathbf{x}_{t_j} \\ & f=\mathbf{w}^T \mathbf{z}+b=\sum_{j=1}^s \alpha_{t_j} y_{t_j} \mathbf{x}_{t_j}^T \mathbf{z}+b \end{aligned} w=j=1∑sαtjytjxtjf=wTz+b=j=1∑sαtjytjxtjTz+b
换成
w = ∑ j = 1 s α t j y t j ϕ ( x t j ) f = ⟨ w , ϕ ( z ) ⟩ + b = ∑ j = 1 s α t j y t j K ( x t j , z ) + b \begin{aligned} \mathbf{w} & =\sum_{j=1}^s \alpha_{t_j} y_{t_j} \phi\left(\mathbf{x}_{t_j}\right) \\ f & =\langle\mathbf{w}, \phi(\mathbf{z})\rangle+b=\sum_{j=1}^s \alpha_{t_j} y_{t_j} K\left(\mathbf{x}_{t_j}, \mathbf{z}\right)+b \end{aligned} wf=j=1∑sαtjytjϕ(xtj)=⟨w,ϕ(z)⟩+b=j=1∑sαtjytjK(xtj,z)+b
可以看到,非线性SVM中,咱们构造不出 w \mathbf{w} w了,好在最终的判别函数要计算的还是内积,可以直接计算判别函数值,而不用去显式地把分类器表示出来。
最终的 b b b
b = y i − ∑ j = 1 s α j y j x j T x i ∀ 0 < α i < C b=y_i-\sum_{j=1}^s \alpha_j y_j x_j^T x_i \quad \forall 0<\alpha_i
换成
b = y i − ∑ j = 1 s α j y j k ( x j , x i ) ∀ 0 < α i < C b=y_i-\sum_{j=1}^s \alpha_j y_j k\left(x_j, x_i\right) \quad \forall 0<\alpha_i
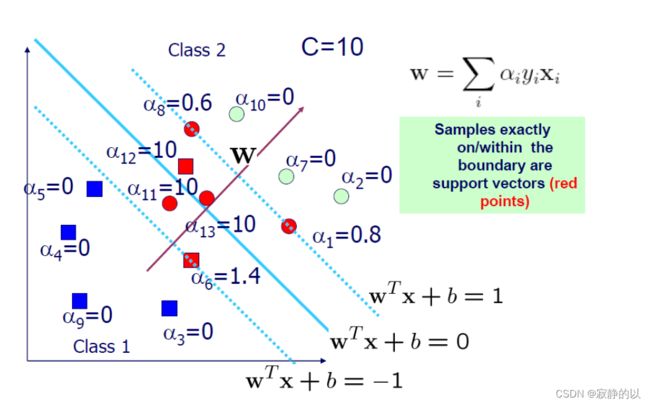
3、An Example
4、SVM是凸优化
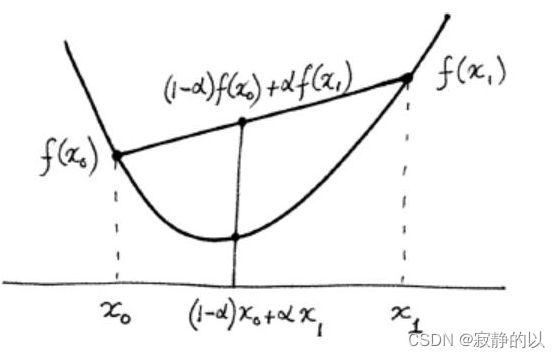
回忆一下凸函数
D − D- D− a domain in R n \mathbb{R}^n Rn
f ( ( 1 − α ) x 0 + α x 1 ) ≤ ( 1 − α ) f ( x 0 ) + α f ( x 1 ) f\left((1-\alpha) \mathbf{x}_0+\alpha \mathbf{x}_1\right) \leq(1-\alpha) f\left(\mathbf{x}_0\right)+\alpha f\left(\mathbf{x}_1\right) f((1−α)x0+αx1)≤(1−α)f(x0)+αf(x1)

SVM的优化问题是
min w ∈ R d C ∑ i N max ( 0 , 1 − y i f ( x i ) ) + ∥ w ∥ 2 \min _{\mathbf{w} \in \mathbb{R}^d} C \sum_i^N \max \left(0,1-y_i f\left(\mathbf{x}_i\right)\right)+\|\mathbf{w}\|^2 w∈RdminCi∑Nmax(0,1−yif(xi))+∥w∥2
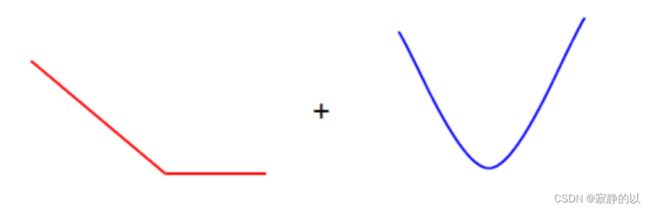
该式左半部分是Hinge Loss的和,右边是一个二次函数,由于凸函数的非负线性组合还是凸函数,所以SVM是个凸优化问题,也就是说,损失函数的 local minimum 就是 global minimum.