论文笔记 An Image Is Worth 16x16 Words: Transformers For Image Recognition At Scale - ICLR 2021
An Image Is Worth 16x16 Words: Transformers For Image Recognition At Scale
ICLR, 2021 PDF | Original Code | Ross Wightman’s Code
1. Network overview
✓ \checkmark ✓ Linear Projection of Flattened Patches
✓ \checkmark ✓ Transformer Encoder
✓ \checkmark ✓ MLP Head
2. Linear Projection of Flattened Patches
The standard Transformer receives as input a 1 D 1\text{D} 1D sequence of token embeddings. To handle 2 D 2\text{D} 2D images, we reshape the image x ∈ R H × W × C {\bf x}\in \mathbb{R} ^{H×W ×C} x∈RH×W×C into a sequence of flattened 2 D 2\text{D} 2D patches x p ∈ R N × ( P 2 ⋅ C ) {\bf x}_p\in \mathbb{R}^{N \times(P^2\cdot C)} xp∈RN×(P2⋅C), where ( H , W ) (H, W ) (H,W) is the resolution of the original image, C C C is the number of channels, ( P , P ) (P, P ) (P,P) is the resolution of each image patch, and N = H W P 2 \displaystyle N=\frac{HW}{P^2} N=P2HW is the resulting number of patches, which also serves as the effective input sequence length for the Transformer. The Transformer uses constant latent vector size D \text{D} D through all of its layers, so we flatten the patches and map to D \text{D} D dimensions with a trainable linear projection . We refer to the output of this projection as the patch embeddings.
Similar to BERT’s [class] token, we prepend a learnable embedding to the sequence of embedded patches ( z 0 0 = x c l a s s {\bf z}_0^0 = {\bf x}_{class} z00=xclass), whose state at the output of the Transformer encoder ( z L 0 ) ({\bf z}_L^0) (zL0)) serves as the image representation y \bf y y . Both during pre-training and fine-tuning, a classification head is attached to. The classification head is implemented by a MLP with one hidden layer at pre-training time and by a single linear layer at fine-tuning time.
z 0 = [ x class ; x p 1 E ; x p 2 E ; ⋯ ; x p N E ] + E pos , E ∈ R ( P 2 ⋅ C ) × D , E p o s ∈ R ( N + 1 ) × D \mathbf{z}_{0} =\left[\mathbf{x}_{\text {class }} ; \mathbf{x}_{p}^{1} \mathbf{E} ; \mathbf{x}_{p}^{2} \mathbf{E} ; \cdots ; \mathbf{x}_{p}^{N} \mathbf{E}\right]+\mathbf{E}_{\text {pos }}, \mathbf{E} \in \mathbb{R}^{\left(P^{2} \cdot C\right) \times D}, \mathbf{E}_{p o s} \in \mathbb{R}^{(N+1) \times D} z0=[xclass ;xp1E;xp2E;⋯;xpNE]+Epos ,E∈R(P2⋅C)×D,Epos∈R(N+1)×D
z ℓ ′ = MSA ( LN ( z ℓ − 1 ) ) + z ℓ − 1 , ℓ = 1 … L \mathbf{z}_{\ell}^{\prime} =\operatorname{MSA}\left(\operatorname{LN}\left(\mathbf{z}_{\ell-1}\right)\right)+\mathbf{z}_{\ell-1}, \ell=1 \ldots L zℓ′=MSA(LN(zℓ−1))+zℓ−1,ℓ=1…L
z ℓ = MLP ( LN ( z ℓ ′ ) ) + z ′ ℓ , ℓ = 1 … L \mathbf{z}_{\ell} =\operatorname{MLP}\left(\operatorname{LN}\left(\mathbf{z}_{\ell}^{\prime}\right)\right)+\mathbf{z}^{\prime} \ell, \ell=1 \ldots L zℓ=MLP(LN(zℓ′))+z′ℓ,ℓ=1…L
y = LN ( z L 0 ) \mathbf{y} =\operatorname{LN}\left(\mathbf{z}_{L}^{0}\right) y=LN(zL0)
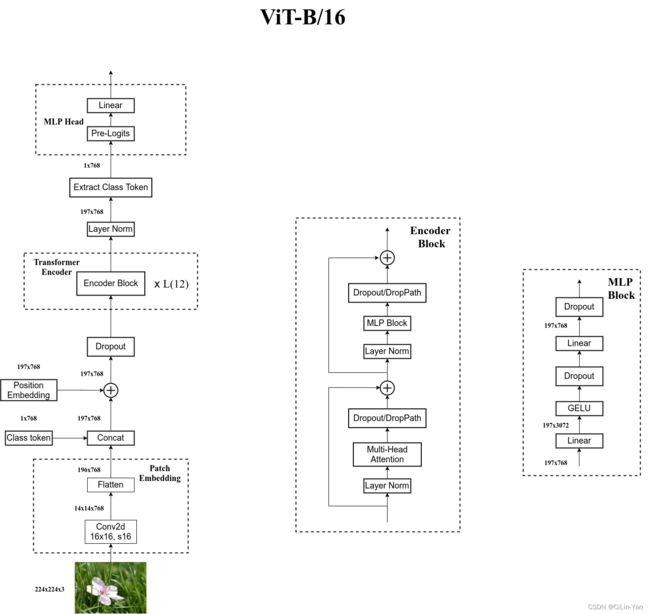
以 ViT-B/16 模型为例,输入图像为[224,224,3], 经过 Linear Project (conv16s16) 得到 [14,14,768] 的 sequence ,Flatten Patches 之后得到 patch embeddings ([196,768]) 。
一个用于 classification 的 token([1,768], learnable embedding) 与patch embeddings ([196,768]) concatenate 得到 [197,768], 之后与 Position Embedding ([197,768]) 相加得到 Transformer Encoder 的输入。
3. Transformer Encoder
3.1 Layer Norm
Layer Normalization 的相关内容可见 这里。
3.2 Multi-Head Attention

-
所谓自注意力机制就是通过某种运算来直接计算得到句子在编码过程中每个位置上的注意力权重;然后再以权重和的形式来计算得到整个句子的隐含向量表示。
-
自注意力机制的缺陷就是:模型在对当前位置的信息进行编码时,会过度的将注意力集中于自身的位置, 因此作者提出了通过多头注意力机制来解决这一问题。
-
多头注意力融合了不同的子空间的表示,多头注意力对同一个单词进行多次映射,每当映射到一个空间时,这个单词就被赋予了新的含义,使得
Transformer注意到子空间的信息。
a. Scaled Dot-Product Attention
The input consists of queries and keys of dimension d k d_{k} dk, and values of dimension d v d_{v} dv. We compute the dot products of the query with all keys, divide each by d k \sqrt{d_{k}} dk, and apply a softmax function to obtain the weights on the values.
In practice, we compute the attention function on a set of queries simultaneously, packed together into a matrix Q Q Q. The keys and values are also packed together into matrices K K K and V V V. We compute the matrix of outputs as:
Attention ( Q , K , V ) = softmax ( Q K T d k ) V \operatorname{Attention}(Q, K, V)=\operatorname{softmax}\left(\frac{Q K^{T}}{\sqrt{d_{k}}}\right) V Attention(Q,K,V)=softmax(dkQKT)V
b. Multi-Head Attention
Multi-head attention allows the model to jointly attend to information from different representation subspaces at different positions. With a single attention head, averaging inhibits this.
MultiHead ( Q , K , V ) = Concat ( head 1 , … , head h ) W O where head = Attention ( Q W i Q , K W i K , V W i V ) \begin{aligned} \operatorname{MultiHead}(Q, K, V) &=\operatorname{Concat}\left(\operatorname{head}_{1}, \ldots, \text { head }_{\mathrm{h}}\right) W^{O} \\ \text { where head } &=\operatorname{Attention}\left(Q W_{i}^{Q}, K W_{i}^{K}, V W_{i}^{V}\right) \end{aligned} MultiHead(Q,K,V) where head =Concat(head1,…, head h)WO=Attention(QWiQ,KWiK,VWiV)
Where the projections are parameter matrices W i Q ∈ R d model × d k , W i K ∈ R d model × d k , W i V ∈ R d model × d v W_{i}^{Q} \in \mathbb{R}^{d_{\text {model }} \times d_{k}}, W_{i}^{K} \in \mathbb{R}^{d_{\text {model }} \times d_{k}}, W_{i}^{V} \in \mathbb{R}^{d_{\text {model }} \times d_{v}} WiQ∈Rdmodel ×dk,WiK∈Rdmodel ×dk,WiV∈Rdmodel ×dv and W O ∈ R h d v × d model W^{O} \in \mathbb{R}^{h d_{v} \times d_{\text {model }}} WO∈Rhdv×dmodel . 此处使用 projection 实现 Q, K, V 的均分,实际使用中也可直接简单切片均分,不使用映射,详细可见:CSDN 博文。
4. MLP Head
以 ViT-B/16 模型为例,Transformer Encoder 输出与输入的 shape 保持不变,既输出的 shape 为 [197,768], 输出经过 Layer Norm 之后直接提取 Class Token ( [1,768] ) 经过 MLP Head 即可得到分类结果。
5. Network Architecture
毕竟是跟着 霹雳吧啦Wz 老师学过来的,附上老师的两张网络结构图 (Bilibili 视频 | CSDN 博文 | Github 地址) 。