二分查找算法详解 + leedcode(162寻找峰值)特殊解法

二分查找常常也会被叫做二分搜索，这个算法思想的时间复杂度为O(log n)。现在谈到时间复杂度可能还有点早，可能有的小伙伴会说时间复杂度还有O(1)呢，这算的了什么？

接下来我们谈几个比较常见的例子：

• 查找数组中等于目标值的索引
• 查找数组中两个数之和等于目标值的索引数组
• 查找数组中目标值最早出现的索引或最晚出现的索引

相信看到以上的一系列问题后，很多小伙伴脑袋里很快会出现for循环遍历的解法，不一会儿就可以解出来，但是一提交发现：超出时间限制！！！

针对这一问题，首先要清楚基本的时间复杂度排序大小：

O(1) < O(log n) < O(n) < O(nlog n) < O(n^2)

了解完这个之后，肯定能看出问题出现在哪儿了吧！！！

接下来我们就展开二分查找的分析吧，来尽量缩小时间的限制。

        能够使用二分查找这一算法思想的前提是：数组是有序的。那无序的怎么办呢，不要着急，后面会列出特殊情况。

一、最基本的二分查找算法

//查找数组中等于目标值target的索引
public int binarySearch(int[] nums, int target) {
    int left = 0;
	int right = nums.length-1;
	while(left <= right) {    //注意条件
		int mid = left + (right - left)/2;
		if(nums[mid] < target) {
			left = mid + 1;   //注意
		} else if(nums[mid] > target) {
			right = mid - 1;  //注意
		} else if(nums[mid] == target) {
			return mid;
		}
	}
	return -1;  //注意
}

基本思想：定义两个指针left、right，根据两个指针找出数组的中间值，在while循环中不断改变left、right、mid这三个值，直至查找到目标值target。

需注意点：while循环条件中 left<=right 与 left

public int binarySearch(int[] nums, int target) {
    int left = 0;
	int right = nums.length-1;
	while(left < right) {    //条件改变
		int mid = left + (right - left)/2;
		if(nums[mid] < target) {
			left = mid + 1;
		} else if(nums[mid] > target) {
			right = mid;  //注意（这里为变成right=mid，因为右边为开区间）
		} else if(nums[mid] == target) {
			return mid;
		}
	}
	return -1;
}

此算法有什么缺陷呢？guess guess(...)  比如一个有序数组 nums = [1,2,2,2,3]，target=2时，该返回哪个索引呢？此时数组中索引 1，2，3 都为2，这就涉及到左右边界问题了。

二、寻找左侧边界的二分查找

//寻找数组中目标值的左侧边界
public int binarySearch(int[] nums, int target) {
    int left = 0;
	int right = nums.length-1;
	while(left <= right) {    
		int mid = left + (right - left)/2;
		if(nums[mid] < target) {
			left = mid + 1;  
		} else if(nums[mid] > target) {
			right = mid - 1;  
		} else if(nums[mid] == target) {
			return mid;
		}
	}
    if(left >= nums.length || nums[left] != target) { //注意
        return -1;
    }
	return left;  //注意
}

分析上述代码点：

1. return -1的条件：退出while循环的条件是 left=right+1，第一种可能是当目标值大于数组中的所有数时，right不需要改变，循环结束后left一定会超出原数组的长度，此时一定不存在；另一种可能是数组中根本没有等于target的索引值。
2. return left 的原因：因为找的是左边界，right会一直向左收缩，当收缩到目标值前一位时停止（left=right+1退出的条件），所以也可以返回 right+1。

三、寻找右侧边界的二分查找

//寻找数组中目标值的右侧边界
public int binarySearch(int[] nums, int target) {
    int left = 0;
	int right = nums.length-1;
	while(left <= right) {    
		int mid = left + (right - left)/2;
		if(nums[mid] < target) {
			left = mid + 1;  
		} else if(nums[mid] > target) {
			right = mid - 1;  
		} else if(nums[mid] == target) {
			return mid;
		}
	}
    if(right < 0 || nums[right] != target) { //注意
        return -1;
    }
	return right;  //注意
}

分析上述代码点：

1. return -1的条件：退出while循环的条件是 left=right+1，第一种可能是当目标值小于数组中的所有数时，left不需要改变，循环结束后right一定不会在数组里面，此时一定不存在；另一种可能是数组中根本没有等于target的索引值。
2. return right的原因：因为找的是右边界，left会一直向右移动，当移动到目标值后一位时停止（left=right+1退出的条件），所以也可以返回 left-1。

特例：

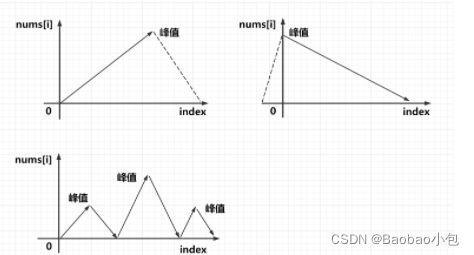
前面说到二分查找针对的是有序数组，那么有特例的数组可以使用这一算法吗？当然有了，比如leedcode上的一道算法题：P162.寻找峰值

这道题中有几个重要的点：

1. nums[-1] = nums[n] = -∞
2. 返回任意一个峰值即可
3. 提示中有提到 “ 对于所有有效的 i 都有nums[i] != nums[i+1] ”

用图表示：

 上代码：

public int findPeakElement(int[] nums) {
        int left = 0, right = nums.length - 1;
        while (left < right) {   //注意
            int mid = left + (right - left) / 2;
            if (nums[mid] > nums[mid + 1]) {
                right = mid;
            } else {
                left = mid + 1;
            }
        }
        return right;
    }

解题思路：由于“ 对于所有有效的 i 都有nums[i] != nums[i+1] ”，即不会出现平的情况，只会出现上坡或者下坡的情况。（当 nums[mid] > nums[mid + 1] 为下坡，所以right向左收缩，峰值在左边；当 nums[mid] < nums[mid + 1] 为上坡，所以left向右移动，峰值在右边）