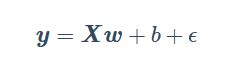[Pytorch]<动手学深度学习>pytorch笔记-----线性回归
1.房屋价格预测的模型建立
1.1数学定义
设房屋的面积为![]() ,房龄为
,房龄为![]() ,售出价格为 y。我们需要建立基于输入
,售出价格为 y。我们需要建立基于输入 ![]() 和
和 ![]() 来计算输出 y 的表达式,也就是模型(model)。顾名思义,线性回归假设输出与各个输入之间是线性关系:
来计算输出 y 的表达式,也就是模型(model)。顾名思义,线性回归假设输出与各个输入之间是线性关系: ![]()
其中 ![]() 和
和 ![]() 是权重(weight),b 是偏差(bias),且均为标量。它们是线性回归模型的参数(parameter)。模型输出
是权重(weight),b 是偏差(bias),且均为标量。它们是线性回归模型的参数(parameter)。模型输出 ![]() 是线性回归对真实价格 y 的预测或估计。我们通常允许它们之间有一定误差。
是线性回归对真实价格 y 的预测或估计。我们通常允许它们之间有一定误差。
1.2模型训练
我们通常收集一系列的真实数据,例如多栋房屋的真实售出价格和它们对应的面积和房龄,作为输入x,我们希望在这个数据上面寻找模型参数来使模型的预测价格与真实价格的误差最小。在机器学习术语里,该数据集被称为训练数据集(training data set)或训练集(training set),一栋房屋被称为一个样本(sample),其真实售出价格(y)叫作标签(label),用来预测标签的两个因素叫作特征(feature)。特征用来表征样本的特点。
假设我们采集的样本数为n,索引为i的样本的特征为![]() 和
和![]() ,标签为
,标签为![]() 。对于索引为 i 的房屋,线性回归模型的房屋价格预测表达式为
。对于索引为 i 的房屋,线性回归模型的房屋价格预测表达式为
![]()
在模型训练中,我们需要衡量价格预测值与真实值之间的误差。通常我们会选取一个非负数作为误差,且数值越小表示误差越小。一个常用的选择是平方函数。它在评估索引为 ii 的样本误差的表达式为
常数项1/2的存在是为了平衡求导后系数为1,误差越小表示预测价格与真实价格越相近,且当二者相等时误差为0。给定训练数据集,这个误差只与模型参数相关,因此我们将它记为以模型参数为参数的函数。在机器学习里,将衡量误差的函数称为损失函数。这里使用的平方误差函数也称为均方误差。
我们用训练数据集中所有样本误差的平均来衡量模型预测的质量,即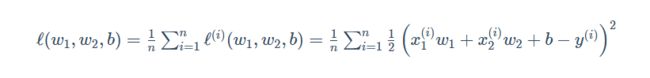
在模型训练中,我们希望找出一组模型参数,来使训练样本平均损失最小:
当模型和损失函数形式较为简单时,上面的误差最小化问题的解可以直接用公式表达出来。这类解叫作解析解(analytical solution),大多数深度学习模型并没有解析解,只能通过优化算法有限次迭代模型参数来尽可能降低损失函数的值。这类解叫作数值解(numerical solution)。
在求数值解的优化算法中,小批量随机梯度下降(miniSGD)在深度学习中被广泛使用。算法:先选取一组模型参数的初始值,如随机选取;接下来对参数进行多次迭代,使每次迭代都可能降低损失函数的值。在每次迭代中,先随机均匀采样一个由固定数目训练数据样本所组成的小批量(mini-batch)![]() ,然后求小批量中数据样本的平均损失有关模型参数的导数(梯度),最后用此结果与预先设定的一个正数的乘积作为模型参数在本次迭代的减小量。
,然后求小批量中数据样本的平均损失有关模型参数的导数(梯度),最后用此结果与预先设定的一个正数的乘积作为模型参数在本次迭代的减小量。
模型的每个参数将作如下迭代:
在上式中,![]() 代表每个小批量中的样本个数(批量大小,batch size),
代表每个小批量中的样本个数(批量大小,batch size),![]() 称作学习率(learning rate)并取正数。需要强调的是,这里的批量大小和学习率的值是人为设定的,并不是通过模型训练学出的,因此叫作超参数(hyperparameter)。我们通常所说的“调参”指的正是调节超参数,例如通过反复试错来找到超参数合适的值。
称作学习率(learning rate)并取正数。需要强调的是,这里的批量大小和学习率的值是人为设定的,并不是通过模型训练学出的,因此叫作超参数(hyperparameter)。我们通常所说的“调参”指的正是调节超参数,例如通过反复试错来找到超参数合适的值。
模型训练完成后,我们将模型参数在优化算法停止时的值分别记作 ![]() 。注意,这里我们得到的并不一定是最小化损失函数的最优解,而是对最优解的一个近似。然后,我们就可以使用学出的线性回归模型来估算训练数据集以外任意一栋面积(平方米)、房龄(年)的房屋的价格了。
。注意,这里我们得到的并不一定是最小化损失函数的最优解,而是对最优解的一个近似。然后,我们就可以使用学出的线性回归模型来估算训练数据集以外任意一栋面积(平方米)、房龄(年)的房屋的价格了。
1.3代码训练
设训练数据集样本数为1000,输入个数(特征数)为2。给定随机生成的批量样本特征,我们使用线性回归模型真实权重![]() 和偏差 b=4.2,以及一个随机噪声项
和偏差 b=4.2,以及一个随机噪声项 ![]() 来生成标签
来生成标签
import torch
import sys
sys.path.append("..")
from d2lzh_pytorch import *
num_inputs = 2 # 输入数为2
num_examples = 1000 # 随机生成的样本数量为1000
true_w = [2, -3.4] # w1=2 w2=-3.4
true_b = 4.2 # b=4.2
features = torch.randn(num_examples, num_inputs,
dtype=torch.float32) # 生成一个2,1000的矩阵 数据类型为float32
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b # w1*1000个随机数(第0行全部元素)+w2*1000个随机数(第1行全部元素)+b
labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()), # 加上一个均值为0 标准差为0.01的正态分布噪声
dtype=torch.float32)
set_figsize()
plt.scatter(features[:, 1].numpy(), labels.numpy(), 1) # 绘制散点图
plt.show()
batch_size = 10
for X, y in data_iter(batch_size, features, labels):
print(X, y)
break
w = torch.tensor(np.random.normal(0, 0.01, (num_inputs, 1)),
dtype=torch.float32) # 把初始权重w进行初始化 生成一个均值为0 标准差为0.01的正态分布,输出一个大小为num_inputs,1的矩阵
b = torch.zeros(1, dtype=torch.float32) # 把初始偏置b初始化为0
w.requires_grad_(True)
b.requires_grad_(True)
lr = 0.03 # 学习率
num_epochs = 3 # 训练次数
net = linreg # 已定义的矩阵乘法 torch.mm(X, w) + b
loss = squared_loss # 使用平方误差
for epoch in range(num_epochs): # 训练模型一共需要num_epochs个迭代周期
# 在每一个迭代周期中,会使用训练数据集中所有样本一次(假设样本数能够被批量大小整除)。
# X和y分别是小批量样本的特征和标签
for X, y in data_iter(batch_size, features, labels):
l = loss(net(X, w, b), y).sum() # l是有关小批量X和y的损失 对矩阵X(影响因素) w(权重)进行相乘 加上偏置b 计算与原数据的均方误差 并加和
l.backward() # 小批量的损失对模型参数求梯度
sgd([w, b], lr, batch_size) # 使用小批量随机梯度下降迭代模型参数
# 不要忘了梯度清零
w.grad.data.zero_()
b.grad.data.zero_()
train_l = loss(net(features, w, b), labels)
print('epoch %d, loss %f' % (epoch + 1, train_l.mean().item()))
print(true_w, '\n', w)
print(true_b, '\n', b)使用nn网络完成训练代码如下:
import torch
from torch.nn import init
import torch.optim as optim
from d2lzh_pytorch import *
import torch.utils.data as Data
num_inputs = 2
num_examples = 1000
true_w = [2, -3.4]
true_b = 4.2
features = torch.tensor(np.random.normal(0, 1, (num_examples, num_inputs)), dtype=torch.float)
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()), dtype=torch.float)
batch_size = 10
# 将训练数据的特征和标签组合
dataset = Data.TensorDataset(features, labels)
# 随机读取小批量
data_iter = Data.DataLoader(dataset, batch_size, shuffle=True) # shuffle=True表示将数据打乱
# 构建网络 使用Sequential 加入一个线性层 输入为num_inputs 输出为1
net = nn.Sequential(
nn.Linear(num_inputs, 1)
# 此处还可以传入其他层
)
init.normal_(net[0].weight, mean=0, std=0.01) # 初始化权重w
init.constant_(net[0].bias, val=0) # 初始化偏置b 也可以直接修改bias的data: net[0].bias.data.fill_(0)
loss = nn.MSELoss() # 设置损失函数为均方损失
optimizer = optim.SGD(net.parameters(), lr=0.03)
num_epochs = 3
for epoch in range(1, num_epochs + 1):
for X, y in data_iter:
output = net(X)
l = loss(output, y.view(-1, 1))
optimizer.zero_grad() # 梯度清零,等价于net.zero_grad()
l.backward() # 小批量的损失对模型参数求梯度
optimizer.step() # 更新参数
print('epoch %d, loss: %f' % (epoch, l.item()))
dense = net[0]
print(true_w, dense.weight)
print(true_b, dense.bias)

![[Pytorch]<动手学深度学习>pytorch笔记-----线性回归_第1张图片](http://img.e-com-net.com/image/info8/c34786092dc245dfbc7ac73cfa2a78a3.jpg)