Pytorch学习笔记---自动求导机制,线性回归模型搭建

一、自动求导机制
torch框架可以自动进行求导，这在搭建网络过程中提供了很大的便利。需要求导的话就在创建tensor时，将求导参数设置为True

import torch
import numpy as np

x = torch.randn(5, 5, requires_grad=True)

这个参数默认为False，因此需要求导时，就将其设置为True。
利用这个机制进行求导：

import torch
import numpy as np
x = torch.randn(5, 5, requires_grad=True)
w = torch.randn(5, 5, requires_grad=True)
c = x*w
a = c.sum()
a.backward()
print(x.grad, w.grad)

上面的流程其实就是神经网络常见的 表达式：
$$F=w\ast x+b$$
在这里b = 0。根据链式求导法则容易得到，对于上述式子，x的梯度就是w, 同样的w的梯度就是x。
在反向梯度传播时，torch会保留上一次运算得到的梯度，并且将梯度进行一次累加操作：

import torch
import numpy as np
x = torch.randn(5, 5, requires_grad=True)
y = torch.randn(5, 5, requires_grad=True)
c = x*y
b = torch.randn(1, requires_grad=True)
a = c.sum() + b
# 求十次梯度， b的梯度累加为10
for i in range(10):
    a.backward(retain_graph=True)
print(b.grad)

二、搭建线性回归模型
线性回归就是一个不加激活函数的全连接层
代码：

import torch
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt
def test():
    x = torch.randn(5, 5, requires_grad=True)
    y = torch.randn(5, 5, requires_grad=True)
    c = x*y
    b = torch.randn(1, requires_grad=True)
    a = c.sum() + b
    for i in range(10):
        a.backward(retain_graph=True)
    print(b.grad)


def linear_regress_data():
    """
    torch搭建线性回归模型
    :return:
    """
    x_train = np.linspace(0, 11, 11, dtype=np.float32).reshape(-1, 1)
    y_values = [2*i + 1 for i in range(11)]
    y_train = np.array(y_values, dtype=np.float32).reshape(-1, 1)
    # print(x_train, '\n', y_train)
    # 将numpy数据类型转换为tensor类型,方便后续训练
    # print(type(x_train))
    x_train = torch.from_numpy(x_train)
    y_train = torch.from_numpy(y_train)
    # print(type(x_train))
    return x_train, y_train


class LinearRegressionModel(nn.Module):
    def __init__(self, input_dim, output_dim):
        super(LinearRegressionModel, self).__init__()
        # 从框架调用网络框架函数
        self.linear = nn.Linear(input_dim, output_dim)

    def forward(self, x):
        out = self.linear(x)
        return out


if __name__ == '__main__':
    model = LinearRegressionModel(input_dim=1, output_dim=1)
    loss_list = []
    # 准备线性拟合数据
    x_train, y_train = linear_regress_data()
    # 设置参数、损失函数
    epochs = 1000
    # 学习率
    learning_rate = 0.01
    # 优化器
    optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate)
    # 损失函数（判别器）
    criterion = nn.MSELoss()
    # 开始训练
    for epoch in range(epochs):
        epoch += 1
        # 每一次迭代都要梯度清零
        optimizer.zero_grad()
        # 前向传播
        outputs = model(x_train)
        # 计算损失函数
        loss = criterion(outputs, y_train)
        # 根据损失进行反向梯度传播
        loss.backward()
        # 更新权重参数
        optimizer.step()
        # 显示迭代的损失
        if epoch % 50 == 0:
            print('epoch :{}, loss :{}'.format(epoch, loss.item()))
            loss_list.append(loss.item())
    # 转换为numpy类型方便绘图
    predict = torch.detach(outputs).numpy()
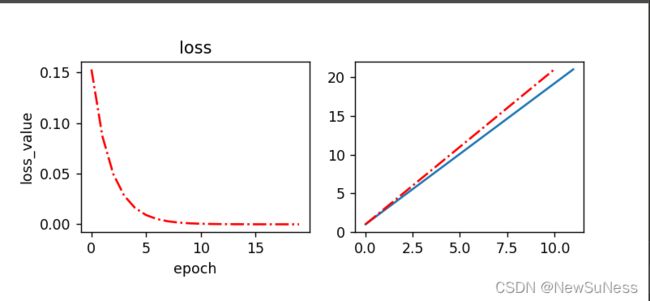
    # 绘制损失函数曲线
    plt.subplot(221)
    plt.plot(loss_list, 'r-.')
    plt.title('loss')
    plt.xlabel('epoch')
    plt.ylabel('loss_value')
    plt.subplot(222)
    plt.plot(x_train, y_train)
    plt.plot(predict,'r-.')
    plt.show()
    # 保存模型,包括权重，偏置参数
    torch.save(model.state_dict(), 'model.pkl')
    # 读取模型
    model.load_state_dict(torch.load('model.pkl'))

实验效果：