【pytorch】1.4 tensor.view()、tensor.reshape()、tensor.resize_() 三者的区别

1、Tensor 内部存储结构

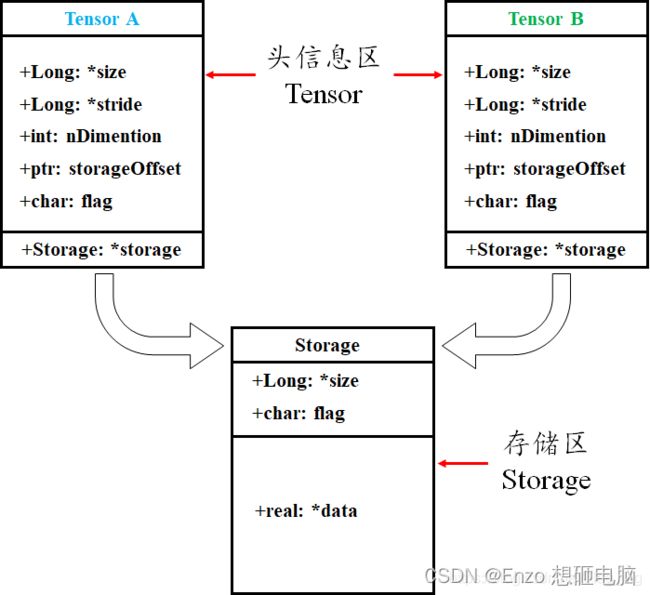
tensor 数据结构如下图所示，tensor 分为头信息区（Tensor）和存储区 （Storage），信息区主要保存着 Tensor 的形状（size）、步长（stride）、数据类型（type ）等信息，而真正的数据则保存成连续的数组，存在存储区。

信息区占用内存较少，主要内存占用取决于 tensor 中元素数目，即存储区大小。由于数据动辄成千数万，所以采取这样的存储方式。

1. 1 tensor 的步长属性: stride()

2.2.1 stride()
在指定维度 dim 上，从一个元素跳到下一个元素所必须的步长（在存储区中经过的元素的个数）

a = torch.randn(3, 2)
print(a.stride())
>>(2, 1)

在第 0 维，想要跳到下一个元素，比如从 a[0][0] 到 a[1][0] ，需要经过 2个元素，步长是 2
在第 1 维，想要跳到下一个元素，比如从 a[0][0] 到 a[0][1]， 需要经过 1个元素，步长是 1

1. 2 tensor 的偏移属性：storage_offset()

表示 tensor 的第 0 个元素与真实存储区的第 0 个元素的偏移量

a = torch.tensor([1, 2, 3, 4, 5])
b = a[1:]
c = a[3:]
print(b.storage_offset())
print(c.storage_offset())
>>1
>>3

可见，b的第 0 个元素与 a 的第 0 个元素之间的偏移量是 1，c 与 a 的偏移量是 3

1.3 存储区

一般来说，一个 tensor 有着与之对应的 storage ， storage 是在 data 之上封装的接口。不同 tensor 的头信息一般不同，但却可能使用相同的 storage。

a.storage() ：查看 a 存储的数据内容
id(a)：查看 a 的内存地址，包括头信息区和存储区
id(a.storage)：查看 a 的存储区的内存地址
a.storage().data_ptr()：返回 a 首元素的内存地址

In [25]: a = t.arange(0, 6)
In [26]: a
Out[26]: tensor([0, 1, 2, 3, 4, 5])

In [27]: a.storage()  # 查看a的存储的数据内容
Out[27]: 
 0
 1
 2
 3
 4
 5
[torch.LongStorage of size 6]

In [28]: a.storage_offset()
Out[28]: 0

In [29]: a.storage_type()
Out[29]: torch.LongStorage

In [30]: b = a.view(2,3)

In [31]: b.storage()
Out[31]: 
 0
 1
 2
 3
 4
 5
[torch.LongStorage of size 6]

可以通过 Python 的 id 值来判断它们在内存中的地址是否相等。

In [32]: id(a) == id(b)
Out[32]: False

In [33]: id(a.storage) == id(b.storage)
Out[33]: True

可以看到 a 和 b 的 storage 是相等的。

a 改变，b 也跟着改变，因为它们是共享 storage 的。

In [34]: a[1] = 100

In [35]: b
Out[35]: 
tensor([[  0, 100,   2],
        [  3,   4,   5]])

数据和存储区的差异，c 的数据是切片之后的值，而存储区仍然是整体的值。

In [36]: c = a[2:]

In [37]: c
Out[37]: tensor([2, 3, 4, 5])

In [43]: c.data
Out[43]: tensor([2, 3, 4, 5])

In [38]: c.storage()
Out[38]: 
 0
 100
 2
 3
 4
 5
[torch.LongStorage of size 6]

In [39]: c.data_ptr(), a.data_ptr()
Out[39]: (132078864, 132078848)

In [40]: c.data_ptr() - a.data_ptr()
Out[40]: 16

data_ptr() 返回 tensor 首元素的内存地址，c 和 a 的内存地址相差 16，也就是两个元素，即每个元素占用 8 个字节（LongStorage）。

c[0] 的内存地址对应 a[2] 内存地址。

In [44]: c[0] = -100

In [45]: a
Out[45]: tensor([   0,  100, -100,    3,    4,    5])

a.storage、b.storage 、c.storage 三者的内存地址是相等的。

In [49]: id(a.storage) == id(b.storage) == id(c.storage)
Out[49]: True

In [51]: a.storage_offset(), b.storage_offset(), c.storage_offset()
Out[51]: (0, 0, 2)

查看偏移位。

In [55]: d = b[::2, ::2]

In [56]: d
Out[56]: tensor([[   0, -100]])

In [57]: b
Out[57]: 
tensor([[   0,  100, -100],
        [   3,    4,    5]])

In [58]: id(d.storage) == id(b.storage)
Out[58]: True

In [59]: b.stride()
Out[59]: (3, 1)

In [60]: d.stride()
Out[60]: (6, 2)

In [61]: d.is_contiguous()
Out[61]: False

由此可见，绝大多数操作并不修改 tensor 的数据，只是修改了 tensor 的头信息，这种做法更节省内存，同时提升了处理速度。此外，有些操作会导致 tensor 不连续，这时需要调用 torch.contiguous 方法将其变成连续的数据，该方法会复制数据到新的内存，不在与原来的数据共享 storage。

高级索引一般不共享 storage ，而普通索引共享 storage ，是因为普通索引可以通过修改 tensor 的 offset 、stride 和 size 实现，不修改 storage 的数据，而高级索引则不行。

---

2、tensor的连续性

tensor 的连续性说的其实是 stride() 属性 和 size() 之间的关系

连续性条件：$stride[i]=stride[i+1]\ast size[i+1]$

意思就是，第 $i$ 维跳到下一个元素走的步数，是 $i+1$ 维走到下一维的步数，乘以 $i+1$ 维数的个数。

比如二维数组中 $stride[0]=stride[1]\ast size[1]$ ，代表的就是第 0 维走到下一个数，需要走完这一行。

比如上面的例子中

a = torch.tensor([1, 2, 3, 4, 5, 6])
b = a.view(2, 3)

对 b 来说：stride[0] = 3，stride[1] = 1，size[1] = 3。满足上面的条件

直观来说，就是：在存储区的真实数据中，在我旁边的数，现在还在我旁边，就叫连续

有些操作会改变连续性，比如转置

a = torch.tensor([1, 2, 3, 4, 5, 6]).view(2, 3)
b = a.t()
print(f'a : {a}')
print(f'b : {b}')
print(a.stride())
print(b.stride())
>>a : tensor([[1, 2, 3],
        [4, 5, 6]])
>>b : tensor([[1, 4],
        [2, 5],
        [3, 6]])
>>(3, 1)
>>(1, 3)

b 是 a 的转置。
在第 0 维走到下一个元素，也就是 b[0][0] 走到b[1][0]，从值为1的元素走到值为2 的元素，（在存储区的数据上看）步长是 1， $stride[0]=1$
同理， $stride[1]=3$，$size[1]=3$
这就不满足式子了：$stride[0]=stride[1]\ast size[1]$，因此是不连续的

---

3、tensor.view()、tensor.reshape()、tensor.resize_() 三者的区别

3.1 view()

view 从字面意思上就是 视图 的意思。因此，就是将数据以某种排列方式展示给我们，不改变存储区的真实数据，只改变头信息区

a = torch.tensor([1, 2, 3, 4, 5, 6])
b = a.view(2, 3)
print(f'a : {a}')
print(f'b : {b}')
print(f'storage address of a: {a.storage().data_ptr()}')
print(f'storage address of b: {b.storage().data_ptr()}')
>>a : tensor([1, 2, 3, 4, 5, 6])
>>b : tensor([[1, 2, 3],
              [4, 5, 6]])
>>storage address of a: 93972187307840
>>storage address of b: 93972187307840

以上可见，二者共享存储区

print(f'storage  of a: {a.storage()}')
print(f'storage  of b: {b.storage()}')
>>[torch.LongStorage of size 6]
storage  of a:  
 1
 2
 3
 4
 5
 6
>>[torch.LongStorage of size 6]
storage  of b:  
 1
 2
 3
 4
 5
 6

以上可见，存储区的数据并没有发生改变

print(f'stride of a : {a.stride()}')
print(f'stride of b : {b.stride()}')
>>(1,)
>>(3, 1)

以上可见，stride 发生改变，也就是头信息区发生改变

3.2. reshape()

不连续是不能使用 view() 方法的。那有什么办法可以让不连续的tensor 使用 view() 呢？就是将其连续化（b.contiguous()）

a = torch.tensor([1, 2, 3, 4, 5, 6]).view(2, 3)
b = a.t()
c = b.contiguous()
print(f'a : {a}')
print(f'b : {b}')
print(f'c : {c}')
# a : tensor([[1, 2, 3],
#             [4, 5, 6]])
# b : tensor([[1, 4],
#             [2, 5],
#             [3, 6]])
# c : tensor([[1, 4],
#             [2, 5],
#             [3, 6]])

print(f'stride of a : {a.stride()}')
print(f'stride of b : {b.stride()}')
print(f'stride of c : {c.stride()}')
# tride of a : (3, 1)
# stride of b : (1, 3)
# stride of c : (2, 1)

print(f'storage of a: {a.storage()}')
print(f'storage of b: {b.storage()}')
print(f'storage of c: {c.storage()}')
# storage of a:  1
#  2
#  3
#  4
#  5
#  6
# [torch.storage._TypedStorage(dtype=torch.int64, device=cpu) of size 6]
# storage of b:  1
#  2
#  3
#  4
#  5
#  6
# [torch.storage._TypedStorage(dtype=torch.int64, device=cpu) of size 6]
# storage of c:  1
#  4
#  2
#  5
#  3
#  6
# [torch.storage._TypedStorage(dtype=torch.int64, device=cpu) of size 6]

print(f'storage address of a: {a.storage().data_ptr()}')
print(f'storage address of b: {b.storage().data_ptr()}')
print(f'storage address of c: {c.storage().data_ptr()}')
# storage address of a: 140157418240832
# storage address of b: 140157418240832
# storage address of c: 140157373156288

我们看到，c 的数据恢复了连续性，且其存储区的地址与 a, b 不同了。

contiguous() 函数其实就是创造了一个全新的 tensor。在存储区中，将 b 中的数据按顺序存放，得到 c

了解 contiguous() 之后，我们就来看看 reshape 的特性：

import torch

print('=============== view ===============')
a = torch.tensor([1, 2, 3, 4, 5, 6])
b = a.view(2, 3)
print(f'storage address of a: {a.storage().data_ptr()}')   # storage address of a: 140386136382336
print(f'storage address of b: {b.storage().data_ptr()}')   # storage address of a: 140386136382336

b[0, 1] = 9
print(f'a : {a}')    # a : tensor([1, 9, 3, 4, 5, 6])
print(f'b : {b}')    # b : tensor([[1, 9, 3], [4, 5, 6]])


print('============== 张量x满足连续性时  使用reshape ==============')
x = torch.tensor([1, 2, 3, 4, 5, 6]).view(2, 3)
y = x.reshape(3, 2)

print(f'storage address of x: {x.storage()}')   # storage address of x:  1 2 3 4 5 6
print(f'storage address of y: {y.storage()}')   # storage address of x:  1 2 3 4 5 6

print(f'storage address of x: {x.storage().data_ptr()}')   # storage address of x: 140529895254784
print(f'storage address of y: {y.storage().data_ptr()}')   # storage address of x: 140529895254784

y[0, 1] = 9
print(f'x : {x}')   # x : tensor([[1, 9, 3], [4, 5, 6]])
print(f'y : {y}')   # y : tensor([[1, 9], [3, 4], [5, 6]])


print('============== 张量m不满足连续性时  使用reshape ==============')
m = torch.tensor([1, 2, 3, 4, 5, 6]).view(2, 3).T
n = m.reshape(2, 3)
print(f'storage address of m: {m.storage()}')   # storage address of x:  1 2 3 4 5 6
print(f'storage address of n: {n.storage()}')   # storage address of x:  1 4 2 5 3 6

print(f'storage address of m: {m.storage().data_ptr()}')   # storage address of m: 140529894838912
print(f'storage address of n: {n.storage().data_ptr()}')   # storage address of n: 140529894443968

n[0, 1] = 9
print(f'm : {m}')   # m : tensor([[1, 4], [2, 5], [3, 6]])
print(f'n : {n}')   # n : tensor([[1, 9, 2], [5, 3, 6]])

这样我们可以说明 reshape() 和 view() 的区别了：

• 当 tensor 满足连续性要求时，reshape() = view()，和原来 tensor 共用存储区
• 当 tensor 不满足连续性要求时 (不连续是不能使用 view() 方法的)，reshape() = **contiguous() + view()，会产生新的存储区的 tensor，与原来 tensor 不共用存储区

3.3. resize_()

前面说到的 reshape 和 view 都必须要用到全部的原始数据，比如你的原始数据只有12个，无论你怎么变形都必须要用到12个数字，不能多不能少。因此你就不能把只有12个数字的 tensor 强行 reshap 成 2*5 的维度的tensor。但是 resize_() 可以做到，无论你存储区原始有多少个数字，我都能变成你想要的维度，数字不够怎么办？随机产生凑！数字多了怎么办？就取我需要的部分！

1) 数据多的时候

a = torch.tensor([1, 2, 3, 4, 5, 6, 7])
b = a.resize_(2, 3)
print(f'a : {a}')
print(f'b : {b}')
print(f'stride of a : {a.stride()}')
print(f'stride of b : {b.stride()}')
print(f'storage address of a: {a.storage().data_ptr()}')
print(f'storage address of b: {b.storage().data_ptr()}')
>>a : tensor([[1, 2, 3],
        [4, 5, 6]])
>>b : tensor([[1, 2, 3],
        [4, 5, 6]])
>>stride of a : (3, 1)
>>stride of b : (3, 1)
>>storage address of a: 94579423708416
>>storage address of b: 94579423708416

print(a.storage())
>> 
 1
 2
 3
 4
 5
 6
 7

可见，取的是前 6 个。

会改变 a，但是并没有改变存储区中的数据，a, b 共用存储区

2) 数据少的时候

import torch

a = torch.tensor([1, 2, 3, 4, 5])
print(f'a : {a}')   # a : tensor([1, 2, 3, 4, 5])
print(f'storage address of a: {a.storage().data_ptr()}')  # storage address of a: 140227893580544

b = a.resize_(2, 3)
print(f'a : {a}')  # a : tensor([[1, 2, 3], [4, 5, 140381257865520]])
print(f'b : {b}')  # b : tensor([[1, 2, 3], [4, 5, 140381257865520]])

print(f'stride of a : {a.stride()}')   # stride of a : (3, 1)
print(f'stride of b : {b.stride()}')  # stride of b : (3, 1)
print(f'storage address of a: {a.storage().data_ptr()}')  # storage address of a: 140227838241728
print(f'storage address of b: {b.storage().data_ptr()}')  # storage address of a: 140227838241728

可见，补充了一个数

会改变 a，且改变了存储区中的数据，a, b 共用存储区（但是已经不是刚刚那个存储区了，地址变了）