Matlab插值与拟合

一、插值（二维、三维）

    插值就是在已知数据之间计算估计值的过程，是一种实用的数值方法，是函数逼近的重要方法。在信号处理和图形分析中，插值运算的应用较为广泛，MATLAB提供了多种插值函数，可以满足不同的需求。

①二维

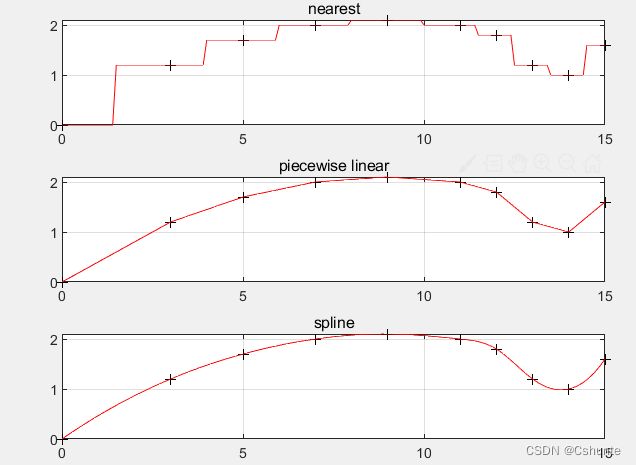
在matlab中自带的一维插值函数有：interp1，其函数定义式如下：

yi = interp1(x,y,xi,'method')

其中method代表插值方法，有：                  （缺省时默认为线性插值）

  1.nearest-----最邻近插值

  2.linear------线性插值

  3.spline-------三次样条插值

  4.cubic--------立方插值

栗子：

clc;clear
x0 = [0 3 5 7 9 11 12 13 14 15];               %离散自变量
y0 = [0 1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.0 1.6];  %离散点对应的值
x = 0:0.1:15;
y2 = interp1(x0,y0,x);                         %缺省为线性插值
y3 = interp1(x0,y0,x,'spline')                 %三次样条插值
subplot(3,1,1);
plot(x0,y0,'k+',x,y1,'r');
grid;
title('lagrange');
subplot(3,1,2);
plot(x0,y0,'k+',x,y2,'r');
grid;
title('piecewise linear');                  
subplot(3,1,3);
plot(x0,y0,' k+',x,y3,'r');
grid;
title( 'spline');

②三维

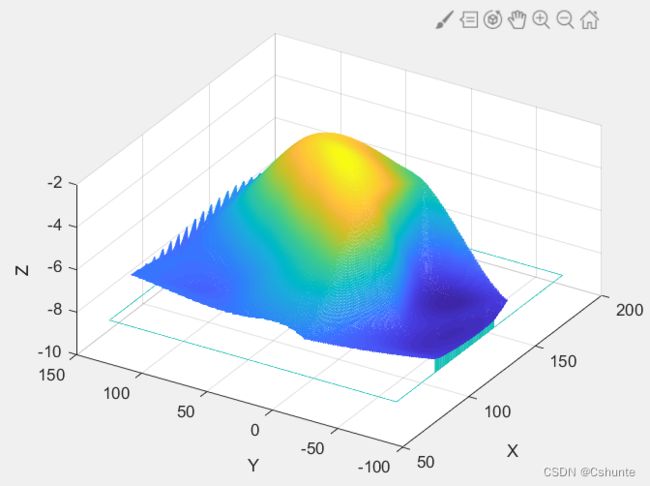
在matlab中自带的一维插值函数有：griddata，其函数定义式如下：

zi=griddata(x,y,z,xi,yi,'method') %x,y和xi,yi通常为向量

插值的方法有：                                                    （缺省时默认为双线性插值）

  1.nearest-----最邻近插值

  2.linear------双线性插值

  3.spline-------双三次样条插值

  4.cubic--------双立方插值

栗子：

clear；clc
x=[129 140 103.5 88 185.5 195 105.5 157.5 107.5 77 81 162 162 117.5];
y=[7.5 141.5 23 147 22.5 137.5 85.5 -6.5 -81 3 56.5 -66.5 84 -33.5];
z=[-4 -8 -6 -8 -6 -8 -8 -9 -9 -8 -8 -9 -4 -9];
[xi,yi]=meshgrid(75:0.5:200,-70:0.5:150);
zi=griddata(x,y,z,xi,yi,'cubic');                   %散乱点插值
figure(1);
meshz(xi,yi,zi);
xlabel('X'),ylabel('Y'),zlabel('Z');

二、拟合

    拟合：拟合是指已知某函数的若干离散函数值,通过调整该函数中若干待定系数，使得该函数与已知点集的方差最小。

①多项式拟合

matlab自带的多项式拟合函数：polyfit函数，其用法如下：

[a,S] = polyfit(x,y,n);   

    x、y是被拟合数据的自变量和因变量  n为拟合多项式的次数  a为拟合多项式系数构成的向量
S为分析拟合效果所需的指标（可省略）

栗子：

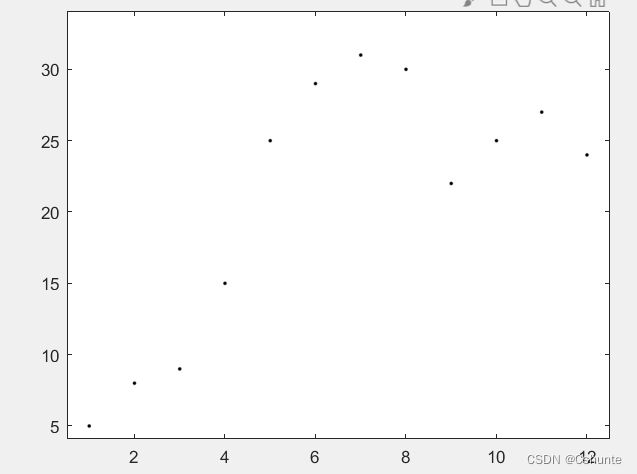
    假设我们现在有一组二维散点，如下所示：

 多次尝试之后，n取值为9的时候拟合效果最好：  （n<=9）

代码如下：

clc;clear
x=1:12;                                
y=[5,8,9,15,25,29,31,30,22,25,27,24];
a=polyfit(x,y,9);
xp=1:0.1:12;
yp=polyval(a,xp);
plot(x,y,'.k',xp,yp);

②指定函数拟合

syms t;
x=[0;0.4;1.2;2;2.8;3.6;4.4;5.2;6;7.2;8;9.2;10.4;11.6;12.4;13.6;14.4;15];
y=[1;0.85;0.29;-0.27;-0.53;-0.4;-0.12;0.17;0.28;0.15;-0.03;-0.15;-0.071;0.059;0.09;0.032;-0.015;-0.02];%指定函数形式为f(t)=acos(kt)e^(wt),进行拟合
f=fittype('a*cos(k*t)*exp(w*t)','independent','t','coefficients',{'a','k','w'});
cfun=fit(x,y,f)     %显示拟合函数
xi=0:.1:20;
yi=cfun(xi);
plot(x,y,'r*',xi,yi,'b-');

其效果如下所示：

结果显示的最佳参数：

    matlab中还有许多自带的插值拟合函数，除本文几个较为基础的函数以外就不多提及了。读者感兴趣的话可以去挖掘。