数值计算与MATLAB微积分

前言

本文主要介绍了数值微分、数值积分的方法，以及MATLAB利用数值微积分方法进行微积分运算的方法。

如果读者只是为了快速了解MATLAB数值运算方法则可直接阅读微、积分运算章节，但为了更加熟练的使用微积分运算，还是建立读者先本文顺序先学习数值微积分的方法。在学习过程可以发现，MATLAB微积分运算章节与数值微积分章节都是一一对应的。

数值微分

导数的差分公式

我们在高等数学中学习过，函数在附近某点取值的近似公式——泰勒公式为：$f(x+h)=f\left(x\right)+h\frac{f^{\prime }\left(x\right)}{1!}+h^2\frac{f^{\prime \prime }(x)}{2!}+\cdots +h^n\frac{f^{(n)}\left(x\right)}{n!}+o\left(h^n\right)$

由泰勒展开式 $f(x+h)=f(x)+h{f}^{\prime }(x)+o(h^2)$，$f(x-h)=f(x)-h{f}^{\prime }(x)+o(h^2)$，得一阶导数的差分公式：

向前差分	向后差分	中心差分
$f^{\prime }(x)=\frac{f(x+h)-f(x)}{h}+o(h)$	$f^{\prime }(x)=\frac{f(x)-f(x-h)}{h}+o(h)$	$f^{\prime }(x)=\frac{f(x+h)-f(x-h)}{2h}+o(h^2)$

无穷小量的阶数代表了算法的精度，当公式形式变为$f^{(k)}x=[]+o(h^n)$时，$o(h^n)$表示公式为n阶精度的差分公式。

一阶的4阶精度的差分公式：$f^{\prime }(x)=\frac{8\left[f(x+h)-f(x-h)\right]-\left[f(x+2h)-f(x-2h)\right]}{12h}+o(h^4)$；

这里前一个阶数指所要表示的 $f^{(n)}$ 的阶数，第二个阶数指公式对应的精度。

二阶的2阶精度的差分公式：$f^{\prime \prime }(x)=\frac{f(x+h)-2f(x)+f(x-h)}{h^2}+o(h^2)$；

三阶的2阶精度的差分公式：$f^{\prime \prime \prime }(x)=\frac{\left[f(x+2h)-f(x-2h)\right]-2\left[f(x+h)-f(x-h)\right]}{2h^3}+o(h^2)$。

偏微分的差分公式

nabla算子的运算

$\nabla f=({\partial }_{x}f,{\partial }_{y}f,\partial f)$， $\nabla \cdot F={\partial }_x{F}_x+{\partial }_y{F}_y+{\partial }_z{F}_z$， ${\nabla }^{2}f=({\partial }_x^2+{\partial }_y^2+{\partial }_z^2)f$。

$\nabla \times F=\left({\partial }_y{F}_z-{\partial }_z{F}_y,{\partial }_z{F}_x-{\partial }_x{F}_z,{\partial }_x{F}_y-{\partial }_y{F}_x\right)$

nabla算子对应的数值差分公式

$$\begin{array}{rl}& \nabla f=\left({\partial }_{x}f,{\partial }_{y}f,{\partial }_{z}f\right)=\left(\frac{f_{i+1,j,k}-f_{i-1,j,k}}{2h},\frac{f_{i,j+1,k}-f_{i,j-1,k}}{2h},\frac{f_{i,j,k+1}-f_{i,j,k-1}}{2h}\right)\\ & {\nabla }^{2}f=\left({\partial }_x^{2}f+{\partial }_y^{2}f+{\partial }_z^{2}f\right)\\ & =\left(\frac{f_{i+1,j,k}+f_{i-1,j,k}-2f_{i,j,k}}{h^2}+\frac{f_{i,j+1,k}+f_{i,j-1,k}-2f_{i,j,k}}{h^2}+\frac{f_{i,j,k+1}+f_{i,j,k-1}-2f_{i,j,k}}{h^2}\right)\\ & \mathbf{F}=(Fx(\mathbf{r}),Fy(\mathbf{r}),Fz(\mathbf{r}));\mathbf{r}=(x,y,z)\\ & \nabla \cdot \mathbf{F}={\partial }_x{F}_x(\mathbf{r})+{\partial }_y{F}_y(\mathbf{r})+{\partial }_z{F}_z(\mathbf{r})\\ & =\frac{F{x}_{i+1,j,k}-F{x}_{i-1,j,k}}{2h}+\frac{F{y}_{i,j+1,k}-F{y}_{i,j+1,k}}{2h}+\frac{F{z}_{i,j,k+1}-F{z}_{i,j,k-1}}{2h}\\ & {\partial }_{y}Fz(\mathbf{r})-{\partial }_{z}Fy(\mathbf{r})=\frac{F{z}_{i,j+1,k}-F{z}_{i,j-1,k}}{2h}-\frac{F{y}_{i,j,k+1}-F{y}_{i,j,k-1}}{2h}\end{array}$$

数值积分

我们先推导数值积分的近似计算公式。

一维定积分 $I={\int }_a^{b}f(x)\mathrm{d}x$ 的几何意义是曲线下面所包围的面积，按照积分的定义，它是许多小曲边梯形面积之和的极限 $I={\int }_a^{b}f(x)\mathrm{d}x={\lim }_{n\to \infty }{\sum }_{k=1}^{n}f\left({\xi }_k\right)\frac{b-a}{n}$。

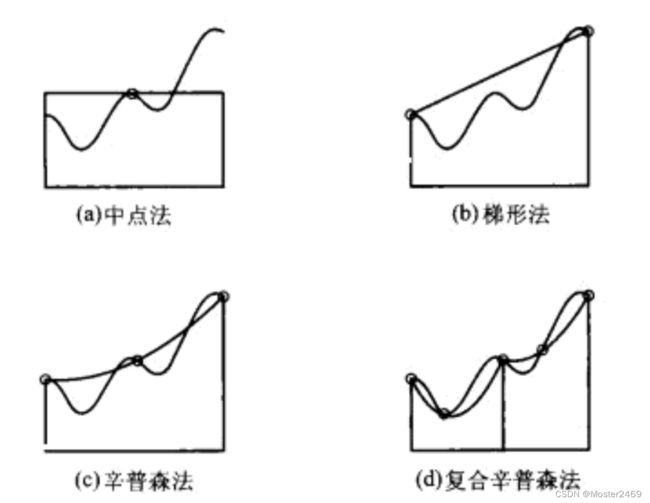
令 $h=\frac{b-a}{n}$，将微分的数值计算过程倒转可得到“向前积分”和“向后积分”公式，它们都叫矩形公式，都是用矩形来替代曲边梯形。$L_n=h{\sum }_{k=0}^{n-1}{f}_k,R_n=h{\sum }_{k=1}^n{f}_k$。

将两式平均得出近似计算定积分的梯形公式：$T_n=h{\sum }_{k=1}^{n-1}{f}_k+\frac{h}{2}\left(f_0+f_n\right)$；

将中心差分的过程倒转得到了中点法(积分)公式：$M_n=h{\sum }_{k=0}^{n-1}f(x_{k+\frac{1}{2}})$。

在高等数学中介绍过，辛普森(Simpson)公式：$S_n=\frac{h}{3}\left(f_0+f_{2n}+2{\sum }_{k=1}^{n-1}{f}_{2k}+4{\sum }_{k=0}^{n-1}{f}_{2k+1}\right)$。

在a,b两点间，辛普森公式为：$S=\frac{h}{6}(f(a)+4f(\frac{a+b}{2})+f(b))$

在a,b区间内，辛普森公式使用了$f(a),f(b)$以及中点$f(\frac{a+b}{2})$，更进一步，还可以再多使用两个点$f(\frac{3a+b}{4})$和$f(\frac{a+3b}{4})$得到复合辛普森公式：$S=\frac{h}{12}(f(a)+4f(\frac{3a+b}{4})+\frac{a+b}{2}+4f(\frac{a+3b}{4})+f(b))$。

对数值积分的方法做个简单整理

矩形公式：$L_n=h{\sum }_{k=0}^{n-1}{f}_k,R_n=h{\sum }_{k=1}^n{f}_k$。

梯形公式：$T_n=h{\sum }_{k=1}^{n-1}{f}_k+\frac{h}{2}\left(f_0+f_n\right)$；

中点法：$M_n=h{\sum }_{k=0}^{n-1}f(x_{k+\frac{1}{2}})$。

在a,b两点间，辛普森公式为：$S=\frac{h}{6}(f(a)+4f(\frac{a+b}{2})+f(b))$

在a,b区间内，复合辛普森公式：$S=\frac{h}{12}(f(a)+4f(\frac{3a+b}{4})+\frac{a+b}{2}+4f(\frac{a+3b}{4})+f(b))$。

六阶牛顿-柯林特法则

牛顿-柯林特法则是在辛普森公式等四阶积分法则上进行的修正。$S$ 和 $S_2$ 是同一个积分的近似值 ($S_2$的步长是$S$的一半)，因此它们之间的差可以用于估计误差 $E=S_2-S$。而且他们还可以结合起来得到一个更准确的近似值$Q$，而由步长和原来积分法则是4阶可知，$S_2$的准确值大约是$S$的$2^4$倍，所以 $Q-S=16(Q-S_2)$，因此 $Q=S_2+(S_2-S)/15$。

数值积分的阶数

数值积分的阶数指使用该法则不能精确计算的多项式的最低次数。

以中点法为例，中点法只能对 $f(x)=Const$ 以及 $f(x)=kx+Const$ 等函数进行精确计算，对于$f(x)=k{x}^2$则无法精确计算，因此中点法阶数为2阶。

类似可得，辛普森和复合辛普森公式阶数为4。

微分运算

微分运算与数值微分的方法相对应，先做个简单的复习。

数值微分的常有方法有向前差分 $f^{\prime }(x)=\frac{f(x+h)-f(x)}{h}+o(h)$、向后差分 $f^{\prime }(x)=\frac{f(x)-f(x-h)}{h}+o(h)$、中心差分 $f^{\prime }(x)=\frac{f(x+h)-f(x-h)}{2h}+o(h^2)$ 与二阶的差分公式：$f^{\prime \prime }(x)=\frac{f(x+h)-2f(x)+f(x-h)}{h^2}+o(h^2)$。

差分运算 diff

%% diff 
% 向量差分
a = [1 4 5 7 8 9];
diff(a)		% 类似于向前差分, ans=[3 1 2 1 1]
diff(a,2)	% diff(a,2)=diff(diff(a)), ans=[-2 1 -1 0]

% 矩阵差分
b = [1 3 4; 4 6 7; 2 1 7];
diff(b)		% 矩阵差分是竖直方向操作的, ans=[3 3 3; -2 -5 0]
diff(b,3)	% diff(b,3)=diff(diff(diff(b))), ans=[-3 5]

梯度运算 gradient

%% gradient
% 向量梯度
a = [1 4 5 7 8 9];
gradient(a)		% 对向量各点取中心差分, 端点处则取向前/向后差分 
% ans = [-3.0000 2.0000 1.5000 1.5000 1.0000 1.0000]

% 矩阵梯度
b = [1 3 4; 4 6 7; 2 1 7];	
gradient(b)		% 矩阵梯度又变为了横向的中心差分操作, 同样在端点处变为横向向前/向后差分
% ans = [2.0000 1.5000 1.0000; 2.0000 1.5000 1.0000 -1.0000 2.5000 6.0000]
[px, py]=gradient(b)	% 若使用两个矩阵承接矩阵梯度的结果, 则除px为gradient(b)的结果外, 还可以得到py为纵向的差分运算的结果。

离散拉普拉斯算符 del2

%% del2
x = [1 2 3 4 5 6 7 8];
fx=x.^2;
4*del2(fx)	% 4*del2相当于f''(需要乘4为del2函数的性质), ans=[2 2 2 2 2 2 2 2]
gx=x.^3;
4*del2(gx)	% ans=[6 12 18 24 30 36 42 48]

不要忘记del2也是数值计算，它在计算二阶导数时必然后对应公式，由于fx,gx阶数较低才可准确计算出导数。del2对应的公式为二阶的精度为2阶的差分公式 $f^{\prime \prime }(x)=\frac{f(x+h)-2f(x)+f(x-h)}{h^2}+o(h^2)$，h默认为1。

一旦del2要处理的函数阶数超过二阶差分公式的精度，那么del2就不可用f’'(x)进行计算。

a = [1 4 5 7 8 9];
4*del2(a)	% ans=[-5 -2 1 -1 0 1]
% 对于左端点 ans(1)=2*a(1)-5*a(2)+4*a(3)-a(4), 右端点同理

% 矩阵拉普拉斯算子
b = [1 3 4; 4 6 7; 2 1 7];	
4*del2(b)	% 对列表del2公式扩展 I(i,j)=[f(i+1,j)+f(i,j+1)+f(i-1,j)+f(i,j-1)-4f(i,j)]/4,	ans=[-6 -9 -4; -6 -9 -4; 2, -1 4]
% 对于左下角的点, I(i,j)=(u(i+2,j)+u(i,j+2)+2*u(i,j))/4-(u(i+1,j)+u(i,j+1))/2
% 对于左边界点, I(i,j)=(u(i+1,j)+u(i-1,j)+u(i,j+1)+u(i,j))/4-(u(i,j)+u(i,j+1))/2

对于左下角的点 $I(i,j)=\frac{u(i+2,j)+u(i,j+2)+2\ast u(i,j)}{4}-\frac{u(i+1,j)+u(i,j+1)}{2}$
对于左边界点 $I(i,j)=\frac{u(i+1,j)+u(i-1,j)+u(i,j+2)+u(i,j)}{4}-\frac{u(i,j)+u(i,j+1)}{2}$

积分运算

数值积分内容回顾

矩形公式：$L_n=h{\sum }_{k=0}^{n-1}{f}_k,R_n=h{\sum }_{k=1}^n{f}_k$；
梯形公式：$T_n=h{\sum }_{k=1}^{n-1}{f}_k+\frac{h}{2}\left(f_0+f_n\right)$；
中点法：$M_n=h{\sum }_{k=0}^{n-1}f(x_{k+\frac{1}{2}})$；
在a,b两点间，辛普森公式：$S=\frac{h}{6}(f(a)+4f(\frac{a+b}{2})+f(b))$；
在a,b区间内，复合辛普森公式：$S=\frac{h}{12}(f(a)+4f(\frac{3a+b}{4})+\frac{a+b}{2}+4f(\frac{a+3b}{4})+f(b))$。

梯形积分 trapz $T=h{\sum }_{k=1}^{n-1}{f}_k+\frac{h}{2}\left(f_0+f_n\right)$

%% 梯形积分 trapz
% 正如我们在数值积分篇讲过的梯形积分, 对于列表，我们同样可以将公式带入求其积分
a = [1 4 5 7 8 9];
trapz(a)	% ans = 29
x = [0.3: 0.01: 0.4];
y=x.^2;
trapz(y)	% ans = 1.2335

% 对于矩阵, trapz对列向量积分, trapz([],2)可对行向量积分
b = [1 3 4; 4 6 7; 2 1 7];
trapz(b)	% ans = [5.5000 8.0000 12.5000]

%% 累计梯形积分 cumtrapz
% 累计梯形积分的第n个元素是原矢量前n个元素的梯形积分
cumtrapz(b)	% ans = [0 0 0; 2.5000 4.5000 5.5000; 5.5000 8.0000 12.5000]

函数积分 quad, quadl

quad函数使用自适应辛普森算法，可以自动调整步长。

辛普森算法为 ${\int }_a^{b}f(x)\mathrm{d}x\approx \frac{b-a}{6}\left[f(a)+4f(\frac{a+b}{2})+f(b)\right]$，而我们可以知道积分区间越小，其值越准确，但相应的也会增加计算量，因此我们决定均衡二者，当在区间[a,b]内的积分近似等于区间[a,c]与区间[c,b]的积分和即$\mid {\int }_a^{b}f(x)\mathrm{d}x-[{\int }_a^{c}f(x)\mathrm{d}x+{\int }_c^{b}f(x)\mathrm{d}x]\mid <ϵ$时，该区间积分完成，否则对拆分后的小区间继续重复上述过程。这样的算法可自动适应被积函数，在被积函数变化剧烈处，将区间划分较密，在被积函数变化缓慢处，区间便比较稀疏了。

quadl函数则使用精度更高的自适应洛巴托(Lobatto)法，也称高斯积分法。

%% quad, quadl
clc;clear all;close all
% f=inline('exp(x.^(-3))','x');		% 建立积分函数
f=@(x)exp(x.^(-3));		% 使用@定义的匿名函数可以生成更高效的程序
format long
quadl(f,0.5,0.6)

%% 二重积分 dblquad (double->dbl)
ff=@(x,y)(y.*sin(x)+x.*cos(y));
dblquad(ff,pi,2*pi,0,pi)

%% 三重积分 triplequad
fff=@(x,y,z)(y*sin(x)+z*cos(y));
triplequad(fff,0,pi,0,1,-1,1)

符号工具箱

MATLAB也能使用符号运算工具箱实现求导函数和推导不定积分公式。

diff(differential) 符号变量微分，taylor 泰勒展开，int(integral) 符号变量积分，symsum 求级数和，limit 求极限，simple 将表达式化简。

符号工具箱内函数用法见：MATLAB解方程

总结

正确理解数值微分和数值积分的计算方法对数值计算极其重要，它们是数值计算的逻辑，如果对这部分概念不清楚则很可能在后续的编程中出现数值计算失控的情况。