贝塞尔曲线的python实现（简单易理解）

简介

贝塞尔曲线在计算机图形学中被大量使用，通常可以产生平滑的曲线。比如ps中的钢笔工具，就是利用的这种原理。由于用计算机画图大部分时间是操作鼠标来掌握线条的路径，与手绘的感觉和效果有很大的差别。即使是一位精明的画师能轻松绘出各种图形，拿到鼠标想随心所欲的画图也不是一件容易的事。这一点是计算机万万不能代替手工的工作，所以人们只能颇感无奈。使用贝塞尔工具画图很大程度上弥补了这一缺憾。贝塞尔曲线是计算机图形图像造型的基本工具，是图形造型运用得最多的基本线条之一。通过在二维平面上放置几个锚点，根据锚点的路径和描绘的先后顺序，产生直线或者是光滑曲线的效果。

一阶曲线

$$B_1(t)=P_0+(P_1-P_0)t$$$$B_1(t)=(1-t)P_0+t{P}_1,t\in [0,1]$$

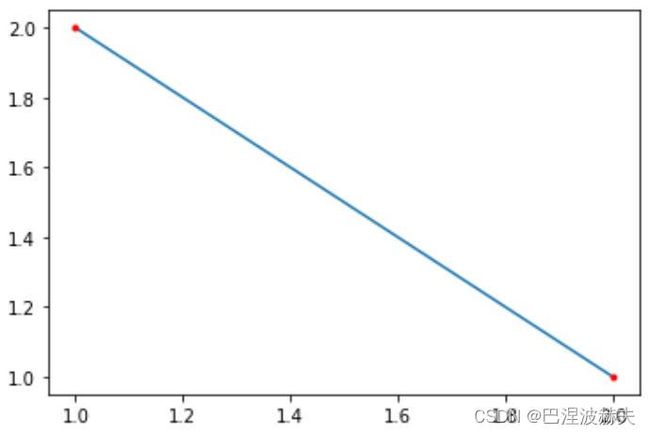
一阶曲线就是很好理解, 就是根据t来的线性插值. P0表示的是一个向量 [x ,y], 其中x和y是分别按照这个公式来计算的。

import matplotlib.pyplot as plt
import numpy as np

points = np.array([[1,2],[2,1]])# 在此处修改坐标
t = np.linspace(0,1,1000)
t = np.array([t,t]).T
B1 = (1-t)*points[0]+t*points[1]

plt.plot(B1[:,0],B1[:,1])
plt.plot(points[:,0],points[:,1],'r.')
plt.show()

n阶曲线

$$B_{i,n}(t)=C_n^i{t}^i(1-t{)}^{n-i}=\frac{n!}{i!(n-i)!}{t}^i(1-t{)}^{n-i},i=0,1,\cdots ,n$$$$P(t)=\sum _{i=0}^n{P}_i{B}_{i,n}(t,t\in [0,1])$$

实现方法1（numpy版本）

import matplotlib.pyplot as plt
import numpy as np

def getB(i):
    t = np.math.factorial(n)*init_t**i*(1-init_t)**(n-i)/(np.math.factorial(i)*np.math.factorial(n-i))
    return np.array([t,t]).T

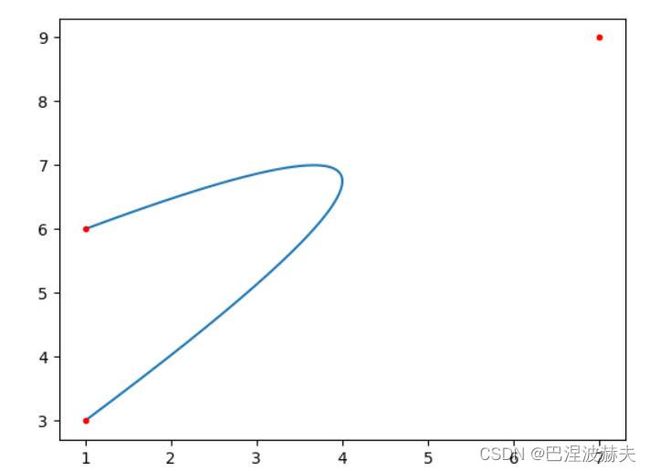
points = np.array([[1,3],[7,9],[1,6]])# 在此处修改坐标
n = points.shape[0]-1
init_t = np.linspace(0,1,1000)
P = np.zeros((1000,2))
for i in range(n+1):
    P += getB(i)*points[i]

plt.plot(P[:,0],P[:,1])
plt.plot(points[:,0],points[:,1],'r.')
plt.show()

实现方法2（易读版本）

from math import factorial
import matplotlib.pyplot as plt

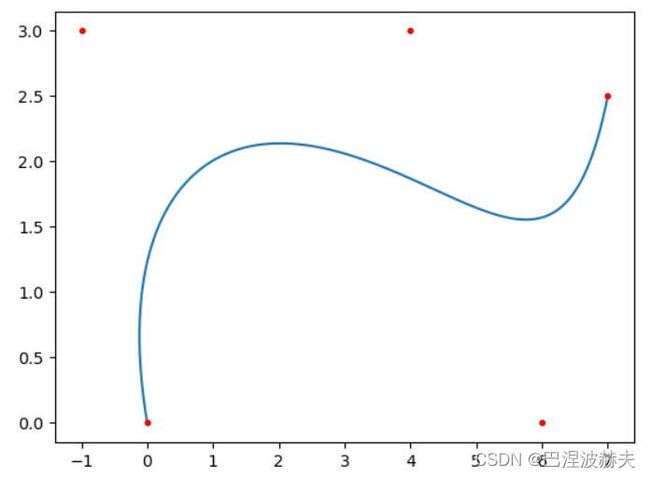
points = [[0,0],[-1,3],[4,3],[6,0],[7,2.5]]# 在此处修改坐标
N = len(points)
n = N - 1 
px = []
py = []
for T in range(1001):
    t = T*0.001
    x,y = 0,0
    for i in range(N):
        B = factorial(n)*t**i*(1-t)**(n-i)/(factorial(i)*factorial(n-i))
        x += points[i][0]*B
        y += points[i][1]*B
    px.append(x)
    py.append(y)

plt.plot(px,py)
plt.plot([i[0] for i in points],[i[1] for i in points],'r.')
plt.show()