青铜时代 —— 相机算法
文章目录
- `3A技术`
- 自动白平衡 AWB
-
-
- 定理
- 灰度世界算法
-
- 流程:
- 完美反射算法
-
- 流程
- 动态阈值算法
- 基于色温估计的AWB
-
- 原理
- 色温曲线
- 色温计算
-
- 流程
-
- 自动对焦 AF
-
- 重要性
- 流程
- 常用清晰度评价函数
- 状态机
- 自动曝光 AE
-
- 流程
- Denoise & Sharpness
-
- 双边滤波 Bilateral Filter
- 导向滤波 Guided Filter
-
- 原理
- 流程
- 暗通道去雾算法 + 导向滤波
-
- 暗通道先验
- 算法
- 导向滤波
- 图像融合 + 导向滤波
- 流程
- HDR
-
- 多曝光合成
- LTM
-
- 全局
- 局部
- 目前的色调映射算法
- SuperNight
- 双目相机定位
- 小波相关
- 基于特征的`配准标定`
- 由`运动`到结构 Structure From Motion SFM
- 稠密`运动`估计
-
- 平移配准的误差度量
- 光流
- 亮度恒常性
- 邻域光流相似假设
- 稠密光流 — Farneback
- 图像`拼接`
- 摄影学 (HDR等)
- `立体`视觉
- *3D重建
3A技术
- 自动对焦(AF)、自动曝光(AE)及自动白平衡(AWB)
自动白平衡 AWB
定理
- 在同一色温环境中如果对一幅自色图像进行白平衡校正后.那么对于其他非白色图像就都能真实的再现物体的颜色,并且其颜色的色差值是唯一的
- 利用色差值已知的非白色(R.B.G不为零)物体为参照物,同样可以实现白平衡处理
灰度世界算法
- 假设:对于一幅有着大量色彩变化的图像, R、 G、 B 三个分量的平均值趋于同一个灰度K。
流程:
- 确定
K- 固定值,取各通道最大值的一半,即127或128
- 取K为RGB三通道平均值的均值
- 计算各通道的增益
- K r = K / R a v e r K_r = K / R_{aver} Kr=K/Raver
- 校正各通道的值:
- Von Kries对角模型:两种不同的光照形成的图像可以通过对角矩阵转换
- R n e w = R × K r R_{new} = R × K_r Rnew=R×Kr
- 对于溢出的处理:
- 截断 255 整体偏白 建议使用√
- 线性变换,压缩到[0,255],整体偏暗,不建议
完美反射算法
- 完美全反射理论perfect Reflector假设图像上最亮点就是白点,并以此白点为参考对图像进行自动白平衡,最亮点定义为R+G+B的最大值
流程
- 计算每个像素的R\G\B之和,并保存到一临时内存块中
- 按R+G+B值的大小计算出其前
10%(或其他)的白色参考点的的阈值T - 遍历图像中的每个点,计算其中R+G+B值大于T的所有点的R\G\B分量的累积和的平均值
- 对每个点将像素量化到[0,255]之间(利用上述的通道均值,归一化到0!255)
动态阈值算法
- A Novel Automatic White Balance Method For Digital Still Cameras
- 流程和经典算法相同:白点检测 + 白点调整 参考
- 主要就是白点检测部分的算法,在YCbCr中进行!

基于色温估计的AWB
原理
- 色温是光线在不同的能量下,人们眼睛所感受到的颜色变化,以开尔文(K)为色温计算单位,简单说就是光线的颜色

- 人类的眼睛有很好的适应性,能统一不同光照下的物体颜色!
- 相同的物体在不同的色温光源下呈现出相同的颜色,这就称为色彩恒常性
- 白平衡的调整过程其实就是通过调色温来实现的,所以色温对于数码相机而言就是白平衡的问题,AWB算法的核心就是判断图像的色温
色温曲线
- 流程
- 在各个色温下(2500~7500)拍几张
白纸照片,假设拍6张(2500,3500…7500),可以称作色温照 - 把色温照进行矫正,具体是对R/G/B通道进行轿正,让偏色的白纸照变成白色,并记录各个通道的矫正参数. 实际上只矫正R和B通道就可以,这样就得到了6组矫正参数(R-gain,B-gain).
- 上面是做前期工作,爱思考的小明发现,只要知道当前场景是什么色温,再轿正一下就可以了.事实上也就是如此.
- (进一步插值得到色温曲线): 色温 - RG-gain - BG-gain


色温计算
流程
- 图像分块MxN,统计每块的基本信息(白色像素数量+RGB通道分量均值)
- 设定白色的颜色范围,1,如果块中的白色像素太少,可以抛弃掉. 2,如果白色像素太多,多到每一个像素点都是,那也要抛弃掉,因为很可能在该区域过曝了
- 找出所有白块,根据色温曲线判断色温(找到所有白色块到曲线的距离进行加权,为防止误判对不同块根据统计信息进行权重设置,如根据统计信息中白点数)
- 取色温众数当作当前色温,根据色温曲线得到R-gain和B-gain
自动对焦 AF
重要性
- 采集到的图像是否清晰,直接决定了成像系统的成像质量。
- 调焦就是通过调节成像系统中的参数(像距、物距、焦距),使镜头与成像面的距离发生改变,使成像过程满足物像关系,获得最清晰的准焦图像。
- 自动对焦:只需要根据图像清晰度判断镜头当前的状态,再控制调焦镜头移动,完成自动对焦
- 传统对角是基于测距进行
- 本文关注于基于数字图像的AF
流程
- 对离焦信号进行特征提取,采用调制梯度作为自动对焦评价函数。
- 空间域卷积/反卷积变换的离焦深度法,解决了频域计算运算量大的问题
- 准焦图像包含清晰的边缘和纹理信息,自相关峰值曲线是高且窄的
- 采用平方梯度函数测量离焦模糊图像的高频成分再利用尺子搜索法来寻找准焦位置
常用清晰度评价函数
- 常用的清晰度评价算法有:
- 频域函数 :对焦越好、高频部分越多,细节越多,图像越清晰。
- 灰度函数 :对焦越好,和周围相邻灰度点差值越大,边缘越清晰,图像越清晰。对比度
- 信息熵函数:对焦越好,图像包含的信息熵越大,包含信息量更大,图像越清晰。
- 统计学函数:对焦越好,直方图多样性越好,图像越清晰
状态机
- 对焦算法中,基本都是在不停的做状态机查询,常用的状态有:
1、等待对焦触发
2、对焦参数更新(如图像分辨率变化或者对焦ROI坐标变化)
3、对焦工作中
4、对焦状态返回(对焦成功或者失败)
参考
自动曝光 AE
- 自动曝光就是相机代替人的操作,自动调节曝光时间、光圈、ISO进行曝光,使得所摄物体亮度正常。这句话解释起来很简单,但是存在两个难点问题:第一,相机不如人眼这样可以直观的分辨图像明暗,如何判断这幅图像是否亮度合适;第二,如何调整曝光时间、光圈、ISO,这三者调节的比例
流程
- 对当前图像进行亮度统计;
- 根据当前图像亮度确定曝光值
- 计算新的曝光参数,曝光时间、光圈、增益
- 将新的曝光参数应用到相机
- 重复步骤一到四,直到亮度满足要求
Denoise & Sharpness
- 保边滤波
双边滤波 Bilateral Filter
- 双边滤波与高斯滤波器相比,对于图像的边缘信息能过更好的保存。其原理为一个与空间距离相关的高斯函数与一个灰度距离相关的高斯函数相乘。
- 空间距离:指的是当前点与中心点的欧式距离
- 灰度距离:指的是当前点灰度与中心点灰度的差的绝对值
e − ( x i − x c ) 2 + ( y i − y c ) 2 2 σ 2 e − ( g r a y ( x i , y i ) − g r a y ( x c , y c ) ) 2 2 σ 2 \mathrm{e}^{-\frac{\left(x_{i}-x_{c}\right)^{2}+\left(y_{i}-y_{c}\right)^{2}}{2 \sigma^{2}}} \\ \mathrm{e}^{-\frac{\left(g r a y\left(x_{i}, y_{i}\right)-g r a y\left(x_{c}, y_{c}\right)\right)^{2}}{2 \sigma^{2}}} e−2σ2(xi−xc)2+(yi−yc)2e−2σ2(gray(xi,yi)−gray(xc,yc))2 - 双边滤波中加入了对灰度信息的权重,即在邻域内,灰度值越接近中心点灰度值的点的权重更大,灰度值相差大的点权重越小。此权重大小,则由值域高斯函数确定。
- 两者权重系数相乘,得到最终的卷积模板。由于双边滤波需要每个中心点邻域的灰度信息来确定其系数,所以其速度与比一般的滤波慢很多,而且计算量增长速度为核大小的平方。
- 双边 保边不保梯度 因为边缘梯度变化急剧的情况下 会出现像素值差距过大导致最后算出权值的不稳定!
导向滤波 Guided Filter
参考
- 导向滤波(Guided Fliter)显式地利用 guidance image 计算输出图像,其中 guidance image 可以是输入图像本身或者其他图像。导向滤波比起双边滤波来说在边界附近效果较好;另外,它还具有 O(N) 的线性时间的速度优势
- 保梯度
原理
- p为输入图像,I 为导向图,q 为输出图像,n噪声
- 重要假设是输出图像 q q q 和引导图像 I I I 在滤波窗口 w k w_{k} wk 上存在局部线性关系:
q i = a k I i + b k , ∀ i ∈ ω k q i = p i − n i \begin{array}{c} q_{i}=a_{k} I_{i}+b_{k}, \forall i \in \omega_{k} \\ q_{i}=p_{i}-n_{i} \end{array} qi=akIi+bk,∀i∈ωkqi=pi−ni - 最小化噪声。对于每一个滤波窗口,该算法在最小二乘意义上的最优化可表示为(岭回归):
E ( a k , b k ) = ∑ i ∈ ω k ( ( a k I i + b k − p i ) 2 + ϵ a k 2 ) E\left(a_{k}, b_{k}\right)=\sum_{i \in \omega_{k}}\left(\left(a_{k} I_{i}+b_{k}-p_{i}\right)^{2}+\epsilon a_{k}^{2}\right) E(ak,bk)=i∈ωk∑((akIi+bk−pi)2+ϵak2) - 求导得到闭合解求解:
a k = 1 ∣ ω ∣ ∑ i ∈ ω k I i p i − μ k p ˉ k σ k 2 + ϵ b k = p ˉ k − a k μ k a_{k}=\frac{\frac{1}{|\omega|} \sum_{i \in \omega_{k}} I_{i} p_{i}-\mu_{k} \bar{p}_{k}}{\sigma_{k}^{2}+\epsilon} \\ b_{k}=\bar{p}_{k}-a_{k} \mu_{k} ak=σk2+ϵ∣ω∣1∑i∈ωkIipi−μkpˉkbk=pˉk−akμk - 其中: μ k \mu_{k} μk 和 σ k 2 \sigma_{k}^{2} σk2 分别表示引导图像 I I I 在窗口 w k w_{k} wk 中的平均值和方差, ∣ w ∣ |w| ∣w∣ 是窗口 w k w_{k} wk 中像素点的个数, p ˉ k = \bar{p}_{k}= pˉk= 1 ∣ w ∣ ∑ i ∈ w k p i \frac{1}{|w|} \sum_{i \in w_{k}} p_{i} ∣w∣1∑i∈wkpi 是输入图像在窗口 w k w_{k} wk 中的平均值。
- 窗口里。比如,如果用3*3的窗口滤波, 那么除了边易区域的每个点都会被包含在9个窗口里。因此,对于不 的窗口,我们将会得到 ∣ w ∣ |w| ∣w∣个 q i q_{i} qi 值, 就对所有的 q i q_{i} qi 值取平均,得到最终结果:
q i = 1 ∣ ω ∣ ∑ k ∣ i ∈ ω k ( a k I i + b k ) q_{i}=\frac{1}{|\omega|} \sum_{k | i \in \omega_{k}}\left(a_{k} I_{i}+b_{k}\right) qi=∣ω∣1k∣i∈ωk∑(akIi+bk) - 边缘保持能力:对于该算法,当 I = p I=p I=p时,即输入图像和引导图像是同一副图像时,该算法即成为一个边缘保持滤波器。
a k = σ k 2 σ k 2 + ϵ b k = ( 1 − a k ) p ˉ k a_{k}=\frac{\sigma_{k}^{2}}{\sigma_{k}^{2}+\epsilon} \\ b_{k}=\left(1-a_{k}\right) \bar{p}_{k} ak=σk2+ϵσk2bk=(1−ak)pˉk - ϵ \epsilon ϵ在这里相当于界定平滑区域和边缘区域的阈值
- Case 1:平坦区域,如果在某个滤波賓口内,该区域是相对平滑的,方差 σ k 2 \sigma_{k}^{2} σk2 将远远小于 ϵ ∘ \epsilon_{\circ} ϵ∘ 从而 a k ≈ a_{k} \approx ak≈ 0 , b k ≈ p ˉ k 0, b_{k} \approx \bar{p}_{k} 0,bk≈pˉk 。相当于对该区域作均值滤波。
- Case 2:高方差区域,相反,如果该区域是边易区域,方差很大, σ k 2 \sigma_{k}^{2} σk2 将远远大于 ϵ \epsilon ϵ 从而 a k ≈ 1 , b k ≈ a_{k} \approx 1, b_{k} \approx ak≈1,bk≈ 0,相当于在区域保持原有梯度!
流程
暗通道去雾算法 + 导向滤波
暗通道先验
- 暗通道先验是基于如下观察,在户外的无雾图像中,在大部分非天空区域,至少有一个通道值是很小一个数或趋近于零。

- 首先对图像每个像素取三通道中最小值,得到一个单通道图,然后对这个单通道图作最小值滤波就可以得到暗通道图 J d a r k J^{dark} Jdark
- 正因为自然界总是充满了彩色和阴影,就导致了图像暗通道总是很暗
算法
I ( x ) = J ( x ) t ( x ) + A ( 1 − t ( x ) ) I(x)=J(x) t(x)+A(1-t(x)) I(x)=J(x)t(x)+A(1−t(x))
- 表示有雾图像,J是要恢复的无雾的图像,A是全球大气光成分, t(x)为透射率
- 晴天和雾天的区别只是大气光成分的多少,表达在这个式子里就是透射率。晴天的时候大气光成分少,物体反射光的透射率很高,几乎让人感受不到大气光成分的存在。雾天则相反
- 该模型几乎就是两个图层在不同透明度下的叠加。可以设透明度为 α \alpha α

导向滤波
- 以原图灰度图作为导向图,对透射率图进行导向滤波,可以得到非常精细的透射率图,从而得到高质量的去雾图。这里再以之前人为生成的“雾图”说明导向滤波的效果!
图像融合 + 导向滤波
参考
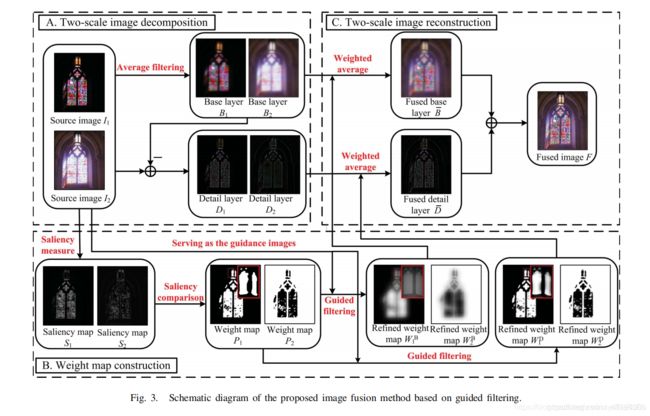
- Image Fusion with Guided Filtering - 2013
- 融合的对象可以是多光谱图像,不同焦点的图像,不同曝光的图像等。
- 论文比较创新点就是提出了一种不同幅图像的权重计算方法,引入了像素显著性和图像空间连续性的概念。
- 并且使用了引导滤波来重建权重,最终得到了高效和不错的融合效果。
流程
- 1 Two-Scale Image Decomposition(双尺度分解):一个简单的均值滤波来获取图像的基层和细节层,滤波器越大,得到的基层模糊程度越高。而细节层是原图减去基层图,随着滤波半径的增大,细节层的信息也会相应增加。论文中给出的建议滤波器大小为31×31
- 2 Weight Map Construction With Guided Filtering(构建权重图):利用导向滤波进行权重重建,上述流程图中应该是各个通道单独处理的,这里直接放一起处理了。
- 对原图进行拉普拉斯滤波(3×3)得到高频细节,然后再对得到的高频细节进行一次高斯滤波(11×11,sigma=5)
- 像素显著性和空间连续性:

P n k = { 1 if S n k = max ( S 1 k , S 2 k , … , S N k ) 0 otherwise P_{n}^{k}=\left\{\begin{array}{ll} 1 & \text { if } S_{n}^{k}=\max \left(S_{1}^{k}, S_{2}^{k}, \ldots, S_{N}^{k}\right) \\ 0 & \text { otherwise } \end{array}\right. Pnk={10 if Snk=max(S1k,S2k,…,SNk) otherwise - 对权重值进行导向滤波:由于多个图像间容易产生噪声,并可能存在不完全对齐等问题,很容易造成融合后的图像有伪影等,因此在基于空间连续性的思想下,需要对得到的权重图进行导向滤波。关于导向滤波的最优参数,作者并没有给出,但是不同层的权重图将用不同参数进行滤波
- 3 Two-Scale Image Reconstruction(融合重建)
- 对两个尺度层分别加权,然后相加就得到了最后的输入。在相加前,将每个像素点的权重之和,归化到1
HDR
- 现实真正存在的亮度差,即最亮的物体亮度,和最小的物体亮度之比为108, 而人类的眼睛所能看到的范围是105左右,但是一般的显示器,照相机能表示的只有256种不同的亮度,计算一般的显示器,照相机能表示的只有256种不同的亮度机在表示图象的时候是用8bit(256)级或16bit(65536)级来区分图象的亮度的,但这区区几百或几万无法再现真实自然的光照情况。
- HDR文件是一种特殊图形文件格式,它的每一个像素除了普通的RGB信息,还有该点的实际亮度信息。
- 线性映射导致细节丢失
- Fast Bilateral Filtering for the Display of High-Dynamic-Range Images
多曝光合成
- 参考
- 流程
- 捕获不同曝光度的多张图像:1 曝光不足的图像:该图像比正确曝光的图像更暗。 目标是捕捉非常明亮的图像部分。2 正确曝光的图像:这是相机将根据其估计的照明拍摄的常规图像。3 曝光过度的图像:该图像比正确曝光的图像更亮。 目标是拍摄非常黑暗的图像部分。
- 对齐图像:合成 HDR 图像时使用的图像如果未对齐可能会导致严重的伪影(Ghost)。由于亮度不同,所以先要转化到一个亮度无关的空间上去进行对齐;Opencv中提供AlignMTB算法:将所有图像转换为中值阈值位图median threshold bitmaps(MTB)。 图像的 MTB 生成方式为将比中值亮度的更亮的分配为 1,其余为 0。 MTB 不随曝光时间的改变而改变。 因此不需要我们指定曝光时间就可以对齐 MTB
- 提取相机响应函数Camera Response Function(CRF):相机响应不是线性的(灰度值和亮度不是线性关系)。如果我们知道每个图像的曝光时间,则可以从图像估计 CRF(最优化问题!),Opencv中采用CalibrateDebevec

- 合并图像,Opencv中MergeDebevec ,合成的规则:比如根据亮度来选择不同图中的区域;为了无缝的进行融合,可以采用金字塔分解合成的方式;
- 色调映射:将高动态范围(HDR)图像转换为 8 位单通道图像的过程称为
色调映射。将 [ 0 , i n f ) [0, inf) [0,inf) > [ 0 , 255 ] [0,255] [0,255],Opencv中实现了四个:Drago色调映射 + Durand色调映射(基础层和细节层。 使用称为双边滤波器的边缘保留滤波器来获得基本层) + Reinhard色调映射 + Mantiuk色调映射- 最简单的就是gamma变换,但是容易导致色彩的欠饱和,所以先将图像分成亮度图和色度图,全局映射亮度图,在恢复会好点!
- 亮度图的全局映射:亮度图取对数 + 低通滤波获得基底层 + 高通滤波得到细节层 + 基地层进行放缩 + 加上细节层得到亮度对数图!
- 还可以采用边界保持的滤波器来产生基底层,如双边滤波,替代亮度层的低通滤波器!
- 还可以压缩梯度方法获取基底层(Fattal 2002)!对亮度对数图求差分得到梯度场,乘上一个空间衰减函数(减弱大范围的亮度变化),再结合原图的梯度场得到最终的梯度场!…
- 最简单的就是gamma变换,但是容易导致色彩的欠饱和,所以先将图像分成亮度图和色度图,全局映射亮度图,在恢复会好点!
LTM
- 局部色调映射(Local Tone Mapping)
- 重建视觉外观是色调映射的终极目标。色调映射算法在降低高动态图像(HDR)范围的同时着力保护捕捉到的原始图像的外观。色调映射算子分两种策略,一种是全局的,另一种是局部的。
全局
- 每一个像素点将会根据它的全图特征和亮度信息进行映射,不管其空间位置几何。全局算子一个比较典型的例子就是
色调曲线。 - 全局色调映射在处理12位(12-bit)深度的图像的时候是完全OK的,当图像的动态范围特别高的时候,那就不行了。这是因为所有的像素点都采取同一种方式进行处理,根本就没有管它是在较亮区域还是较暗区域。这样的话,就是导致图像色调映射过后看起来很平坦,失去了其局部的细节信息。
局部
- 像素点所在的空间位置会被考虑,在进行尺度变换的时候
- 局部色调映射需要考虑到每个像素点周围的亮度信息,这样这会使得计算量和内存的使用会更大,但是会有更好的结果。如果处理得当,局部色调映射会很好的保护高亮和阴影部分的局部对比度和细节信息。
目前的色调映射算法
- 伽马压缩算法 (全局)
- 基于直方图均衡的压缩算法 (全局)
- 基于Retinex的算法:参考 retinex是以色感一致性(颜色恒常性)为基础的。不同于传统的线性、非线性的只能增强图像某一类特征的方法,Retinex可以在动态范围压缩、边缘增强和颜色恒常三个方面打到平衡,因此可以对各种不同类型的图像进行自适应的增强



- 基于梯度高动态压缩算法,这些算法的侧重点在于对比度的保持而不是亮度的映射,这种方法的思路起源于人眼对于对比度或者不同亮度区域的亮度比例最为敏感。这种色调映射由于较好地保存了对比度细节,所以通常会产生非常锐利的图像,但是这样做的代价是使得整体的图像对比度变得平缓。Gradient Domain High Dynamic Range Compression
- 翻译
- 我们的算法是基于一个相当简单的观察,即在一个高动态范围内亮度的任何剧烈变化都必须在某个尺度上产生较大的亮度梯度。另一方面,精细的细节,如纹理,对应的梯度要小得多(图像金字塔)
- 求解图片梯度场
- 对修改梯度场数值对比度(不修改方向) 梯度衰减函数,我们希望衰减是渐进的,大幅度的衰减比小的衰减更大。
- 泊松方程第二类边界条件,根据散度值重建
- 等
SuperNight
- “超级夜模式”通过突出较暗区域的细节,生成更明亮、更丰富多彩的图像,提高了夜间和低光条件下拍摄的图像质量。
- IPhone XS 拍摄图

- 这些技术大都基于造就 “夜视” 功能的 HDR+ 进行构建
- 昏暗场景下摄影经历的人对图像噪声定然不陌生,这种噪声看上去就像是像素间亮度的随机变化 >
散粒噪声 - 将击中每个像素的光线所产生的电子电荷转换为数字时引入的随机错误 >
读出噪声 - 信噪比 (SNR),衡量图像从这些亮度变化中的突显程度
S N R = ∑ x = 0 M − 1 ∑ y = 0 N − 1 f ( x , y ) 2 / ∑ x = 0 M − 1 ∑ y = 0 N − 1 ( f ( x , y ) − g ( x , y ) ) 2 R M S E = 1 m × n ∑ i m ∗ n ( f i − g i ) 2 P S N R = 10 log 10 M N ∥ f − f ^ ∥ 2 S S I M = SNR = \sum_{x=0}^{M-1} \sum_{y=0}^{N-1} f(x, y)^{2} / \sum_{x=0}^{M-1} \sum_{y=0}^{N-1}(f(x, y)-g(x, y))^{2} \\ RMSE=\sqrt{\frac{1}{m×n} \sum_{i}^{m * n}\left(f_i - g_i\right)^{2}} \\ PSNR=10 \log _{10} \frac{M N}{\|f-\hat{f}\|^{2}} \\ SSIM = SNR=x=0∑M−1y=0∑N−1f(x,y)2/x=0∑M−1y=0∑N−1(f(x,y)−g(x,y))2RMSE=m×n1i∑m∗n(fi−gi)2PSNR=10log10∥f−f^∥2MNSSIM= - 2014 HDR+,可通过捕捉连拍帧、在软件中进行校准并将之合并,进而改善此种情况。HDR+ 的主要目的是改进动态范围,这意味着我们将能拍摄呈现各类亮度的场景(如日落或逆光人像)
双目相机定位
- 测距原理图:

T x Z = T x − [ ( u l − u 0 ) d x + ( u 0 − u r ) d x ] Z − f Z = T x u l − u r ⋅ f d x \begin{array}{l} \frac{T_{x}}{Z}=\frac{T_{x}-\left[\left(u_{l}-u_{0}\right) d x+\left(u_{0}-u_{r}\right) d x\right]}{Z-f} \\ Z=\frac{T_{x}}{u_{l}-u_{r}} \cdot \frac{f}{d x} \end{array} ZTx=Z−fTx−[(ul−u0)dx+(u0−ur)dx]Z=ul−urTx⋅dxf
d x dx dx 为像素的物理尺寸 , f , f ,f 为焦距, T x T_{x} Tx 为左右相机的基线长度
经过之前的标定工作, 我们已经得到了 f d x \frac{f}{d x} dxf 和 T x , T_{x}, Tx, 要计算一个物体上某一点的深度Z, 只需要知道其在左右相片 上的像素坐标就可以了 - 摄像机标定:
- 内参标定:摄像机内参反映的是摄像机坐标系到图像坐标系之间的投影关系(张正友标定法:A Flexible New Technique for Camera Calibration)
- 外参标定:摄像机外参反映的是摄像机坐标系和世界坐标系之间的旋转R和平移T关系。
- 利用特征点检测和匹配方法,解出内参矩阵和本质矩阵,用本质矩阵E解算出两个摄像机之间的Rotation和Translation,也就是两个摄像机之间的外参。
- 双目图像校正
- 畸变校正
- 立体校正:① 得到两个摄像机之间的 Rotation和Translation之后,要用下面的API(stereoRectify)对两幅图像进行立体对极线校正,这就需要算出两个相机做对极线校正需要的R和T,用R1,T1, R2, T2表示,以及透视投影矩阵P1,P2:② 得到上述参数后,就可以使用下面的API进行对极线校正操作了,并将校正结果保存到本地:
- 立体匹配获得视差图:可以使用OpenCV中的BM算法或者SGBM算法计算视差图。由于SGBM(Semi-Global Block Matching)算法的表现要远远优于BM算法,因此采用SGBM算法获取视差图。
- 视差图进行空洞填充:视差值不可靠的视差大多数是由于遮挡引起,或者光照不均匀引起。空洞填充也有很多方法,可用附近可靠视差值的均值进行填充。先用大窗口再与小窗口填充!
- 视差图转换为深度图:视差的单位是像素(pixel),深度的单位往往是毫米(mm)表示; depth = ( f * baseline) / disp ,depth表示深度图;f表示归一化的焦距,也就是内参中的fx; baseline是两个相机光心之间的距离,称作基线距离;disp是视差值
小波相关
- 与常规的带通金字塔相比,小波的方向选择性更佳
- 传统金字塔过于完备,即使用比原始图像多得多的像素描述空间和频域的多分辨率,而小波更加紧致,能保持分解的图像和原图像大小相同,有一写小波族也是过于完备的!以提供更好的移位能力和方向导向!
- 所谓的小波的小是针对傅里叶波而言,傅里叶波指的是在时域空间无穷震荡的正弦(或余弦波)
- 相对而言,小波指的是一种能量在时域非常集中的波,它的能量有限,都集中在某一点附近,而且积分的值为零,这说明它与傅里叶波一样是正交波。
- 小波:小区域、长度有限、均值为0的波形
- 小—是指它具有衰减性,波—指它的波动性,其振幅正负之间的震荡形式。正弦信号在傅立叶变换时没有衰减性。
- 傅立叶相比:小波变换是时间(空间)频率的局部化分析,它通过伸缩平移运算对信号(函数)逐步多尺度细化最终达到高频和低频的时间细分,能自动适应时频信号分析的要求,从而可聚焦信号的任意细节,解决了傅立叶变换的难题,称为“数学显微镜”。尺度越大,越窄;傅立叶变换:在频率域和时间域全部的集合上算的。
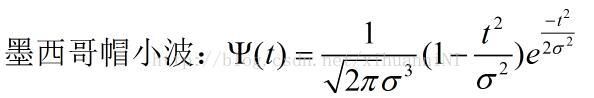
- 小波的尺度问题:低通滤波器:小波相当于伸展了,获得低频信号的特征,大致的轮廓特征;高通滤波器:小波相当于压缩了,获得高频信号的特征!

- Haar特征因为类似于Haar小波而得名,Haar-like features提取过程可看作对图像局部进行Haar小波变换,它反映了图像局部的灰度变化,当然不是直接进行变换,而通常是以一种简便的方式如积分图像。通常作目标检测/识别也不会是对图像整体进行Haar小波变换,而是将图像密集化为一些小块,在每个小块上做变换。对图像整体进行Haar小波变换分析系数当然也可做些边缘检测等工作。Haar型特征的计算是通过积分图像实现的!
基于特征的配准标定
- 给定两个已经配准的特征点集合,最简单的方法就是最小二乘!估计出运动参数!刚性和非刚性!
- 2D配准:最小二乘
- 给出几张图经过配准的特征点集合,估计2d和3d的变换
- 摄像头的姿态估计
- 摄像头的内标定
由运动到结构 Structure From Motion SFM
- 给出几幅图像及其特征点的稀疏对应,如何估计3d点的位置!
- 设计3d几何结构和摄像头姿态的同时估计
- 三角测量 + 二视图之间的关系(两个摄像头的极线几何)
- 因子分解法:特征轨迹恢复结构和运动
- 光束平差法:非线性最小化测量(重投影)
- 全局sfm主要包括以下步骤:
1.提取各张照片上的特征点及其描述;
2.对所有照片相互进行特征点匹配;
3.根据匹配的特征点计算照片i到照片j的相互位置关系(本质矩阵5点算法,或其它算法),得到view graph;
4.对相互位置关系进行准确性验证(validation check);
5.根据照片两两之间的匹配点数或者匹配误差,从view graph 中提取maximum spanning tree 用于计算各个照片在全局坐标系下的旋转初值;
6.通过view graph 进行rotation averaging获取各照片在全局坐标系下的旋转值;
7.使用全局旋转进行translation averaging获取各照片在全局坐标系下的平移量(或者同时获取了匹配点三维坐标值);
8.进行最终的光束平差优化。
稠密运动估计
- 早期使用基于块的平移配准方法(光流)
- 误差度量 + 搜索方法
平移配准的误差度量
- 最简单的是误差平移度量 SSD
- 这个误差度量就是模板匹配的度量准则,最常用的就是NCC归一化互相关们可以在傅里叶域加速运算

- 分层运动估计 —— 图像金字塔
- 傅里叶加速:相关操作可以用傅里叶加速,相位相关十分方便平移的检测!
- 对于图像的旋转和尺度变化,可以将图像转换为极坐标,在用傅里叶加速计算平移!
光流
- 每个像素的运动估计!
亮度恒常性
邻域光流相似假设
- 假设该邻域内的所有像素点光流值一致,通常,一个小的图像区域里像素移动方向和大小是基本一致的,因此,这个假设也是合理的。借助该假设,领域内的所有像素都有式(3-1-5)

- 基于亮度不变假设和邻域光流相似假设,为了解决图像偏移较大的情况,Lucas-Kanade算法还借助了图像金字塔(Pyramid)的方式,在高层低分辨率图像上,大的偏移将变为小的偏移。最终,Lucas-Kanade方法给出了一种求解稀疏(明显特征的角点)光流的方法。
稠密光流 — Farneback
- LK稀疏算法只需要每个感兴趣点周围小窗口的局部信息,这样就有一个问题,较大的运动会将点移除这个小窗口,从而造成算法无法再找到这些点。(所以才有了KLT的三个前提假设)
- 相邻帧之间的亮度恒定;
- 相邻帧之间物体的运动比较“微小”;
- 保持空间一致性;即,相邻像素点具有相同的运动
- 稀疏的关键点是计算角点,稠密的关键点是找图像上所有移动的点
- Farneback稠密光流的主要思想是利用多项式对每个像素的邻域信息进行近似表示

- Farneback 算法对于每帧图像中的每个像素点周围设定一个邻域(2n+1)×(2n+1),利用邻域内的共(2n+1)^2个像素点作为最小二乘法的样本点,拟合得到中心像素点的六维系数
参考
图像拼接
- 使用运动模型对图像进行配准
- 在摄影测绘中,同时调整有重叠的大量图像的姿态参数的过程叫做光束平差法,
全局配准 - 这个是同样方法
- 虽然匹配上了,但是仍然还会存在因视差导致的畸变重影模糊
摄影学 (HDR等)
- HDR
- 超分辨 + 去模糊
- 去马赛克
- 纹理分析与合成
立体视觉
- 历史:视觉感知 - 视差感知深度 - 视差和距离(深度)成反比
- 学习流程:
- 找到像素点的极线(计算这个像素在另一幅图像中的位置范围)
- 基于兴趣点和边缘类特征的稀疏立体视觉匹配方法,得到深度图
- 在视差图形式下估计出像素间稠密集合
- 选择一个像素的匹配准则
- 使用局部的基于区域的聚集或者全局的优化消除潜在匹配中的歧义
- 多视图立体视觉方法,建立一个完整的3D模型
*3D重建
- 多个深度图进行融合成3D模型
- 形状和表观模型