TensorFlow 2 线性回归

低阶API

TensorFlow 的低阶 API 实现，实际上就是利用最基本的函数和组件，结合 Eager Execution 机制来完成。实验首先初始化一组随机数据样本，并添加噪声，然后将其可视化出来。

import matplotlib.pyplot as plt
import tensorflow as tf
%matplotlib inline

TRUE_W = 3.0
TRUE_b = 2.0
NUM_SAMPLES = 100

# 初始化随机数据
X = tf.random.normal(shape=[NUM_SAMPLES, 1]).numpy()
noise = tf.random.normal(shape=[NUM_SAMPLES, 1]).numpy()
y = X * TRUE_W + TRUE_b + noise  # 添加噪声

plt.scatter(X, y)

输出的散点图如下：

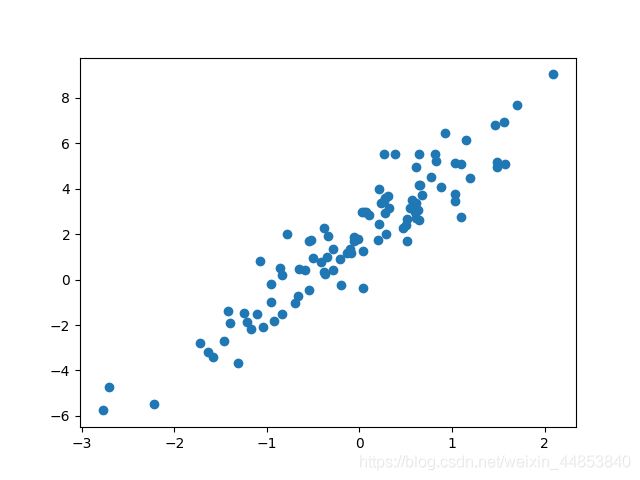
接下来定义一元线性回归模型：
$$f(w,b,x)=w\ast x+b$$

class Model(object):
    def __init__(self):
        self.W = tf.Variable(tf.random.uniform([1]))  # 随机初始化参数
        self.b = tf.Variable(tf.random.uniform([1]))
# self.valueName
# valueName：表示self对象，即实例的变量。与其他的，Class的变量，全局的变量，局部的变量，是相对应的。

# self.function()
# function：表示是调用的是self对象，即实例的函数。与其他的全局的函数，是相对应的。
    def __call__(self, x):
        return self.W * x + self.b  # w*x + b

此为标准的 TensorFlow 模型类的构建方法，后续的复杂神经网络构建过程还会不断地使用这一结构。

对于随机初始化的 $w$ 和 $b$，我们可以将其拟合直线绘制到样本散点图中：

model = Model()  # 实例化模型

plt.scatter(X, y)
plt.plot(X, model(X), c='r')

效果图如下：

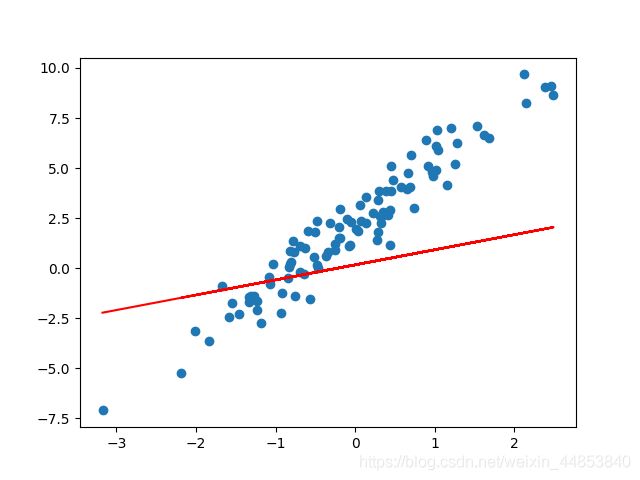
由于是随机初始化，极大概率直线无法准确拟合数据。然后，我们定义线性回归使用到的损失函数：
$$\mathrm{L}\mathrm{o}\mathrm{s}\mathrm{s}(w,b,x,y)=\sum _{i=1}^N(f(w,b,x_i)-y_i{)}^2$$
公式中，$f(w,b,x_i)$ 是模型根据 $x_i$ 计算的预测值，$y_i$ 则表示真实值。

def loss_fn(model, x, y):
    y_ = model(x)
    return tf.reduce_mean(tf.square(y_ - y))

接下来需要计算参数的梯度，然后使用梯度下降法来更新参数：

EPOCHS = 10  # 全部数据迭代 10 次
LEARNING_RATE = 0.1  # 学习率

for epoch in range(EPOCHS):  # 迭代次数
    with tf.GradientTape() as tape:  # 追踪梯度
        loss = loss_fn(model, X, y)  # 计算损失
    dW, db = tape.gradient(loss, [model.W, model.b])  # 计算梯度
    model.W.assign_sub(LEARNING_RATE * dW)  # 更新梯度
    model.b.assign_sub(LEARNING_RATE * db)

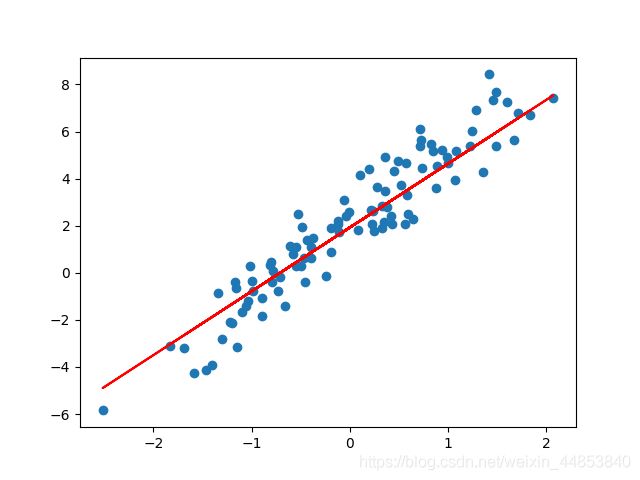
plt.scatter(X, y)
plt.plot(X, model(X), c='r')

效果图如下：

低阶 API 实现多项式回归：

from matplotlib import pyplot as plt
import numpy as np
import tensorflow as tf

# 给定散点样本
x = np.array([0.12, 0.21, 0.32, 0.41, 0.51, 0.62, 0.73, 0.86, 0.97, 0.99])
y = np.array([0.53, 0.57, 0.63, 0.70, 0.79, 0.91, 1.05, 1.246, 1.42, 1.51])


class Model(object): # 定义模型类
    def __init__(self):
        self.a = tf.Variable(tf.random.uniform([1]))  # 随机初始化参数
        self.b = tf.Variable(tf.random.uniform([1]))
        self.c = tf.Variable(tf.random.uniform([1]))

    def __call__(self, x):
        return self.a * x * x + self.b * x + self.c  
        # a*x^2 + b*x + c

def loss_fn(model, x, y): # 定义损失函数
    y_ = model(x)
    return tf.reduce_mean(tf.square(y_ - y))

EPOCHS = 20  # 全部数据迭代 20 次
LEARNING_RATE = 0.1  # 学习率

model = Model()  # 实例化模型

x = tf.constant(x, dtype=tf.float32) # 转换为张量
y = tf.constant(y, dtype=tf.float32) # 转换为张量

for epoch in range(EPOCHS):  # 迭代次数
    with tf.GradientTape() as tape:  # 追踪梯度
        loss = loss_fn(model, x, y)  # 计算损失
    da, db, dc = tape.gradient(loss, [model.a, model.b, model.c])  # 计算梯度
    model.a.assign_sub(LEARNING_RATE * da)  # 更新梯度
    model.b.assign_sub(LEARNING_RATE * db)
    model.c.assign_sub(LEARNING_RATE * dc)

X = tf.linspace(0.0, 1.0, 50)

plt.scatter(x, y)
plt.plot(X, model(X), c='r')

效果图如下：

高阶API

TensorFlow 2 中提供了大量的高阶 API 帮助我们快速构建所需模型，接下来使用一些新的 API 来完成线性回归模型的构建。

model = tf.keras.layers.Dense(units=1)  # 实例化线性层
plt.scatter(X, y)
plt.plot(X, model(X), c='r')

效果图如下：

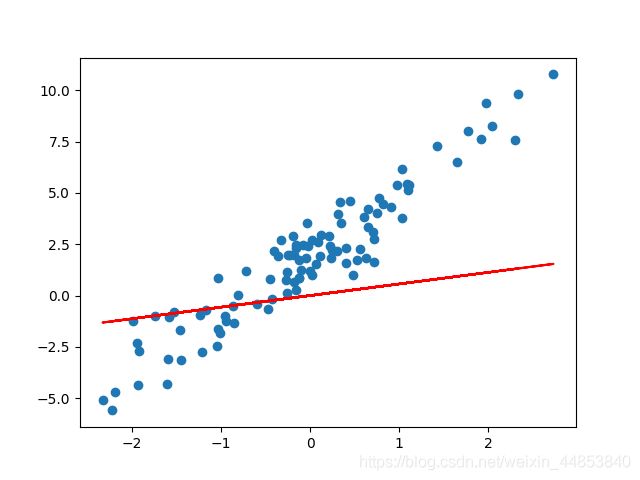
损失函数无需再自行构造，我们可以直接使用 TensorFlow 提供的平方损失函数 tf.keras.losses.mean_squared_error 计算，然后使用 tf.reduce_sum 求得全部样本的平均损失。

EPOCHS = 10
LEARNING_RATE = 0.002
for epoch in range(EPOCHS):  # 迭代次数
    with tf.GradientTape() as tape:  # 追踪梯度
        y_ = model(X)
        loss = tf.reduce_sum(tf.keras.losses.mean_squared_error(y, y_))  # 计算损失

    grads = tape.gradient(loss, model.variables)  # 计算梯度
    optimizer = tf.keras.optimizers.SGD(LEARNING_RATE)  # 随机梯度下降
    optimizer.apply_gradients(zip(grads, model.variables))  # 更新梯度
    
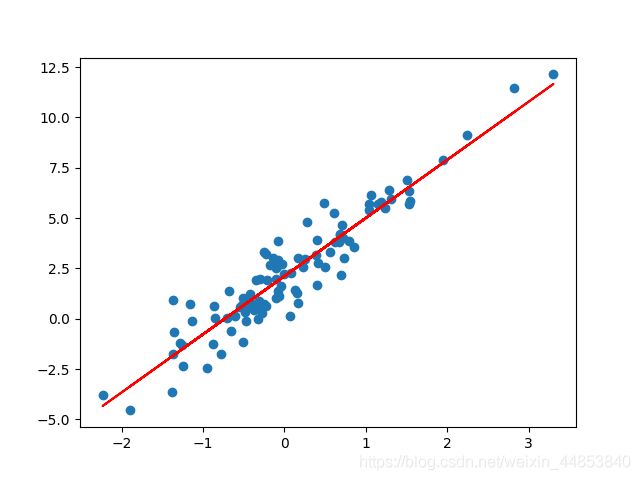
plt.scatter(X, y)
plt.plot(X, model(X), c='r')

效果图如下：

Keras实现

上面的高阶 API 实现过程实际上还不够精简，我们可以完全使用 TensorFlow Keras API 来实现线性回归。

model = tf.keras.Sequential()  # 新建顺序模型
model.add(tf.keras.layers.Dense(units=1, input_dim=1))  # 添加线性层
model.summary()  # 查看模型结构
model.compile(optimizer='sgd', loss='mse')  # 指定损失函数为 MSE 平方损失函数，优化器选择 SGD 随机梯度下降
model.fit(X, y, epochs=10, batch_size=32)  # 训练模型
plt.scatter(X, y)
plt.plot(X, model(X), c='r')

效果图如下：

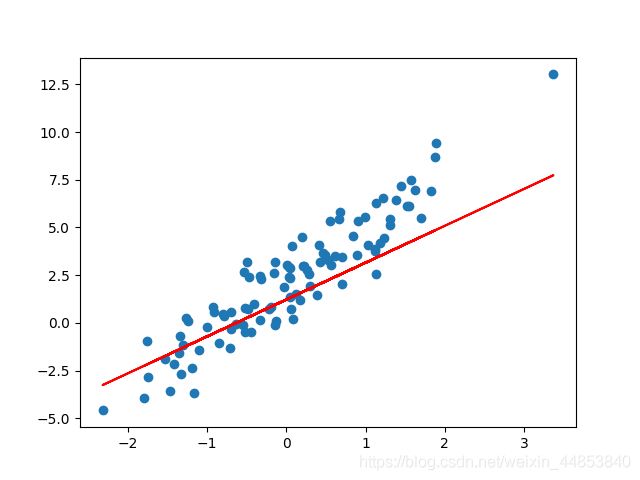
完全使用 Keras 高阶 API 实际上只需要 4 行核心代码即可完成，相比于最开始的低阶 API 简化了很多。

model = tf.keras.Sequential()  # 新建顺序模型
model.add(tf.keras.layers.Dense(units=1, input_dim=1))  # 添加线性层
model.compile(optimizer='sgd', loss='mse')  # 定义损失函数和优化方法
model.fit(X, y, epochs=10, batch_size=32)  # 训练模型