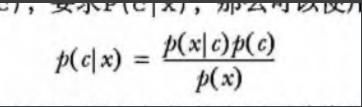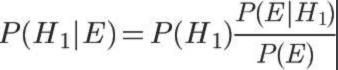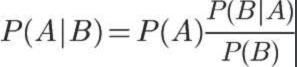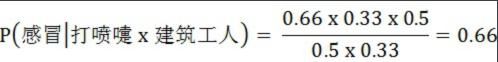贝叶斯分类器的matlab实现_教你学Python28-朴素贝叶斯简介
一、引子
最近几天一直没来得及看《机器学习实战》这本书,感觉停滞了很久,因为需要对 AIMI-CN的规划进行考虑,想了很久做了一些皮毛的东西,决定还是慢慢来按部就班,东西做出来才能说话,当然之后我做这个文章的时候,也尽量再多点自己的东西把,其他人写的多数当参考把,这样才会有更多自己原创的东西,大家才会看,才会认同把~
二、朴素贝叶斯理论
朴素贝叶斯是贝叶斯决策理论的一部分,所以在讲述朴素贝叶斯之前有必要快速了解一下贝叶斯决策理论。
1、贝叶斯决策理论
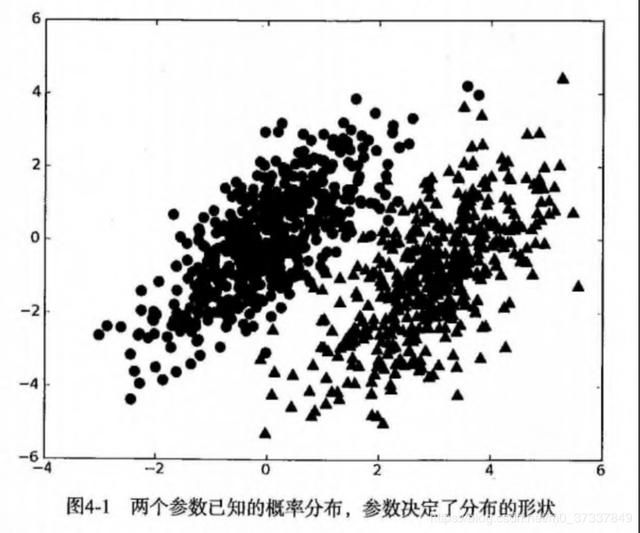
假设现在我们有一个数据集,他由两类数据组成,数据分布如下图所示:
我们现在用 p1(x,y) 表示数据点 (x,y) 属于类别 1(图中用圆点表示的类别)的概率,用 p2(x,y) 表示数据点 (x,y) 属于类别 2(图中三角形表示的类别)的概率,那么对于一个新数据点 (x,y),可以用下面的规则来判断它的类别:
- 如果 p1(x,y) > p2(x,y) ,那么类别为1
- 如果 p2(x,y) > p1(x,y) ,那么类别为2
也就是说,我们会选择高概率对应的类别。这就是贝叶斯决策理论的核心思想,即选择具有最高概率的决策。
2、条件概率
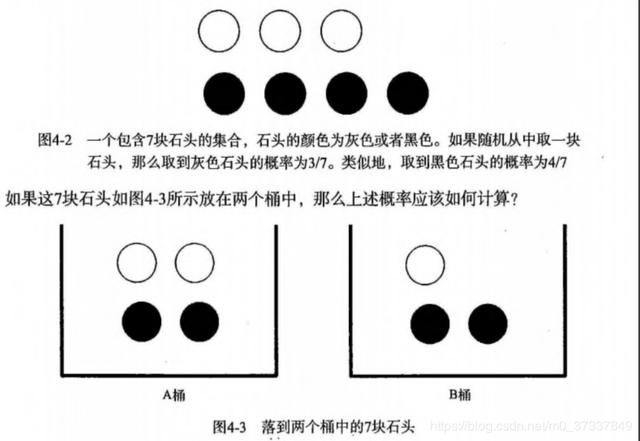
有一个装了 7 块石头的罐子,其中 3 块是白色的,4 块是黑色的。如果从罐子中随机取出一块石头,那么是白色石头的可能性是多少?由于取石头有 7 种可能,其中 3 种为白色,所以取出白色石头的概率为 3/7 。那么取到黑色石头的概率又是多少呢?很显然,是 4/7 。我们使用 P(white) 来表示取到白色石头的概率,其概率值可以通过白色石头数目除以总的石头数目来得到。
计算 P(white) 或者 P(black) ,如果事先我们知道石头所在桶的信息是会改变结果的。这就是所谓的条件概率(conditional probablity)。假定计算的是从 B 桶取到白色石头的概率,这个概率可以记作 P(white|bucketB) ,我们称之为“在已知石头出自 B 桶的条件下,取出白色石头的概率”。很容易得到,P(white|bucketA) 值为 2/4 ,P(white|bucketB) 的值为 1/3 。
条件概率的计算公式如下:
指在事件B发生的情况下,事件A发生的概率,用P(A|B)来表示。
P(white|bucketB) = P(white and bucketB) / P(bucketB)
首先,我们用 B 桶中白色石头的个数除以两个桶中总的石头数,得到 P(white and bucketB) = 1/7 .其次,由于 B 桶中有 3 块石头,而总石头数为 7 ,于是 P(bucketB) 就等于 3/7 。于是又 P(white|bucketB) = P(white and bucketB) / P(bucketB) = (1/7) / (3/7) = 1/3 。
另外一种有效计算条件概率的方法称为贝叶斯准则。贝叶斯准则告诉我们如何交换条件概率中的条件与结果,即如果已知 P(x|c),要求 P(c|x),那么可以使用下面的计算方法:
3、贝叶斯推断
上面最后那张图就是贝叶斯准则,根据这个公式,以及条件概率公式进行变形,可以得到如下形式:
事件B发生的情况下,事件A发生的概率,用P(A|B)来表示
我们把P(A)称为"先验概率"(Prior probability),即在B事件发生之前,我们对A事件概率的一个判断。
P(A|B)称为"后验概率"(Posterior probability),即在B事件发生之后,我们对A事件概率的重新评估。
P(B|A)/P(B)称为"可能性函数"(Likelyhood),这是一个调整因子,使得预估概率更接近真实概率。
所以,条件概率可以理解成下面的式子:
后验概率 = 先验概率 x 调整因子我们举一个加深贝叶斯推断的例子:来自这里
两个一模一样的碗,一号碗有30颗水果糖和10颗巧克力糖,二号碗有水果糖和巧克力糖各20颗。现在随机选择一个碗,从中摸出一颗糖,发现是水果糖。请问这颗水果糖来自一号碗的概率有多大?
我们假定,H1表示一号碗,H2表示二号碗。由于这两个碗是一样的,所以P(H1)=P(H2),也就是说,在取出水果糖之前,这两个碗被选中的概率相同。因此,P(H1)=0.5,我们把这个概率就叫做"先验概率",即没有做实验之前,来自一号碗的概率是0.5。
再假定,E表示水果糖,所以问题就变成了在已知E的情况下,来自一号碗的概率有多大,即求P(H1|E)。我们把这个概率叫做"后验概率",即在E事件发生之后,对P(H1)的修正。
根据条件概率公式,得到
已知,P(H1)等于0.5,P(E|H1)为一号碗中取出水果糖的概率,等于30÷(30+10)=0.75,那么求出P(E)就可以得到答案。根据全概率公式,
所以,
将数字代入原方程,得到
这表明,来自一号碗的概率是0.6。也就是说,取出水果糖之后,H1事件的可能性得到了增强。
同时再思考一个问题,在使用该算法的时候,如果不需要知道具体的类别概率,即不需要知道上面P(H1|E)=0.6,只需要知道所属类别,即只需要知道来自一号碗,我们有必要计算P(E)这个全概率吗?要知道我们只需要比较 P(H1|E)和P(H2|E)的大小,找到那个最大的概率就可以。既然如此,两者的分母都是相同的,那我们只需要比较分子即可。即比较P(E|H1)P(H1)和P(E|H2)P(H2)的大小,所以为了减少计算量,全概率公式在实际编程中可以不使用。
----------------------------------------------例子完----------------------------------------------
4、朴素贝叶斯推断
理解了贝叶斯推断,那么让我们继续看看朴素贝叶斯。贝叶斯和朴素贝叶斯的概念是不同的,区别就在于“朴素”二字,朴素贝叶斯对条件个概率分布做了条件独立性的假设。 我们假设特征之间 相互独立 。所谓 独立(independence) 指的是统计意义上的独立,即一个特征或者单词出现的可能性与它和其他单词相邻没有关系,比如说,“我们”中的“我”和“们”出现的概率与这两个字相邻没有任何关系。这个假设正是朴素贝叶斯分类器中 朴素(naive) 一词的含义。朴素贝叶斯分类器中的另一个假设是,每个特征同等重要。
比如下面的公式:
由于每个特征都是独立的,我们可以进一步拆分公式 :
这样我们就可以进行计算了。意思就是,事件X发生的情况下,事件A发生的概率,用P(a|X)来表示,此时的事件X里面有很多相对独立的特征,这时候就要把X事件的所有特征都分别提取出来进行计算
我们讲一个例子来进行对朴素贝叶斯进行剖析:
某个医院早上来了六个门诊的病人,他们的情况如下表所示:
现在又来了第七个病人,是一个打喷嚏的建筑工人。请问他患上感冒的概率有多大?
根据贝叶斯定理:
可得:
根据朴素贝叶斯条件独立性的假设可知,"打喷嚏"和"建筑工人"这两个特征是独立的,因此,上面的等式就变成了
这里可以计算:
因此,这个打喷嚏的建筑工人,有66%的概率是得了感冒。同理,可以计算这个病人患上过敏或脑震荡的概率。比较这几个概率,就可以知道他最可能得什么病。
这就是贝叶斯分类器的基本方法:在统计资料的基础上,依据某些特征,计算各个类别的概率,从而实现分类。
同样根据上面那个糖果例子的最后说明,在编程的时候,如果不需要求出所属类别的具体概率,P(打喷嚏) = 0.5和P(建筑工人) = 0.33的概率是可以不用求的。
三、朴素贝叶斯开发流程
1、朴素贝叶斯 工作原理
提取所有文档中的词条并进行去重获取文档的所有类别计算每个类别中的文档数目对每篇训练文档: 对每个类别: 如果词条出现在文档中-->增加该词条的计数值(for循环或者矩阵相加) 增加所有词条的计数值(此类别下词条总数)对每个类别: 对每个词条: 将该词条的数目除以总词条数目得到的条件概率(P(词条|类别))返回该文档属于每个类别的条件概率(P(类别|文档的所有词条))2、朴素贝叶斯 开发流程
收集数据: 可以使用任何方法。准备数据: 需要数值型或者布尔型数据。分析数据: 有大量特征时,绘制特征作用不大,此时使用直方图效果更好。训练算法: 计算不同的独立特征的条件概率。测试算法: 计算错误率。使用算法: 一个常见的朴素贝叶斯应用是文档分类。可以在任意的分类场景中使用朴素贝叶斯分类器,不一定非要是文本。3、朴素贝叶斯 算法特点
优点: 在数据较少的情况下仍然有效,可以处理多类别问题。缺点: 对于输入数据的准备方式较为敏感。适用数据类型: 标称型数据。结语:这节主要说了贝叶斯和朴素贝叶斯的基本原理和区别,下节我们就针对具体问题进行项目实战。
喜欢点下关注,你的关注是我写作的最大支持